无人机滑降着陆控制系统设计

范东生，孙恒义，麻兴斌，牛振中

(西安爱生技术集团公司，西安 710129)

0 引言

由于无人机具有造价低、安全性高、实用性强等优点，在军用和民用领域都扮演着越来越重要的作用。对于固定翼无人机而言，起降成为了制约其发展的主要因素，目前常用的固定翼无人机回收方式包括起落架跑道滑降、滑橇滑行，伞降以及垂直起降[1]。伞降是当无人机到达降落区域上空后自动或手动控制打开降落伞完成后续伞降着陆；垂直起降主要针对旋翼无人机或倾转旋翼无人机的降落，对滑降阶段的三维航迹跟踪要求不高。针对滑橇滑行以及起落架滑行两种回收方式，对自主着陆下滑飞行的平稳性、横侧向纠偏的高效性、降落位置的准确性以及落地姿态角的安全性提出了严格的要求。

高九州[2]以无人机地速、下沉率和横侧向偏航距为控制目标，应用内模控制原理，完成了着陆纵向和横向滑降控制器的设计，其在末端拉起时采用了高度的指数衰减控制，通过高度的控制将无人机姿态摆平，这种策略存在姿态响应、收敛慢的缺点，可能会导致落地姿态角差无人机受损。朱雯雯[3]将着陆阶段分为直线下滑和指数拉起以及浅下滑来设计，并选择不同的空速和轨迹角下飞机模型的配平结果作为滑降的依据，能满足无人机滑降段对飞行高度和侧向偏差的要求，但整个过程采用速度开环控制，无人机空速在下滑段变化较大，实际飞行数据无法与配平值中的姿态很好地对应。

针对以上分析，本文首先设计了无人机滑降着陆控制系统结构图，具体设计了滑降横侧向控制器和滑降纵向控制器，并在横侧向控制器设计中给出了直线航迹和圆航迹的控制律设计方法，在纵向控制器设计中进行了下滑段高度控制量的分析计算；然后设计了一种滑降着陆控制系统，详细介绍了滑降过程控制模式，最后通过仿真实验完成对该滑降控制系统进行验证。

1 滑降着陆控制系统结构设计

无人机滑降着陆控制包括滑降横、侧向控制和滑降纵向控制[5]。航迹控制结构如图1所示，其中包括飞机模型、执行机构、飞行控制系统(包括横侧向控制器和纵向控制器)、传感器模块和导航系统(包括航线角、偏航距以及高度控制量的计算)。

图1 无人机滑降控制系统结构图

1.1 滑降横侧向控制器设计

在无人机进入滑降阶段后，要保证无人机尽快地跟踪上预定的航线，减小横向偏移能使无人机顺利通过下滑窗口，且在拉平段末端要减小与预定跑道的偏差，这就需要进行横侧向的精确控制。横侧向控制器是以航向角控制为内回路，航向角控制器的输出量作为副翼和方向舵执行机构的控制量，通过调节副翼和方向舵实现无人机的平面航迹控制。当无人机与预定航迹出现偏差时，需要对其进行纠偏控制，而航向角的控制量也是由航线角与航迹偏差的控制综合后得出，具体的滑降横侧向控制结构如图2所示。

图2 滑降横侧向控制结构图

实现过程为：由无人机的位置和给定的航程点，计算出无人机与航线的垂线距离以及航线角，通过航迹控制器来消除偏差，并得到所需的航向角控制量，将其给入到航向控制器中，通过执行结构不断调整副翼和方向舵的偏转角度，从而实现无人机对平面航迹的跟踪。

在滑降过程中会用到航线跟踪以及定点圆盘旋降高。对直线航迹而言，偏航距离通过无人机到当前航线的距离计算，具体的航向角控制率如下：

(1)

圆航迹的偏航距离通过无人机到圆心的距离与盘旋半径的差来得到，具体的航向角控制率如下:

(2)

式(1)中，ψ0为航线航迹角，Δd为偏航距，KP为比例系数，KI为积分系数，KD为微分系数，式(2)中，V为无人机的飞行速度，R为圆盘旋半径。

1.2 滑降纵向控制器设计

滑降过程中不仅对无人机的平面航迹偏差有较高要求，而且无人机的高度控制以及触地时的俯仰角也要满足一定条件。所以在滑降过程中不仅要对无人机的高度进行跟踪控制，同时也要在接近地面时对无人机的俯仰角进行拉起控制，以确保触地时飞机抬头，起落架后轮先触地。无人机的高度控制以俯仰角控制回路为内回路，俯仰角控制器的输出量作为升降舵执行机构的控制量，通过调节升降舵实现无人机的高度控制[6-7]。其中，高度控制量的计算是通过导航系统解算完成的。具体的高度控制器结构如图3所示。

图3 滑降纵向控制器结构图

实现过程为：首先，根据地面站发送的滑降航线的航程点，导航软件将航程点的高度信息提取后，根据无人机当前的位置，通过数学方法实时计算无人机所需的高度控制量，将其送入到飞控系统的高度控制器中，通过调节升降舵的偏转角来实现无人机的高度控制[8]。当飞机距离地面高度较低时，采用内环俯仰角控制，将飞机纵向姿态拉平，以免发生飞机机头或螺旋桨先触地的情况。

高度控制量的计算方法：通过给点的航程点坐标，实时计算无人机在任意航线位置时对应的应飞高度值，具体的计算过程如下[4]：

如图4所示，AB表示当前无人机的航线，其中航程点A(xA,yA,zA)和B(xB,yB,zB)的位置已知，将AB投影到水平面XOY上得到线段CD，其中C的坐标为(xC,yC,0)，D的坐标为，且有xA=xC，yA=yC，xB=xD，yB=yD。

图4 投影法计算高度

坐标点E表示无人机的位置，为了求出无人机在E点时对应的航线应飞高度，将E投影到水平面得到点F，再将F点投影到上CD，得到投影点G，而G点对应的AB航线上的H点的高度值即为无人机的应飞高度。

在图4中，E(xE,yE,zE)点的坐标已知，则F(xE,yE,0)已知，又因为直线AB已知，则GF的数学式：

(3)

直线CD的表达式为：

(4)

设G点坐标为G(xG,yG,0)，联合式(3)和式(4)，可得:

xG=

(5)

yG=

(6)

为了方便计算，将平面ABCD分离出来，如图5所示。由上述计算求得G点坐标为G(xG,yG,0)，且A、B、C、D的坐标均已知，当航程点A的高度坐标值低于B点高度坐标值时，见图5左图。

图5 航线侧面投影

根据几何知识可以推导出如下关系：

(7)

则可以推导出H点的高度值，即无人机的应飞高度h为：

(8)

同理，当航程点A的高度坐标值高于B点高度坐标值时，见图5右图，可以推导出H点高度值h为：

(9)

通过上述方法，可以求得无人机在任意位置时对应的应飞高度，即无人机的高度控制量，通过高度控制器实现对航线高度的跟踪控制。

2 滑降着陆控制模式

根据滑降着陆过程中对飞机航迹和姿态的要求，将滑降过程分为4个阶段[9]，分别为盘旋降高段、平飞段、下滑段以及末端拉平段。从平飞段到无人机着陆的滑降过程如图6所示。

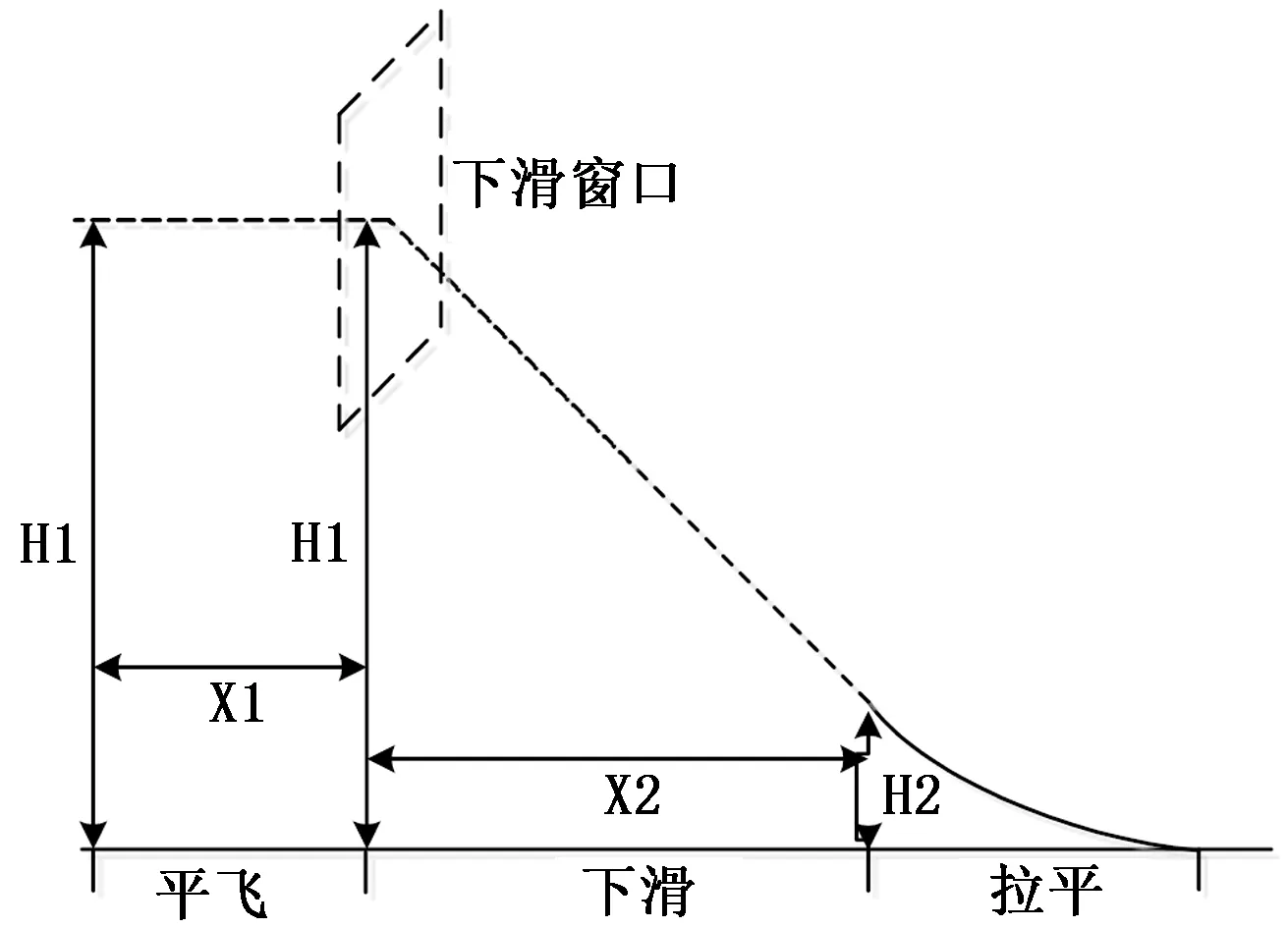
图6 滑降过程图

滑降过程首先是降高段，当无人机返回到降落点上空后先进行圆盘旋降高，此时采用速度闭环方式，发动机工作在慢车状态，当高度满足一定条件且飞机航向角与滑降下滑线的航线角之间满足设置的条件后便开始进入水平平飞段；平飞段是保证飞机很好的跟踪水平航迹，减小飞机的侧向偏移，并进行下滑前姿态调整；平飞段末端进行飞机下滑窗口判断，当满足下滑窗口约束后进入到下滑段；下滑段控制无人机始终跟踪给定的航线坡度，同样在下滑段采用速度闭环控制方式，发动机工作在慢车状态，直到高度满足一定条件后进入拉平段[10]，在拉平段发动机怠速运行，纵向控制模式由高度控制切换为俯仰角控制，完成触地前俯仰角调整。

1) 由降高段进入平飞段的判断条件为：

(1)无人机飞行高度<=H1；

(2)飞机航向角与航线的夹角小于10度或者飞机距离圆盘旋与航线切点位置距离小于50 m。

2)平飞段高度H1设置为200 m，平飞段水平距离X1设置为3 000 m。为了使无人机从圆盘旋进入直线航线后有较长时间收敛，X1的值可以根据地形条件考虑适当放大。

3) 下滑窗口判断条件：

(1)无人机沿航线方向飞行，与下滑航线起点距离小于50 m；

(2)飞机的偏航距离绝对值小于10 m；

(3)飞机当前高度与平飞段高度给定值的差的绝对值小于10 m。

4)预定下滑点到拉平点的水平距离X2设置为4 000 m，拉平高度H2为10 m，第一次下滑到预定拉平高度后开始进入拉平段。

5)进入拉平段后，发动机风门减小，设置为怠速运行状态。

6)拉平段采用俯仰角控制，具体的俯仰角给定值计算方法为：

(10)

其中：H3为飞机相对跑道的高度；H2为预定拉平高度；θ0为拉平段初始俯仰角给定值，取下滑段转换到拉平段时的俯仰角指令值；θ1为接地俯仰角指令给定值，为了保证接地时后轮先触地且螺旋桨不会划到地面，降其设置为2°。

3 仿真与分析

根据前边对滑降模型的分析，给定滑降航线为：(0,0,1 000)，(7 000,0,200)，(10 000,0,200)，(14 000,0,10)， (15 000,0,0)。初始时间为0 s，无人机初始飞行高度为1 000 m，空速为40 m/s，航向角为0°，发动机工作时的最小风门开度限制为10%。无人机从初始状态进入航线，完成滑降过程，具体的仿真结果如图7～11所示。

图7 无人机滑降平面图

图8 无人机滑降x-h图

图9 无人机滑降空速图

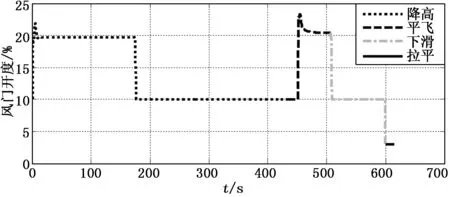
图10 无人机滑降风门开度图

图11 无人机滑降俯仰角图

无人机从初始位置出发，沿着x轴方向飞行，当到达7 000 m位置处开始进行切航线圆盘旋降高飞行。由图7～11可知，盘旋降高阶段圆盘旋半径为1 000 m，俯仰角为-6°，由于给定速度为40 m/s，而下滑时无人机的势能转化为动能，飞行速度增大到50 m/s。节气门开度保持最小值10%。整个盘旋降高过程用时约260 s，高度从1 000 m下降至200 m，下滑率为3.08 m/s。

当无人机飞行高度不大于200 m时，无人机航向角与航线的夹角小于10度或飞机距离圆盘与航线之间切点的距离小于50 m时，无人机进入平飞段。由图7～11可知，刚从圆盘旋进入平飞段时，会出现最大45 m的偏航距，平飞段沿着x方向飞行3 000 m，平飞段结束时，航迹偏差收敛到5 m。飞行高度保持200 m，对应的俯仰角约为0度。无人机空速从下滑段末端的50 m/s，通过速度的闭环调节控制，保持到给定值40 m/s，对应的发动机风门开度约为21%。

平飞段结束后进入下滑窗口判断，由于此时侧向偏航距为5 m，飞行高度为200 m，高度控制误差为0 m，满足窗口通过条件，即当无人机与下滑航线起点距离小于50 m时，直接进入下滑阶段。由图5～9可知，下滑阶段无人机的偏航距逐渐减小，当下滑段结束时，偏航距为0 m。由于下滑段高度控制为实时计算无人机当前位置对应的下滑高度，而高度控制到该值需要一定的时间，所以不能保证无人机完全跟踪下滑航线，而是在航线上方以相同的坡度下滑，同一水平位置下，无人机的应飞高度与实际飞行高度偏差约为2 m。整个下滑过程用时约90 s，下滑高度为190 m，高度下滑率为2.11，下滑率较盘旋降高时减小，俯仰角约为-4°，空速增长幅度小于盘旋降高阶段，最高达到44 m/s，由于采用速度闭环控制，对应的发动机风门开度逐渐减小至10%。

当无人机下滑到距离地面高度小于10 m时，进入到拉平阶段，发动机怠速运转。由图7～11可知，无人机从10 m高度到触地用时14 s，高度下滑率为0.71m/s。发动机怠速运行后，无人机速度从43 m/s降低至37 m/s，水平方向无人机从14 040 m位置处滑行到14 650 m，共滑行610 m。触地时的俯仰角为0.4°，飞机保持较小的抬头姿态角，满足滑降着陆对无人机的触地俯仰角要求。

4 结束语

本文通过分析当前无人机的滑降着陆控制方式，结合某型无人机模型，设计了一种无人机滑降着陆控制方式，首先进行了滑降着陆控制系统架构设计，给出了滑降横侧向控制器结构，并在横侧向控制器设计中进行了直线航迹和圆航迹的控制律设计；之后设计了滑降纵向控制器结构，在纵向控制器设计中给出了下滑段高度控制量的计算方式；在滑降着陆控制结构的基础上，设计了一种滑降着陆控制流程，详细介绍了滑降过程的控制模式。

经过仿真分析表明：1)无人机在整个滑降过程中横向控制满足设计要求。在刚进入平飞段时由于航线切换出现45 m偏航，在平飞段结束时偏航距为5 m，在飞机接地时，偏航距减小为0 m。2)整个过程中高度控制和接地俯仰角满足设计要求。平飞段飞机飞行高度为200 m，控制误差为0 m；下滑段高度跟踪误差为2 m；接地时无人机姿态为稍微抬头，俯仰角为0.4°。

本文设计的无人机滑降着陆控制系统能很好地完成回收阶段无人机的安全着陆，整个滑降过程中具有偏航距离小，高度控制误差低，水平方向滑行距离较短，落地姿态角安全性高的优点，能满足滑跑型无人机对滑降阶段的控制要求。