一种基于自适应网格机制的强机动目标滤波算法

何金刚 徐林峰 张金鹏 余治民

摘 要：本文以提升空空导弹在空战中的对抗能力为背景， 开展针对强机动目标的滤波算法设计， 以提高目标跟踪精度。 首先， 对强机动目标滤波算法开展分析， 提出以交互式多模型算法为基础的混合网格多模型（HGMM）算法。 其次， 针对混合网格多模型算法开展详细设计。 最后， 通过数字仿真验证了该算法可行且跟踪效果良好， 跟踪精度提高了约20%。

关键词：     自适应网格; 交互多模型; 混合网格多模型; 机动目标; 目标跟踪; 滤波算法; 空空导弹

中图分类号：     TJ760; V212.13+5 文献标识码：    A 文章编号：     1673-5048（2021）06-0040-06

0 引  言

随着新型推力矢量涡扇发动机、 先进气动设计、 双向数据链和隐身技术的应用， 第四代战斗机和无人作战飞机等新一代航空武器相继出现， 使得空空导弹在未来战争中将面临机动能力更强、 逃逸方式更复杂、 可探测性更差的攻击目标[1]。 当前， 周边国家和地区已经大量装备或在研具有大机动能力（过载9左右）的第三代和第四代战斗机， 已经预先研究且未来可能装备更高机动能力（过载12～20）的无人战斗机以及机动能力达到3g左右、 飞行马赫数大于5的临近空间高超声速无人飞行器。 因此， 空空导弹制导技术必须满足未来抗强机动目标的能力需求。 对空战目标信息的快速准确估计是实现空空导弹精确攻击的前提， 直接决定着制导的精度和攻击的成功率[1-3]。 本文以空空导弹对抗强机动目标为需求， 对滤波算法进行设计， 以提高对机动目标的信息估计性能。

1 强机动目标滤波算法分析

在雷达型导弹制导系统中导引头测量值无法直接使用， 需使用滤波算法对其信息进行处理， 得到目标状态估计值以供制导律使用。 大机动目标跟踪涉及到目标运动建模和基于模型的最优估计， 两者相互耦合[4-5]： 估计误差会引起辨识风险， 辨识错误又将降低估计精度。 只有联合优化状态估计与参数辨识， 才能提高跟踪的稳定性和精确性[6]。 多模型方法是一种联合估计与辨识处理策略， 也是目前解决机动目标跟踪问题的主流方法， 其研究重点在模型辨识上。 这种概率匹配下的多模型跟踪算法通常具有鲁棒性好和并行处理能力[7]。

交互多模型（IMM）算法是目前混合估计算法研究的主流， 具有明显的并行结构， 便于有效地并行实现。 交互多模型结合多个假定的目标运动模型， 如匀速（CV）、 匀加速（CA）、 常速转弯（CT）、 变速转弯、 Singer模型、 “当前”统计模型[8-10]。 对于单个目标， IMM需要根据结合的模型数量设置相应数量的滤波器， 并通过先验知识设定服从马尔科夫链的模型转移概率矩阵。 在跟踪滤波开始后， 根据接收到的量测信息， 通过一定的逻辑计算其在各个模型下与目标真实运动模式的贴合程度， 更新模型概率， 以此计算出本时刻关于目标状态的最优估计值， 完成自适应。 IMM算法状态估计精度极大程度上依赖于模型集的设计， 即设计的模型集与目标真实运动的贴合程度。 可以说， IMM算法如果覆盖目标可能进行的所有运动模式， 需要的模型数量非常庞大而导致无法实现滤波器的实时跟踪。

对于未知的机动类型及其参数， 如果离散量化建立典型目标运动模型集合，  则模型个数随参数维度呈指数级增长， 不适用于高机动目标的实时处理跟踪。 另一方面， 如果用有限少量的运动模型去刻画高机动运动模式， 尽管可以满足估计器计算实时性要求， 但很难完备覆盖千变万化的目标运动形式， 从而造成运动模型不同程度的失配和估计上的大误差， 尤其会造成加速度这一制导核心参数的较大估计误差。

混合网格多模型（HGMM）算法是在IMM的基础上发展起来的， 能够基于量测数据和历史模板， 融合生成能准确描述高机动特性的精细化运动模型集， 有效克服高機动引起的模型失配问题[11]。 因此， HGMM这种变结构多模型算法通过一定的规则自行改变模型集中的模型， 使模型集在每个时刻更贴近真实的目标运动状态， 即达到以小的模型集覆盖所有可能的运动模式。 另外， HGMM在与IMM具有相同精度的情况下计算量要小得多。

2 HGMM算法设计

2.1 算法框架设计

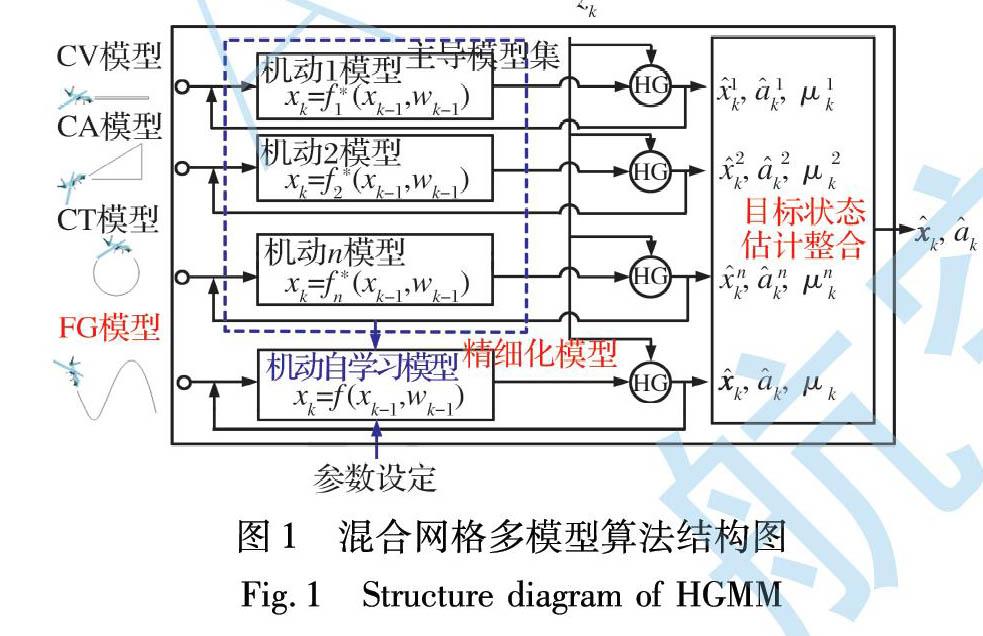
HGMM为基于混合网格多模型的卡尔曼滤波算法， 本质上是一种模型自学习算法。 其输入、 输出如图1所示。 主导模型集为预先设定好的一些模型的集合， 包含如CV模型、 CA模型、 CT模型等， 在整个跟踪滤波过程中保持不变。 根据模型， 可由目标上一时刻的状态得出目标本时刻的状态。 精细化模型集为算法在每次跟踪滤波过程中通过模型自学习机制学习到的模型的集合， 包含如FG模型等。 zk为当前时刻接收到的量测， 将其与每个模型进行结合（包含主导模型集中的模型和精细化模型集中的模型）， 根据一定的算法， 得到每个模型单独作用时的估计值， 即x^jk， a^jk， μjk。 最后， 综合各x^jk， a^jk， μjk， 根据目标状态估计融合准则， 得到当前时刻总的目标状态估计值x^k和总的加速度扰动量估计值a^k。 在k+1时刻， 将各个模型的x^jk， a^jk， μjk作为初始值进行滤波估计。

HGMM通过模型集参数设置。 首先， 选定固定个数的主导模型， 构成粗网格。 其次， 在每次滤波估计中， 基于模型概率， 计算出单个或数个精细化的期望模型， 构成自适应的细网格。 最终， 细网格与粗网格结合共同进行滤波估计。 需要注意的是， 精细化的期望模型集仅在当次滤波估计中起作用， 其在概率统计意义上相比于固定模型集更贴近目标真实运动状态。

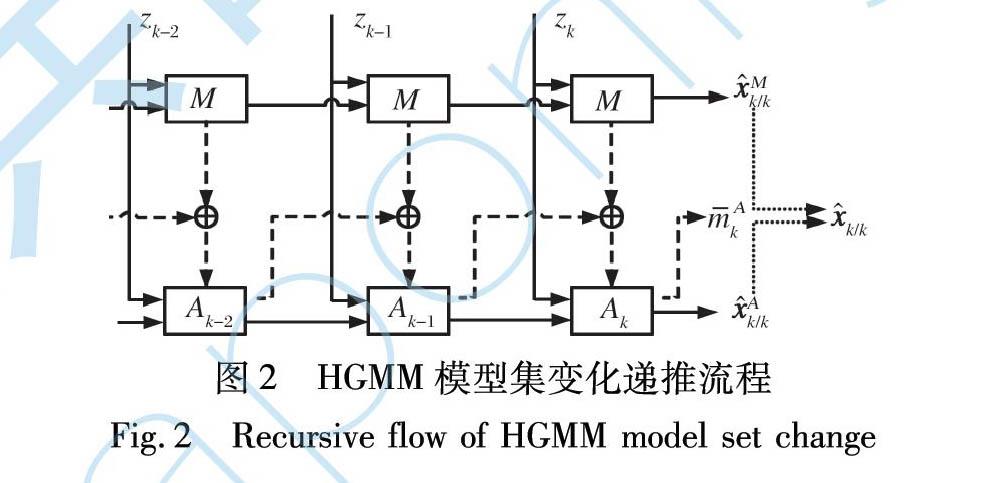
在此给出HGMM算法的递推逻辑。 以M表示固定的模型集（粗网格）， Ak表示自适应的模型集（细网格）， 则k时刻的总模型集可以表示为Mk=M∪Ak。 算法中， 有如下的总模型集中模型的递推关系：

Mk-1=M∪Ak-1→Mk=M∪Ak （1）

即粗网格在所有时刻都保持不变， 而细网格则不断变化， 以此实现小的模型集覆盖大的模式空间。 模型集变化的递推流程如图2所示。

可见， k时刻的自适应模型集（细网格）是由k-1时刻的自适应模型集与全程的固定模型集（粗网格）交互作用产生的。 另外， 每个采样时刻关于目标状态的最优估计值是由粗网格单独作用产生的状态估计值和细网格单独作用产生的状态估计值相融合得到的。

2.2 模型集设计

考虑如下非线性形式的随机混合系统：

xk+1=fk（M（i）， xk）+Γk（M（i））w（M（i））

zk=hk（M（i）， xk）+vk（M（i）） （2）

式中： M（i）为系统模型空间上的模式变量; fk（M（i）， xk）为状态转移函数; Γk（M（i））为过程噪声协方差阵; hk（M（i）， xk）为量测函数; wk和vk分别为过程噪声和量测噪声。

IMM算法设计基础在于模型集的选择。 在导弹打击目标的过程中， 目标的机动大多数是在进行匀加速运动或者转弯运动。 本文中的模型集包括匀加速运动模型和匀速转弯模型。

（1）匀速运动模型

定义状态向量：

X（k）=[x（k）， x·（k），  x¨（k）， y（k）， y·（k）， y¨（k）， z（k）， z·（k）， z¨（k）]T， 则状态方程可以表示为

X（k+1）=FX（k）+w（k）（3）

式中：

F=ΦΦΦ， Φ=1T0010000;

w（k）为高斯零均值白噪声， 方差为σ21。

（2）匀加速运动模型

定义状态向量：

X（k）=[x（k）， x·（k）， x¨（k）， y（k）， y·（k）， y¨（k）， z（k）， z·（k）， z¨（k）]T， 则状态方程可以表示为

X（k+1）=FX（k）+w（k）（4）

式中：

F=ΦΦΦ，Φ=1TT2201T001;

w（k）为高斯零均值白噪声， 方差为σ22。

（3）匀速（协同）转弯模型

定义状态向量：

X（k）=[x（k）， x·（k）， x¨（k）， y（k）， y·（k）， y¨（k）， z（k）， z·（k）， z¨（k）]T

， 则状态方程为

X（k+1）=FX（k）+w（k）（5）

式中：

F=ΦΦΦ， Φ=1sin（ωT）ω1-cos（ωT）ω20cos（ωT）sin（ωT）ω0-ωsin（ωT）cos（ωT）;

ω為转弯角速度; w（k）为高斯零均值白噪声， 方差为σ23。

此模型对应的过程噪声协方差矩阵Q为

Q=diag [Sxq， Syq， Szq]

q=6（ωT）-8sin（ωT）+sin2（ωT）4ω52sin4（ωT/2）ω4-2（ωT）+4sin（ωT）-sin2（ωT）4ω3

2sin4（（ωT）/2）ω42（ωT）-sin2（ωT）4ω3sin2（ωT）2ω2

-2（ωT）+4sin（ωT）-sin2（ωT）4ω3sin2（ωT）2ω22（ωT）+sin2（ωT）4ω

式中： Sx， Sy， Sz分别为过程噪声对应于各坐标轴的功率谱密度。

2.3 IMM算法

IMM的具体算法流程包括输入交互、 各滤波器滤波、 模型概率更新、 总体估计融合四个模块。

（1）输入交互

将前一采样时刻各滤波器（对应于IMM中单独的模型）的目标状态估计值作为输入， 同时根据服从马尔科夫链的模型转移概率、 前一时刻的模型概率计算混合概率。 以此为出发点， 计算出交互后对应于各个滤波器的目标状态值输入及其协方差。

设k-1时刻对应于各滤波器的目标状态估计值和目标状态估计协方差为xjk-1k-1和Pjk-1k-1（j=1， 2， …， N）， N为模型数量。

模型混合概率为

μijk-1∣k-1=pijμik-1cj （6）

式中： μik-1为前一时刻的模型概率; μijk-1k-1为当转移后模型为j时， 转移前模型为i的概率， i=1， 2， …， N。

一般根据先验信息人为设定的、 服从马尔科夫链的模型转移概率矩阵p为

p=p11…p1NpN1…pNN（7）

式中： pij为模型i转移到模型j的概率。

归一化常数cj为

cj=∑Ni=1pijμik-1（8）

模型混合概率计算后， 即可对前一采样时刻各滤波器的目标状态估计值和目标状态估计协方差进行交互， 并将交互后的值作为本采样时刻各滤波器的初始输入：

x^0jk-1∣k-1=∑Ni=1x^ik-1∣k-1μijk-1∣k-1（9）

P0jk-1∣k-1=∑Ni=1μijk-1∣k-1{Pik-1∣k-1+[x^ik-1∣k-1-

x^0jk-1∣k-1][x^ik-1∣k-1-x^0jk-1 k-1]T} （10）

（2）滤波过程

对应于各个滤波器， 根据自身模型的状态转移矩阵Fjk-1和过程噪声协方差矩阵Qjk-1等， 以各滤波器交互后的输入（式（9）～（10））为初值， 进行卡尔曼滤波。 计算出各个滤波器的目标状态估计值x^jkk及目标状态估计值的协方差Pjkk， 用于本采样时刻最后的总体估计融合， 以及下一时刻的输入交互。

（3）模型概率更新

计算当前时刻目标状态与当前各模型的匹配程度， 采用极大似然函数法， 更新模型概率矩阵中各模型所占的权重， 为下一时刻输入交互提供先决条件， 并且完成滤波估计过程中模型概率的自适应， 提高估计精度。

建立以预测点为中心、 新息协方差矩阵为方差的正态分布， 未知量为量测值。 假设量测值在空间中服从此分布， 则可以计算k时刻模型j与目标真实运动模型的匹配程度， 其极大似然函数为

Λjk=exp-12（vjk）T（Sjk）-1vjk2πSjk（11）

式中： vjk为对应于模型j的新息; Sjk为对应于模型j的新息协方差。

则更新后的模型概率为

μjk=Λjk∑Ni=1pijμik-1c （12）

归一化常数c为

c=∑Nj=1Λjkcj（13）

（4）总体估计融合

结合各个滤波器单独作用得出的估计值、 估计误差协方差， 以及更新后的模型概率， 进行信息（数据）融合， 得到总体的目标状态估计及其对应的协方差， 进行输出。

总体的目标状态估计值为

x^k∣k=∑Nj=1μjkx^jk∣k（14）

总体的状态估计协方差为

Pk∣k=∑Nj=1μjk{Pjk∣k+[x^jk∣k-x^k∣k][x^jk∣k-x^k∣k]T} （15）

2.4 HGMM算法

以IMM（·）表示2.3节IMM算法。  下面具体阐述HGMM算法流程。

定义粗网格中共有nM个固定模型， 则可得到粗网格下的滤波估计结果及其协方差：

[x^Mk|k， PMk|k]=IMM（{x^jk|k， Pjk|k， μj|Mk}nMj=1）（16）

式中： j为粗网格中单个固定模型; x^Mkk和PMkk为k时刻对应于固定模型集（粗网格）的状态估计及其协方差。

在此过程中， 可得到粗网格中对应于各个模型的新的模型概率μj|Mk和粗网格总的归一化常数c1：

μj∣Mk=μjk∣k-1Λjkc1（17）

c1=∑jμjk∣k-1Λjk（18）

式中： μjMk 为粗网格固定模型集M中单个模型j的概率， （j=1， 2， …， nM）; Λjk的计算同式（11）。

定义细网格中共有nA个自适应模型， 待设计的模型可表示为A={μr∣A， m（r）}nAr=1。 采用矩匹配设计细模型集A， 待设计的模型m（r）有均值m（r）和协方差Σ（r）， 矩匹配准则为

m=∑nAr=1μr|Am（r）（19）

Σ=∑nAr=1μr|A[Σ（r）+（m-m（r））（m-m（r））T] （20）

式中： μr|A（r=1， …， nA）为权重。 以上矩匹配考虑了设计模型的协方差， 从本质上消除了低概率的模型， 增加了高概率模型， 这与粒子滤波器重采样思路类似。

则可得到k时刻细网格下的滤波估计结果及其协方差：

[x^Ak∣k， PAk∣k]=IMM（{x^rk∣k， Prk-1∣k-1， μr∣Ak-1}nAr=1） （21）

式中： r为细网格中单个自适应模型。

在此过程中， 可得到细网格中对应于各个模型的新的模型概率μr∣Ak和细网格总的归一化常数c2：

μr∣Ak=μrk∣k-1Λrkc2（22）

c2=∑rμrk∣k-1Λrk（23）

式中：  μrAk 为细网格自适应模型集A中单个模型r的概率（r=1， 2， …， nA）; Λrk的计算同式（11）。

经过上述计算后， 可得粗网格的总的模型概率和细网格的总的模型概率：

μMk=c1c1+c2（24）

μAk=1-μMk（25）

HGMM算法总的状态估计及其协方差可以表示为

x^k∣k=x^Mk∣kμMk+x^Ak∣kμAk （26）

3 仿真分析

针对HGMM算法设计， 构建典型机动场景进行了数字仿真验证。

雷达量测包括径向距r和角度θ， 测量精度（即标准差）分别为10 m和0.03°。 考虑在笛卡尔坐标系下滤波， 转换到直角坐标量测轴方向和轴方向标准差均为15 m。 采样周期0.1 s。 对于已知场景下的目标跟踪， 可直接根据运动模型和量测实现状态估计。 也就是对于此场景， 如果精确知道其运动模式， 可以利用匀速转弯运动模型结合卡尔曼滤波器实现最优估计。 现实问题是， 机动目标的运动形式多种多样， 無法预先判定。 机动目标跟踪的关键问题是运动模式的不确定性， 因此， 本文采用统一的匀速运动模型检验各算法的优劣。

本仿真对IMM与HGMM两种算法进行测试和比较。 其中匀速运动模型的已知输入模型集包括：

u=10g·010-101-1-110010-111-1-1 （27）

式中的模型集包括九种运动模型。 第一列代表在x， y轴加速度均为0; 第二列代表在x， y轴加速度分别为10g与0， 后续各列物理含义相同。 第一列表示匀速运动模型， 其余八列子模型均为各轴分别为匀加速运动的合成。

场景1：

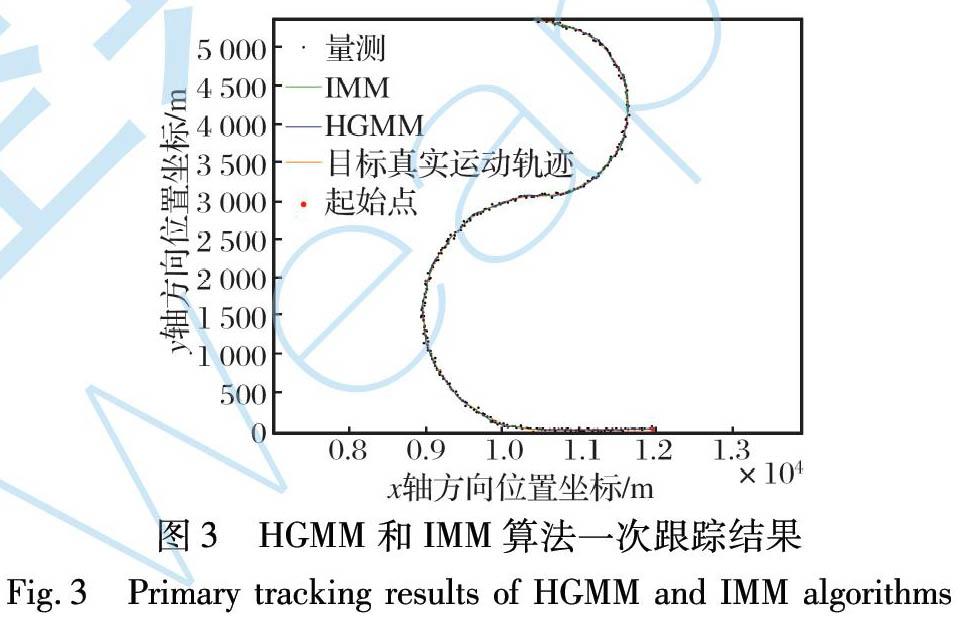
初始状态x0=[12 000 m， -300 m/s， 0 m， 0 m/s]T， 前5 s匀速运动， 之后做半个圆周的-6g转弯（逆时针为正， 以下转弯加速度定义相同）， 再做半个圆周的8g转弯。 其轨迹以及两种算法的一次跟踪结果如图3所示。

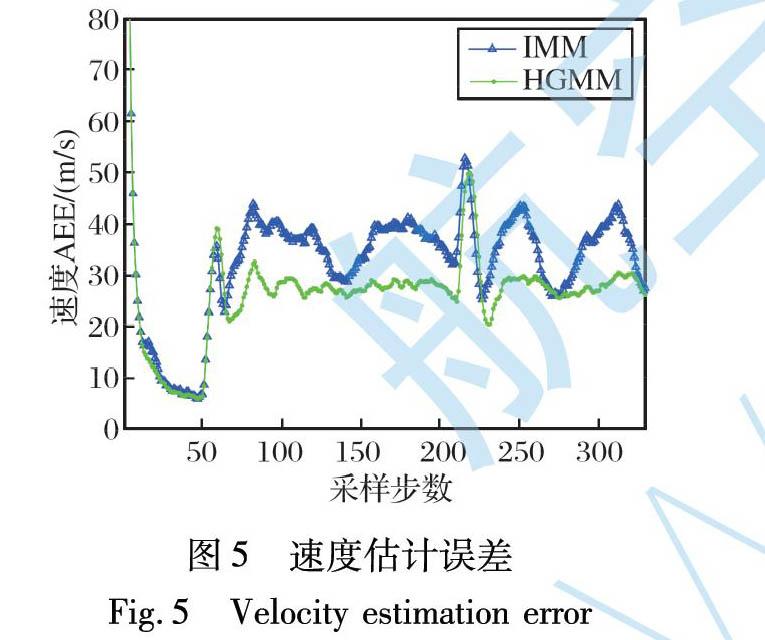
图4～5给出了两种算法500次蒙特卡洛仿真的位置和速度跟踪精度， 可以看出， 整体上HGMM具有更高的跟踪精度。

0～50步（即前5 s目标未机动时）， IMM与HGMM算法精度基本相当， 均具有较小的跟踪误差（即位置误差收敛至6 m， 速度误差收敛至7 m/s）。

50步（即5 s平飞后发生机动）后， HGMM同样具有更优越的跟踪性能（即位置收敛至12 m， 速度误差收敛至30 m/s）， 具有更低的峰值跟踪误差和更高的机动跟踪精度。 此阶段， HGMM算法输出速度估计值精度高于IMM算法输出值。

场景1目标的真实运动模式分别为-6g和8g的转弯， 意义为这些转弯运动的合加速度为6g或者8g， 当解耦到x方向或者y方向时， 其单方向的加速度大小范围为0～6g或0～8g， 而这在上述的运动模型集中确实是不存在的。 表明HGMM算法中的机动自学习算法可应对模型未知机动情况。

场景2：

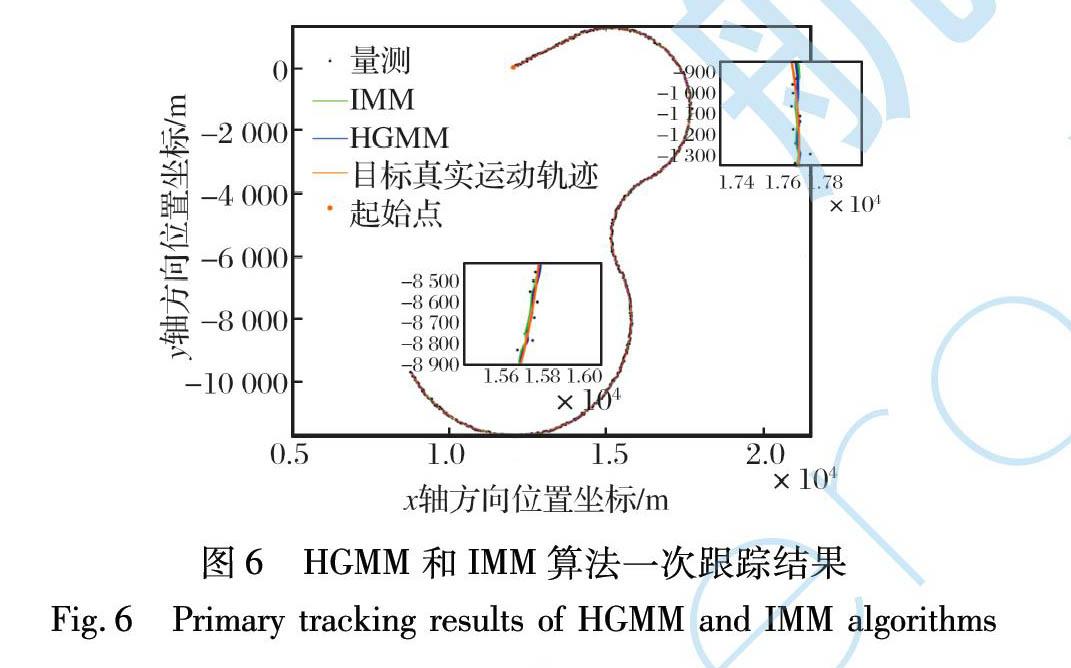
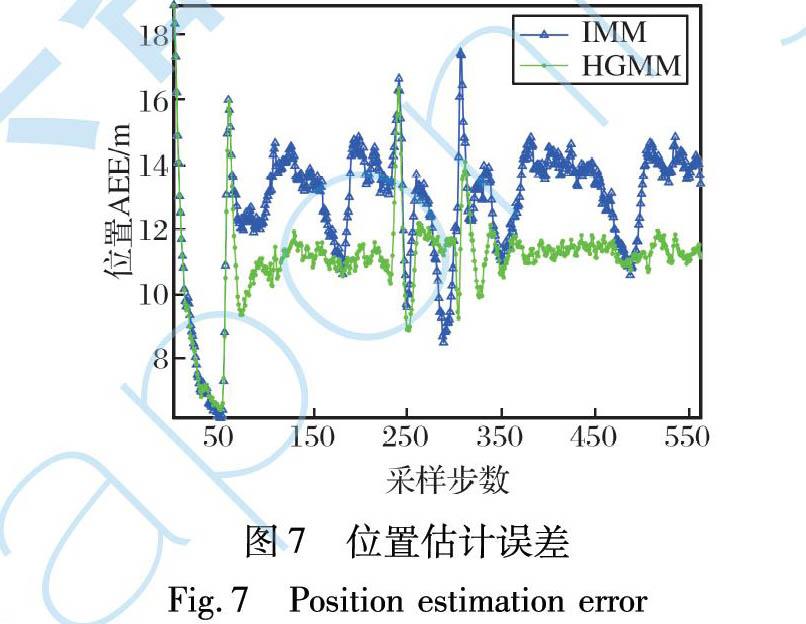
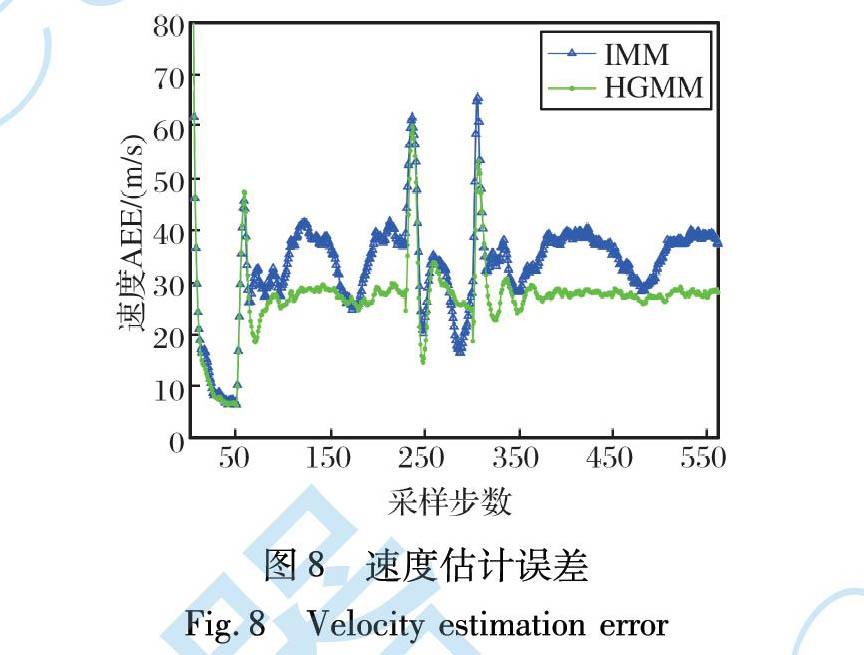
初始状态x0=[12 000 m， 400 m/s，  0 m， 200 m/s]T， 前5 s匀速运动， 之后做半个圆周的-8g转弯， 再做1/4个圆周的10g转弯， 最后做半个圆周的-5.5g转弯。 其轨迹以及两种算法的一次跟踪结果如图6所示。 两种算法的位置和速度跟踪精度如图7～8所示。

场景3：

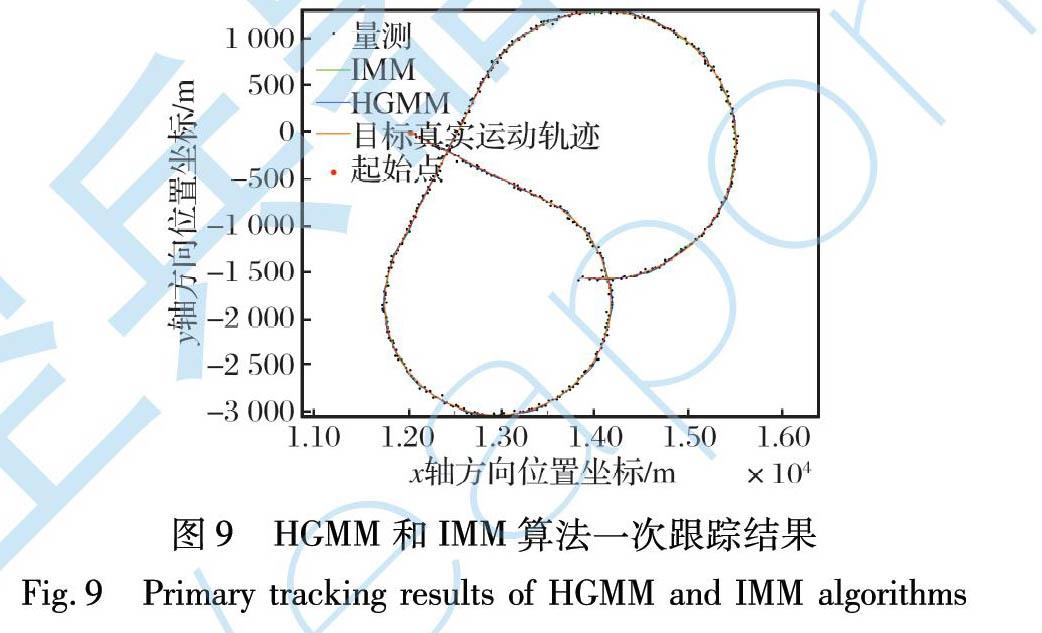
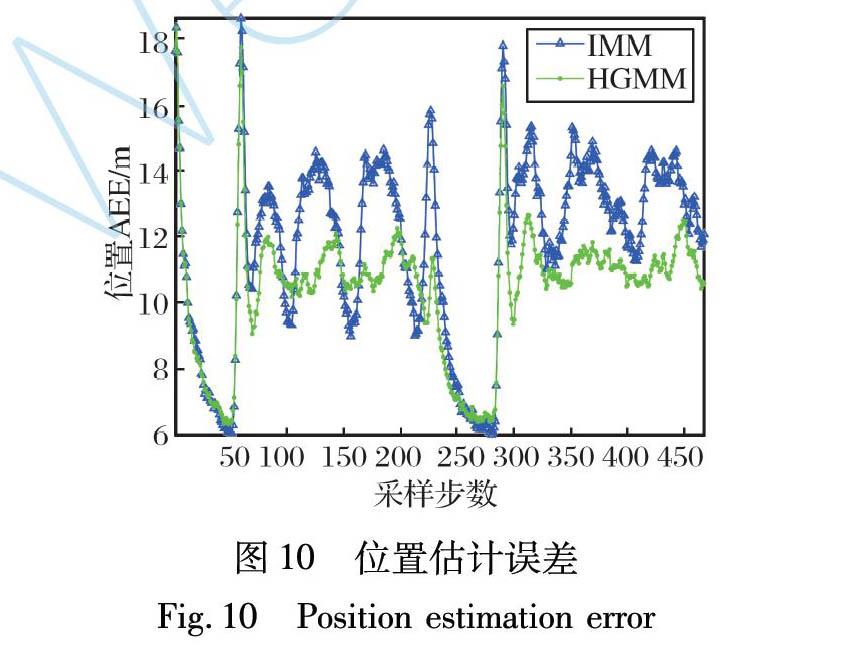
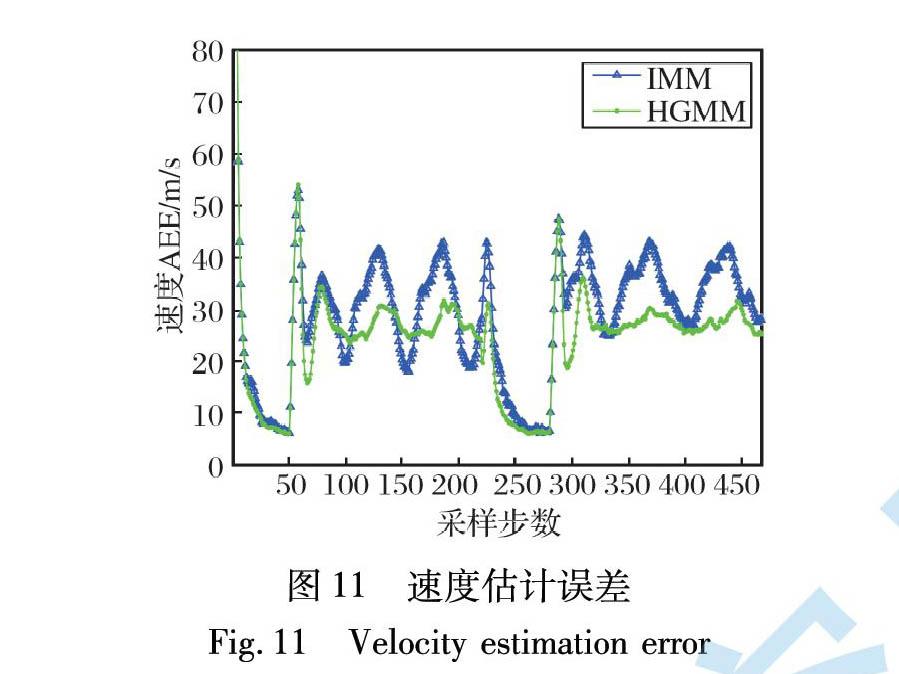
初始状态x0=[12 000 m， 300 m/s，  0 m， -150 m/s]T， 前5 s匀速运动， 之后做3/4个圆周的-9.5g转弯， 再做6 s匀速运动， 最后做3/4个圆周的-8g转弯。 其轨迹以及两种算法的一次跟踪结果如图9所示。 两种算法的位置和速度跟踪精度如图10～11所示。

对场景2与场景3仿真， 结果与场景1一致， 表明该算法适应性较好。

4 结  论

本文基于IMM框架提出的HGMM是一种稳健的具有自学习能力的高精度快速算法。 该算法能够利用少量模型集实时完备覆盖高机动目标可能的运动模式， 可有效克服高机动引起的模型失配问题， 从而提高对大机动目标运动状态的估计精度。 通过仿真可以看出， 整体上HGMM算法相对于IMM具有更高的跟踪精度， 有利于为空空导弹制导提供更准确的目标信息。

参考文献：

[1] 樊会涛， 张蓬蓬. 空空导弹临的挑战[J]. 航空兵器，  2017（2）： 3-7.

Fan Huitao， Zhang Pengpeng. The Challenges for Air-to-Air Missile[J]. Aero Weaponry，  2017（2）： 3-7.（in Chinese）

[2] 李涧青. 远程空空导弹复合制导与控制问题研究[D]. 哈尔滨： 哈尔滨工业大学，  2014.

Li Jianqing. Study on Compound Guidance and Control Problems for Long-Range Air to Air Missile[D]. Harbin： Harbin Institute of Technology，  2014. （in Chinese）

[3] 贺金萍. 空空导弹的导引与控制技术研究[D]. 南京： 南京航空航天大学，  2009.

He Jinping. Research on Guidance Law and Control Law of Air-to-Air Missile[D]. Nanjing： Nanjing University of Aeronautics and Astronautics，  2009. （in Chinese）

[4] 王国宏，  李俊杰，  张翔宇，  等. 临近空间高超声速滑跃式机动目标的跟踪模型[J]. 航空学报，  2015，  36（7）： 2400-2410.

Wang Guohong，  Li Junjie，  Zhang Xiangyu，  et al. A Tracking Model for Near Space Hypersonic Slippage Leap Maneuvering Target[J]. Acta Aeronautica et Astronautica Sinica，  2015，  36（7）： 2400-2410.（in Chinese）

[5] 吴楠，  陈磊，  薄涛，  等. 机动目标状态估计的最小均方误差界[J]. 国防科技大學学报，  2013，  35（6）： 1-8.

Wu Nan，  Chen Lei，  Bo Tao，  et al. Minimum Mean Square Error Bound for State Estimation of Maneuvering Targets[J]. Journal of National University of Defense Technology，  2013，  35（6）： 1-8.（in Chinese）

[6] Bar-Shalom Y，  Li X R，  Kirubarajan T. Estimation with Applications to Tracking and Navigation[M]. New York： John Wiley & Sons，  Inc.，  2001.

[7] Moose R L，  Vanlandingham H F，  McCabe D H. Modeling and Estimation for Tracking Maneuvering Targets[J]. IEEE Transactions on Aerospace and Electronic Systems，  1979，  AES-15（3）： 448-456.

[8] Gholson N H，  Moose R L. Maneuvering Target Tracking Using Adaptive State Estimation[J]. IEEE Transactions on Aerospace and Electronic Systems，  1977，  AES-13（3）： 310-317.

[9] Li X R，  Jilkov V P. Survey of Maneuvering Target Tracking. Part I： Dynamic Models[J]. IEEE Transactions on Aerospace and Electronic Systems，  2003，  39（4）： 1333-1364.

[10] Li X R，  Jilkov V P. Survey of Maneuvering Target Tracking. Part V： Multiple-Model Methods[J]. IEEE Transactions on Aerospace and Electronic Systems，  2005，  41（4）： 1255-1321.

[11] Xu L F，  Li X R，  Duan Z S. Hybrid Grid Multiple-Model Estimation with Application to Maneuvering Target Tracking[J]. IEEE Transactions on Aerospace and Electronic Systems，  2016，  52（1）： 122-136.

A Filtering Algorithm for Strong Maneuvering Target

Based on Adaptive Grid Mechanism

He Jingang1， 2*，  Xu Linfeng3，  Zhang Jinpeng2， Yu Zhimin4

（1.School of Astronautics， Northwestern Polytechnical University， Xi’an 710072， China;  2.China Airborne Missile

Academy， Luoyang 471009， China;

3.School of Automation， Northwestern Polytechnical University， Xi’an 710072， China;

4.The First Military

Representative Office of Air Force Equipment Department in Luoyang， Luoyang 471009， China）

Abstract：

In this paper，  a filtering algorithm for tracking strong maneuvering targets is proposed to improve the attack ability of air-to-air missiles in air combat. Firstly，  by analyzing the filtering algorithm of strong maneuvering targets，  a hybrid grid multiple model（HGMM）framework based on interacting multiple model algorithm is constructed. Then，  the hybrid grid multiple model algorithm is designed in detail. Finally，  numerical simulation shows that the proposed method is feasible and has good tracking effect，  the tracking accuracy is improved abaut 20%.

Key words：  adaptive grid; Interacting multiple model; hybrid grid multiple model;  maneuvering target; target tracking; filtering algorithm; air-to-air missile