气流柔软整理机喷射结构数值优化研究

刘 健，祝之兵，吴登昊

(1.浙江工业大学 之江学院， 浙江 绍兴 312030； 2.绍兴柯桥浙工大创新研究院发展有限公司， 浙江 绍兴 312030；3.浙江工业大学 机械工程学院， 浙江 杭州 310014)

随着国内外经济的快速发展和消费者对高档面料需求的激增，舒适环保的高档面料已成为纺织服装面料的发展趋势。织物柔软整理工艺是改善织物手感、纹理等布面风格的一种整理方法，其过程是降低纤维的刚性，降低纤维与纤维间的摩擦因数，使纤维发生松弛、滑动，最终赋予织物柔软、平滑的手感，或产生缩绒、摇粒绒等质感效果。柔软整理主要包括机械整理工艺和气流整理工艺[1]，传统的机械柔软整理工艺大多通过机械拍打或旋转的卧式滚筒等机械机构完成，该结构虽然简单，但易造成织物处理不均匀，更严重的还会造成局部坯布处理过度，造成织物损伤等。气流整理工艺由于其特有的高压气流物理处理技术得到了广泛的应用。目前国内外在气流柔软整理机的研究方面主要集中在喷射系统、自动化控制和产品整体设计等方面。在喷射系统方面，高速气流喷射技术目前是一种较先进的后处理技术，国外企业在这一领域的研发较早，其中意大利白卡拉尼公司新一代的AIRO系列气流柔软机较为成熟[2-4]。该系统可以对大部分的纺织面料进行后处理，系统集成了清洗、烘干、柔软和定形等处理工序。国内相关学者也针对气流柔软机的工作原理、气流喷射机构和相关工艺参数进行了较为系统的研究[5-7]，但是在气流喷射机构优化方面的相关研究并不多。

本文采用数值模拟方法对面料后处理结构内部气流场流动特性及气流场对面料的影响进行了研究，通过几何优化建模、网格划分、湍流模型选择、边界条件设置、流固耦合等进行计算，分析了布宽b、喷嘴数n、气腔喷嘴大小c、喷嘴倾角α、喷嘴距离面料的高度h及喷嘴间距d对面料后处理结构内部气流场的影响及气流场对面料的影响，进而获得面料处理效果最优的参数组合，为高性能面料后处理结构的优化设计提供了一定的参考。

1 喷射结构试验方案设计

1.1 正交试验方案

为了能够科学合理地安排试验，减少试验次数，缩短试验周期的同时找出面料处理结构的最优设计方案，采用正交试验法对气流喷射结构开展多方案对比研究。根据调研结果，本文设计了纺织面料气流柔软处理机内部流道结构，气流柔软机流道几何设计参数如图1所示。

图1 气流柔软机流道几何设计参数

根据研究要求，初步确定对应需要研究的6个几何因素为：布宽b、喷嘴数n、气腔喷嘴大小c、喷嘴倾角α、喷嘴距离面料的高度h、喷嘴间距d。

选用6因素3水平的L27(36)正交表，确定对应因素后，列出试验方案如表1所示。

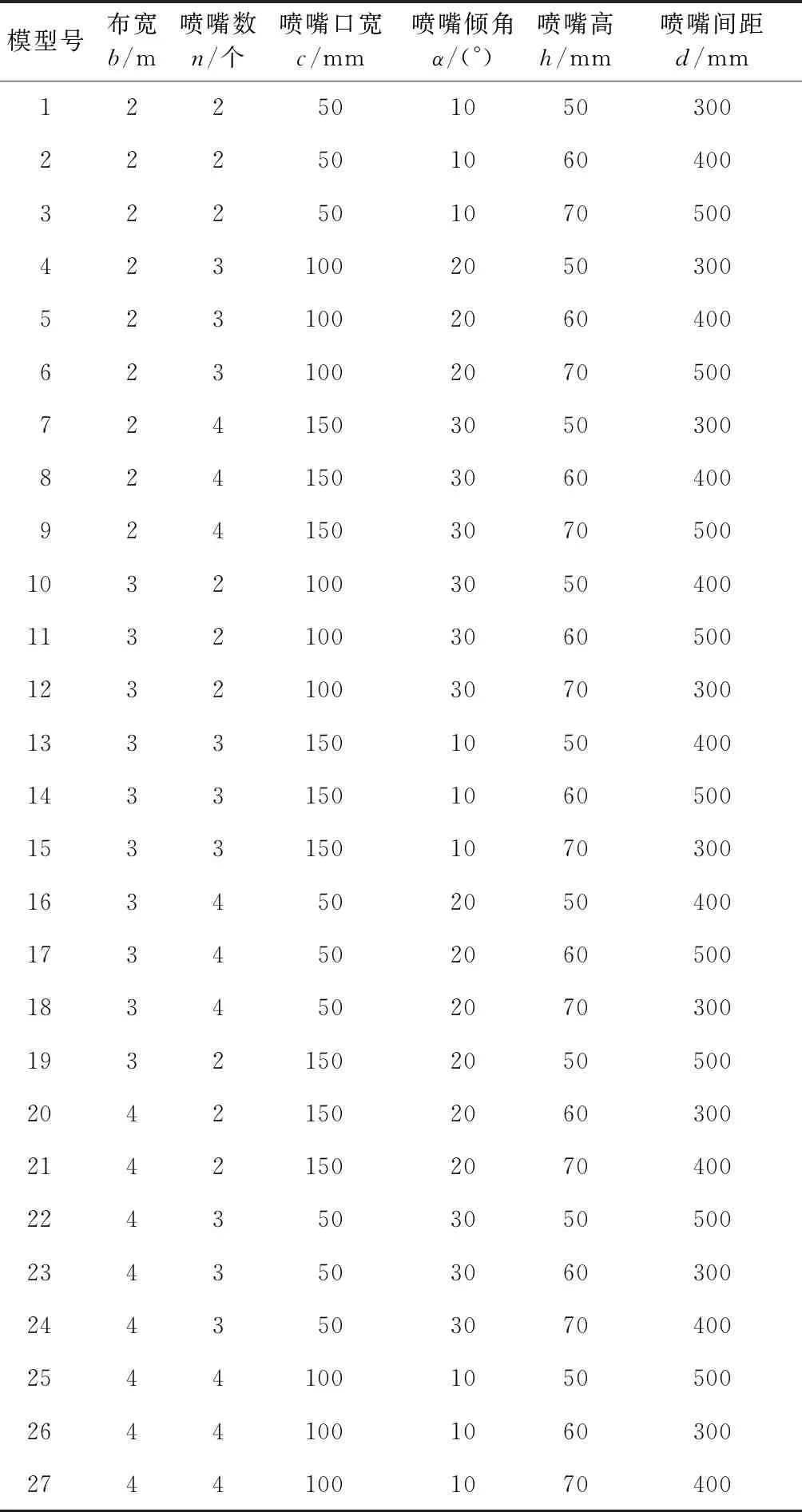
表1 不同喷嘴方案因素水平表

1.2 模型建立与网格划分

采用三维建模软件CATIA对气流柔软整理机不同喷嘴结构方案的流体域进行建模设计，气流柔软机喷射结构流体域模型如图2所示。采用网格划分软件ICEM CFD对所建模型进行网格划分。计算域采用结构化网格，结构化网格可以很容易地实现区域的边界拟合，适用于流体和表面应力集中等方面的计算。

图2 气流柔软机喷射结构流体域模型

非结构网格没有规则的拓扑结构，也没有层的概念，网格节点的分布是随意的，因此具有灵活性，应用范围较广。由于喷射结构的复杂性，同时结合结构化网格与非结构化网格对模型进行网格划分，建立优质的网格，为后续分析创造有利条件，喷射结构气流场模型网格划分及边界指定如图3所示。本文研究中气流柔软机喷射结构采用结构化网格，其他部分使用非结构化网格。

图3 喷射结构气流场模型网格划分及边界指定

2 数值计算方法

2.1 气流场数值模拟

本文采用ANSYS CFX 16.2软件对流体域进行数值计算，并采用RNGk-ε湍流模型进行求解计算。RNGk-ε湍流模型将重整的RNG理论(重整化群理论)应用到湍流流动中，属于高雷诺数湍流模型，是对标准k-ε湍流模型的一种改进。RNGk-ε湍流模型不仅充分考虑了离心泵内部流体流动中旋转和旋流情况，而且能较准确地模拟离心泵近壁区流动。RNGk-ε湍流模型[8]所用湍动能方程为:

(1)

(2)

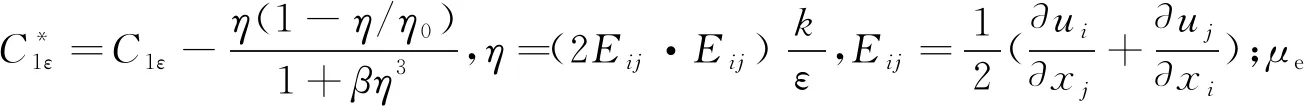
流体介质为25 ℃空气，由于压缩空气从气室中通过狭小的喷孔沿切向高速射入喷嘴揉捻腔，喷嘴中气流为黏性、可压流体。在正常揉捻过程中，喷嘴内气流可视为定常流动，不考虑纤维的存在。因此，气流柔软整理的气流场的基本控制方程表示如下：

div(ρv)=0

(3)

div(ρvv-τ)=-gradp+f

(4)

(5)

式中：ρ为气体密度，kg/m3；v为气体速度矢量，m/s；τ为黏性应力张量；p为气体压力，Pa；f为体力，一般为重力，N；T为气体温度，℃；k为气体传热系数；cp为比热容，J/(kg·K)；ST为黏性耗散项。

边界条件设置为总压力进口，参考压力为0.5 MPa；出口设置为静压出口，参考压力为0。计算流体域壁面设置为光滑无滑移壁面；各交界面模型为普通连接(General Connection)，均采用通用图像界面(GGI)网格连接方式；采用高阶求解精度，最大计算迭代步数为3 000；收敛残差RMS设置为10-5。

2.2 面料的材料参数设置

将面料的弹性参数如杨氏模量等纳入面料模型中以体现面料的弹性，面料的特性参数为：面料密度为1.2 kg/m3，杨氏模量1 430 MPa，泊松比为0.2，体积模量为7.944×108Pa，剪切模量为5.958 3×108Pa，抗拉屈服强度为63 MPa，抗压屈服强度63 MPa，最大抗拉屈服强度为86 MPa。

2.3 面料与气流耦合动力学模型

对面料气流耦合运动进行数值模拟时，首先需要建立合理的面料模型。由于面料在高速气流场中运动的过程会产生较大的位移和弯曲，而面料的应变与之相比较小，面料的运动呈现出较为明显的几何非线性特征。因此，采用完全拉格朗日表述法描述面料的运动与变形过程，即取t0=0时刻的纤维的构型作为参考构型，即变形前的构型，在所有的求解时刻待求的面料变量，都参照时刻t0=0的构型来定义。完全拉格朗日描述下经历非线性大变形的柔性纤维的动态平衡方程为：

(6)

由于面料在喷嘴气流场中运动时产生的伸长变形较小，本文假设纤维为各向同性的线弹性材料，则面料材料的本构关系式，即应力与应变的关系为：

S=DE

(7)

式中，下标0代表面料的初始构型状态；u为面料的位移矢量，m；X为变形梯度；f为体力，N；S为应力张量；D为弹性张量。

将气流柔软整理机喷嘴结构的数值模拟结果导入流固耦合(FSI)中的CFX模块；将已设置好的面料模量参数导入静力学模块中的工程数据模块；并在几何模块中建立面料模型和网格模块中进行网格划分。最后对面料气流进行两相耦合处理，首先将面料的前后端面进行固定，然后将气流压力加载到面料中。

3 结果对比分析

3.1 面料总形变量及表面相对应力分布

不同喷射模型对应的面料平均压力和平均流速如表2所示。可以发现：面料表面的平均压力及气流平均速度基本与喷嘴距离面料的高及喷嘴间距成反比关系，与喷嘴数成正比关系。由于研究模型过多，所以在本文中采用分类对比的方式进行筛选对比，进一步分析得出最佳参数组合。首先由参数布宽b，将模型分为3类，即2、3、4 m；然后在各类中喷嘴数相同的模型分为一类进行对比分析；最后进行总对比，最终得出最佳参数组合。

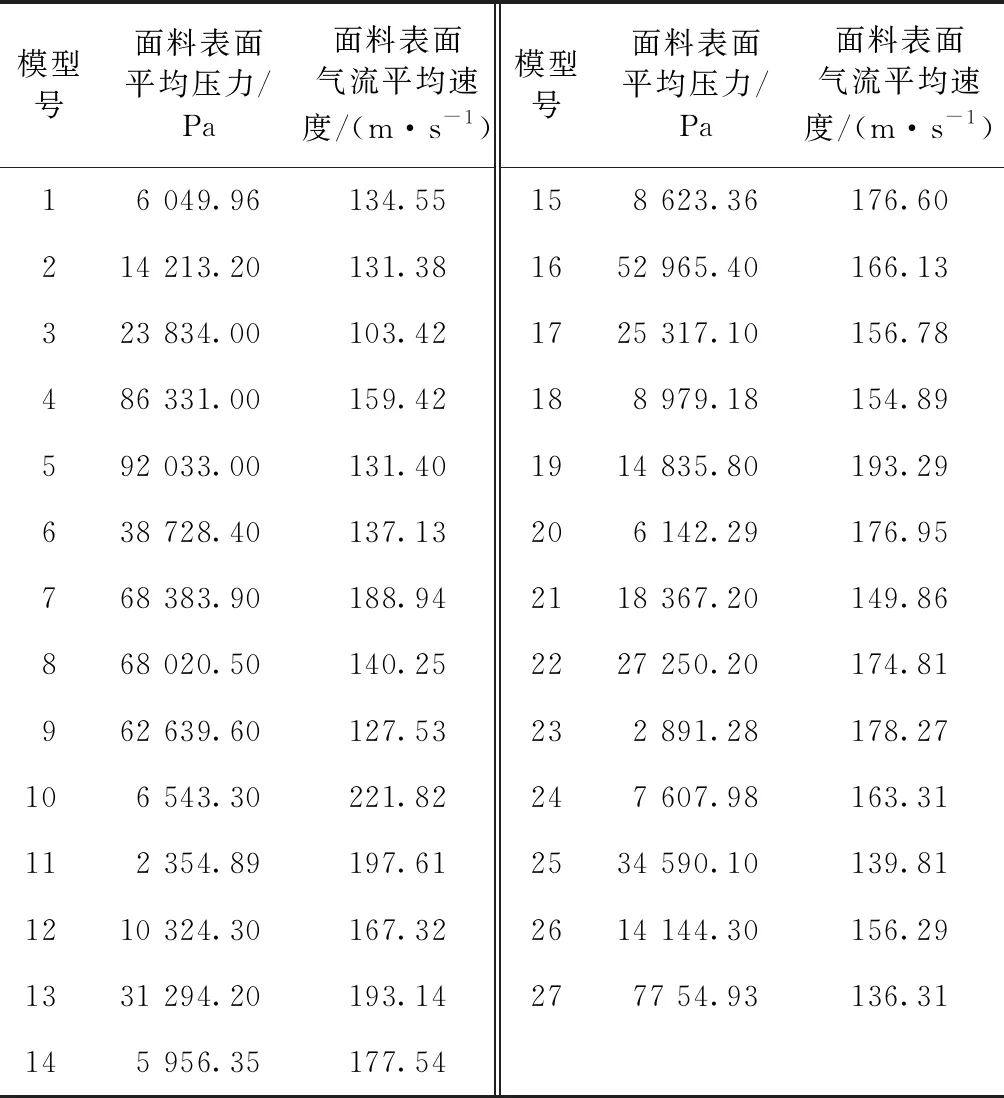
表2 不同喷射模型下面料平均压力和平均流速对比

通过类比分析得到在相同布宽、相同喷嘴数的情况下，模型1、4、7、12、13、16、19、22、25在各自类型中面料表面的平均压力及气流平均速度相对较佳。所以在接下来的研究分析中将以模型1、4、7、12、13、16、19、22、25及模型对应的面料进行对比分析。

3.2 气腔模型的静压分布及速度流线图对比分析

不同流道喷射结构压力与流线分布如图4所示，显示了部分气腔模型的静压分布及速度流线图。可以看出，气流以较高的速度通过喷嘴射入柔软处理腔，此后气流速度迅速减小。进入柔软处理腔的大部分气流沿着腔壁之间的空隙区域向前流动，从腔体出口排出。在增加喷嘴之后，面料处理腔中的高速气流回流现象只出现在第1个喷嘴后方，所以形成了一部分低压区域，但随着射流口倾斜角和射流口高度逐渐增大时，其他喷嘴后方的面料处理腔会出现气流紊乱现象，这是由于面料腔中的气流与喷嘴中的气流形成了剪切作用造成的。部分喷嘴由于其尺寸和倾角过大，导致气流在流出喷嘴之前就形成涡流现象，从而也进一步削减了气流的流速和冲击力，同时也降低了气流对面料的处理效率。通过对比发现，当增加喷嘴数后，面料处理腔中气流的静压分布及速度流线相对较平稳，没有较大的涡流出现，即可以较为均匀地作用在面料上，从而提高面料的处理效果；但增加喷嘴数后，在处理腔末端的喷嘴气流静压变低，速度变慢，也导致了面料处理效果变低。通过对比分析可得：为了能够使气流利用率尽可能达到最大，喷嘴的尺寸不宜过大；喷嘴的倾角不宜过大，大致在10°～15°之间；喷嘴数同样不宜过多；喷嘴距离面料的高度则需要根据面料本身材质的硬度进行合理的调节，但不宜过高。

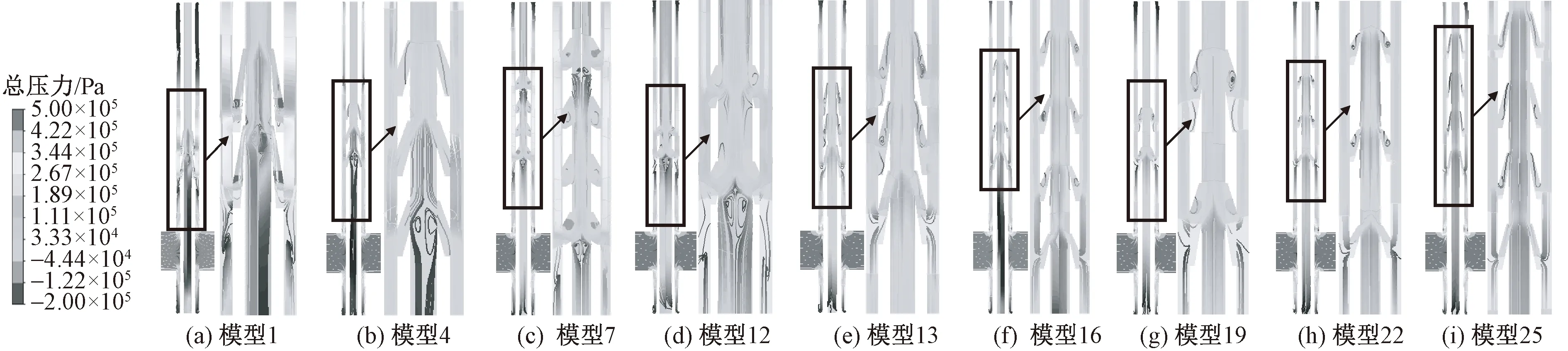
图4 不同流道喷射结构压力与流线分布

3.3 面料总形变量及表面相对应力分布

图5和图6分别为部分气腔模型中面料总形变量分布和面料表面相对应力分布。考虑实际生产中，面料处理只需要固定一端即可，面料总形变量及表面相对应力是面料处理效果重要参考参数，如果面料总形变量达不到一定的值，则对面料达不到一定的处理效果；如果面料总形变量过大或分布不均，则会使面料变形或局部变形，造成物理破坏。当然面料总形变量也可以通过调节进口气流的大小进行相应调节，本文模型对比中其面料总形变量越大，分布越均匀，即说明结构越好。对比分析部分气腔模型中面料总形变量分布可得：当布宽增大后，其最大变形量也随之增大；变形量分布均匀度与喷嘴数和布宽成正比。

图5 面料总形变量分布

图6 面料相对应力分布

对比面料表面相对应力分布，同样可以发现气腔模型25的面料表面相对应力由下到上逐渐递减，左右分布较均匀。对比分析图5、6可知，模型25对面料的处理效果最为有效。模型25的结构尺寸为布宽b为4 m、喷嘴数n为4个、气腔喷嘴大小c为100 mm、喷嘴倾角α为10°、喷嘴距离布料的高度h为50 mm及喷嘴间距d为500 mm。

4 结 论

本文根据所建立的面料在喷射结构气流场中的耦合动力学模型及其数值求解方法，对面料在其气流场中的运动规律进行了数值模拟与分析；在此基础上，进行结构改进，并运用正交试验法对几个重要的喷嘴结构参数对面料运动规律以及面料处理效果的影响进行深入研究，得出的结论如下：

通过分析面料特性和流道喷射结构特点，建立了面料与气流之间相互作用的耦合动力学模型，实现了柔性面料在流体中的流固耦合分析，为面料的流体动力特性数值模拟提供了基础。

利用正交试验法获取了不同结构参数的喷射结构模型，预测其不同参数结构对面料的处理效率的影响；分别对比分析了不同结构气流场作用下的面料形变量分布和相对应力分布，综合考虑面料表面的平均压力，平均速度，总变形量分布和应力分布的均匀性，最终确定布宽b为4 m、喷嘴数n为4个、气腔喷嘴大小c为100 mm、喷嘴倾角α为10度、喷嘴距离布料的高度h为50 mm及喷嘴间距d为500 mm的模型25为最佳方案。