苏州城北路大断面矩形顶管顶力计算与实测分析

薛青松

(中铁二十局集团第一工程有限公司， 江苏 苏州 215151)

0 引言

近十年来，矩形顶管技术的进步十分显著[1]，大断面矩形顶管在工程中的应用越来越多，但关于大断面矩形顶管的设计理念尚不成熟。当前矩形顶管建设施工主要依据《顶管施工技术及验收规范(试行)》[2]和《给水排水工程顶管技术规程》[3]，针对矩形顶管施工方法及设计的规范，如《矩形顶管工程技术规程》、《综合管廊矩形顶管工程技术标准》，正处于征求意见阶段。顶管顶力作为顶进设计的重要参数，也没有统一的国家标准计算公式。

当前，国内外的学者对于矩形顶管顶力的研究还不够完善，矩形顶管顶力的计算思路主要基于圆形顶管。顶管顶力计算中的摩阻力计算公式主要是基于Haslem提出的挖掘面稳定假设[4]和O'Reilly等提出的管土全接触假设[5]。基于以上理论推导出的公式形式上基本可以分为3类： 理论公式、半经验公式和经验公式[6]。其中，林越翔等[7]通过分析已有矩形顶管管壁摩阻力计算公式，运用普氏压力拱理论和土柱理论，通过对圆角部分进行积分，推导了深埋和浅埋仿矩形顶管管壁摩阻力的计算公式； 熊翦[8]基于卸荷拱理论探讨了在埋深较大条件下矩形顶管的顶力计算方法； 冯超[9]运用修正的太沙基理论，推导了矩形顶管理论顶力计算公式。

本文在研究现有计算模型及存在问题的基础上，结合矩形顶管的特殊性探究大断面矩形顶管顶力计算模型。在比尔鲍曼理论、管土与管浆部分接触理论基础上修正改进，充分考虑泥浆对管节浮力的影响，推导出大断面矩形顶管的顶力计算方法，并依托苏州城北路大断面矩形顶管工程案例，对比分析计算值与实测值，验证计算模型的科学性与合理性。

1 现有计算模型研究及存在问题

1.1 垂直土压力模型

垂直土压力模型是顶管顶进计算中的关键因素。矩形顶管相较于圆形顶管更易产生滑裂面，不易形成压力拱，因此，目前采用的太沙基、马斯顿等垂直土压力计算模型不适用于大断面矩形顶管垂直土压力计算。

1.2 未考虑管节在泥浆中的状态

膨润土泥浆在管土之间形成的泥浆套对管道有一定的托浮力，管道在泥浆中有3种存在状态，即下沉、悬浮和上浮。假设注入的泥浆均匀且没有压缩性，取苏州3个顶管施工案例进行计算，各案例管节所受泥浆浮力如表1所示。由此可以确定，大断面矩形顶管在顶进过程中, 泥浆浮力大于管节的重力，且随着管节断面面积的增大，泥浆浮力与管节的重力差距增大。

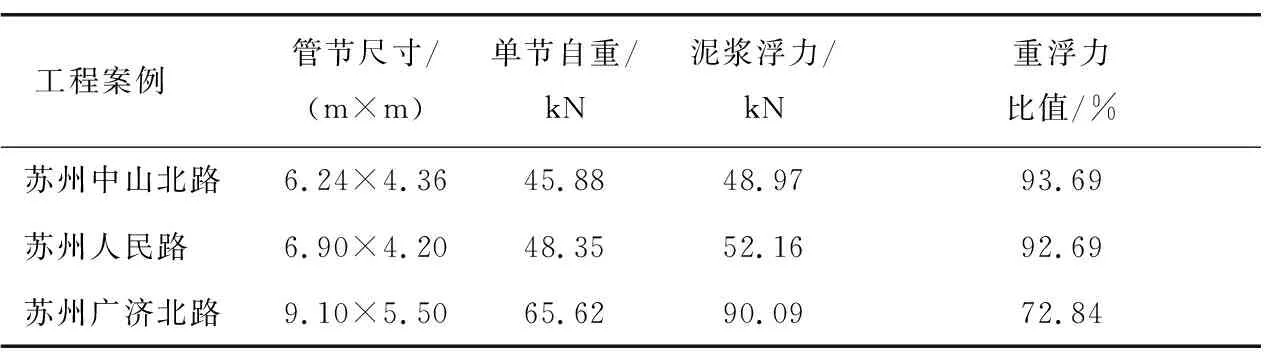
表1 部分顶管案例管节所受泥浆浮力

1.3 未考虑顶管机机头摩阻力

目前在一些规范和顶力计算公式中，通常忽略了顶管机机壳的摩阻力，或将顶管机机壳等同于管节进行计算。实际上，顶管机机壳为钢材料，顶管机机壳的自重分布与管节有较大差别； 顶管机机壳尺寸略大于管节尺寸，与土体接触更加紧密，摩擦因数的选择并不一样； 断面面积越大，误差会越大。因此应将顶管机机壳单独进行受力分析。

2 大断面矩形顶管顶力计算模型

2.1 顶力的构成和受力分析

结合各种规范公式及矩形顶管的特殊性，大断面矩形顶管的顶力

F=Fp+F1+F2。

(1)

式中：F为总顶力，kN；Fp为迎面阻力，kN；F1为顶管机机壳的摩阻力，kN；F2为管节的摩阻力，kN。

基于O'Reilly等的管土全接触假设，顶管在竖直方向上受到垂直地层压力、管体自重、地基支反力； 在水平侧方向上受到水平地层压力，如图1所示；在轴向上受到顶管机机头部分的迎面阻力Fp、分布在管节周围的摩阻力F2以及顶管机机壳周围的摩阻力F1，如图2所示。

图1 矩形顶管横截面受力示意图

图2 矩形顶管顶力构成

2.2 垂直土压力计算

垂直土压力计算方法主要采用土柱理论、普氏卸荷拱理论、太沙基理论、比尔鲍曼理论。

土柱理论，如图3所示，认为隧道顶部垂直土压力大小等于上覆土体的自重。该方法适合于埋深较浅、土体变形较小的软土地层。

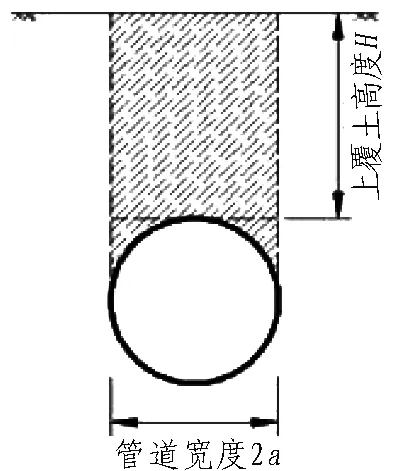
图3 土柱理论示意图

普氏卸荷拱理论认为在松散介质中开挖隧道后，在隧道上方会形成抛物线形的平衡拱，而作用在隧道顶部的竖向土压力仅取决于拱以下土体的重力，与埋深无关。该理论适用于埋深足够大且土体具备一定抗剪强度的工况。普氏压力拱如图4所示。

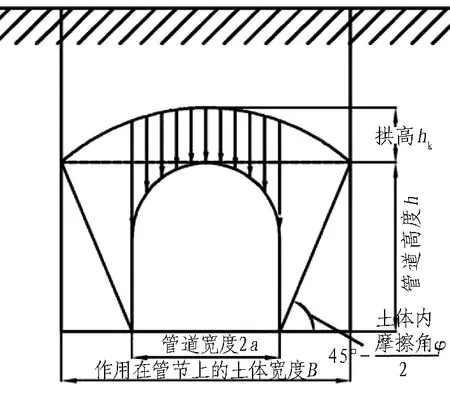
图4 普氏压力拱示意图

太沙基理论[10]，如图5所示，以松散介质极限平衡理论为基础，认为在开挖隧道后，隧洞顶部覆土的变形大于两侧土体的变形，管顶土体自重将通过剪力传递扩散给两侧土体。该理论适用于埋深较大的隧道。

图5 太沙基理论示意图

大断面矩形顶管工程一般属于浅埋隧道，结合竖向土压力理论适用条件，普氏卸荷拱理论和太沙基理论适用于埋深较大、土质较好的工况，并不适用埋深较浅的工况。比尔鲍曼理论，如图6所示，也称修正的土柱理论，认为地下洞室上覆土层向下滑动时土柱两侧产生2个滑动面，其起点在墙基，与垂线的夹角为45°-φ/2，则作用在地下洞室上方的土层压力为土柱的自重减去两侧面的夹制力，其计算公式为：

pU=2aσv。

(2)

σv=kγH。

(3)

(4)

k1=tan2(45°-φ/2)tanφ。

(5)

k2=tan(45°-φ/2)tanφ。

(6)

a1=a+htan(45°-φ/2) 。

(7)

式(2)-(7)中：pU为单位长管道上部压力； 2a为管道宽度，m；σv为顶部竖向土压力，kPa；γ为土体容重，kN/m3；H为上覆土高度，m；k、k1、k2为计算系数； 2a1为作用在管道上的土柱宽度，m；c为土的黏聚力，kN/m2；φ为土的内摩擦角，(°)；h为管道高度，m。

图6 比尔鲍曼理论示意图

2.3 侧向土压力计算

在顶进过程中，大断面矩形顶管的断面开挖尺寸比管节尺寸要大20～30 mm。断面开挖后，土体会逐渐向管节方向变形至贴合，并产生主动土压力。各规范中侧压力计算均采用的是主动土压力系数，故侧压力

pR=Ka(σv+h/2)H。

(8)

式中：pR为单位长度管道侧压力，kN/m；Ka为主动土压力系数，Ka=tan2(45°-φ/2) 。

2.4 地基反力计算

地基反力属于被动抗力，其分布形式与上部荷载和下部土层条件相关。矩形顶管施工荷载较为复杂特殊，因此，地基反力不能简单认作与作用荷载相平衡的反作用力。施工过程中的正面附加应力、侧面摩阻力、地层损失、注浆填充等因素对土体变形都很关键[11]，所以不能简单将地基反力表示为顶部土压力与其自重之和。目前对管底支反力的处理方法有试验分析法、Winkler地基解析法、经验假定法以及弹性理论分析法等[12]。对于圆形顶管，中国和德国的顶管规程均采用克莱茵分布模式； 就矩形顶管应用而言，Winkler地基解析法较为适宜。Winkler地基解析法假定地基由一系列独立的弹簧组成，地基反力和变形成线性比例增加。利用基于该模型的地基反力曲线，在矩形顶管开挖变形小的前提下，对管土地基反力进行推导分析[13]。图7示出地基反力曲线，反应了土压力系数随土体位移的变化趋势。

图7 地基反力曲线图

矩形顶管地基反力计算公式为：

(9)

pD=KwUw(pU+G-F浮) 。

(10)

式(9)-(10)中：Kw为土压力系数；K0为静止土压力系数，K0=1-sinφ；Kp为被动土压力系数；n为地基反力系数，n=Kw/pU；pD为单位长度地基反力,kN/m；Uw为土体竖向变形，m；G为单位长度顶管重力或单位长度顶管机重力，kN/m；F浮为单位长度泥浆浮力，kN/m。

2.5 迎面阻力计算

何莲等[14]通过对土压平衡和泥水平衡顶管的分析，认为在正常施工中，迎面土压力控制在主动和被动土压力之间，为静止土压力的1.0～1.1倍。因为迎面顶力一般需要与迎面土体压力保持平衡，若迎面顶力大于被动土压力，则会挤压土体，使地表产生隆起； 若迎面顶力小于主动土压力，则开挖面不能保持稳定，容易坍塌，使上部地表产生沉降。结合目前顶管施工对周围地层的影响规律，当顶管顶到某一地段时，一般地表会产生隆起[15]，说明顶力是大于静止土压力的。结合文献[14]的理论，本文更倾向于迎面阻力取1.1倍静止土压力。

掌子面上土压力呈梯形分布，土压力作用点位于重心上,则迎面阻力计算公式为：

(11)

式中s为管节断面面积，m2。

2.6 摩阻力计算

目前，国内顶管摩阻力计算主要是管周土压力乘以摩擦因数。由于摩擦因数取值依靠经验，计算结果忽高忽低，且没有考虑泥浆套对于管道的影响。在注入减阻泥浆情况下，摩阻力由管土摩阻力和管浆摩阻力共同构成，即同时存在固-固和固-液接触状态[16]。

根据1.2节对大断面矩形顶管在泥浆套中的状态分析，其处于上浮的状态，即管顶与土体接触，管壁两侧与底部充满泥浆。由于顶管顶进速度较慢，可将顶进过程视为匀速状态。顶进过程中，土体不发生位移，可将土体-泥浆-管壁相互作用模式简化为平板流行模型。

泥浆流变性能一般用流变性能曲线描述。顶管工程用泥浆通常为膨润土体系泥浆，可将其流型视为宾汉塑性模型，如图8所示，其表达式为：

(12)

式中：τf为剪切应力，kPa；ηp为塑性黏度，Pa·s；v为顶管平均顶进速度，m/s；i为泥浆套厚度，m；τ0为动切应力，Pa。

图8 宾汉塑性模型

ηp可采用六速旋转黏度计测出，也可根据泥浆配方取经验值；i取施工空隙大小，即泥浆套厚度。

泥浆两侧及下部摩阻力为：

Fw=τf(m-2a)l。

(13)

式中：Fw为管浆摩阻力，kN；m为顶管机周长，m；l为顶进距离，m。

矩形顶管顶部与土体接触，摩擦力

Fg=pUf1l。

(14)

式中：Fg为管土摩擦力，kN;f1为管节与土体摩擦因数。

管节摩阻力

F2=Fw+Fg=τf(m-2a)l+pUf1l。

(15)

由于顶管机机壳与周围土体紧密接触，施工空隙较小，所以顶管机机壳四周均应该按照摩擦力计算公式计算，其摩阻力为：

F1=(pU+pD+2pR)f2l壳。

(16)

式中：f2为顶管机机壳与土体的摩擦因数；l壳为顶管机机壳长度，m。

2.7 大断面矩形顶管顶力计算公式

根据以上推导，大断面矩形顶管顶推力为：

(17)

式(17)的适用条件为： 1)顶管属于浅埋，即上覆土厚度小于顶管的1.5倍跨度； 2)矩形顶管断面在5 m×5 m及以上； 3)不考虑顶管纠偏引起的摩阻力上升； 4)注浆效果良好，采用触变泥浆减阻，注浆量要足够； 5)钻进地层无特殊地层，如漏失、强研磨性岩层等。

3 工程实例

3.1 工程概况

苏州市城北路综合管廊某标段顶管工程位于苏州市城北东路与齐门北大街相交处附近，顶进长度为233.6 m，顶管施工段平均覆土厚度为9 m。综合管廊断面尺寸为5.5 m×9.1 m，壁厚为650 mm，管节断面结构如图9所示。管节长度为1.5 m/节，单节质量约66.8 t。采用土压平衡方式进行施工，在泥土舱布置有土压力计，在顶进施工期间对顶进油缸和土压力计的数据及顶进距离进行记录。

图9 管节断面结构 (单位： mm)

该工程顶管施工穿越地层主要为粉砂夹粉土、粉砂层，潜水最高水位为2.63 m，最低水位为-0.21 m，地下水年变幅为1～2 m。顶管地层参数如表2所示。

表2 顶管地层参数

苏州城北路矩形顶管工程主要计算参数如表3所示。

表3 城北路顶管工程主要计算参数

Table 3 Main calculation parameters of Chengbei Road pipe jacking project

计算参数取值顶进距离/m233.60机壳尺寸/(m×m)9.12×5.52管节尺寸/(m×m)9.10×5.50管节圆角/m0.65管节自重/(kN/m)432.00机壳自重/kN2 000.00机壳长度/m5.00摩阻系数下限0.07计算参数取值上覆土高度/m9土体平均重度/(kN/m3)20土体内摩擦角/(°)28平均土体黏聚力32泥浆黏度/s48塑性黏度/(mPa·s)25泥浆动切应力/Pa15摩阻系数上限0.1

3.2 总顶力计算分析

将本文推导的顶推力计算公式及《给水排水管道施工及验收规范》(规范1)、《顶管施工技术及验收规范(试行)》(规范2)、《日本下水道协会计算公式》(规范3)公式应用于苏州城北路矩形顶管的顶力计算中，计算结果和实测值如表4所示。

表4 顶力计算结果和实测值

由表4可知，实测顶力值明显小于总顶力上限值，因此取各计算公式的总顶力下限值做柱状图进行分析，如图10所示。

资管新规对理财产品的冲击主要来源于取消刚性兑付的规定。一方面,“金融机构开展资产管理业务时不得承诺保本保收益”这一新规定，说明保本理财将彻底退出市场，目前这一块的规模在7.37万亿元。另一方面，通过 “金融机构对资产管理产品应当实行净值化管理”这一新规定，能够采取摊余成本的封闭式产品仅有一小部分，这样一来，非保本理财的稳定高收益光环就会消失，投资吸引力也逐渐降低，最终产生非保本理财规模萎缩的情况。另外，作为银行理财重要投资途径的通道业务也在资管新规中被重新定义，也对银行发行理财产品的积极性起到了一定的阻碍作用。

由图10可知，各公式顶力计算均大于实测顶力，说明顶管工程注浆减阻效果良好。

规范2基于管土全接触假设的理论公式，采用周围土压力乘以管土摩阻系数，并未考虑泥浆套的形成及顶管在泥浆套中的状态。规范1、规范3均是经验公式，相较之下均能较好地贴合实际工程的顶力计算，其经验系数的选取考虑了各种因素的影响，参考了大量工程实例，具有较高的实用价值，但对于不同地区的适用性较窄，不同地区不同工程经验系数的差别较大。

本文推导的理论计算公式计算值与实测值的相对误差较小，主要特点如下：

图10 总顶力对比分析

1)采用比尔鲍曼理论计算顶部压力，考虑了两侧土体对于土柱的钳制作用，将土体的摩擦角及黏聚力纳入计算范围，相较于传统的土柱理论，更加全面。经计算，采用比尔鲍曼理论计算的土压力为土柱理论的81.6%。

2)对顶管机机壳的摩阻力进行单独计算，由于顶管机机壳与周围土体的施工间隙很小，无法形成稳定的泥浆套，其摩擦因数与管节摩擦因数差别较大。经计算，顶管机机壳摩阻力达3 154.55 kN,是迎面阻力的30%左右。

3)充分考虑了泥浆套的形成及顶管在泥浆套中的状态，同时考虑了管土摩阻力和管浆摩阻力。对于管浆接触部分，采用流体力学的平板理论进行分析。经计算，单位长度摩阻力为101.86 kN/m，是《顶管施工技术及验收规范(试行)》的30%左右。

3.3 实测顶力曲线

顶力对比分析如图11所示。由图可知： 初始顶力大，顶力上升趋势较缓，顶力曲线呈台阶式波动上升，这主要是由顶管正常顶进或施工停顿后重新顶进时泥浆的触变性导致的。顶进前10 m，顶力较计算值大很多，主要是因为该阶段未注入减阻泥浆。

规范2计算公式较为保守，在60 m左右就已超过实测顶力，顶进结束时已经达到实测顶力的2倍左右。规范1、规范3在顶进距离超过70 m后与实测顶力有较好的契合，其中本文公式与实测曲线的拟合程度最好，初始顶力最接近实测顶力，说明单独计算顶管机机壳摩阻力较为合理。

图11 顶力对比分析

3.4 单位长度摩阻力分析

通过将总顶进力减去泥土舱压力并除以顶进距离得到实测的单位长度摩阻力。

单位长度摩阻力对比分析如图12所示。由图可知，在顶进前10 m时，实测顶力单位长度的摩阻力很大且急剧下降。这是因为该阶段没有使用润滑泥浆导致摩阻系数较大，随着减阻泥浆的注入，单位长度顶力开始逐渐减小并稳定下来。

规范2计算公式单位长度摩阻力在50 m以前与实测单位长度顶力有一定的吻合性，但超过50 m后，单位长度顶力稳定后，计算值与实测值差别较大，几乎达到实测值的3倍。本文计算公式及规范1计算公式的单位长度摩阻力与实测值的吻合性最好，当泥浆套稳定后，实测单位长度顶力在该计算值上下波动。

图12 单位长度摩阻力对比分析

4 结论与建议

本文基于比尔鲍曼理论和管浆部分接触泥浆套理论，推导了大断面矩形顶管顶力的计算公式。同时，结合工程案例进行顶力计算的对比，对推导公式进行验证并分析其他计算公式的适用条件，主要得出以下结论：

1)通过对大断面矩形顶管截面积与埋深进行分析，采用比尔鲍曼理论计算上部土压力更为合理。

2)通过分析大断面矩形顶管在泥浆套中的状态，提出摩阻力由管土摩阻力与管浆摩阻力共同构成。

3)本文推导的矩形顶管顶力计算公式考虑了机壳摩阻力，迎面阻力取1.1倍静止土压力，同实际情况吻合度高。

4)根据《给水排水管道工程施工及验收规程》得出的矩形顶管顶力表达式清晰简洁，计算结果同工程实测值较为接近，工程适用性较好。

5)顶管施工中，实际顶力是动态波动变化的，受很多因素影响。在总顶力计算及配置中，应该考虑一些现场不利因素，考虑一定的安全储备。