EM聚类方法在岩性复杂区水系沉积物地球化学异常圈定中的应用

孙尧尧，郝立波，赵新运，陆继龙，马成有，魏俏巧

(吉林大学 地球探测科学与技术学院，吉林 长春 130026)

0 引言

在地球化学找矿工作中，异常的圈定是极为重要的环节。目前，在岩性复杂区水系沉积物地球化学异常圈定时仍存在一些亟待解决的问题，其中，岩性背景问题最为突出，尤其是在区域地球化学勘查中[1-4]。若不消除岩性背景差异的影响而直接采用统一的背景上限进行异常圈定，一是可能会将高背景值区的一些正常样品划分为异常样品，从而形成虚假地球化学异常；二是可能会将低背景值区的一些异常样品划分为正常样品，从而掩盖掉部分低弱但重要的地球化学异常[3-5]。

针对岩性背景问题，学者们提出了许多处理方法，如多元线性回归法[6]、滑动平均标准化法[1]和一元线性回归法[3-4]等。然而，这些方法的提出并不是从直接区分岩性背景的角度出发的，或多或少存在一些局限性，因此很难从根本上消除岩性背景的影响。Zhao等认为岩性背景问题的本质是多重母体问题，因此提出利用Expectation-Maximization(EM)算法来分解多重母体，进而达到消除岩性背景影响的目的[5]。该方法地质意义明确，对合理圈定岩性复杂区水系沉积物地球化学异常应能起到一定的作用。笔者以湖南省某地1∶20万水系沉积物地球化学数据为例，尝试将EM聚类方法应用到地球化学背景与异常划分中，旨在为岩性复杂区水系沉积物地球化学异常的圈定提供参考。

1 岩性背景问题

研究表明，地球化学背景与异常划分的影响因素主要有岩性背景、地球化学景观条件以及样品粒度等[1-2,6]。但在相同或相近的景观条件下，岩性背景的影响最为突出[3-4]。岩性复杂区往往存在多种岩石类型，不同类型岩石的元素丰度通常存在明显差异。研究表明，岩性单一的地质体的元素含量往往服从(近似)正态分布[7-8]，其数据可构成一(近似)正态分布的母体。因此，岩性复杂区应存在多个(近似)正态母体。岩石风化形成的水系沉积物对基岩的化学成分具有显著的继承性[9-10]，因此岩性复杂区水系沉积物元素含量数据内也应包含多个(近似)正态母体[5]。来源于不同岩性背景的元素含量数据发生混合，即正态母体混合或正态分布叠加，可产生偏态分布，包括左偏、右偏及多峰等分布型式[7-8]，这是岩性背景对地球化学异常圈定的直接影响。由此可见，岩性背景问题即多重母体问题，而多重母体问题主要源于岩性背景差异。

针对上述问题，学者们开展了大量的研究工作，提出了许多处理方法。研究表明，在使用任何数据处理方法划分地球化学背景与异常之前，应先确定元素含量的概率分布型式，且以(近似)正态分布为目标[11]。为满足正态分布的前提，一些数据变换方法被应用到异常圈定中，如对数变换法[12-13]、倒数变换法[14]和Box-Cox变换法[15]等，其中对数变换法最为常用。Stanley研究指出，对数变换及类似的数学变换方法通常难以消除地球化学数据偏态分布的特征[16]。在地球化学数据处理工作中，这一现象是普遍存在的，通常是偏态分布经对数转换后仍不服从(近似)正态分布。然而，这些方法目前仍被广泛使用，可能已经造成了严重的错误。

按地质单元界线区分岩性背景的效果也不是很理想，原因是同一地质单元的岩性组成往往并不单一，即同一地质单元内也可能含有多个(近似)正态母体。因此，一些学者尝试从回归分析的角度来解决岩性背景问题。周蒂提出了多元线性回归分析方法[6]，郝立波等提出了一元线性回归分析方法[3]。相比于传统的数据变换处理方法，这些方法具有很大的优势，可以在一定程度上消除岩性背景的影响，较准确地划分出成矿元素的地球化学背景与异常。然而，回归分析方法也有其局限性，因为该类方法仅适用于那些与岩性存在良好线性关系的成矿元素，而不适用于那些受岩性背景影响小或不受影响的元素。另外，线性回归分析要求残差符合正态分布，这也是该方法使用受限的原因之一。

李宝强和孙泽坤提出了滑动平均标准化方法[1]，其不足之处是窗口大小的确定具有很大的人为性，若窗口过大，则难以消除元素背景含量的影响，而窗口过小，又会缩小各点的元素含量差异，损失异常信息。至于分形/多重分形方法，对于服从分形分布的元素含量数据，该类方法可能是一种很好的选择[17-18]，然而，该类方法的地质和地球化学意义仍不明确[3-5,19]，另外，该类方法也无法区分来自不同岩性母体的样品。同样地，线性判别分析方法[8,20]和概率格纸法[21]等也面临同样的问题，即无法判别样品具体归属于哪一类岩性母体[5]。

解决岩性背景问题的根本途径应是直接区分岩性背景或分解多重母体。Zhao等研究认为，在岩性复杂区可利用能反映岩性变化的主量和(或)亲石微量元素，通过EM聚类算法——一种有效的高斯混合模型聚类方法，对来自不同岩性背景的水系沉积物样品进行分类，以达到区分岩性背景或分解多重母体的目的[5]。基于此，笔者以湖南省某地1∶20万水系沉积物地球化学数据为例，尝试采用EM聚类方法进行多重母体分解，然后进行地球化学异常圈定，并将其与传统的均值+k倍标准偏差方法圈定的异常进行比较。

2 方法流程

2.1 样品分类

样品分类主要基于EM算法。该算法由Dempster等提出[22]，是一种重要的统计学分析工具，已被广泛应用于含有隐变量的概率模型参数的极大似然估计中。假设在某一复杂岩性区采集了n个水系沉积物样品，其分析结果可设为随机变量X，X=(x1,x2,x3,…,xn)，样品采自不同的岩性背景区，即X内含有多个正态母体，但每个样品的对应母体或类别是未知的。正态母体的分布参数也是未知的，样品的对应类别可设为变量Z，Z=(z1,z2,z3,…,zn)。EM算法是先初始化正态母体的分布参数θ，然后重复以下两个步骤：①根据分布参数θ计算样品分类变量Z的期望，Qi(zi)=p(zi|xi;θ)；②将概率模型参数的似然函数L(θ)最大化以获得新的分布参数θ，即

似然函数L(θ)收敛时，迭代停止。最终，可得到样品的具体分类情况，即在寻找最优参数来极大化样本似然函数的过程中对样本完成最优分类[5]。

在实际问题处理中，应首先根据研究区地质概况选取可以反映岩性变化，且元素间相关性较小的非成矿常量和(或)亲石微量元素作为聚类指标，然后采用EM算法对样品进行分类。最优分类数可采用数学衡量指标和地质条件双重限制进行合理判别[5]。数学衡量指标为赤池信息量准则AIC(akaike’sinformationcriterion)，一个衡量模型拟合程度的标准[23]。AIC可以表示为：

AIC=2k-2ln(L)。

式中：k是模型的独立参数个数；L是模型的极大似然函数。按极大似然函数准则，L越大，模型的拟合度越高，但实际上，在L过大的情况下，可能会出现过拟合现象。为了避免过度拟合，AIC准则在追求L尽可能大的同时，还要求模型参数要尽可能少，即k要尽可能小，换句话说，AIC值越小，模型的拟合情况越好。因此，在有限混合正态分布参数的极大似然估计中，当AIC值达到最小时可获得最优分类数。采用地质条件限制时，可先根据分类结果绘制分类图，然后将其与地质图进行对比，与地质图吻合度最高的分类图对应的分类数可确定为最优分类数。按统计学的要求，每个分类中样品数应不少于30个，若不满足，则需调整分类，或将样品数较少的类合并到与其最近的类中。

2.2 数据标准化

样品分类完成后，对每个分类中的样品成矿元素含量数据进行3S检验，将均值±3倍标准偏差范围外的异常数据剔除。然后，利用剩余数据计算每个分类中成矿元素含量的均值和标准偏差，以此对成矿元素的含量进行Z分数标准化，公式如下：

i=1,2,3,…,n;j=1,2,3,…,m。

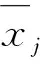
2.3 异常圈定

经样品分类和元素含量标准化后，岩性背景差异在一定程度上得到了消除。因此，可在全区采用统一的背景上限进行异常圈定，即直接采用传统的均值加k倍标准偏差的方法或其他方法进行异常圈定，k值的大小可依据实际情况进行适当调整。

3 应用实例

3.1 研究区概况

以湖南省某地1∶20万水系沉积物地球化学数据为例，进行了基于多重母体分解的地球化学异常圈定试验。研究区面积约为4 300 km2，水系沉积物样品数为1 050，采样密度约为1个样品/4 km2。水系沉积物化学成分分析项目包括Ag、As、Au、B、Ba、Be、Bi、Cd、Co、Cr、Cu、F、Hg、La、Li、Mn、Mo、Nb、Ni、P、Pb、Sb、Sn、Sr、Th、Ti、U、V、W、Y、Zn、Zr、Al2O3、CaO、Fe2O3、K2O、MgO、Na2O及SiO2。研究区发育有多个钨锡多金属矿床，成矿地质条件优越。研究区地层复杂，但岩性较为简单，按照出露面积从大到小的排列依次为上古生界灰岩、泥灰岩，下古生界浅变质砂岩，白垩系砂岩，泥盆系砂岩和震旦系砂质板岩。研究区侵入岩主要为印支期和燕山期二长花岗岩，分布于研究区中部偏西处。区内发育有多条走向近SN和NW的断裂(图1)。

图1 研究区地质简图Fig.1 Schematic geological map of the study area

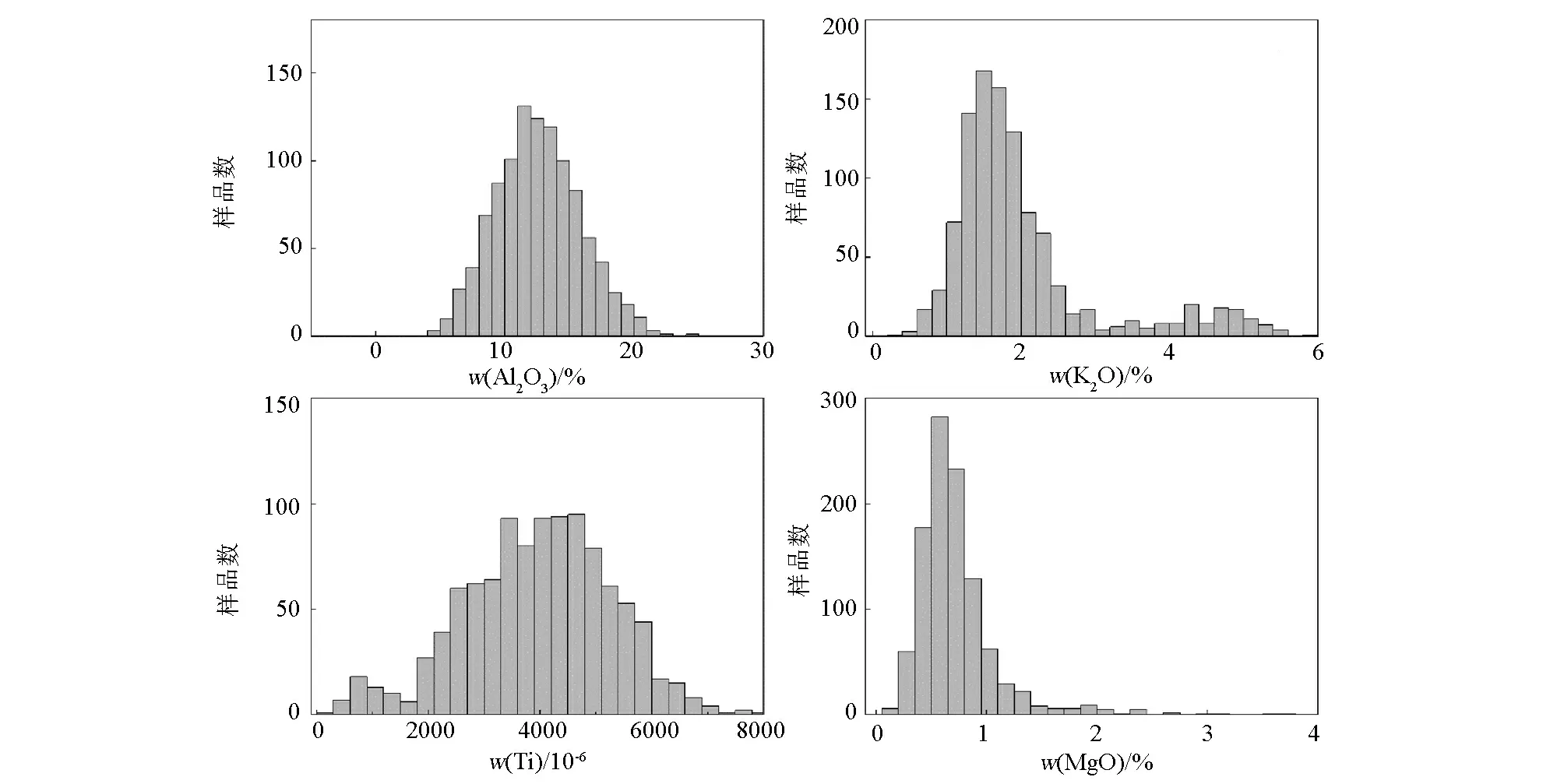
图2 水系沉积物样品Al2O3、K2O、Ti、MgO含量概率分布型式Fig.2 The frequency distributions of Al2O3,K2O, Ti and MgO of stream sediment samples

研究区岩性组成主要为灰岩、泥灰岩、砂岩和二长花岗岩等。岩性背景差异导致水系沉积物中元素含量的概率分布型式多呈偏态(图2)，如K2O和MgO均呈明显的右偏分布，Ti呈明显的左偏分布，且K2O和Ti还具有多峰分布特征；Al2O3虽然呈正态分布，但可能也是多个正态分布叠加的结果。为了合理地划分研究区水系沉积物地球化学背景与异常，需消除岩性背景差异的影响。

3.2 水系沉积物样品分类

首先，选择可以反映岩性变化，且元素间相关性较小的非成矿的常量和亲石微量元素作为分类指标。基于上述原则，本次实验共挑选出7种元素，即Mn、Ti、V、Zr、CaO、K2O和MgO，对其他受岩性影响较小的元素和成矿元素W、Sn则不予考虑。利用上述分类指标，通过EM算法对样品进行分类，分类过程主要在MATLAB中实现。

AIC值计算结果表明，随着分类数的增大，AIC值先是迅速减小，当分类数增大到一定程度后，AIC值的下降幅度变得越来越小，最后趋于平稳，即AIC曲线趋于水平(图3)。根据AIC判别原则，AIC值达到最小时可获得最优分类数，即分类数越多越好，可在最大程度上区分混合正态母体。然而，在分类过程中还需考虑实际情况，因为分类过细可能会使某些分类中的样品数过少而达不到基本统计要求。

观察发现，分类数8前后的AIC值变化幅度较大，因此可以考虑8及以上的分类数；在分类过程中，分类数达到8时部分类别中的样品数过少，甚至只有个位数样品；另外，研究区岩性组成相对简单，因此分类数不宜过大。基于上述理由，在分类数8的基础上将一些样品数过少的类合并到了附近的类中，最终将样品分为5类(图4)。由于EM算法在计算过程中容易出现局部最优解的情况，因此在每次分类过程中进行了多次重复计算。将分类结果成图，比较分类图与地质图(图1)的吻合程度，发现分类结果较为合理。整体上，分类界线与研究区主要地质单元界线吻合较好，但也存在同一地质单元内出现多种分类的现象，如图幅中部的上古生界灰岩、泥灰岩分布区出现了第1类和第3类样品，这是同一地质单元内具有不同岩性单元的真实反映。另外，还存在同一分类区域对应着不同地质单元的现象，如图幅中第4类样品分布区对应着白垩系砂岩、泥盆系砂岩和下古生界浅变质砂岩。总的来说，将水系沉积物样品分为5类较符合实际情况，其中，第1类样品对应灰岩，第2类样品对应燕山期二长花岗岩，第3类样品对应泥灰岩，第4类样品对应砂岩，第5类样品对应印支期二长花岗岩。

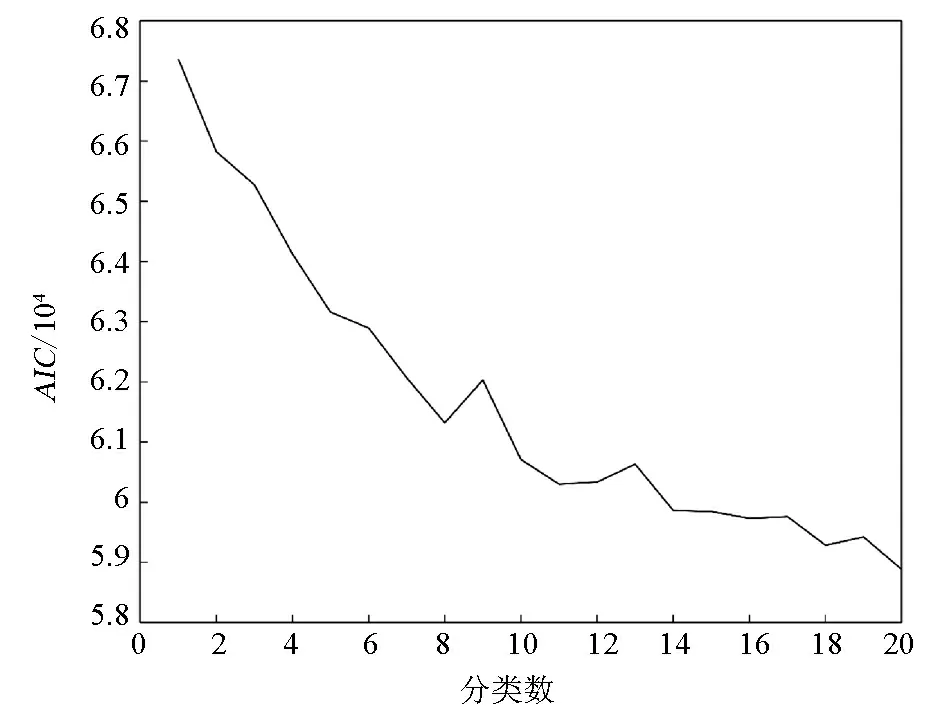
图3 分类数与AIC值关系曲线Fig.3 Relationship between number of clusters and AIC values

分类后绝大多数母体中的样品元素含量都服从(近似)正态分布(图5)，说明分解多重母体取得了较好的效果，在确定地球化学背景与异常的过程中可直接采用传统的均值加k倍标准偏差的方法。值得注意的是，某些区域内可能存在水系沉积物混合物，是由来自不同岩性背景区的水系沉积物混合形成的。研究表明，多重母体分解后，这些水系沉积物混合物中的多数元素含量仍不服从(近似)正态分布[5]。针对这种情况，目前还没有较好的处理方法。在这种情况下可作取对数、平方根、倒数等变换或直接当作正态分布处理，这是一个策略选择问题。

图4 分类结果Fig.4 Optimal classification map

图5 分类后Al2O3、K2O、Ti、MgO含量概率分布型式Fig.5 The frequency distributions of Al2O3,K2O, Ti and MgO of separated samples

3.3 异常圈定及效果评价

为了便于比较，笔者采用EM方法和传统的均值加k倍标准偏差的方法分别圈定了W和Sn的地球化学异常(图6)。由于W和Sn的概率分布型式为非正态，因此采用传统方法处理之前先对原始数据进行了对数变换，然后采用3S检验法对所有样品数据进行检验，剔除异常样品后再计算均值和标准偏差，以此进行Z分数标准化。数据标准化后，将背景上限确定为均值加2倍标准偏差，然后进行异常圈定。EM方法计算步骤为：对每个子类的样品数据先采用3S检验方法剔除异常样品，计算均值和标准偏差，然后对各子类中的数据进行标准化，以消除岩性背景差异的影响，合并标准化之后的各个子类数据按统一背景上限进行异常圈定。

结果表明，两种方法圈定的地球化学异常存在明显差异，消除岩性背景后圈定的异常无论从强度上还是形态上均发生了显著变化。总的来说，分类后圈定的W和Sn的异常与已知矿床(点)的位置对应关系更好，而常规方法圈定的异常有偏移现象。另外，本文方法圈定的异常强度得到了明显增强，不仅发现了一些传统方法没有发现的低弱异常，如B1、B2、B3、B4和B5，还消除了岩性背景高值区形成的虚假异常，如二长花岗岩分布区的A1和A2。这些虚假异常是由岩性背景造成的。统计发现，不同岩性分布区的元素背景值差异较大(表1)，砂岩分布区的元素背景值最低，其次是灰岩和泥灰岩分布区，而燕山期二长花岗岩分布区的元素背景值最高，印支期二长花岗岩次之，若全区统一进行异常圈定，显然会压低砂岩分布区的异常，放大二长花岗岩分布区的异常。

受岩性背景影响较大的W和Sn，两种方法圈定的异常差异较大。由于二长花岗岩分布区的元素背景值明显高于其他岩性分布区，因此传统方法圈定的W、Sn异常多位于二长花岗岩分布区，而在灰岩、泥灰岩及砂岩分布区几乎没有显示。相比较而言，本文方法消除了岩性背景差异的影响，圈定出的W、Sn异常主要分布于二长花岗岩岩体的周边，且在砂岩、灰岩及泥灰岩分布区也有显示。另外，本文方法圈定的异常规模也较大，强度也较高，与已知矿床(点)的对应关系更好，说明利用该方法圈定的异常更为合理。

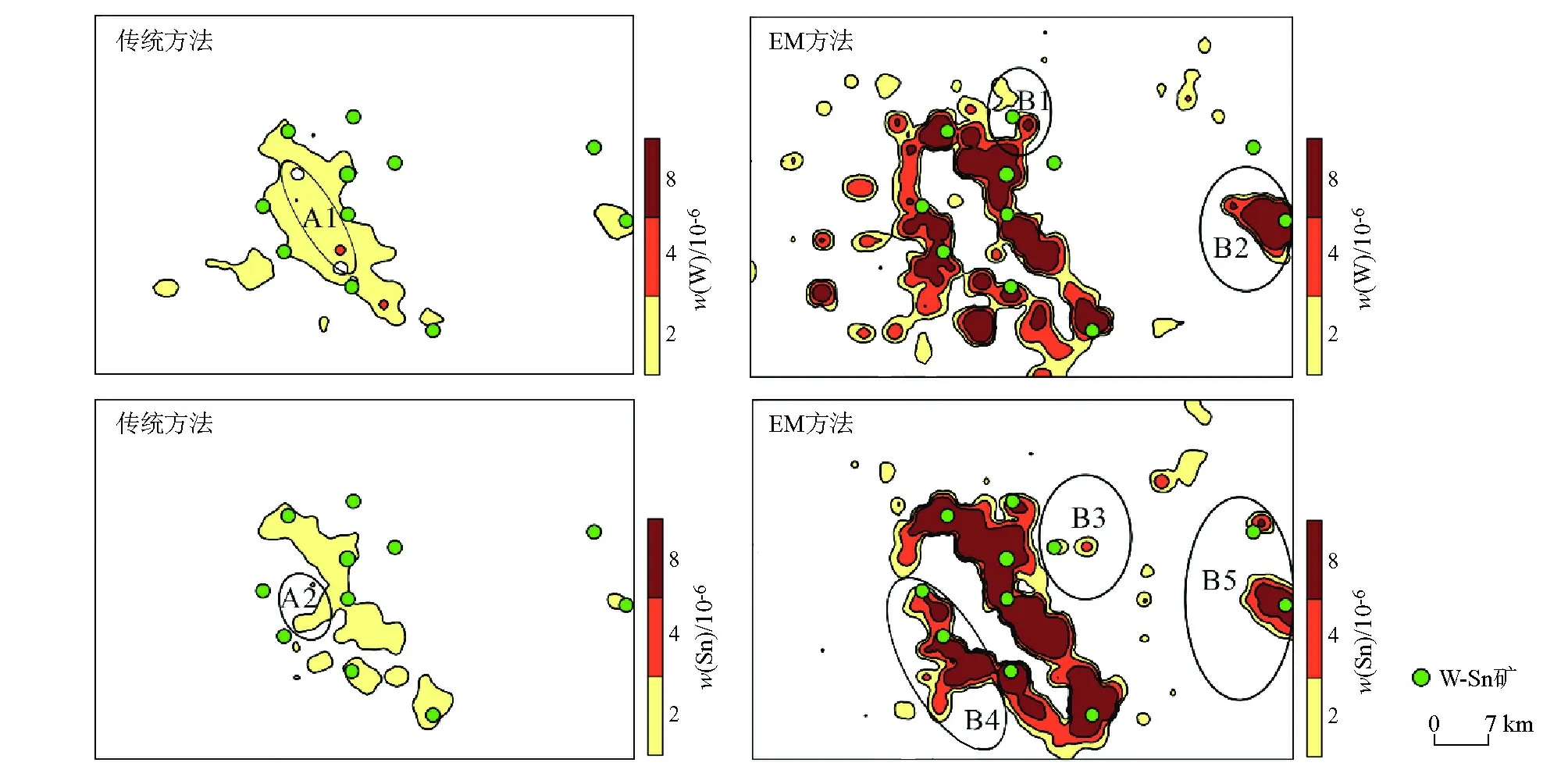
图6 传统方法(左侧)与EM方法(右侧)圈定的W、Sn地球化学异常Fig.6 Geochemical anomalies of W and Sn delineated by traditional method(left) and the EM method(right)

表1 分类样品中W、Sn背景值

4 结论

1) 采用EM分类方法能够快速、有效地区分来自不同岩性背景的水系沉积物样品，可在一定程度上消除岩性背景的影响。该方法以水系沉积物对基岩化学成分显著的继承性为基础，具有明确的地质意义。

2) 消除岩性背景影响后，不仅可以圈定出低弱地球化学异常，还可以削弱虚假地球化学异常。

3) 分类完成后，对各类样品元素含量进行正态分布检验，若服从(近似)正态分布，则可直接采用传统的均值加k倍标准偏差的方法或其他方法圈定地球化学异常，若不服从(近似)正态分布，则可作取对数、平方根、倒数等变换或直接当作正态分布处理，这是一个策略选择问题。