DEM网格间距对重力远区地改精度的影响及效果

李忠平，戴广凯，张茂辉

(1.中国地质大学(武汉) 地球物理与空间信息学院，湖北 武汉430074；2.中国冶金地质总局 山东正元地质勘查院，山东 济南 250014； 3.山东省地质调查院，山东 济南 250013； 4.中国海洋大学 工程学院，山东 青岛 266100)

0 引言

1∶5万重力远区地改原则上使用1∶5万卫星DEM数据(节点距25 m)，也可采用RGIS自带高程库进行远Ⅰ、Ⅱ区地改。由于RGIS自带高程库是基于“区域重力信息系统2006”自带1 km×1 km节点高程，网格间距偏大[1-3]。本次对山东省栖霞市臧家庄幅1∶5万重力观测数据采用以上两种网格节点的高程数据进行了远Ⅰ、Ⅱ区地改试验，以评价两种方法的合理性和可行性。

1∶5万重力勘查跨越了不同的DEM数据图幅，要获取有重力勘查边界的DEM数据区域时，必须对多个图幅的DEM数据进行拼接。由于数据拼接时插值方法不同，其数据拼接精度不同。为满足重力远Ⅰ区地改的需要，采用Suffer8双线性插值法快速进行DEM数据拼接，解决了该区地形高差较大时插值效果差等问题[4-6]，从而使高精度GPS因信号较差而采集的个别低精度高程点对应地改误差减小[7-9]，同时使用Suffer8可更加方便地自定义不同的网格间距进行DEM数据拼接，以满足不同的探测需求，解决了地形对重力观测异常的影响[10-12]。

试验使用Suffer8进行DEM数据网格拼接，然后用GeoIPAS3.0软件进行远Ⅰ区地形改正时，由于DEM数据网格间距不同，1∶5万重力远Ⅰ区(2～20 km)地改的速度不同，网格间距大，地形改正效率高[13-14]，对应地改均方误差大。实际工作时，采用RGIS自带高程库进行1∶5万重力远Ⅰ、Ⅱ区地改速度快，760个测点1～2 min即可完成。而采用GeoIPAS3.0软件进行远Ⅰ、Ⅱ区地改时760个测点一次完成要40 h(网格间距25 m)，数据处理效率较低。网格间距成为制约地改效率和精度、地质解释效果的主要因素[15-16]。为探索最佳网格间距，本文通过对山东省栖霞市臧家庄幅1∶5万重力远Ⅰ区地形改正数据分析，采用25、50、100、200 m四种网格节点距进行了1∶5万DEM数据拼接和对应重力远Ⅰ区地改、均方误差计算。将1∶5万卫星DEM数据节点距扩大一倍，即用50 m的网格距拼接，能较好满足地形改正效率与精度的要求，缩短了1∶5万重力远区地形改正时间，提高了资料整理效率，更有利于推断解释工作[17-19]。

将重力勘查数据与地质、遥感资料综合是发现深部隐伏断裂的重要手段[20]。而远区地改精度在重力地改中占有重要地位，它影响对地质和遥感资料的准确解释，对发现深大断裂和深部矿体意义重大[21]。由不同网格节点的DEM数据和RGIS自带高程库做地改后的精度对比，研究其对布格重力异常的影响，很容易被技术人员忽略。它会影响对局部重力异常的解释，有时会漏掉一些有意义的异常，从而错失找矿机会。

因此，在1∶5万重力勘查区地形较为复杂、布格重力异常总精度及地形改正均方误差要求较高时，首选1∶5万卫星DEM数据(节点距50 m)进行重力远区地改。在满足规范要求的情况下，也可采用RGIS自带高程库进行重力远区地改。经研究对比两种远区地改方法各有优缺点。对于大测区大数据量的重力远区地改，建议分区分幅进行，同时重视DEM数据拼接时网格间距的选择，避免重力远区地改耗时太长，降低工作效率。

1 重力远区地改方法

将以测点为中心的四周地形分割成许多小块，尽可能模拟实际地形。计算出每一小块地形质量对测点的重力值，再累加求和得出该点地形改正值。共用点法为其常用方法之一，共用点法是将实际地形分割成四棱柱体。首先计算重力测点(自由网点)附近4个节点的地形改正值(计算时用测点高程值代替四个节点的高程值)，然后再将4个节点的地形改正值内插到测点位置上作为测点地形改正值，计算公式为(1)[22]

(1)

式中：δg(x,y)为测点地形改正值；f为万有引力常数6.67×10-11m3/(kg·s2)；σ为地形校正密度；hij为节点与计算点的高程差；rij为节点与计算点的距离；Δx、Δy为网格距或节点距；Cij为积分常数，此处选用梯形系数Cij：

由上式可知，测点重力地形改正值δg(x,y)与网格距或节点距Δx、Δy有关，网格距或节点距选择合适与否，决定了重力远区地改的精度高低[22-23]。

计算测点附近的4个节点的测点重力值后，采用双线性插值公式计算出测点重力数据的远区改正值(图1)。

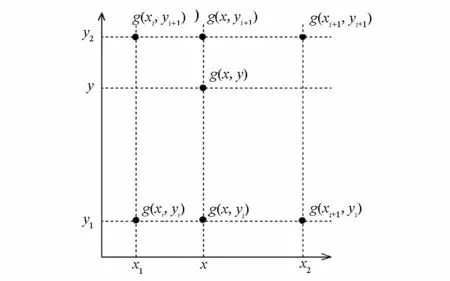
图1 双线性插值法图示Fig.1 Bilinear Interpolation Graphics

双线性插值计算公式如下：

(2)

(3)

(4)

式中：g(x,y)为地改值双线性插值结果；g(xi,yi)、g(xi,yi+1)、g(xi+1,yi)、g(xi+1,yi+1)为4个节点的地改值；xi、xi+1、yi、yi+1为节点坐标值；Δx、Δy为节点距。

由上式可知，测点重力地形改正值δg(x,y)精度及地改速度受网格距和边缘方向插值算法的制约，为解决这一问题，本文提出对双线性插值法进行改进。

2 改进的双线性插值重力远区地改计算方法

针对传统的双线性插值在实现沿任意边缘方向插值时图像边缘模糊及算法速度、精度问题，本次研究对双线性插值法进行改进，基于边缘方向的插值是一种有效图像插值方法。 双线性插值沿水平和垂直两个方向进行插值，不利于图像的实时放大处理，或难以达到最佳效果。本文提出首先确定插值点的重力值和边缘方向，再引入双线性插值算法，沿边缘方向进行插值，有效地提高了插值图像边缘的清晰度及算法速度、地改精度[24-25]。

如图2所示，g(xi,yi)、g(xi,yi+1)、g(xi+1,yi)、g(xi+1,yi+1)为4个节点的地改值，O点为位于非正交直线AB上的待求内插点，非正交直线4个节点所构成的四边形非垂直相交。

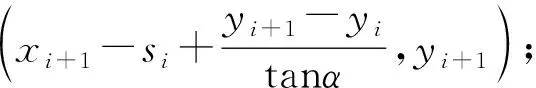
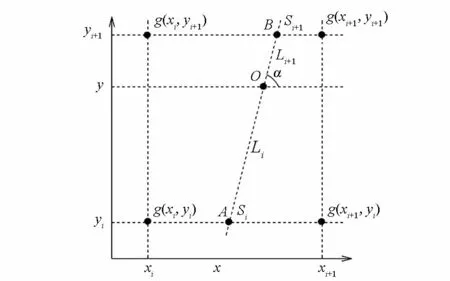
图2 改进的双线性插值法图示Fig.2 Improved bilinear interpolation method

由A点在g(xi,yi)、g(xi+1,yi)之间进行线性插值得到A点的地改值公式为：

(5)

由B点在g(xi,yi+1)、g(xi+1,yi+1)之间进行线性插值得到B点的地改值公式为：

(6)

由O点在A、B之间进行线性插值得到O点的地改值公式为：

(7)

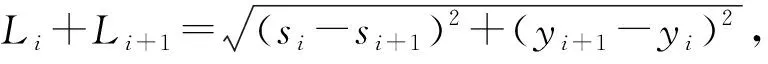
使用matlab编程实现改进的双线性插值法，并进行了重力远区地改值计算。

在测区西南角选择了4个重力观测点(节点)(图3)，改进的双线性插值法4节点编号分别为g(xi,yi)、g(xi,yi+1)、g(xi+1,yi)、g(xi+1,yi+1)，其坐标见表1。依据图3，取si=2 000 m，si+1=1 000 m，α=45°。

由图3可知，在测区西南角，Δg一般在(-15～-10)×10-5m/s2之间变化，因此改进的双线性插值法较好反映了重力异常的变化趋势，可以提高推断解释的精度。

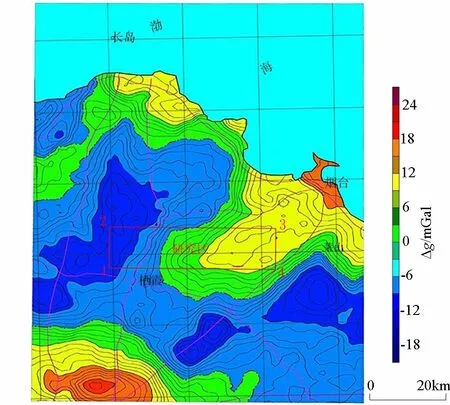
图3 山东烟台地区区域布格重力异常平面Fig.3 Plane of Bouguer gravity anomaly in the Yantai area of Shandong Province

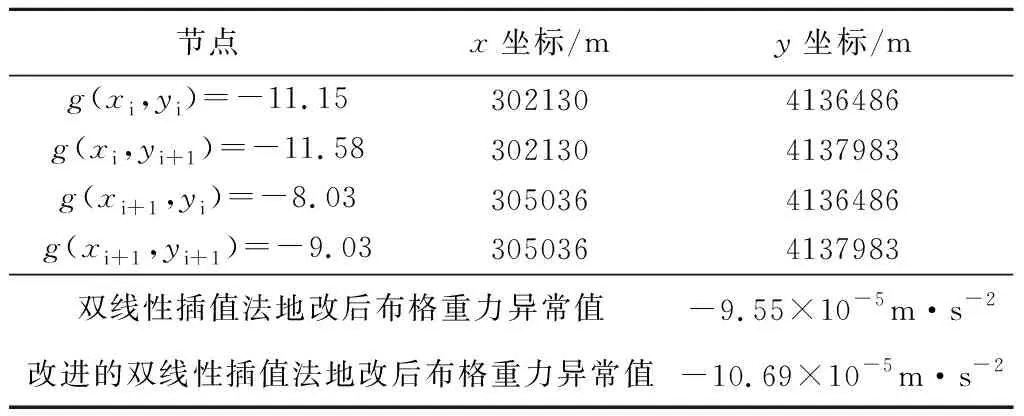
表1 改进的双线性插值法试验计算对比

3 重力远区地改精度对比分析

1∶5万卫星DEM数据原始节点距为25 m，基于该节点距的山东省栖霞市臧家庄幅1∶5万重力勘查DEM数据网格拼接用于重力远区地改存在效率较低的事实。本次选取该区27个测点原始与检查数据，在使用Suffer8进行DEM数据拼接时选取了25、50、100、200 m四种网格节点距，使用金维GeoIPAS3.0软件将原始与检查数据分别进行了重力远Ⅰ区(2～20 km)地改试验。地改精度与时效指标情况见表2。由表2可知，网格节点距越大，重力远Ⅰ区(2～20 km)地改时间越短，地改均方误差越大。经试算，该区合适的网格节点距为50 m，其重力远Ⅰ区地改均方误差为0.000 36，优于使用RGIS自带高程库重力远Ⅰ区地形改正均方误差(0.03),满足规范要求。

对山东省栖霞市臧家庄幅1∶5万重力勘查760测点采用25 m×25 m网格节点距DEM拼接数据。金维GeoIPAS3.0软件进行了重力远Ⅰ、Ⅱ区地形改正，760个测点一次地改需要42 h。可见25 m×25 m网格节点距DEM数据用于地改效率较低。

表2 不同网格间距重力远Ⅰ区地改精度统计

4 应用效果对比

4.1 重力异常特征对比

研究区为山东栖霞臧家庄盆地，区内岩浆岩分布广泛，以中生代郭家岭序列罗家单元斑状中细粒含黑云二长花岗岩为主。玲珑—招风顶脉岩带通过该区，脉体产状为：走向20°～40°，倾向NW向为主，SE向次之，单脉宽2～50 m，长度多在1 100～8 000 m。岩石类型有煌斑岩、闪长玢岩、石英闪长玢岩、石英正长斑岩、细晶闪长岩等。臧家庄盆地西缘紫现头断裂和北缘西林断裂交汇于本区，构造复杂，次级断裂众多。区内NE向断裂构造较发育，且多以张性为主，与金矿关系密切。

研究区区域重力异常特征：区内重力场值西北低，东南高(图3)，变化范围为(-14～14)×10-5m/s2，异常等值线主要呈现NNE向展布，并叠加一些局部重力异常。重力场特征为密集的重力异常梯级带。根据区域地质资料推断为典型的深大断裂的反映。在其西北部区域，重力梯级带变得宽缓，局部区段扭动频率增强，说明局部构造发育，但重力场构造线总体为NNE，与地质构造格架吻合。

研究区地形特点：在研究区西部和中东部均有2处相对较高地形(图4)，高程一般在111～316 m。全区最高点在东部，高程360 m；最低点在东北角，高程70 m，全区地形高差为290 m。这些相对较高地形为山区，中部和东部共有3条带状相对低值地形区，为山沟和第四系。

研究区已知矿床地质特征：该区内已知的矿产主要是金矿，其中小型矿床1处，矿点2处，矿化点1处。郭家店小型金矿，赋存于NE向张性破碎带中，产于一组NE向的石英脉中。成矿时代为燕山期，围岩为斑状中粒花岗闪长岩，主要蚀变为黄铁矿化、绢云母化、褐铁矿化等，化学分析金含量在(3～10)×10-6之间(图5)。

研究区重力异常特征：重力异常总体走向为NE向。重力场表现为东高西低特征，局部稍有变化。低值区位于工作区西北角，布格重力异常值一般在(-14～0)×10-5m/s2之间变化，与二长花岗岩和古元古界粉子山群祝家夼组透闪大理岩和变粒岩对应；高值区位于工作区东北部，布格重力异常值一般在(0～15)×10-5m/s2之间变化，与二长花岗岩和石英闪长玢岩脉对应(图5、图6)。

研究区已知金矿脉的重力异常特征：西北部3条和西南、中南部9条金矿脉均处在布格异常等值线梯级带和扭曲变形之处，布格重力异常值一般在(-13～5)×10-5m/s2之间变化，属相对低缓布格重力异常(图1、图6)。

图6与图7是分别基于RGIS自带高程库(网格距1 km)和基于DEM(网格距50 m)改进的双线性插值中远区地改后布格重力异常分布特征。二者布格重力异常展布形态基本相同，只在基于RGIS自带高程库中远区地改后布格重力异常图的北东部有两处重力高值异常与基于DEM改进的双线性插值中远区地改后布格重力异常稍有不同，在图7中两处重力高值异常消失，显示为正重力异常梯级带，提高了地质解释的精度。产生这一差别的原因与这两处高差变化之大有关， 是RGIS自带高程库的网格距远大于DEM网格距所致。

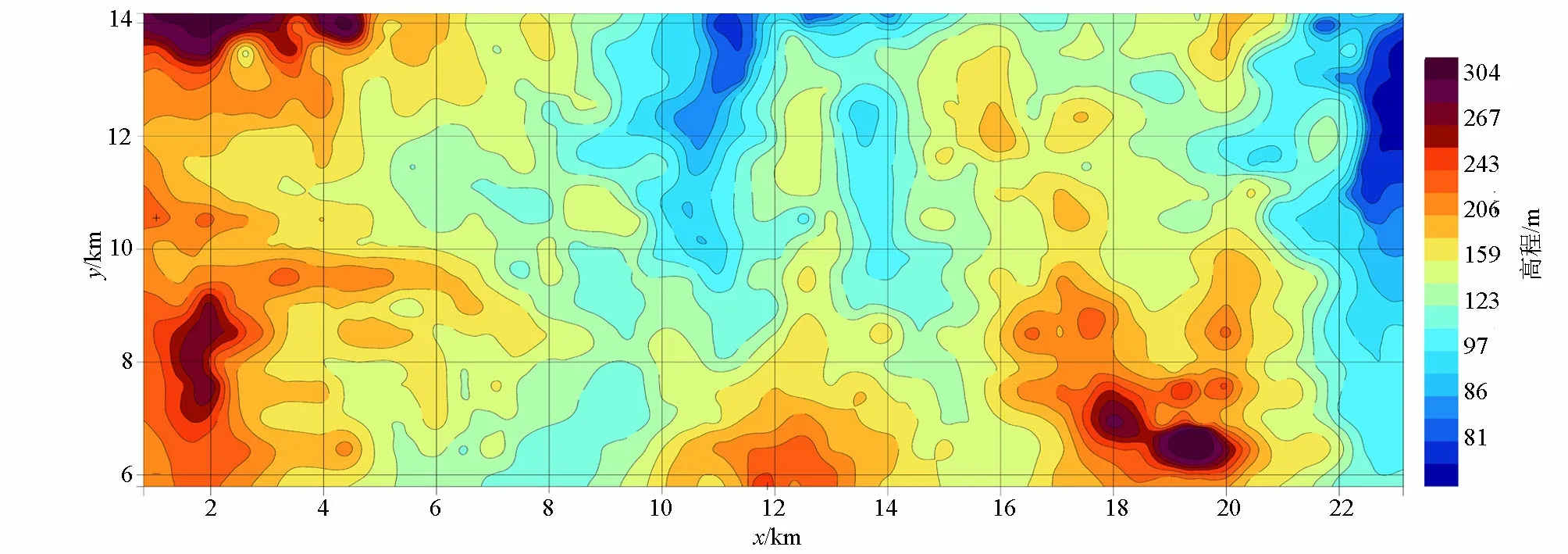
图4 研究区地形Fig.4 Topographic map of the study area

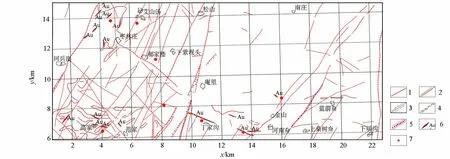
1—推测断裂; 2—压扭性断裂; 3—张性断裂; 4—韧性断层; 5—构造破碎带; 6—金矿脉; 7—钻孔1—speculated fracture; 2—compression torsion fracture; 3—tensile fracture; 4—ductile fault; 5—structural fracture zone; 6—gold vein vein; 7—drilling图5 研究区构造及矿点分布Fig.5 Structure of the study area and Titanium Vein

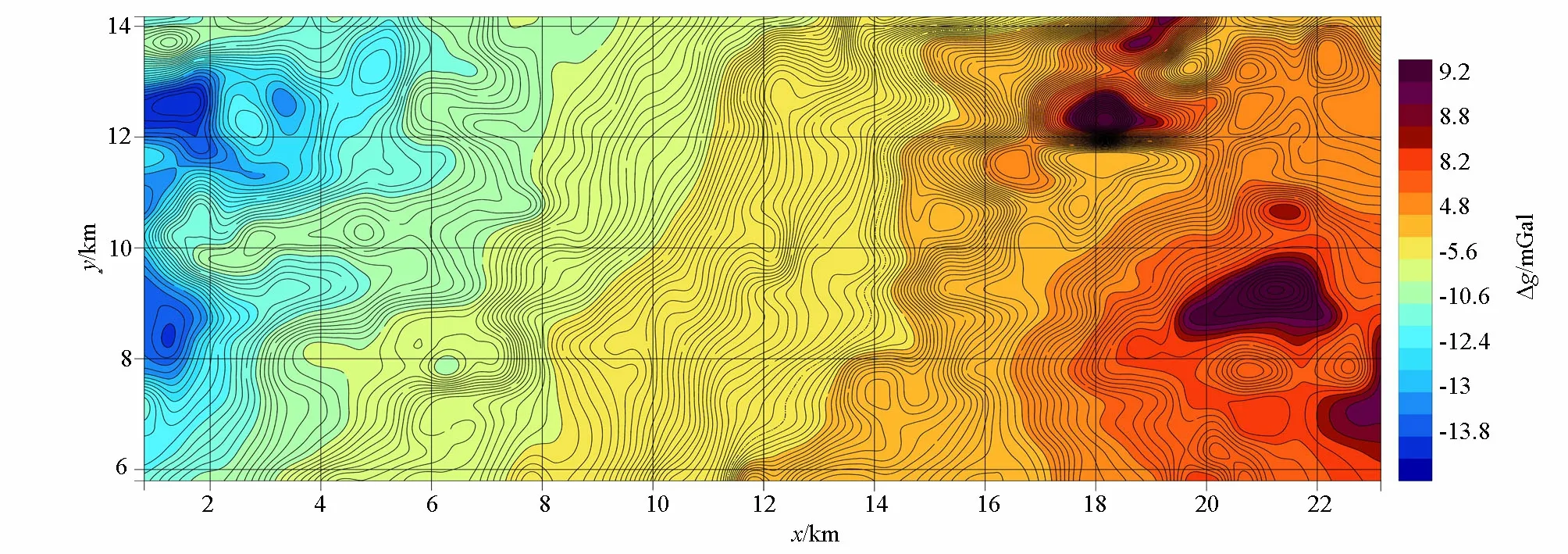
图6 基于RGIS自带高程库中远区地改后布格重力异常Fig.6 Based on the Bouguer gravity anomaly map of the remote area of RGIS with its own elevation

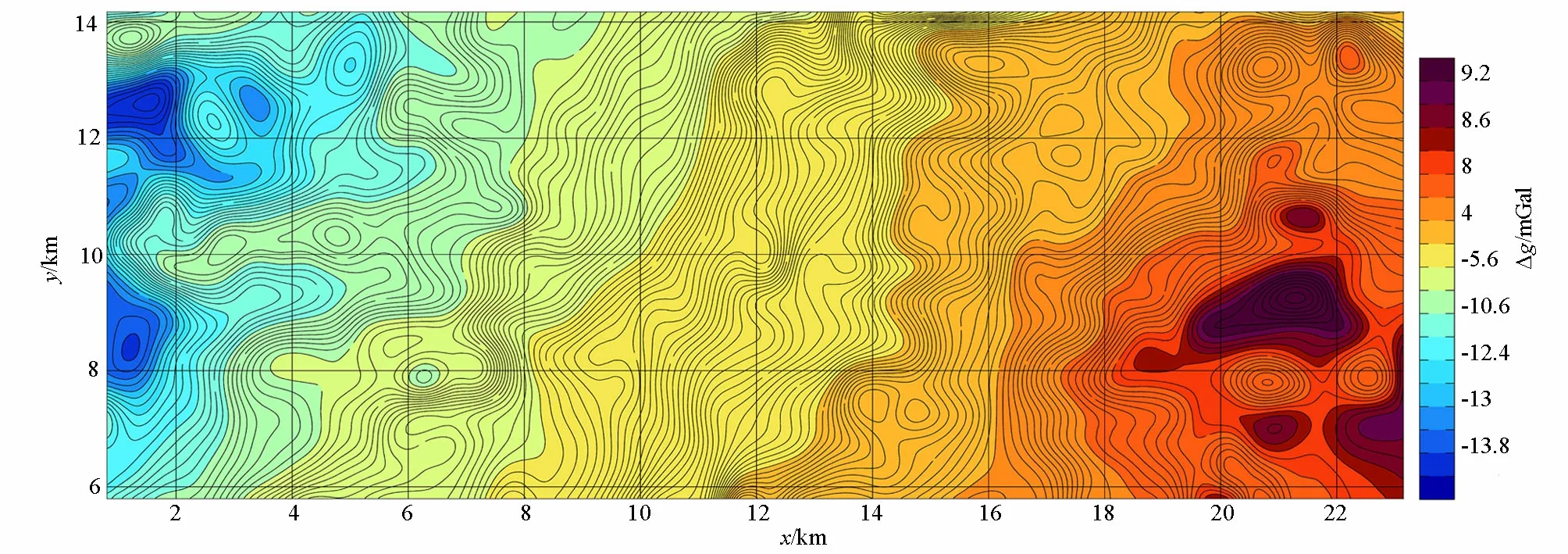
图7 基于DEM改进的双线性插值中远区地改后布格重力异常Fig.7 Modified Bouguer gravity anomaly map of far area by bilinear interpolation based on DEM

研究区构造特征：布格重力高异常等值线密集、梯度变化较大及错断部位，是推断深大断裂的依据。区内具多个圈闭中心的异常，表明局部构造发育。位于研究区西部摩天岭—南交毛寨—艾山汤一带断裂，异常呈梯级带和扭曲收缩特征，沿NE向展布，布格重力异常值在-11×10-5m/s2左右；位于研究区西部高家—盛家—疃顶一带断裂，异常呈梯级带和扭曲收缩特征，沿NE向展布，布格重力异常值在-10×10-5m/s2左右(图5、图7)。

4.2 重力异常相关分析

研究区的地形变化对重力异常的影响不容忽视，无论地形的隆起或是凹陷，都将减小异常的实测值导致重力异常图在形态上的直接变化，影响对异常的客观解释。将布格重力异常和地形两个物理量进行相关分析，以反映研究区内地形起伏对重力异常的影响情况，以及地形改正是否完全或改算方法是否完善。重力异常和地形之间的相关分析依据式(8)[27]：

(8)

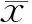
图8、图9分别为基于RGIS自带高程库(网格距1 km)和DEM(网格距50 m)改进的双线性插值中远区地改后布格重力异常和高程相关系数分布特征。图8的北东部有两处相关系数与图9的不同，在图9中这两处相关系数明显增大，并且连续。产生这一差别的原因亦与该处高差变化之大有关，是RGIS自带高程库的网格距远大于DEM网格距所致，说明基于DEM改进的双线性插值远区地改完全度高于基于RGIS自带高程库远区地改，并且改算方法精度较高。

5 结论与讨论

本次试验重力远区地改精度以均方误差体现。经对比分析：基于1∶5万卫星DEM数据50 m×50 m网格节点距的1∶5万重力远区地改精度优于使用RGIS自带高程库(网格距1 km)重力远Ⅰ区地形改正精度。在不同地形和不同精度要求的测区可选择使用以上两种方法。该试验证明：对重力远区地改不能完全以DEM数据中默认网格节点距为准，要通过DEM数据不同网格节点距试算重力远区地改值。改进的双线性插值法计算远区地改值证明，该方法提高了算法速度和精度。

研究结果表明，基于DEM改进的双线性插值法远区地改布格重力异常和高程相关度更高，对线性构造和地层、岩体的边界的识别精度高。从本区的布格重力异常图对比中发现：随着基于DEM改进的双线性插值法地改不同网格距的选择和高差变大，异常局部会产生不同的形态变化，从而提高地质解释的精度，这是值得注意的一点。

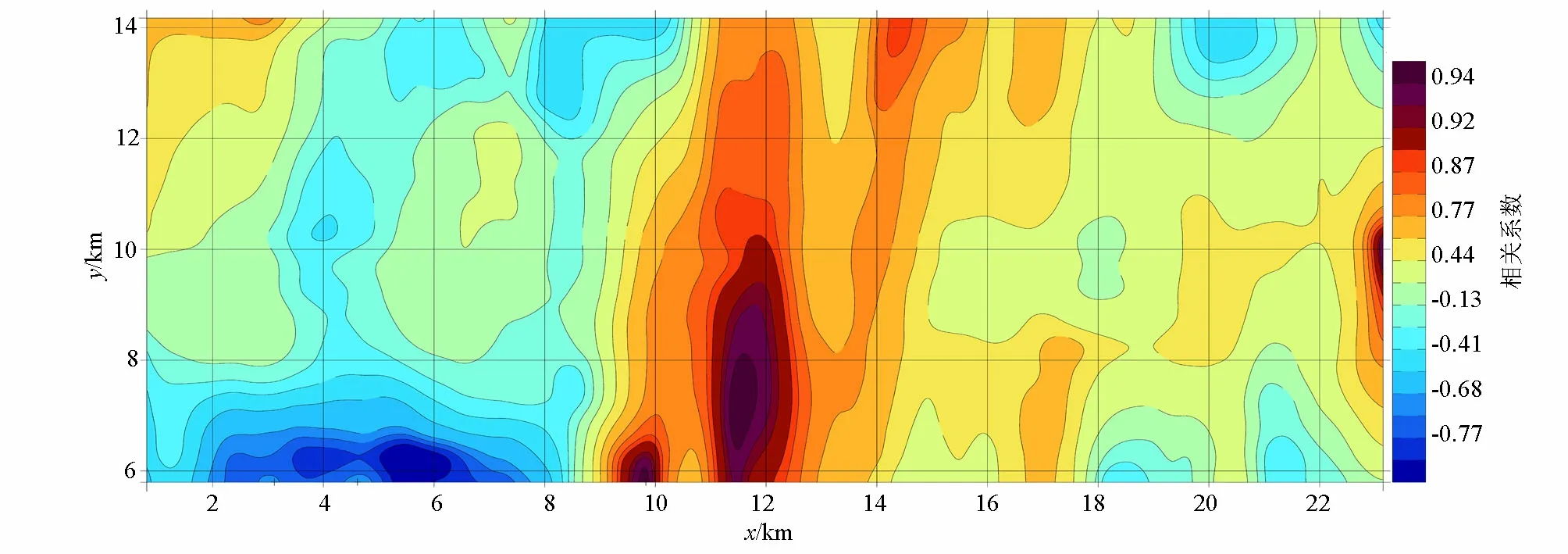
图8 基于RGIS自带高程库布格重力异常和高程相关系数分布Fig.8 Based on the distribution of elevation kupger gravity anomaly and elevation correlation coefficient in RGIS

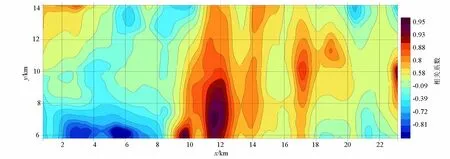
图9 基于DEM改进的双线性插值布格重力异常和高程相关系数分布Fig.9 Improved bilinear interpolation kupger gravity anomaly and elevation correlation coefficient distribution based on DEM