基于多时间尺度需求侧响应模型的网损优化方法

况 华，沐欣欣，覃日升

(1.云南电网有限责任公司，云南 昆明 650011；2.云南电网公司玉溪供电局，云南 玉溪 653100；3.云南电网有限责任公司电力科学研究院，云南 昆明 650217)

0 引 言

新电改9号文中提出“管住中间，放开两头”的电力运营模式，使得需求侧响应有更大的实施空间。需求侧响应对电能的供需平衡、电网的潮流特性会造成巨大的影响，同时也会影响到配电网的经济运行水平和网损特性[1]，因此利用需求侧响应来提高和优化配电网经济运行水平、降低电网网损已成为人们关注的热点问题。

目前国内外许多专家对网损优化做了相关研究。文献[2-7]分析了线路损耗的造成原因、计算方法以及优化网损的建议。关于优化网损方面，现有文献[8-16]基于设备改造、电网改造、线损率、交直流输电、安全经济调度、中低压电网等方面进行了研究。文献[8-9]考虑了设备改造，其中文献[8]通过确定电容器的位置及其类型和大小，升高线路电压，达到降低损耗的目的；文献[9]分析了变压器和导线的优化配置方法来实现降损的目的。文献[10]通过合理改变电网的运行方式，优化了电网的网架结构，提高了电网供电可靠性，达到节能降损的目的。文献[11-12]考虑了线损率，其中文献[11]提出一种基于极限线损率和极限降损率指标的配电网降损措施优化方法；文献[12]以线损二项式为分析工具，分析了过网电量、功率因数变化以及供电量增长等因素对线损率的影响，提出降损的方案。文献[13]提出了交直流混合电网的网损优化模型，利用拉格朗日乘子对优化模型进行求解。文献[14]提出了电力系统安全经济调度的网损协调优化方法。文献[15]分析了配电网降损规划工作的主要流程，并提出了配电网降损规划辅助决策模型。现有文献都能有效地降低网损，但很少有文献从需求侧响应的角度进行网损优化研究。仅有文献[16]在电力市场环境下，考虑需求侧响应建立了峰谷分时电价模型，达到网损优化的目标；但是其峰谷分时电价模型仅考虑了短期需求响应特性。

因此提出了新电改背景下[17]基于多时间尺度需求侧响应模型的网损优化方法。首先，对中长期需求响应特性及短期需求响应特性进行研究，建立了多时间尺度需求侧响应模型。该模型是在分时电价的需求弹性量化模型的基础上，通过同时考虑短期电价和中长期电价对需求侧响应的影响，能够反应出中长期电价波动情况下的短期需求响应特性。然后，从经济性角度出发，以网络损耗造成的经济损失最小为目标，将不同时段的网损分别乘上各自时段的电价，可以得到损失的电费，并以此最小为目标函数。最后以IEEE 30节点进行仿真分析，验证了所提方法的有效性。

1 多时间尺度需求侧响应建模

1.1 需求侧响应特性分析

1.1.1 中长期需求侧响应特性分析

中长期需求特性一般是以年为单位，时间跨度在几年到十几年之间。

中长期需求模型为

Inq=0.601Iny-8Inp+0.877InS+2000

(1)

式中：y为人均可支配收入；p为长期电价；S为人均居民住宅面积；q为年均电力需求量。

根据式(1)，分别取4组人均可支配收入和人均居民住宅面积的参数，如表1所示。

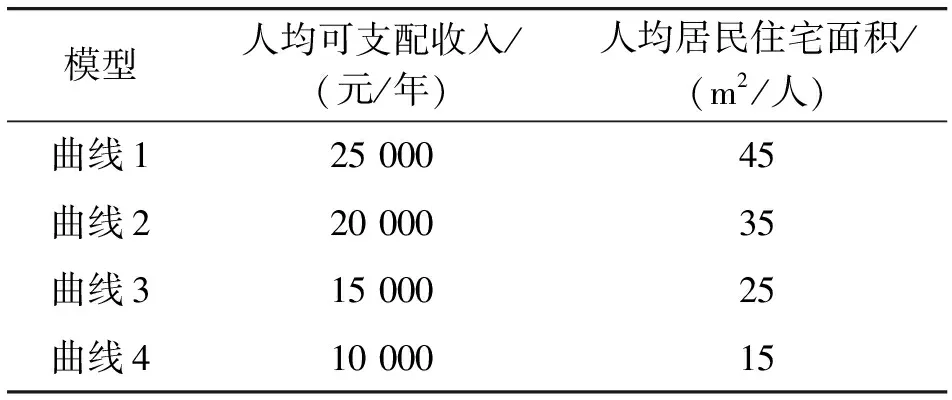
表1 参数设置

根据表1设置的参数，得到了中长期电力需求量与中长期电价之间的关系，如图1所示。

图1 中长期电量电价关系

1.1.2 短期需求响应特性分析

在短期电量电价的模型[18-19]中，可以引入负荷转移率的概念。负荷转移率的含义是用电需求高的时段向用电需求低的时段转移的用电量，与用电需求高的时段的用电量之比，得到短期需求模型如式(2)。

(2)

式中：λij为j时段的电价变化后，引起了i时段需求量的变化；pj为j时段的电价；p为常量，指代的是电价；K为用户反应度模型的斜率；A为死区阈值；B为饱和区阈值。

将分时电价分为峰、平、谷3个时段，得到9个相关的短期电量电价模型如式(3)至式(11)所示，式中的p暂时都取值0.5，(pj-p)/p(下标j分别用代表峰、平、谷时段的f,p,g表示)的范围设置为0～1。

(3)

(4)

(5)

(6)

(7)

(8)

(9)

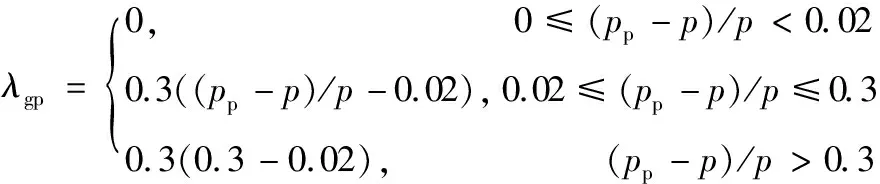
(10)

(11)

1.2 多时间尺度需求响应模型

多时间尺度需求响应模型如图2所示。

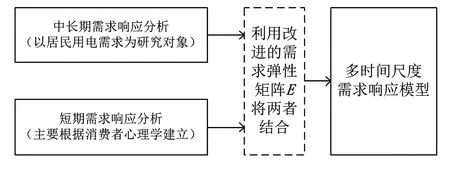
图2 模型结构

需求弹性矩阵中需求弹性系数可以表示为

(12)

式中：εij为需求弹性系数；Δqi/q为i时段需求量变化率；Δpj/pj为j时段电价变化率。当i=j时，εij为自弹性系数，即同一时段在分时电价前后的需求量变化，这一部分变化的负荷也可以称作可削减负荷，人们可能随着电价的提高而避免这部分负荷，达到减少电费支出的目的。当i≠j时，εij代表互弹性系数，即j时段的电价变化与i时段需求量变化之比，这一部分负荷也可以称作可转移符合，人们可能随着j时段电价的降低，减少i时段的用电量，并将这部分电量转移到j时段。

需求弹性矩阵为

(13)

式中：对角线元素为自弹性系数；非对角线元素为互弹性系数。

则多时间尺度需求侧响应模型为

(14)

式中：qDR=[qf-DRqp-DRqg-DR]T；qf-DR、qp-DR、qg-DR为需求侧响应执行后各时段用电量；qf、qp、qg为实施前各时段用电量。

按照峰、平、谷3个时段，可以得到：

(15)

结合式(3)至式(11)可以计算εij(i=f,p,g;j=f,p,g)的值。

2 网损优化模型

2.1 目标函数

电能在传输过程中由于线路的阻抗不可避免地会发生损耗，这部分损耗没有带来任何效益，却带来了巨大的经济损失。需求侧响应会通过改变电力网络中各个负荷输入的有功功率，从而改变网损结果以达到经济损失较少的目的。这里通过需求侧响应改变了用户的用电量，相当于改变网络中的功率分布，最终达到经济损失减少的目的。

优化网损的目标是使得网络损耗造成的经济损失最小，因此将不同时段的网损分别乘上各自时段的电价，可以得到损失的电费，将这个值取最小即是优化目标。函数表达式为

(16)

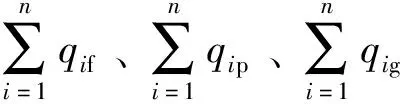
2.2 优化变量

基于以网络损耗造成的经济损失最小为目标函数的优化模型有4个优化变量，即[pf，pp，pg，p]。

峰价pf大于长期电价，它的增大会导致峰时段的负荷降低，同时使得平时段、谷时段的需求量增加，它与长期电价差值越大，峰时段负荷降低，平、谷时段负荷增加量越明显。

平价pp如果大于p会导致峰时段、谷时段需求量的增加；如果小于p则会引起峰时段、谷时段的需求量降低。一般不会与长期电价相差太多。

谷价pg小于长期电价，它的减小会导致峰时段负荷、平时段需求量降低，谷时段需求量提高，它与p的差值越大，则这些需求量的变化越大。

改变长期电价p则会引起一天中电力需求总量的变化，并且p与另外3个电价的差值也影响了最终各时段的需求量，因此p在该模型中有很大的影响。

2.3 约束条件

电价约束：

(17)

初始价格约束：

(18)

需求量约束：

(19)

需求侧响应约束：

qf-DR×pf+qp-DR×pp+qg-DR×pg≤q×p

(20)

还需要增加一些潮流计算时保证电力系统正常运行的约束条件：

1)所有节点电压的约束

Uimin≤Ui≤Uimax(i=1,2,…,n)

(21)

2)所有电源节点的有功功率和无功功率约束

(22)

PQ节点的有功功率和无功功率已经按照条件给定，PV节点的有功功率、平衡节点的有功功率和无功功率都需要满足上述条件。

3)有些节点之间的电压还需要满足相位要求

|δi-δj|<|δi-δj|max

(23)

有些线路两端的电压相位差必须要在一定范围内，这样可以保证系统稳定运行。潮流计算如果不能满足上述要求，则需要修改一些参数或者运行方式，重新计算。

2.4 求解算法

求解算法种类众多，但都有各自的优点和缺点，目前还没有完美的算法，考虑到高速计算的同时又能获取高精度的最优解，选择了粒子群算法作为优化算法[20]。通过粒子群算法来优化需求侧响应后得到的用电量，所得的用电量作为潮流计算的输入，再用MATpower进行潮流计算[21]，求出各节点的总净注入功率来表示网损。

网损优化模型的具体流程如图3所示。

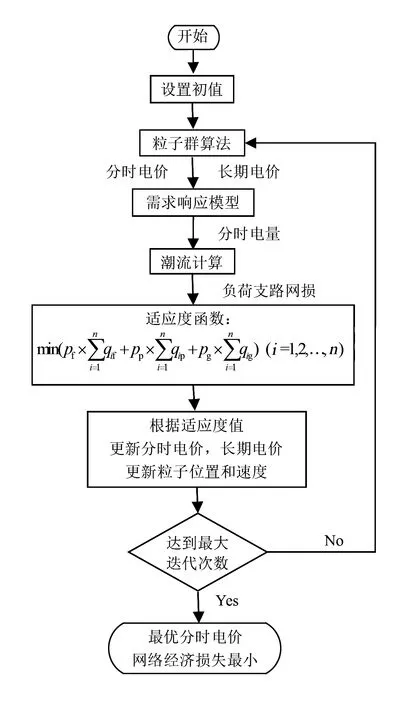
图3 网损优化模型的流程

3 算例分析

3.1 参数设置

峰、平、谷时段初始用电量设置如表2所示。

表2 需求侧响应参数设置

人均用电量q是通过中长期需求模型的函数表达式计算得出的，这是一年中的平均用电量，要计算一天中的用电量只需要将q除以365。进行网损优化时，将IEEE 30节点配电网中的一部分节点用需求侧响应求出的用电量来代替，由于电量和功率单位不同，这里需要稍作转换。由于默认每个时段为8 h，只需要将电量的值除以8就可以得到按小时计算的功率，并假设每个节点承担了80位居民的负荷，这样在计算某时段网损时，每个节点的负荷就是10倍的此时段用电量。

对粒子群算法的参数设置如表3所示。

表3 粒子群算法参数设置

将所提网损优化应用于IEEE 30节点系统，系统总的负荷为2.834+j1.390(标幺值)。基准功率为100 MVA。IEEE 30节点系统包括6台发电机(节点1，2，5，8，11和13，其中节点1为平衡节点，节点2，5，8，11和13为PV节点)、21个负荷节点、37条线路，4台可调变压器(支路6—9、6—10、4—12和27—28)和2个无功补偿点(节点10和24)。图4是IEEE 30节点配电网结构图。

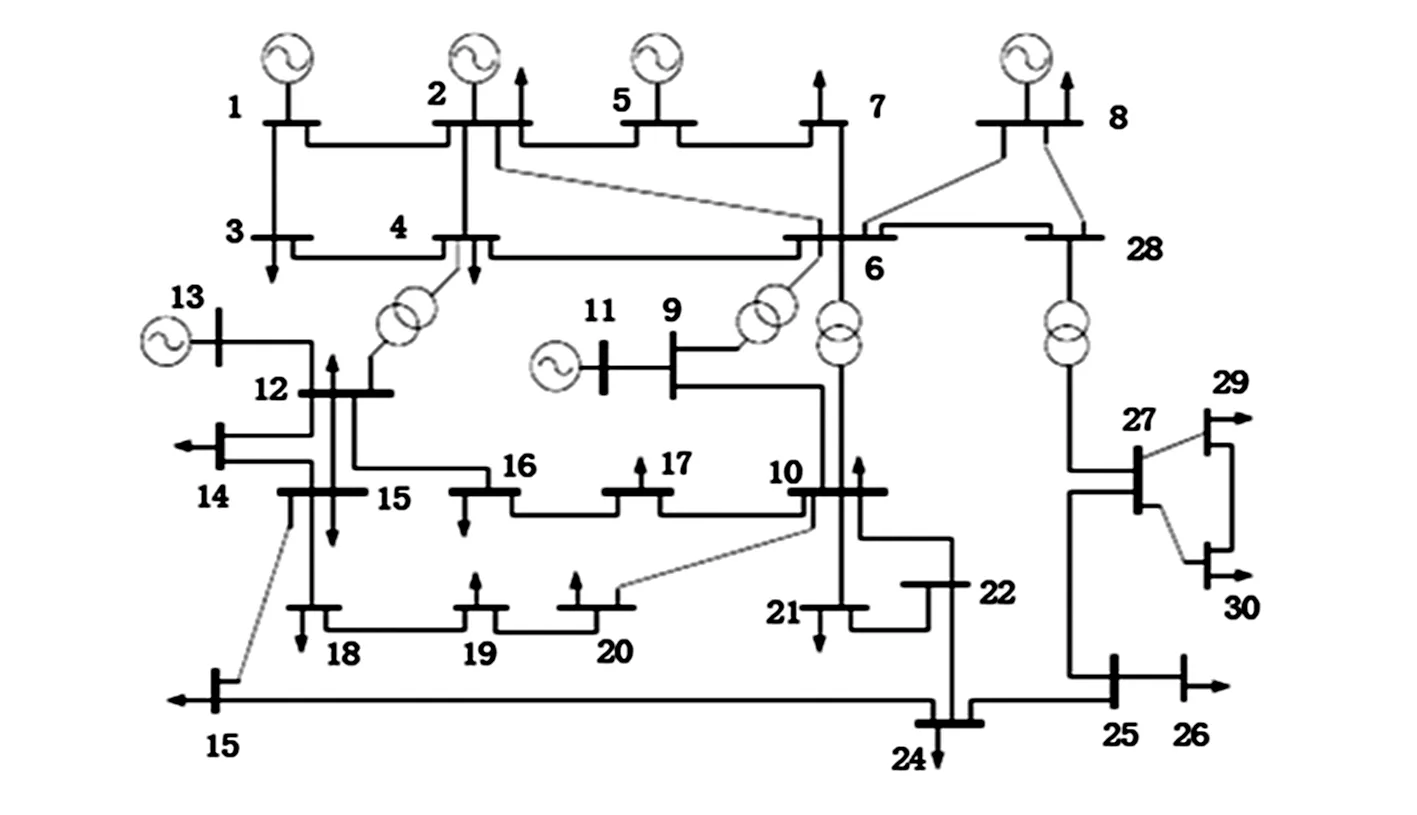
图4 IEEE 30节点配电网结构

3.2 结果分析

网损优化后得到的结果如下：

1)需求弹性矩阵

(24)

2)电价

网损优化后的电价如表4所示。

表4 网损优化后的电价 单位：元/kWh

表4中的数据显示峰价有所上升，但上升不多，原因在于本次优化将电价作为目标函数的一个因子，峰价受到了约束。平价略有下降，谷价下降较多，与预期一致。

3)优化过程

从图5的优化过程可以看到粒子群算法的寻优过程，迭代过程中出现过不同的局部最优值，最终找到了全局最优，经过800次左右的优化，数值从68.34降低到58.15，实现了预期的目标。表明该模型对降低网损造成的经济损失有效，符合预期。

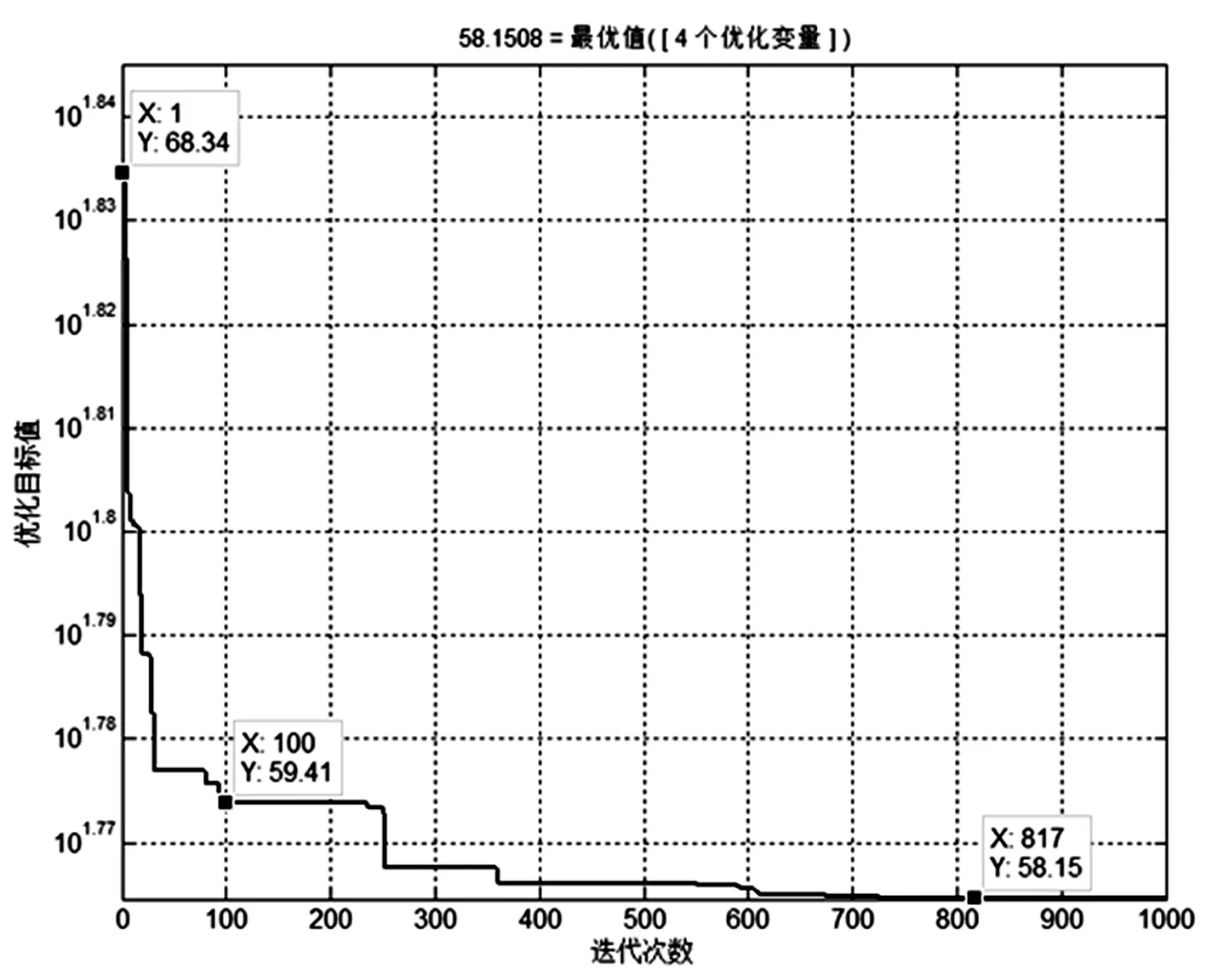
图5 粒子群算法优化过程

4)优化结果比较

实施网损优化前后电量、电费以及经济损失的比较如表5、表6、表7所示。

表5 网损优化前后电量比较 单位：kWh

表6 网损优化前后电费比较 单位：元

表7 网损优化前后经济损失比较

对基于网损优化的多时间尺度需求侧响应模型进行仿真后，可以看出峰谷差负荷由原先的1.747 kWh优化到1.107 kWh，总负荷量基本不变。平时段负荷减少了0.053 kWh，变化不大；峰时段负荷减少了0.346 kWh，减少较多；谷时段负荷增加了0.294 kWh，增加较多，表明所提出的模型能有效地将负荷由峰时段转移到谷时段。

电费方面，平时段电价下降了0.277元；谷时段电价下降了0.444元；峰时段电价上升了0.023元，峰时段变化不大，平时段、谷时段都有下降，且总电费下降明显，这能够提升居民的满意度。

网损方面，峰时段网损下降了21.258 kWh；平时段上升了2.263 kWh；谷时段上升了6.308 kWh；总的网损下降了9.3%，网损造成的经济损失也下降了19.8%，表明基于网损优化的多时间尺度需求侧响应模型能有效地降低网损，同时减少了网损造成的经济损失。

4 结 语

所提网损优化建模考虑了消费者心理学，并将长期需求模型与短期需求模型通过需求弹性矩阵结合在一起，建立了基于多时间尺度需求侧响应模型的网损优化方法。所提出的基于多时间尺度需求侧响应模型的网损优化方法对网损优化提供了一种新思路，为电价的制定提供了一个参考。

所提方法以网损的降低为目标，不同时段的网损分别乘上各自时段的电价，可以得到损失的电费。网损是通过MATpower进行潮流计算获得。在算例中将IEEE30中的一部分节点用需求侧响应求出的用电量来代替，再通过MATpower进行潮流计算得到峰、平、谷3个时段各负荷支路的有功损耗，最终累加得到各个时段的网损。