黑洞的理论预言和观测证认

侯嘉昊，袁业飞

(中国科学技术大学 物理学院 天文学系，安徽 合肥 230026)

2020年诺贝尔物理学奖一半授予罗杰·彭罗斯(Roger Penrose)，另一半授予赖因哈德·根策尔(Reinhard Genzel)和安德烈娅·盖兹(Andrea Ghez)，以表彰他们“发现了宇宙中最奇特的现象之一——黑洞”. 前者在理论上证明了广义相对论框架下黑洞的存在性，即引力塌缩将导致黑洞的奇点不可避免；后者则通过观测银河系中心恒星的轨道运动证实了银河系中心存在一个大约400万太阳质量的暗天体，且该暗天体的质量应该在最近恒星的近心点(125天文单位，约1.9×1010km)之内,超大质量黑洞是目前唯一合理的解释. 本文从黑洞概念的发展历史出发，对今年诺奖得主的主要工作进行概要性介绍.

1 黑洞理论

1.1 早期历史

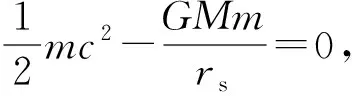
牛顿力学是建立在绝对时空观基础之上的. 绝对时空观认为时间和空间是绝对的，时空可以影响物质的运动，因为万物都存在于时空之中，但物质绝对不可能影响时空的性质. 爱因斯坦的相对论革新了人们对时空的认识. 狭义相对论统一了时间和空间，但时空仍然是绝对的. 广义相对论放弃了绝对时空的概念，认为物质和时空存在相互作用. 物质可以改变时空的性质，使得时空弯曲，而弯曲时空决定时空中物体的运动. 在广义相对论中，不存在引力这种相互作用. 地球绕着太阳公转，本质上是由被太阳弄弯曲的时空性质决定的. 时空弯曲由时空度规(gμν)刻画，爱因斯坦于1915年11月18日发表了正确地决定时空如何弯曲，即决定度规的引力场方程，这代表着广义相对论的正式建立. 广义相对论场方程发表后不到2个月，德国天文学家卡尔·施瓦西(Karl Schwarzschild)便得到了真空场方程的静态球对称解[1]，采用施瓦西坐标系dxμ={dx0,dx1,dx2,dx3}={t,r,θ,φ}，时空间隔可表示为

r2(dθ2+sin2θdφ2)≡gμ νdxμdxν,

(1)

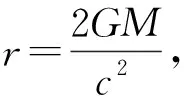
1.2 黑洞的存在性与奇点定理

自施瓦西黑洞提出以来，人们对于有关黑洞存在性的争论便未停止. 另一个需要回答的问题是，宇宙中黑洞能形成吗？恒星内部不断发生热核反应，提供了气体压、辐射压与引力抗衡，维持流体静力学平衡. 恒星内部氢燃烧结束之后，会发生超新星爆炸，外壳层膨胀，核区塌缩形成白矮星和中子星这样的致密星，根据后来的研究，甚至直接形成黑洞. 假设白矮星内部的压强由电子简并压提供，1930年，年仅19岁的苏布拉马尼扬·钱德拉塞卡(Subrahmanyan Chandrasekhar)发现白矮星存在最大质量，约为1.4倍太阳质量，后人称之为钱德拉塞卡极限[4]. 假设存在中子星，其内部压强由中子简并压提供，1939年奥本海默(J.R.Oppenheimer)和沃尔科夫(G. M. Volkoff)又进一步发现中子星也存在质量上限，约为0.7倍太阳质量，即奥本海默极限[5]. 一个很自然的问题是，当致密星质量达到最大值之后，电子或中子简并压不足以与引力抗衡时，它们会塌缩成黑洞吗？1939年，奥本海默和斯奈德(H. Snyder)通过求解球对称尘埃物质(内部压强为零)的场方程发现在引力的作用下尘埃会不断收缩最终塌缩为奇点[6]. 他们研究的对象为质量大于0.7倍太阳质量的中子星，因其超过奥本海默极限，中子星内部压强无法与引力抗衡，导致星体在引力的主导下塌缩. 为了简单起见，假设在引力塌缩过程中星体内部压强近似为零，并且忽略由于旋转等因素引起的球对称偏离，最终计算表明在随动观测者看来具有典型恒星质量的中子星塌缩为黑洞的时标仅为毫秒量级！这似乎是关于黑洞存在性的第一个理论上严格的证明，但许多人对此提出质疑，原因是球对称的条件过于苛刻，现实中并不存在. 当星体具有角动量时很难想象所有物质最终会塌缩到一点. 1963年，利夫希兹(E.M. Lifshitz)和哈拉特尼科夫(I.M. Khalatnikov)指出[7]，时空奇点的存在并不是相对论宇宙模型的直接推论，并且考虑一般情形下任意的物质分布不能直接证明奇点的存在. 惠勒(J. A. Wheeler)也表明了他的担忧：塌缩的星体会不断将自身物质转换为引力辐射而最终蒸发殆尽. 有关黑洞存在性的理论研究陷入了停滞状态.

类星体的发现重新点燃了人们研究黑洞的热情. 正是受到类星体发现的鼓舞，1963年彭罗斯(R.Penrose)开始深入研究黑洞是否存在奇点，最终做出了革命性的工作. 尽管当时克尔已经得到了旋转解，但其仍具有很高的对称性，故仍不能代表一般情形. 彭罗斯放弃了球对称物质的假设，仅对其能量密度提出正定的要求，为此他引入拓扑学来研究相关问题并创造性地提出“俘获面”(trapped surface)概念. 在1965年发表的文章中[8]，彭罗斯以时空上一类空超曲面(柯西面)作为物质的初始分布，假设一开始物质按照球对称分布形式进行引力塌缩，故而外部的真空部分可用施瓦西度规描述. 此时无限远处观测者只可接收到施瓦西半径之外的信号. 当物质收缩到施瓦西半径以内时，周围的时空便出现类空球面，即俘获面. 俘获面是闭合的类空二维曲面，任意2条与其正交的类光测地线会在未来某点相交(见图1). 俘获面一旦形成，即使物质的分布发生变化如偏离球对称等，也会一直存在. 而在正定的能量密度条件下，俘获面内部的所有物质随着时间推移最终都会汇集到径向坐标的原点，故时空的奇点是不可避免的. 文献[8]中的内容被称为彭罗斯奇异定理1965，该定理表明若物质的初始分布非常不平坦具有俘获面，且物质场满足合理的条件，则爱因斯坦场方程意味着时空必然具有奇异性.

图1 彭罗斯引入的俘获面示意图(F4是俘获面T2的编时未来集，B3是F4的边界. 图中为球对称情形，对偏离球对称同样适用)[8]

彭罗斯的讨论详细如下. 先讨论正能量条件. 所谓的正能量条件是说，在时空中任一点所有的类时测地线tμ满足：

(2)

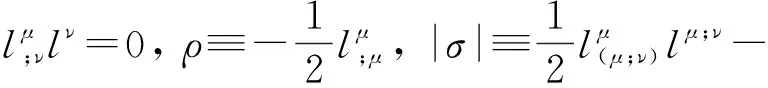
(3)

图2直观地解释了俘获面的概念[9]. 其中三维类空的空间已被压缩为二维平面，即用二维平面代表三维空间. 平面向上的法线方向代表时间演化方向. 星体的表面用黄色的圆圈表示，从星体表面发出的、沿着径向向外传播的光用蓝色的圆圈表示，向内传播的光(假设光可以自由地向内传播，类似中微子)用红色圆圈表示. 作为对比，图2(a)显示的是静态时空. 在静态时空中，星体的大小基本不随时间演化，从星体表面发出的向外传播的光的直径越来越大. 图2(b)显示的是引力塌缩的时空，且在该时空中，随着时间的演化，星体的半径越来越小，从星体表面发出向外和向内传播的光的半径也在不断减小，甚至小于上一时刻星体的半径. 在这种情况下，星体的表面就被彭罗斯称之为未来俘获面. 在引力塌缩过程中，一旦出现俘获面，随着时间的演化，俘获面最终会塌缩到一点——奇点.

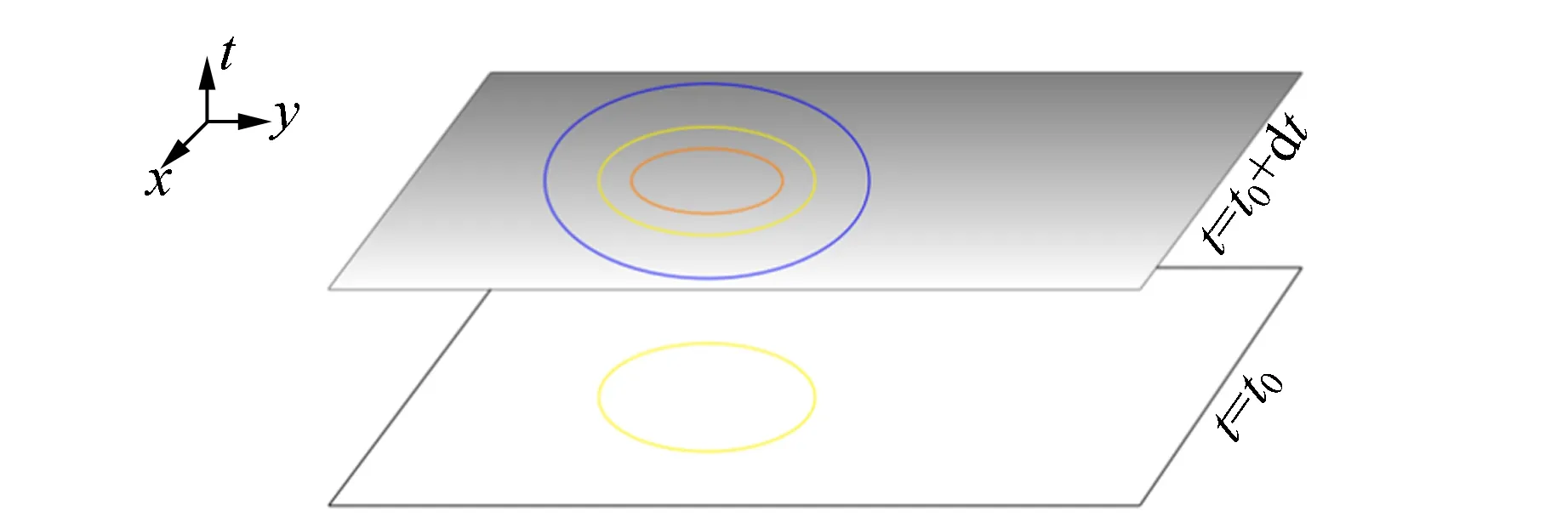
(a)静态时空

在这一时期彭罗斯的其他主要工作包括：

1963年提出利用共形等度规映射

(4)

将时空共形嵌入至更大的时空，从而把原时空中的各类无限远(未来类时、类光无限远等)拉近，以研究弯曲时空的渐进行为[10]，利用此方法绘制的时空示意图称为彭罗斯图(图3)，在彭罗斯图中类光测地线为45°和135°的直线.

图3 时空的彭罗斯图(时空的无限远点经过共形变换后被拉近)[10]

1969年提出从转动黑洞提取能量的方法，即彭罗斯过程[11](图4). 其原理是利用克尔黑洞在视界与无限红移面(与静止极限面重合)之间的能层中物体在远处观测者看来可能具有负能态的特性，负能态粒子的出现需要同时满足与黑洞反转以及其运动速度接近光速这2个条件. 若令一进入能层的物体分裂为具有正能和负能的2部分，则具有正能部分逃逸黑洞后的总能量会增加，负能部分被黑洞吸收并减少其总角动量，从而实现从转动黑洞中提取黑洞的内能(转动能).

图4 彭罗斯过程示意图(图中圆圈为其附近圆点处发出的光经过一定时间后所能到达的区域)[11]

1970与霍金[12]一同提出新的奇异定理，证明在宇宙大爆炸模型中过去奇点的存在，也就是沿着时间的反方向，宇宙大爆炸类似引力塌缩，也存在奇点.

彭罗斯的一系列工作标志着天体物理学进入了新的纪元，而黑洞也作为描述这一奇特的引力异常现象的名称固定下来.

2 黑洞观测

2.1 类星体的发现

人们对于与黑洞有关的实际观测最早来源于上世纪60年代类星体3C 273的发现[13]. 1908年爱德华·法斯(Edward Fath)观测到NGC 1068的核区有强的发射线. 1918年赫伯·柯蒂斯(Herb Curtis)发现“一条奇怪的直线”连接至M87的核心. 1939年格罗特·雷伯(Grote Reber)发现射电源天鹅座A. 由于这些源的反常现象(全波段辐射、具有发射线等),最初人们并不清楚它的本质，事后我们知道NGC 1068的核区的发射线来自核区超大质量黑洞吸积盘辐射照射盘上或周围冷气体产生的荧光发射线；连接M87核心的“直线”是来自核区超大质量黑洞的星系尺度的喷流；而天鹅座A的射电辐射应该来自黑洞喷流中相对论性电子的同步辐射. 1963年荷兰天文学家马尔滕·施密特(Maarten Schmidt)第一个意识到射电源3C 273的光谱中无法证认的宽发射线，其实是高红移后的氢的巴尔末线和电离氧的谱线，其红移值为0.158[13]. 根据宇宙大爆炸理论，宇宙学红移0.158的天体距离地球约为24.8亿光年(760 Mpc)，施密特从而成为“类星体”的发现者. 根据类星体的距离，类星体的典型光度高达1039J/s，该光度大概是整个银河系总和的1 000倍. 后续研究表明这些类星体其实是位于其他星系中心的致密、高光度的辐射源，也被称为“活动星系核”，通常光度在典型星系的光度总和的2个量级以上. 一些科学家试图将类星体解释为超大质量恒星，但恒星质量过大会导致不稳定性与极短的寿命. 类星体的能源成了谜. 1964年埃德温·欧内斯特·萨尔皮特 (Edwin Ernest Salpter)、亚科夫·鲍里索维奇·泽尔道维奇(Yakov Borisovich Zeldovich)和伊戈尔·德米特里耶维奇·诺维科夫 (Igor Dmitriyevich Novikov)猜测类星体的能源来自质量高达109倍左右太阳质量的黑洞吸积周围气体释放的引力能. 在彭罗斯提出了有关黑洞的一系列理论后，超大质量黑洞成为解释类星体的主流模型. 1967年约翰·阿奇博尔德·惠勒(John Archibald Wheeler)和雷莫·鲁菲尼(Remo Ruffini)正式使用“黑洞”一词[14]，并使用至今.

2.2 银河系中心存在黑洞

自黑洞模型被用于解释类星体以后，1969年唐纳德·林登贝尔 (Donald Lynden-Bell)[15]提出多数星系中心都存在黑洞. 他认为星系中心的黑洞是类星体的遗留物，通过估计死亡类星体的数量与主要星系的数量可比拟从而推断出星系中心存在黑洞. 2年后，他与马丁·里斯 (Martin Rees)[16]一起讨论了银河系中心超大质量黑洞的存在性，并且提出了几类关键的观测方法，包括探测银河系中心0.2 pc内的水的复合线来确定其速度，从而判断该区域是否存在一个质量为107～108M⊙的物体；利用超长基线干涉仪(VLBI)测量弱信号从而确定银河中心黑洞的尺寸；探测银河系中心远红外波段的流量等. 在20世纪90年代早期，望远镜的角分辨率不足以在空间上区分彼此相距只有银河中心黑洞的施瓦西半径量级的物体，故只能通过观测附近的恒星与气体的轨道来确定银河系中心物体产生的引力势能，得到其质量密度并与各类已知天体的密度对比确定其具体组成. 1995年三好诚(Makoto Miyoshi)[17]等人观测距离为7.3 Mpc的星系NGC 4258核心处的水脉泽. 利用VLBI他们以高于毫角秒的角分辨率绘制了水脉泽的位置与速度分布图，得到旋转曲线后根据开普勒定律确定了中心物质密度在109M⊙pc-3量级，远大于银河系中已知密度最大的稳定多体系统球状星团，后者的密度在105M⊙pc-3量级. 观测结果排除了星系核心附近气体的运动是源于中心的致密星团的假设，进一步肯定了黑洞的存在. 银河系中央几个pc内存在大量的星团与炙热气体，是用于确定银河系中心致密射电源人马座A*产生的引力势能的绝佳观测对象. 若银河中心确实存在超大质量黑洞则周围星体的速度v应与其距离中心半径r的1/2次方成反比，正如太阳周围的行星一样；而对于空间上较为分散的致密星团，则根据星团的具体密度周围星体的速度可能随半径一同上升或者与半径的依赖关系变低. 因此对于银河中心附近星体速度的观测成为确定黑洞存在的关键.

2.3 盖兹和根策尔的工作

由于斑点成像技术的极短曝光时间使得只有最亮的星体能够成像. 为了长期追踪单个恒星的轨道，盖兹与根策尔团队使用了最早于1953年由霍勒斯·W·巴布科克(Horace W.Babcock) 提出的自适应光学技术[19]. 该技术的目的为修复大气湍流对光波波前的扭曲，通过在观测对象附近安置人造已知光源得到波前的扭曲情况，随后通过望远镜焦面后的小型可变形镜面对波前实时矫正，最后由反馈回路实现对观测物体光波波前的矫正. 此技术可延长曝光时间并实现了利用光谱仪研究星体，从而得到星体的组成信息与径向速度. 运用新技术后，2个团队开始了单一星体轨道的追踪观测. 研究的星体被标记为S2，它绕人马座A*运动轨道周期很短，只有大约16年[20]，并且轨道呈现高度的椭圆形状(图7)，偏心率e=0.88，与人马座A*的最近距离只有17光时，相当于质量为4×106M⊙黑洞施瓦西半径的1 400倍. 2个团队测得的数据彼此符合得很好，对数据进行分析后他们发现S2轨道内其余发光星体、暗物质等物体的影响在估计中央物体质量时可忽略[21]，从而得到中心质量大约为4×106M⊙，考虑轨道大小后这意味着中心物体的密度至少为5×1015M⊙pc-3. 这些观测结果最合理解释是银河系中心的致密物体为超大质量黑洞. 2个团队分别在ESO与Keck天文台对S2轨道进行了长达26年(1992-2018)的观测(图8)，结果为银河中心存在超大质量黑洞的假设提供了运动学层面的有力证明. 此外2个团队还利用2018年S2恒星经过近心点的机会，探测到了相对论效应下的轨道进动，这是符合理论计算的一个了不起的实验成果.

图5 人马座A*周围星体的速度矢量图[18][图中距离是相对于初始位置(1994.4.27时恒星的位置)，R.A.为赤经，Dec.为赤纬]

图6 星体投影速度与人马座A*中心投影距离的函数关系(由曲线可推断出银河中心的黑洞质量大约为2.5×106M⊙，考虑后续观测数据后这一估计增加至4×106M⊙)[18]

目前的观测数据还不能对在黑洞几百个施瓦西半径内的物体进行细致研究，但红外耀斑的偶然发现为进一步研究提供了可能[22]. 利用具有更高角分辨率的GRAVITY可由这些耀斑追踪人马座A*的最内部区域[23]. 观测发现这些耀斑起源于黑洞的紧邻区域，以光速的30%围绕中体物体做轨道运动，距离中心只有3～5个施瓦西半径，刚好位于质量为4×106M⊙的Kerr黑洞的最小稳定圆轨道外. 这些结果也为银河系中心致密物体为超大质量黑洞的假设提供了额外的证明.

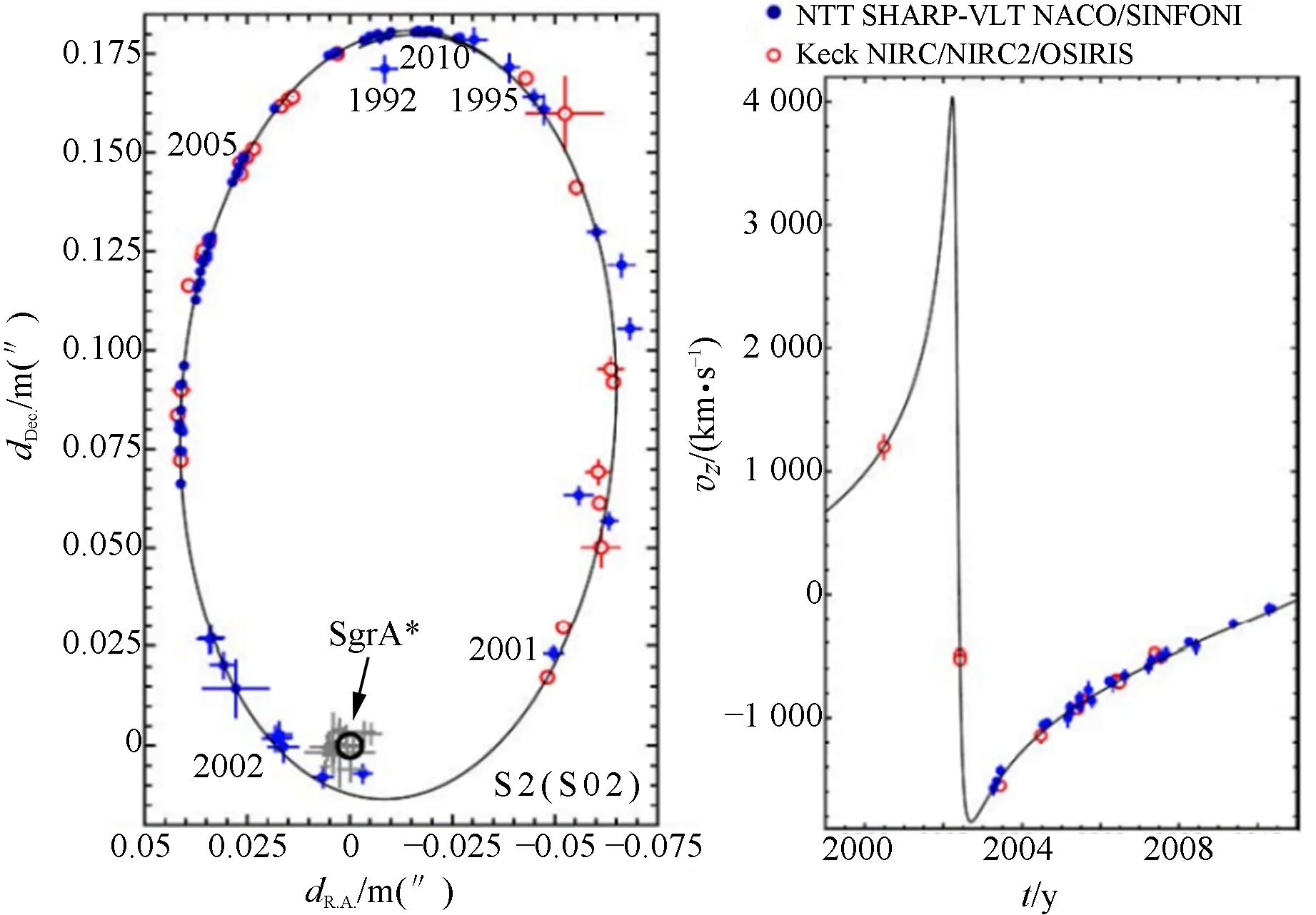
(a)投影轨道 (b)径向速度图7 S2的投影轨道与其径向速度[24](蓝色与红色圆点分别代表由NTT与Keck望远镜得到的数据，灰色十字为人马座A*的红外波段辐射源. 图中显示的是与人马座A*射电源的相对位置)

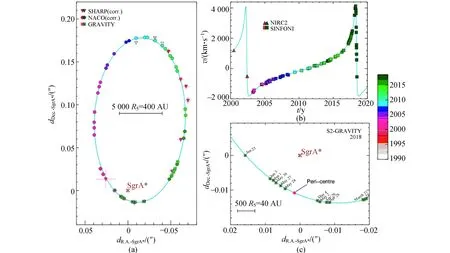
图8 在26年间(1992-2018)对S2观测结果的总结[23][图(a)轨道显示了与人马座A*射电源(图中褐色十字处)的相对位置. 图(b)为S2径向速度与时间函数关系图，图(c)为2018年测得的轨道近心点附近的放大图，S2分别于2002年4月与2018年5月运动至近心点. 各图中青色曲线为考虑相对论效应后与实测数据匹配度最高的拟合曲线]

3 结束语

自彭罗斯提出有关黑洞的一系列理论以来，人们对黑洞有了全新的、整体的认知. 随着之后技术的发展与观测水平的提高，人们又逐渐在实际观测中得到黑洞存在的证据. 爱因斯坦曾经说过：“宇宙最不可理解之处是它是可理解的.”黑洞，这一宇宙中最奇特的物体，正慢慢被我们揭开它神秘的面纱.