渗透水化对饱和页岩吸水的影响

冷静怡，王琳琳

中国石油大学(北京) 安全与海洋工程学院，北京 102249

*通信作者, linlin.wang@cup.edu.cn

0 引言

21世纪初期以来，美国页岩气革命取得了巨大的成功。其页岩气产量从2000年的约100×108m3/a迅速增长至2015年的近4000×108m3/a，约占美国天然气年产总量的50%。页岩气技术的革命极大程度地加速了美国由一个石油进口大国走向能源独立的进程[1]。此外，预计到2040年，美国原油生产与消费量的缺口将仅有7%，可见页岩油气资源在石油行业寒冬期为美国提供了极为有利的能源保障[2-3]。

我国作为全球现有的4个实现了商业开采天然气的国家之一[4]，在“十二五”期间通过在四川盆地地区对下古生界的海相页岩进行不断地探索和研究，在页岩地层中进行钻采施工的技术水平得到了显著的提高。这些现场试验所获得的经验使得我国页岩气开采开发进程走向了一个新的历史阶段。截至“十二五”末，我国海相页岩气探明的地质储量已经达到5441×108m3，2015年海相页岩气的总产量达到45×108m3[5]，页岩油气凭借其相当储量高、低污染等优势，在我国目前资源紧缺、能源结构急需转型的能源背景下，正逐步发展成为我国石油天然气行业所关注的重要课题[6-8]。可以说，无论是从我国当前不合理的能源消费结构来看，还是从全球石油工业发展趋势来看，页岩油气资源的开发将在很长一段时间内成为我国油气行业工作者研究的重点问题。

由于页岩储层的渗透率非常低，为了获得具有商业价值的油气流，需要通过水力压裂的方式提高近井地带的渗透率。由于页岩地层具有脆性，天然裂缝较为发育，在水力压裂过程中，通过将大量的压裂液注入到地层中，达到地层的破裂压力，以使得地层中原有的微裂缝进一步开裂，在近井地带建立复杂缝网，从而大幅地提高页岩气井近井地带的渗透率，最终达到增产的目的。为了尽可能降低注入液对原始地层的污染，在压裂施工结束后需要对压裂液进行返排，然而大量的现场统计资料显示，压裂液的返排率通常很低[9-10]。这些滞留在地下的压裂液会与页岩储层发生物理化学反应，对页岩油气生产和地下水等环境造成一定影响。部分学者认为，未返排出的压裂液可能会进入到地下水层中。但也有人认为页岩储层本身具有一定的储水能力，这些水会被束缚在页岩储层中而不是进入到地下水中[11]。此外，很多油田现场的数据表明，压裂后焖井一段时间，页岩储层由于压裂液中水的作用会产生微裂缝[12-13]，这些微裂缝会使得页岩渗透率增大，从而大幅提高页岩气井在生产初期的产气量[14]。但也有人认为压裂液与页岩之间的反应虽然会在生产初期有增产的效果，但吸水会使得页岩发生膨胀使一些原有的裂缝闭合[15]，故从长远角度看，未返排出的压裂液会降低页岩气的产量。最后，在为核废料寻找合适储层时，也存在地下水污染问题[16]。为了解决这些问题，本文对饱和页岩中的吸水机理进行研究。

1 饱和页岩吸水的理论模型

1.1 饱和页岩吸水的微观机理

页岩吸水的微观机理较为复杂，在饱和页岩中主要包含两种机理：渗透水化和表面水化。这两种独特吸水方式是由页岩中的黏土矿物造成的。要理解黏土矿物的吸水的微观机理，首先要理解黏土矿物的微观结构。黏土矿物的微观结构可以分成三级[17]。第一级是黏土矿物的片状结构，主要包含两种：硅氧四面体片(T)和铝氧八面体片(O)。在硅氧四面体中，硅原子位于四面体的中间，氧原子位于正四面体的四个顶点；铝氧八面体中，铝原子位于正八面体的中心，八个羟基分别位于正八面体的八个顶点处。但是在自然界中，这些硅原子和铝原子常常会被一些较低价态的阳离子所代替，如铁离子、镁离子等[18]。硅氧四面体片和铝氧八面体片按照1:1或2:1的比例相互结合可以形成具有TO或TOT型层状结构的两大类黏土矿物。两个相邻的层之间的距离成为层间域。随着环境湿度、所处溶液的活度的改变，水分子可能进入到层间域中使得层间域的大小发生变化，即相对湿度(或活度)的改变会引起页岩孔隙度、含水量的变化。这种通过改变相对湿度(或活度)从而改变页岩含水量的过程称为表面水化。

图1 渗透水化、表面水化微观机理示意图Fig. 1 The micro mechanism of osmotic effect and surface hydration

黏土的层状结构之间通过静电力、分子间作用力等相互结合即可形成不同的黏土颗粒结构[19]。由于黏土矿物中的阳离子经常会被其他较低价态的阳离子所代替，所以黏土矿物颗粒的表面通常是带有负电的。为了平衡这些多余的负电荷，维持电中性，在黏土颗粒表面会吸引许多可交换阳离子，形成扩散双电层。如图1(a)所示，扩散双电层分为两个部分，一层称为Stern层，该层中只有一层阳离子被吸附在黏土表面；而另一层为扩散层，该层中的阳离子与负电表面的联系不是很紧密，可与溶液中的阳离子发生交换，这些离子称为可交换阳离子。当页岩颗粒之间距离较近时，两个黏土颗粒表面的扩散双电层相互靠近发生重叠，由于静电排斥作用，两个扩散双电层间不允许阴离子通过。同时为了维持电中性，阳离子也无法通过这个区域，只有不带电的粒子才可以通过。这种性质类似于半透膜的选择透过性，即半透膜两侧的浓度差所产生的渗透压差会使水由低浓度一侧流向高浓度一侧。由这种性质导致的吸水过程称为渗透水化，如图1(b)所示。综上所述，可见页岩层间域的可变性赋予了页岩较强的储水能力，而这种类半透膜性质赋予页岩较强的吸水能力[20]。

由于目前对表面水化机理的研究较少，在建模过程中本研究不考虑表面水化对渗流过程的影响，只考虑页岩储层中水压和渗透水化对页岩吸水过程的影响，建立饱和页岩吸水过程在笛卡尔坐标系下的一维模型。研究初始状态下饱和一定浓度的盐溶液，一端为恒压、定浓度边界，另一端为封闭边界的一维线段中的页岩吸水变化规律，考虑压力差和渗透水化引起的吸水。由于考虑了渗透水化的影响，页岩的吸水量会受到孔隙中水溶液中的离子浓度的影响，原有的用于描述渗流过程的达西公式将不再适用，需要对其进行修正。

1.2 饱和页岩吸水的控制方程及求解

为了考虑渗透水化，即页岩的类半透膜性对页岩吸水过程的影响，页岩的吸水过程的运动方程可以通过对达西公式进行修正得到[21]：

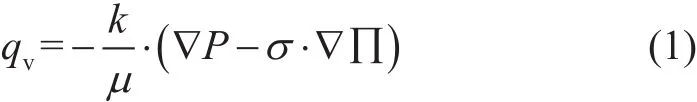
这里qv是水的流动速率(m/s)；k是饱和水时的水相渗透率(m2)；μ是水的黏度(Pa·s)；P是水压(Pa)；σ是有效渗透系数，用于描述渗透水化的强弱，用ks/k表示(考虑渗透水化时的渗透率ks和不考虑渗透水化时的水相渗透率k之比)；T是地层温度(K)；C是注入液的离子浓度(mol/m3)；Π是渗透压(Pa)，其表达式如下[14]：

其中ν是盐中所含的离子数(-)；R是理想气体常数(J/(mol·K))。此外，式(1)中的修正项与达西项符号相反是由于渗透水化使得水由低浓度向高浓度流动。为了描述修正项中出现的浓度的变化，给出溶质的运动方程如下：

其中，qs是指溶质的摩尔流动速率(mol/(m2/s))；De*是指有效扩散系数(m2/s)；根据Katchalsky，Curran，Bader 和Kooi的文章[22-23]，对于一个不完美的半透膜而言，De*和σ之间的关系如下：

此外，公式(3)中等式右侧的第二项表示由于水的流动引起的溶质离子的迁移(即对流作用)。根据Peclet数[24]，由于页岩的渗透率很小，对流作用对溶质的流动影响可以忽略不计，故方程(3)可以简化为[21-22]

水的质量守恒方程可以表示为[23]：

其中ρ表示注入水的密度(kg/m3)。

溶质的质量守恒方程为[23]

其中，w是指溶质的质量分数；Ms是溶质的摩尔质量(kg/mol)。

为了求得解析解，本研究中做出一系列假设以简化方程。这些假设包括：认为有效渗透系数，饱和页岩中水相渗透率，水、地层岩石的压缩系数为常数，即在整个吸水过程中，这些参数不发生变化；认为地层为均质、各向同性地层。基于这些假设，由公式(1)和公式(6)可以推出一维的压力传递公式如下：

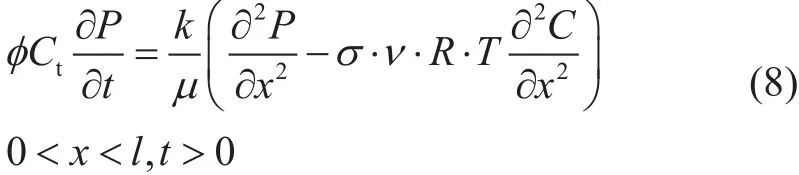
其中Ct为综合压缩系数，是注入液和岩石的可压缩系数之和(Pa-1)；l是一维页岩吸水模型的长度(m)。此外，由公式(5)和公式(7)可以推出溶质扩散的控制方程如下：

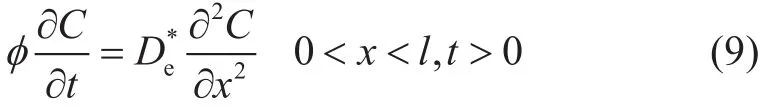
运用拉普拉斯变换，傅里叶级数展开等数学物理方程中涉及到的方法，可以解出在给定的边界条件和初始条件下，浓度分布随时间的变化如下：

压力分布随时间的变化关系：

至此，我们已经得到了饱和页岩吸水过程中压力与浓度分布随时间的变化关系。

2 结果与分析

在上节中我们已经得到了饱和页岩吸水的数学描述。本节中，为了对所求得的解析解有更为直观的认识，我们在上一节所求出的解析解中代入各参数在页岩地层中的常见取值，画出浓度和压力分布变化图，并对其进行分析，探究不同吸水机理对总吸水量的影响。分析中所用到的各参数的取值如表1所示。

表1 分析所用参数图Table 1 Values of parameters used in analysis

根据所给数据和第一节所求得的解析解，可以画出在σ= 0.01时浓度和压力分布随时间的变化及两种机理产生的吸水量的变化图分别如图2、图3、图4所示。注意由于建立的模型为一维模型，故计算出的吸水量的单位为米。此外，吸水量为负时表示排水。下面对所得的曲线进行分析。对比浓度和压力分布变化图可以发现：与压力相比，浓度的衰减较为缓慢，需要约100 h才能衰减到初始浓度的5%以下。在吸水过程的初期，渗透压作用对总吸水量的贡献很小，但在吸水的后期，吸水量主要是由渗透水化引起的。

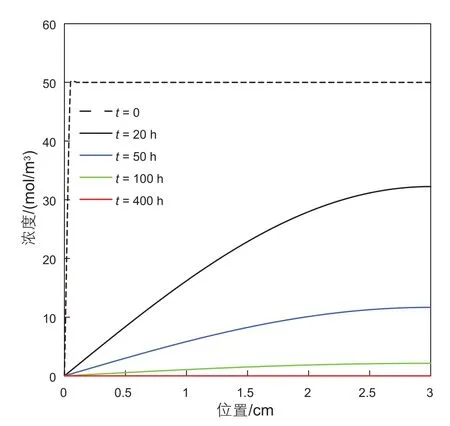
图2 浓度分布随时间变化图Fig. 2 Concentration distribution at different time

如图3(a)所示，与浓度相比，压力的衰减很快，只需要约15 min即可衰减到初始压力的5%。但如果改变纵轴的单位，观察较长时间后压力分布的变化，可以发现水压并没有迅速趋近于零，而是缓慢地衰减(如图3 (b)所示）。为了更直观地分析渗透水化的存在对压力的影响，我们取σ= 0，计算只有常规达西流动的情况下的压力变化情况。根据计算结果可以发现，在吸水初期压力变化情况与σ= 0.01时很接近，但是在吸水后期，达西流动的水压几乎为零。由此可以说明，后期压力的变化是由于渗透水化的存在而造成的，即压力变化与浓度变化之间存在一定的耦合关系。同时也可以说明，前期的吸水量主要是由水压变化引起的，而后期的吸水量中虽然压力也有一定的贡献，但其实压力的变化也是由于渗透水化的存在才产生的。故后期吸水的主控因素仍为渗透水化。

图4是吸水量随时间的变化关系，可以非常明显的看出水压主导吸水量的时间很短，但其引起的吸水量与渗透水化导致的吸水量相比很大。虽然渗透水化主导的吸水量相比之下较小，但是持续的时间较长。这与前文中对浓度和压力分布变化的分析结果相符合。渗透水化作用主导的吸水持续时间较长，是因为通常情况下浓度的扩散速度低于压力的传导速度，本质上是浓度方程的扩散系数通常远小于压力方程的扩散系数。此外，应当注意的是渗透水化对吸水量的贡献有两种：由于浓度差导致的吸水以及由于其对压力的影响而导致的吸水量变化。这两种作用导致的吸水量变化方向相反，故渗透水化对总吸水量的影响并不明显。根据计算结果，在浓度场分布达到平衡时，两种作用方式引起的吸水量相互抵消，即渗透水化在系统达到平衡时对总吸水量无影响。

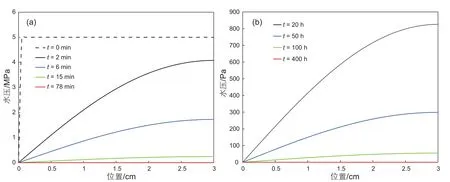
图3 水压分布随时间的变化图(图(a)表示较短时间段内水压分布的变化图，图(b)表示在较长时间内水压的变化情况)Fig. 3 Hydraulic pressure distribution at different time (Fig (a) indicates the hydraulic pressure distribution within early stage,Fig (b) indicates hydraulic distribution during the late period)

图4 吸水量随时间的变化关系图Fig. 4 Water uptake variation with time

3 结论

本文主要研究了考虑渗透水化的页岩 吸水过程。由于在考虑渗透水化的情况下，页岩的吸水过程还会受到浓度变化的影响，故本文对传统的达西公式进行修正，建立了饱和页岩吸水的数学模型。同时，运用数学物理方程中的相关方法，给出了一维情况下考虑渗透水化的页岩吸水过程的解析解。通过分析得到的解析解可以发现：(1)渗透水化的存在不仅使浓度的变化对吸水量产生了贡献，同时也会对水压的传递产生影响，即常规的达西渗流与渗透水化之间存在耦合关系。(2)在页岩储层的常见取值条件下，压力分布达到平衡所需时间较短，浓度分布达到平衡用时较长。(3)水压差只在页岩吸水的初期较短时间内起到较为明显的作用；而渗透水化在初期对吸水量的贡献很小，但在后期可以持续作用较长的时间，通过浓度差及其对压力的影响两种方式影响吸水过程。由于两种作用方向相反、数值接近、并在平衡时相互抵消，故渗透水化对总吸水量影响不大，即渗透水化的存在会显著地延长吸水平衡时间而对平衡时页岩的吸水量无影响。