基于差异共振声谱仪多阶共振模式的弹性模量频散测量

唐跟阳 ，董春晖 ，王尚旭 *，曾心，任保德

1 中国石油大学(北京)地球物理学院，北京 102249

2 教育部复杂油气藏勘探开发工程研究中心，北京 102249

*通信作者, wangsx@cup.edu.cn

0 引言

实验室低频测量提供了岩石在声波和地震频段的物理性质的直接信息，在地震井间、地震解释和储层特征描述方面具有重要应用价值。目前有几种实验室测量技术可用于测量岩石样品在低频和低振幅下的弹性和黏弹性性质，如共振棒法[1-2]和应力—应变法[3-5]。共振棒法可以测量岩石样品的纵波波速和横波波速及其衰减因子[6]。测量的频带位于声波频率范围(～1～20 KHz)，具体频率取决于样品长度。扭转摆技术和受迫振动法可以在更低的频带内使用，扭转摆技术测量频带为25～400 Hz[6]，受迫振动法测量频带为5～2000 Hz[5]，包含地震频带。最近一种称为差异共振声谱(DARS)的替代性低频测量仪器在无孔和多孔材料的测量上被证明是一种在～1 KHz频率下测量样品体积模量的有效技术[7-9]。Zhao等利用该技术在600 Hz和1 MHz的条件下测量人工砂岩和储层砂岩的体积模量的频率依赖性[10]。因此，DARS测量方法成为低频测量的有效技术之一。结合这些技术，岩石弹性性质的直接低频测量通常用于研究不同类型岩石样品的物理特性[2,4-6,9-22]。

应力—应变法必须避免整个测量系统的共振，包括振动器、支撑装置和容器的共振，而共振棒技术和DARS方法则使用系统的共振模式来估计样品的声学特性。这些技术有它们自己的优点和局限性。应力—应变法可以扩展至一个相当宽的连续频率范围(1～2000 Hz)，提供更多的测量频率；然而，该测量方法存在试样制备困难、应变信号微弱等问题。共振棒技术可以提供几个共振频率下的测量结果，构成地震和超声波频段之间的中频范围[23-25]；但是，该技术需要较长、耐用、均质的样品进行测量，因此将岩石样品限制在一定的类型和强度范围内。此外，使用该技术时，储层围压、孔压和温度控制较为困难。DARS方法可以获得岩石样品在第一阶共振频率(～600 Hz)时的体积模量，试样制备过程较为简单。但DARS测量方法往往仅使用第一阶共振频率来估计声学特性[9]，而忽略了使用更高阶共振频率以获取更多信息。

本文利用DARS系统的一阶和高阶共振，即第二和第三阶共振频率，来估计人工砂岩的体积模量。该测量技术提供了更高频率的测量，将频率范围从地震频段扩展到声波频段。本文改进了测量方法，利用3个参考样本来估计系统的校准参数。采用一种新的线性最小二乘反演算法计算标定参数和样品体积模量、密度。通过对共振腔内不同位置的校准参数的分析，可以得到最佳的测量位置，从而减少了精确反演所需的测量位置数量，提高了测量效率。

通过数值模拟和实际实验验证了该方法的有效性，并给出了测量值的误差估计。然后，将该技术应用于7个不同孔隙度的人工砂岩，测量它们在不同频率下的体积模量。体积模量随孔隙度/渗透率以及频率而变化，这可能是由波动引起的流体流动引起的。此外，由于样品表面开放且浸泡在硅油中，可以直接观察到流体交换效应。尽管波致流被认为是岩石中速度频散和衰减的主要原因[26-29]，然而对于频散的物理机制仍在进一步讨论和验证之中[5]，我们的测量结果有助于理解弹性模量频散的控制因素，有助于解决地震—测井频段之间的关联，进而提高地震解释的能力。

1 DARS测量与反演

DARS系统的原理如图1所示。该测量系统由一个中心为圆柱形铝腔的充液容器、容器底部的压电陶瓷震源、腔内的水听器、锁相放大器和由计算机控制的接收放大器所组成。震源和水听器(经过放大后)连接到由计算机控制的锁相放大器上。计算机还控制一个步进电机，在每次测量运行中，将测试样品沿空腔的轴线进行移动。容器内液体为二甲基硅油，黏度为5 cSt，密度为0.93 g/cm3，其声速(c)在25 ℃时为970 m/s。在空腔内特定位置引入测试样品后引起DARS系统共振频率变化，其扰动方程为[9]：

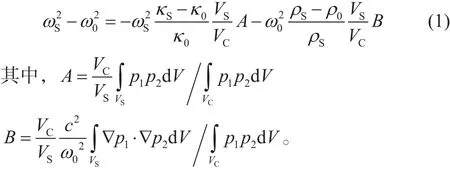
变量ωS和ω0分别是共振腔内有和没有样品的情况下整个系统的共振频率，并且p1和p2是在腔内的相应声压幅值。VS是样品体积，VC是空腔体积。A和B是DARS测量系统的校准参数。

对于充满硅油的理想共振圆柱体腔(两个开口端的p=0)，驻波的压力幅值沿其轴线具有谐波分布形式(图1)。在第一阶共振模式下，压力分布为沿轴线位置的余弦函数的形式。第一阶共振模式的共振频率由给出(L是腔的长度)。在第二和第三阶共振模式下，压力分布为类似形式的正弦或余弦函数，但共振频率加倍或呈3倍。在实际实验中，由于仪器几何形状和边界条件的影响，不同共振模式的共振频率与理想值会略有不同[9]。在共振腔中引入测试样品将进一步改变每种共振模式下的共振频率，并且该频率变化主要由公式(1)描述，其中系统校准参数和与相应共振模式的声压分布相关，反映无样品和有样品时共振腔内部压力场的物理特性。这组参数需要进行精确校准，较大的值会放大压缩率项，从而提高可压缩性的灵敏度和准确性。

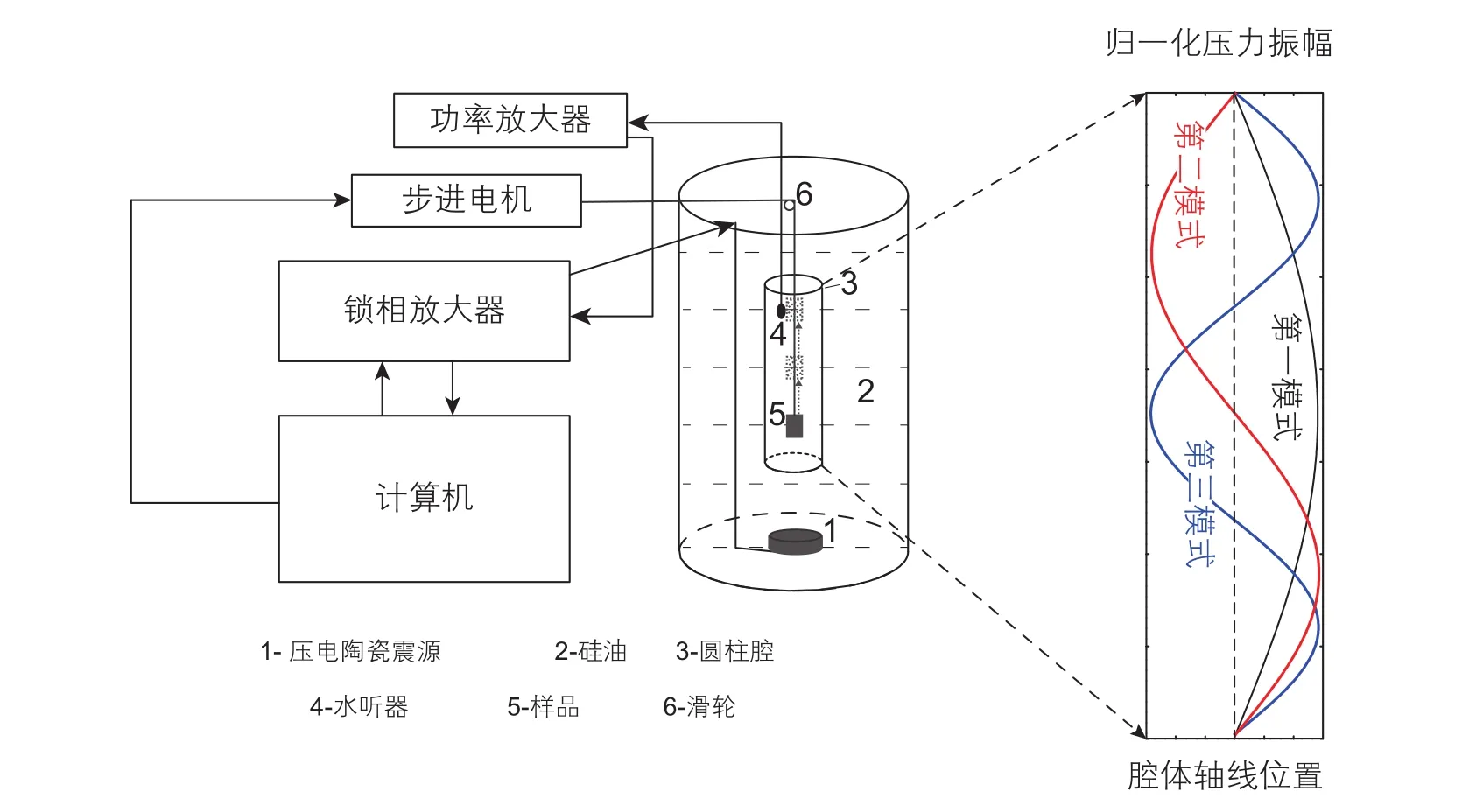
图1 理想条件下(没有加载样品)，第一、第二和第三阶共振模式下共振腔内的声压振幅分布Fig. 1 Under ideal conditions (no sample loaded), the sound pressure amplitude distribution in the resonant cavity in the first,second and third order resonance modes

该扰动方程已被用于估算一阶共振模式下岩石样品的压缩率(体积模量)和密度[10]。我们将证明扰动方程对高阶共振模式也是有效的。在本研究中，我们使用第一、第二和第三阶共振模式来估计样品的压缩率和密度。对于各阶共振模式，将样品放置在共振筒内部的不同位置进行测量，并按以下顺序进行测量：样品的可压缩性从高到低变化，例如空腔/参考样品＃1/参考样品＃2/测试样品/参考样品＃3/空腔。测量中使用了三个参考样品来校准参数A和B，以获得更高的精度。

在测量共振频率时，声学信号的频率扫描范围为系统的第一、第二和第三阶共振频率，分别为590 Hz至 610 Hz、1180 Hz至1220 Hz和1770 Hz至1820 Hz。目前，由于系统组成部分的相互作用造成了对其他共振的干扰，第四阶和更高阶共振模式没有被使用。对于每种共振模式，一旦获取了不同位置的参考样品或测试样品的所有共振频率，两组线性方程组中未知数A和B或未知数κS和1ρs使用方程(1)即可获得。对于参考样品，其压缩率和密度是已知的，因此，线性方程组的形式为

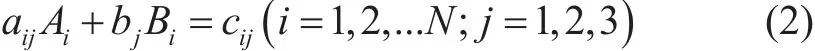
对于测试样本，获取系统校准参数后，可以得到一组以κS和1ρs为未知数的线性方程：

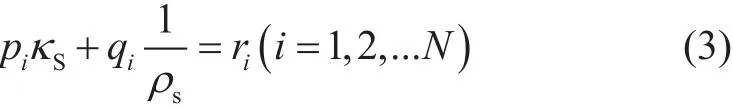
2 模拟与实验测试

为了验证扰动方程仍然可以表示DARS系统的第二阶和第三阶共振频率的变化，我们进行了数值模拟和实验来估计扰动方程的误差，并使用该方程估算一阶和高阶共振频率下的体积模量和密度。对于数值模拟，我们使用有限差分程序对真实的DARS设备建模，并获得不同共振模式下共振腔中的声压场[30]。该代码使用交错网格有限差分方法来近似求解圆柱坐标系下的波动方程。以一系列单频正弦波的叠加作为源函数来计算压力波场，以模拟实际实验过程。在共振腔一端记录的声压场的共振曲线可通过其振幅谱获得。一旦获取了空腔以及加载标准样品或假想样品(数值样品)时系统的共振频率，就可以通过上述反演方法获得假想样品的体积模量。对于数值模拟，我们设计了16个假想的固体样品，其信息列于表1。前9个样品具有相同的压缩率，但速度和密度不同。样品#2，#9和#14是参考样品，其物理性质与实际实验中使用的标准样性质相似。其余的假想样品具有不同的密度和速度，且覆盖了较大范围的体积模量。通过在模拟压力场的振幅谱上选取峰值振幅来获得与腔体内各个位置处的每个样品相对应的共振频率[30]。

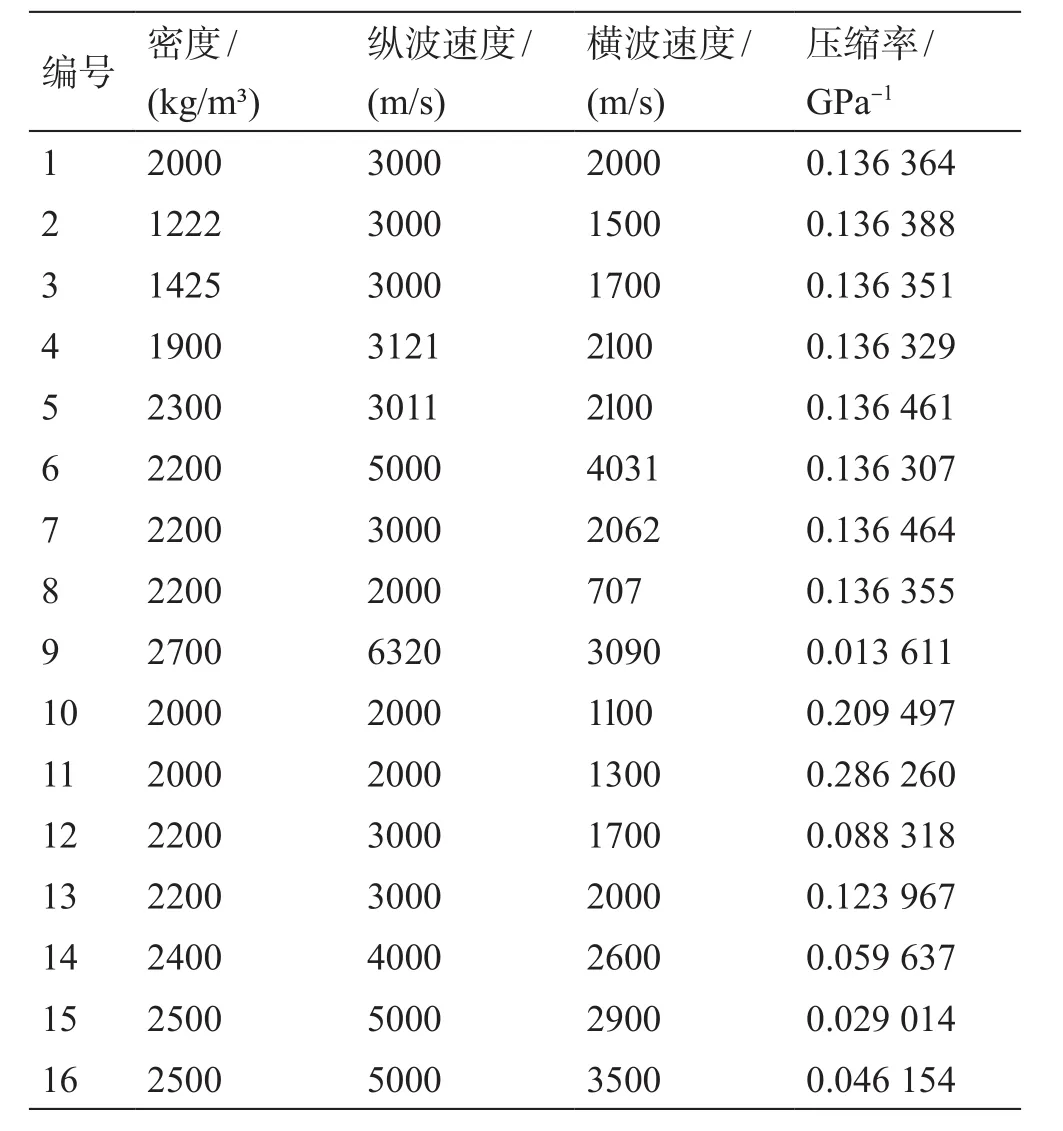
表1 假想样品的物理性质Table 1 Physical properties of hypothetical samples

采集共振频率的位置覆盖了共振腔的整个长度。对应于不同共振模式，样品#16的共振频率数据如图2所示，图中还显示了通过对样品#16数据的反演获得的参数A和B。需要注意的是，共振频率随测量位置的变化与压力波场随不同波长的变化有关(见图1)。在每个共振模式下，参数A与共振频率同相，而参数B与共振频率反相。这种变化趋势可以通过A和B的定义来解释，因为它们的值与波场的分布紧密关联。尽管测量点数量少，似乎不足以对波场进行采样，但是共振频率信息对于获得样品的压缩率和密度是冗余的。实际上，在两个位置进行测量足以给出校准参数以及样品的压缩率和密度。但是，较大的A值更好，因为高A值体现更高的灵敏度和反演压缩率的准确性。测量频率增加有助于获得稳定的反演结果。因此，在实际实验中，可以在最高共振频率附近的多个频点进行测量，并用于压缩率的反演。为了检查与反演方法相关的整体误差，使用了3个参考样本和测试样品的所有共振频率。测量点的选择是在实际实验中进行的，这将在下一部分中进行描述。

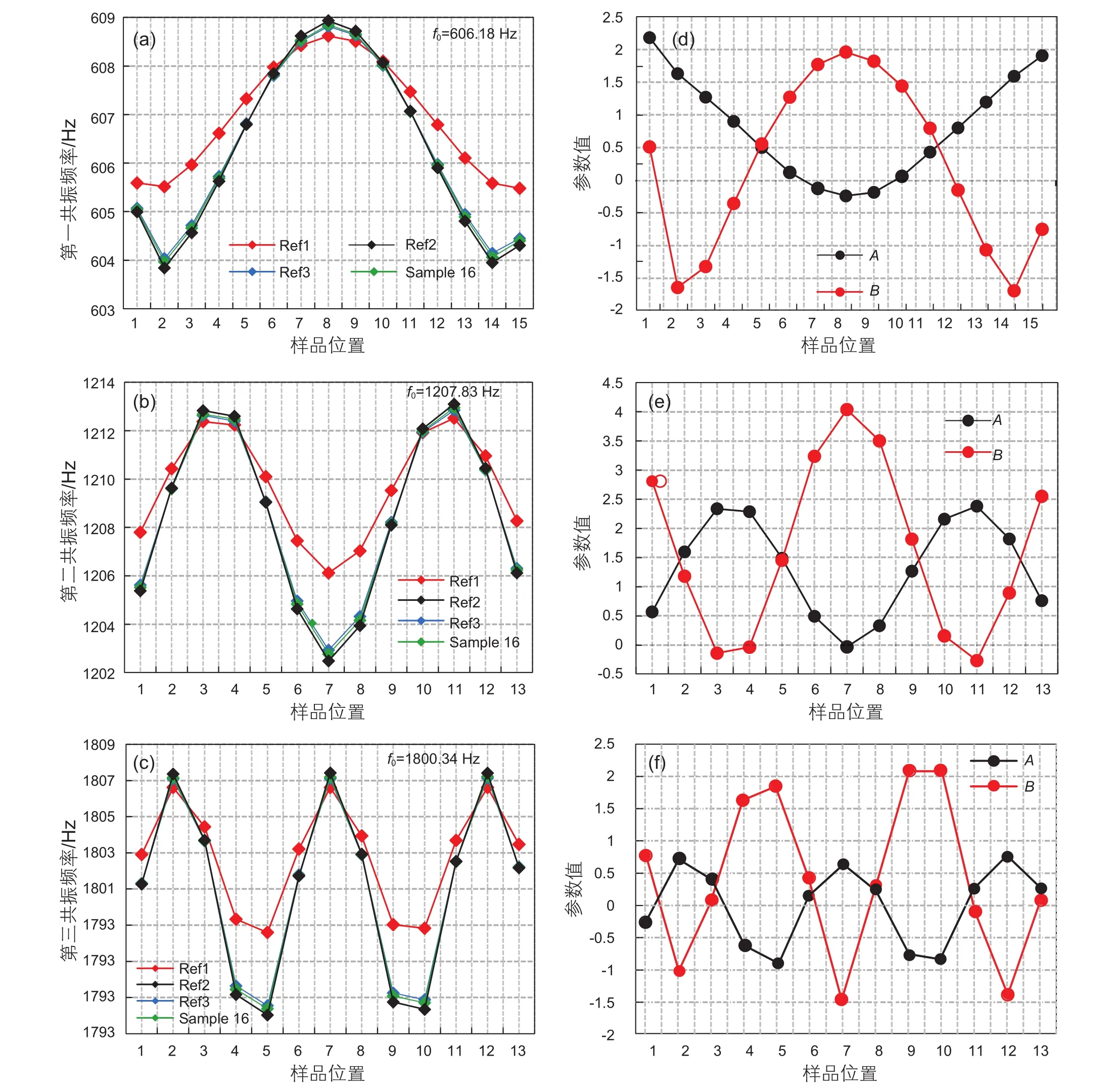
图2 样品#16在三个模拟共振模式下的共振频率(a-c)以及对应频率下反演的校准参数A和B的值(d-f)(注意，不同的共振模式，样品位置不同)Fig. 2 The resonance frequencies (a-c) of sample #16 in the three simulated resonance modes and the values of calibration parameters A and B (d-f) inverted at the corresponding frequencies (Note that different resonance modes have different sample positions)

我们利用3个参考样品和测试样品的所有模拟共振频率，将所有16个假想样品在600 Hz，1200 Hz和1800 Hz的压缩率和密度进行了反演。对于所有三种共振模式(图3a，3b)，样品的压缩率或体积模量都显示出与真实值的偏差很小，随机分布的误差大多在±5%之内(参见表2)，这表明扰动方程对于第二阶和第三阶共振模式也是有效的。假想样品的压缩率和密度的误差主要是由于A和B的估计误差以及从模拟中获得的共振频率的误差引起的。A和B的估计通常需要两个标准样品的共振频率才能满足方程式(1)。但是，由于方程式(1)中定义的压力场的属性随不同的样品而变化，因此会产生一定程度的误差。因此，估计值A和B实际上是在标准样品之间平均的。在实际实验中，我们选择了3个参考样品而不是两个，一个固体铝，一个固体树脂和一种混合固体材料。这可以提高A和B值的准确性，因为可以对3个样本进行平均，其中两个样品的体积模量可与岩石样本相比。无论如何，如数值模拟所示，总体误差水平不会超过±5%。

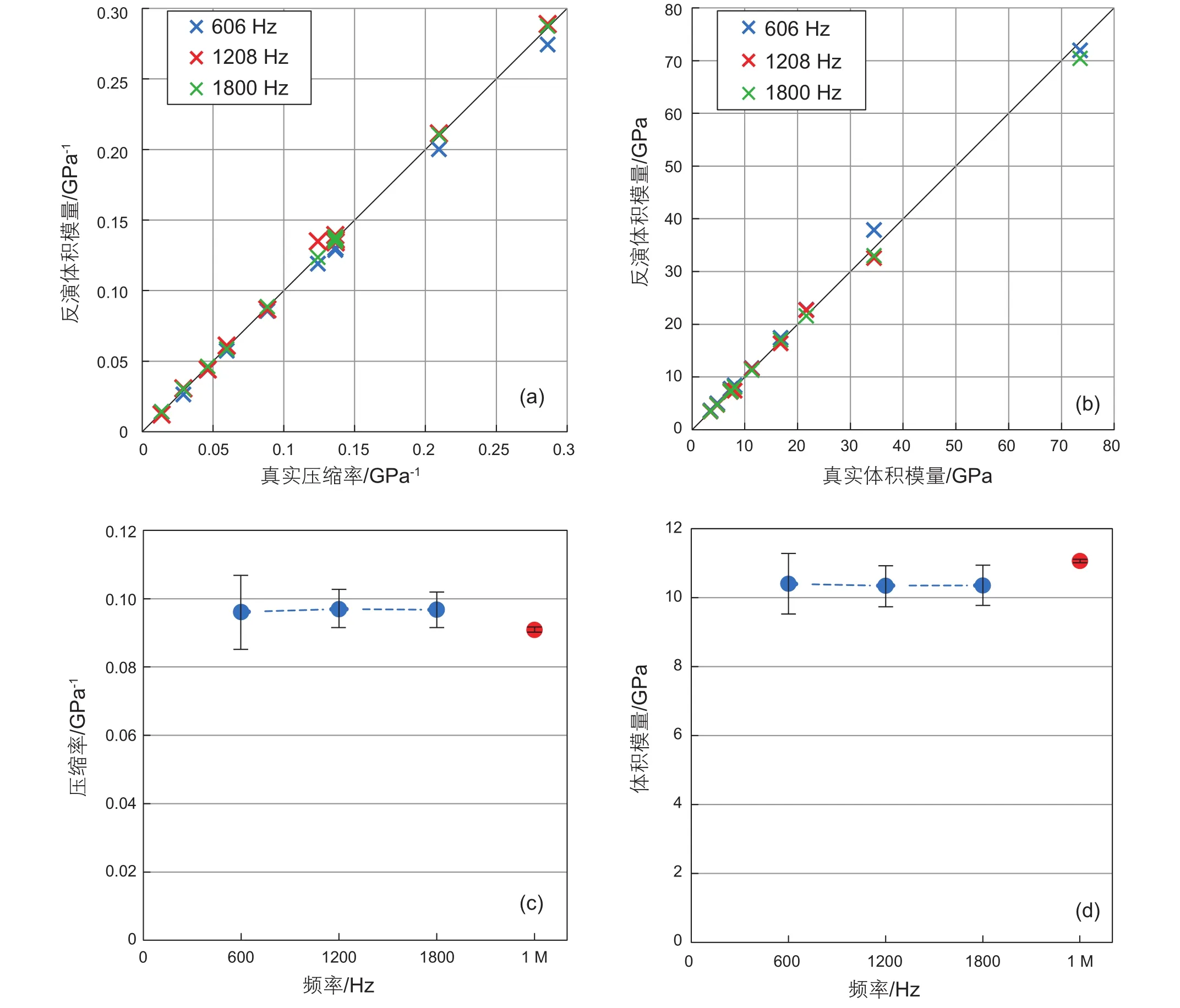
图3 16个假想样品在三种共振模式下反演结果(a)16个假想样品的真实压缩率和体积模量的交会图；(b)16个假想样品的真实和DARS测量的体积模量的交会图；(c)不同共振频率(蓝点)和超声频率(红点)下固体样品的压缩率的变化；(d)不同共振频率(蓝点)和超声频率(红点)下固体样品的体积模量的变化(注：误差棒显示了几次测量的±标准偏差)Fig. 3 Inversion results of 16 hypothetical samples in three resonance modes (a) The intersection plot of the true compressibility and bulk modulus of 16 hypothetical samples; (b) The intersection of the real and DARS measured bulk moduli of 16 hypothetical samples;(c) Changes in the compressibility of solid samples at different resonance frequencies (blue dots) and ultrasonic frequencies (red dots);(d) Changes in the bulk modulus of solid samples at different resonance frequencies (blue dots) and ultrasonic frequencies (red dots).(Note: Error bars show ± standard deviation of several measurements)

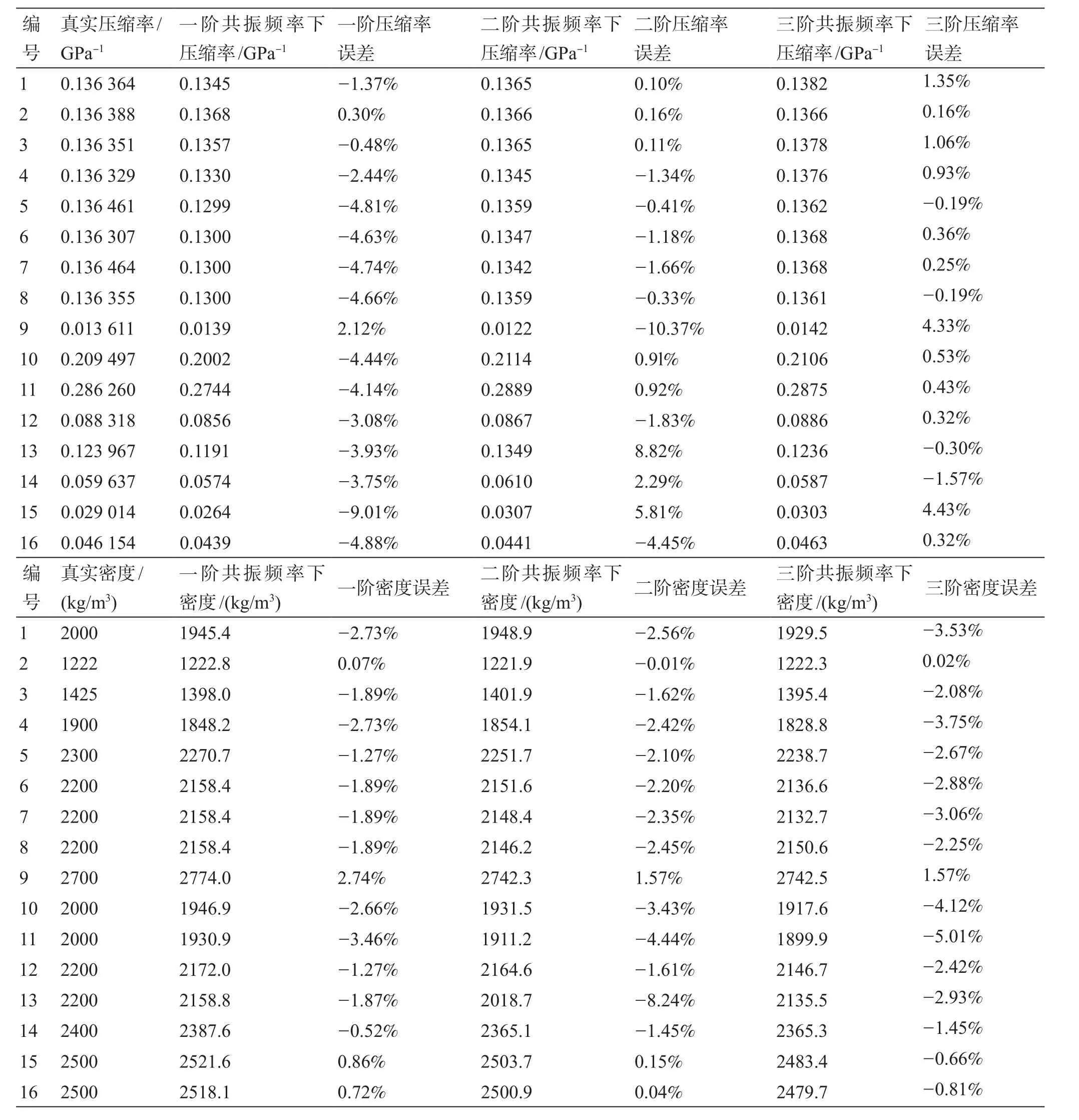
表2 三种共振模式下假想样品从模拟共振频率反演的压缩率和密度的误差Table 2 The compression ratio and density errors of the hypothetical sample retrieved from the simulated resonance frequency in the three resonance modes

为了测试更高阶共振的扰动方程，我们还在真实的DARS测量中使用了由均质材料制成的固体测试样品，以在三个共振频率下获得压缩率(体积模量)。它的体积模量也由超声技术(～1 MHz)测得的密度和速度计算得出。测量结果表明，在不同共振频率下测得的压缩率几乎没有变化，并且在不考虑误差棒的情况下，从超声测量压缩率(～1 MHz)到DARS测量压缩率(～600～1800 Hz)大约增加了 5%(图 3c)。相应地，从DARS结果到超声结果，体积模量增加了约5%(图3d)。压缩率的增加很可能是由与DARS技术和超声技术相关的系统误差引起的。均质和各向同性测试样品的体积模量几乎没有频散。在3个不同的共振频率下测量了3到4次压缩率(体积模量)，误差在平均值的±5%范围内。这些结果表明，如果不存在频散(例如纯固体样品)，则DARS技术将在前三个共振频率下获得几乎相同的结果，从而证实了扰动方程仍适用于更高的共振频率。因此，DARS方法可用于量化一阶和更高阶共振下材料的体积模量。

3 实验结果与分析

我们对7个人造砂岩样品在一阶和高阶共振下进行了DARS实验。这些砂岩是用砂粒和环氧树脂制成的，孔隙度在3.6%～48.7%，并加工成圆柱形状的岩芯。我们测量了这些样品的尺寸，密度，孔隙度，渗透率和超声速度，并列在表3中。这些样品具有简单的孔隙结构，并且孔隙度和渗透率之间存在正相关关系(图4)。砂岩样品用硅油饱和，并且其表面开放以允许在测量过程中流体交换。在实验中，我们使用了3个参考样品，分别是环氧树脂块，铝块以及由石英粉和环氧树脂混合而成的各向同性均匀固体(其性能参见表3)。

在相应扫频范围内，分别获得空腔、3个参考样品和岩石样品的共振频率。人造砂岩没有被密封，因此硅油可以从样品中进出。对砂岩样品在11个连续的位置以1 cm的间隔连续进行每次测量。另外，为了减少压电陶瓷源对波场的影响，在空腔的上半部附近选择这些测量位置(见图1)。

从记录的共振曲线中提取共振频率，该共振曲线显示出压力场振幅随扫描频率的变化。共振频率对应最高振幅。图5a-c显示了针对样品＃2获取的第一阶，第二阶和第三阶共振的共振频率数据。这些共振频率是针对每个共振在不同位置的样品采集的。共振频率随测量位置发生的变化对于第三阶共振模式最大，而对于第一阶共振模式最小。每阶共振的共振频率在中心位置(位置6)处具有最高频率，铝参考样的频率最高，而树脂样品的频率最低，而混合材料参考样(HD-3)介于两者之间。这是由于铝样具有最高的体积模量，而树脂具有最低的体积模量。人造砂岩在中心位置的共振频率位于固体材料和树脂样品之间，表明其体积模量也在其体积模量之间。利用参考样本的这些共振频率，我们可以使用上述最小二乘法对参数A和B进行求逆。在各个位置对应于第一阶，第二阶和第三阶共振的A和B的值在图5d，e中示出。利用样品的共振频率，可以用最小二乘算法求解压缩率和密度。

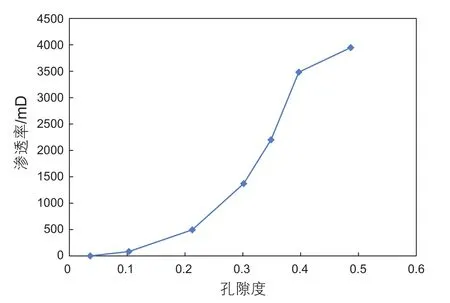
图4 人工砂岩的渗透率随孔隙度的变化规律Fig. 4 Variation of permeability of arti ficial sandstone with porosity

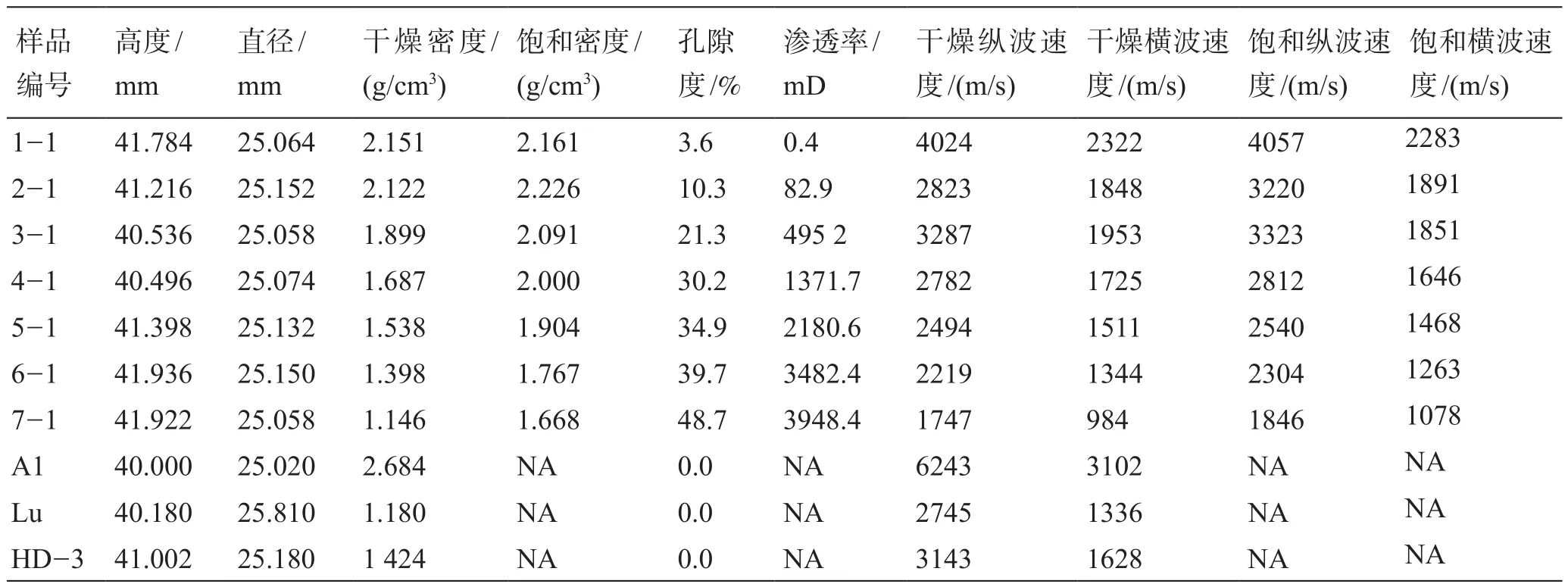
表3 干燥和饱和条件下人工砂岩样品和参考样品的物理性质Table 3 Physical properties of arti ficial sandstone samples and reference samples under dry and saturated conditions

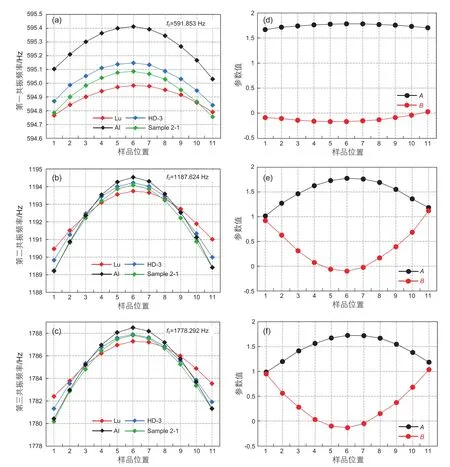
图5 人工砂岩三个共振频率(a-c)以及反演得到的标定参数值(d-f)(注：不同的共振模式，样品位置不相同)Fig. 5 The three resonance frequencies (a-c) of artificial sandstone and the calibration parameter values (d-f) obtained by inversion (Note that different resonance modes have different sample positions)

对各个砂岩样品的测量重复3至4次，以获得一致且可靠的体积模量(表4)。使用最小二乘反演算法将反演的最终平均体积模量如图6所示，并与超声测量(～1 MHz)的体积模量以进行比较。

两种方法测得的体积模量均显示出相对于孔隙度的总体下降趋势。总体而言，在干燥和饱和条件下用超声波测量的体积模量要比在DARS下测量的体积模量要大得多(干燥条件下的样品2-1除外)，这与前人的观测是一致的[31-34]。根据超声波测量结果，孔隙度为10.3%的样品具有异常低的体积模量，与总体下降趋势相差较大，可能是与砂岩矿物组分差异或颗粒尺寸差异有关，CT图像显示样品#2-1的颗粒尺寸是其余样品的4倍(图7)。但是，DARS测量结果中没有这种异常，这揭示了在高频(～1 MHz)和中低频段(600～1800 Hz)的测量之间存在很大差异。这种异常现象表明，对于不同来源和粒度的砂岩，在较低的频带(即DARS频率甚至地震频率)中，可能无法代表超声速度随孔隙度的变化趋势。

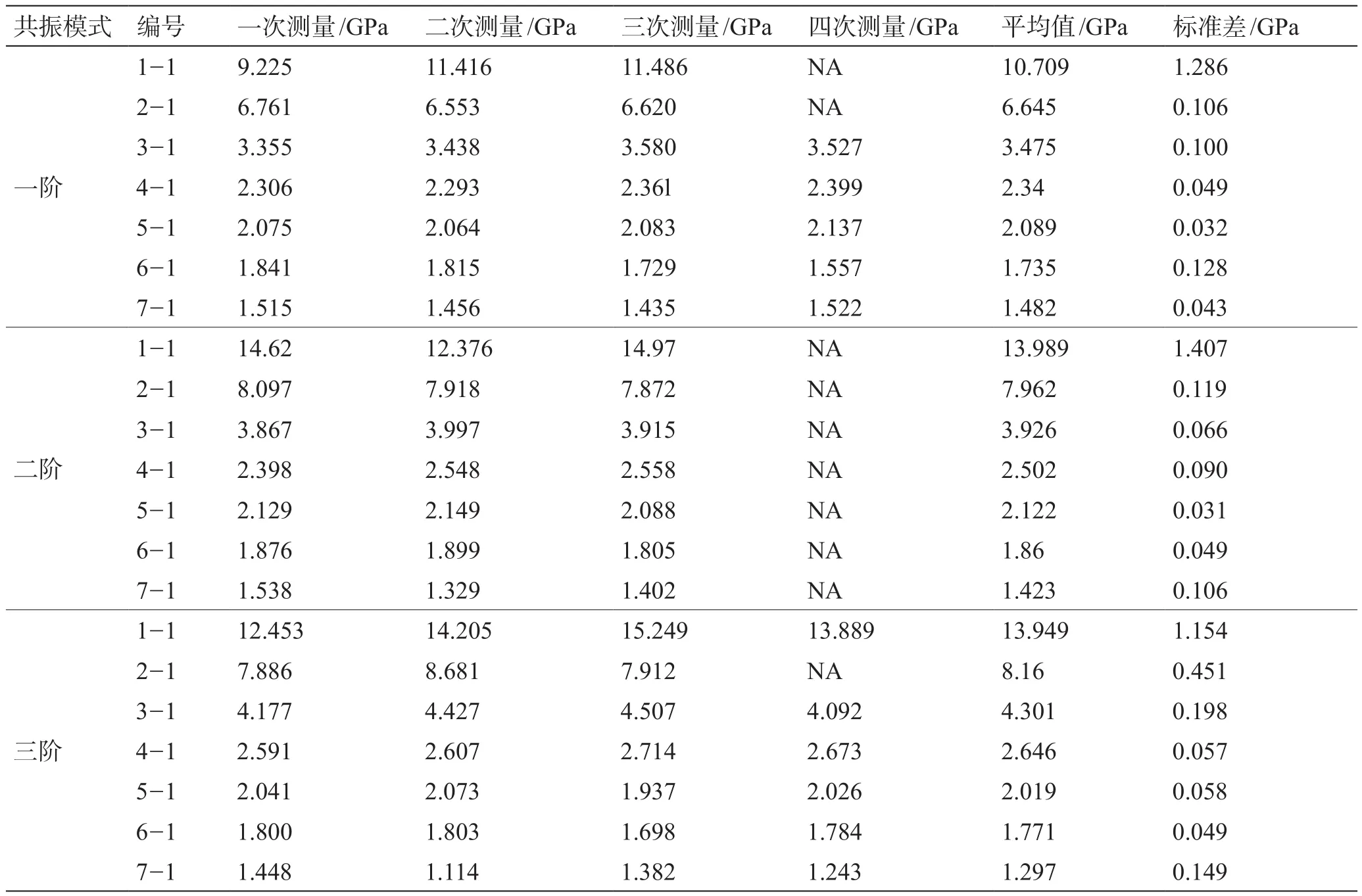
表4 人工砂岩在三个共振频率上的体积模量、平均值和标准差Table 4 Bulk modulus, average value and standard deviation of arti ficial sandstones at three resonance frequencies

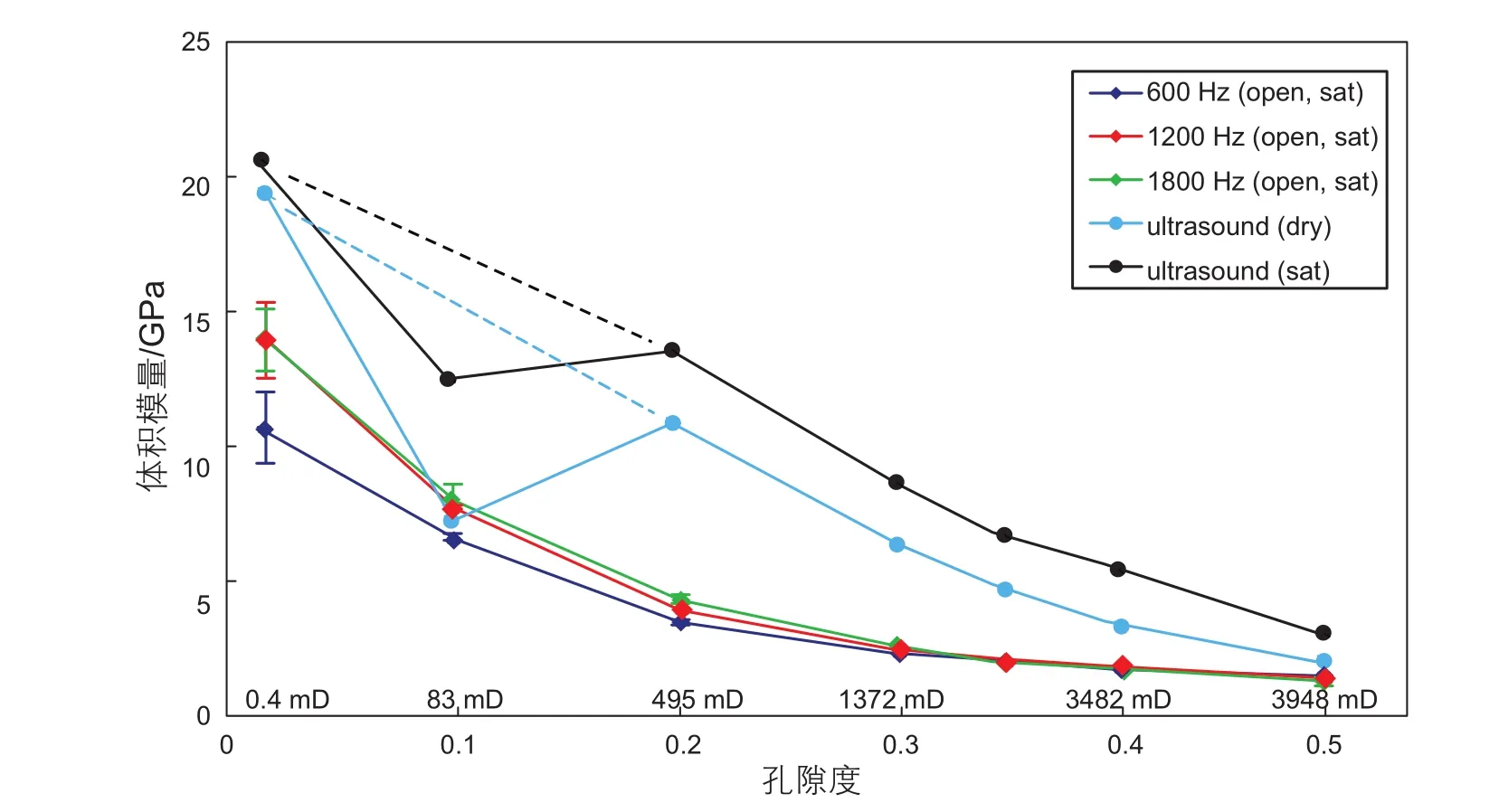
图6 通过DARS测量获得的人工砂岩的体积模量(注：测量误差记为±标准偏差，并标记了样品渗透性)Fig. 6 The bulk modulus of arti ficial sandstones obtained by DARS measurement (The measurement error is recorded as ±standard deviation. Permeability of samples are also marked)

图7 人工砂岩试样(2-1、3-1、5-1)的微米CT图像Fig. 7 Micron CT images of arti ficial sandstone samples (2-1, 3-1, 5-1)

对于在不同共振频率下获得的体积模量，似乎存在一个一般模式，该模式显示第一阶共振结果低于第二阶共振结果，第二阶共振结果又低于第三阶共振结果，尽管对于样品#5而言，这种模式可能无法区分。#5-1、#6-1和#7-1具有很高的渗透率(2181～3948 mD)。与样品#2-1、#3-1和#4-1的显著变化相比，这些样品在三个共振频率之间的体积模量几乎没有变化，而样品#2-1、#3-1和#4-1具有中等到很高的渗透率(83～1372 mD)。样品#1-1的渗透率相对较低(0.4 mD)，并且由于存在较大标准差，很难对体积模量的变化进行量化。但是，该样品也可以遵循体积模量的一般情况，第二阶和第三阶共振频率之间的变化可能相对较小。

4 讨论

数值模拟和实验测试表明，使用DARS在第一阶，第二阶和第三阶共振频率下对体积模量小于20 GPa的样品进行测量是合适的。数值模拟中的体积模量测量误差估计在±5%以内(表2)。在实际实验中，人造砂岩的体积模量的标准差给出了相似的误差水平(参见表4，图6)。但是，在不同共振频率之间测得的体积模量之差大于此误差水平。例如，样品#2-1和#3-1的体积模量分别从～600 Hz增加到～1800 Hz，分别增加了22.8%和23.8%。这表明在误差之上的剩余差异必然是其他因素导致的。我们认为，这些差异代表了体积模量的频散。最有可能的是，不同共振频率下测得的体积模量的差异是实际频散和实验误差的叠加。因此，可以通过DARS技术来测量600～1800 Hz局部频带内的频散。

除样品#2-1外，在干燥或饱和条件下通过超声测量的体积模量比DARS测量值大得多。这似乎很难用现有的理论或模型来解释，因为DARS测量的人工砂岩“太软”。然而，这可以归因于排水条件和样品表面的流体交换的影响。Xu等人[30]也做了类似的观测，他们使用动态流体扩散模型来解释DARS测量的体积模量与超声值之间的巨大差异。

DARS测量本身可以解释频散的原因。在第一阶，第二阶和第三阶共振模式之间，唯一改变的因素是共振频率和腔体内相应的压力场分布。压力波可能会对流体流动特性产生不同的影响。对于无孔固体样品，由于样品内部没有流体流动，共振模式的变化对其压缩率(体积模量)几乎没有影响。相比之下，对于多孔砂岩，由于腔体和样品内部压力场的变化而改变了流体的流动特性，因此在不同的共振模式下压缩率也有所不同。因此，从实验的角度来看，可以确定体积模量的频散是由流体流动引起的，引起频散的物理机理必须与多孔岩石样品中的流体流动特性有关。

频散的控制因素包括非均质性、孔隙流体性质和流动性[5]。在我们的实验中，人造砂岩是由均匀分布的砂粒和简单的孔隙组成；在实验过程中，它们完全饱和。因此，非均质性可能在控制体积模量频散方面发挥较小的作用。另一方面，研究结果表明孔隙度/渗透率与频散之间存在显著的关系。在600～1800 Hz频段，人工砂岩在中低渗透(0.4～1372 mD)时频散较强，在高渗透(3482～3948 mD)时频散较弱。

因此，我们认为渗透率可以控制体积模量在DARS频 段(～600～1800 Hz)， 甚 至 在 超 声 频 段(～1 MHz)的频散。这种现象可以用不同的流体流动性来解释[5]。在这种情况下，高渗透率对应高流动性，使得砂岩中流体孔隙压力平衡所需的弛豫时间较小，从而导致频散特征频率高于共振频率(甚至在超声频率下)。DARS的测量频率属于“低频域”。相反，低渗透意味着低流动性和较长弛豫时间，频散特征频率可能位于DARS测量频带，甚至低于地震频率。实验结果表明，这些人工砂岩落在低频域(高渗透率)或频散域(低至中渗透率)。事实上，高渗透率样品的体积模量频散很小，而中渗透率至低渗透率样品的体积模量频散很大。

5 结论

通过使用DARS的多阶共振频率进行的体积模量测量，我们确定了高阶共振测量的有效性和可靠性。使用三个参考样品代替两个参考样品，我们获得了具有更高准确度的校准参数。通过选择具有较高敏感度的测量位置来改进多点测量的过程，这有助于使用线性最小二乘算法估算可压缩性的准确性更高。该技术扩展了可以使用DARS方法测量体积模量的频段，有助于在局部频段进行直接低频测量。使用此方法结合超声测量方法可以进行频散测量。

利用DARS的一阶，二阶和三阶共振模式，反演了人造砂岩样品在不同频率的体积模量和密度。这些样品的体积模量显示出从低阶共振频率(～600 Hz)到第三阶共振频率(～1800 Hz)的频散。对于具有相对低到中等渗透率的样品，频散较大，而对于具有高渗透率的样品，频散较弱。这种频散差异受渗透率控制，是由于样品孔隙中流体流动性不同，导致不同的样品落入不同的“域”。对于渗透率相对较低或中等的样品，DARS共振频率可能在频散特征频率范围内，因此频散较强。对于渗透率较高的样品，DARS共振频率处于低频范围内，体积模量几乎不随频率发生变化。根据这一结论，在地震和声波测井频率下测得的高渗透率储层岩石的弹性性质可能几乎没有差异。低渗透性的储层岩石在这些频带可能具有相当大的弹性性质差异，从而引起地震与测井获取的储层参数不匹配问题。因此，频散特征频率和强度可能是表征渗透率的指标之一。

综上所述，采用多阶共振频率的DARS测量方法，可以在地震—声波测井频率范围内提供直接的频散数据，对研究岩石的频散机理具有很大的潜力。频散数据还可以用来解释地震和声波频带上弹性性质的差异，为地震与测井匹配问题提供重要的参考依据。由于共振频率主要由共振腔的长度控制，我们可以通过改变腔体长度来进一步扩大共振频率的测量范围。