采用改进的FCM聚类算法进行储层优势通道分级

鲁春华，姜汉桥，李杰，尤诚程，成宝洋，李俊键

中国石油大学(北京)油气资源与探测国家重点实验室，北京102249

*通信作者, junjian@cup.edu.cn

0 引言

砂岩油藏在注水开发过程中，由于油藏平面及纵向非均质性以及注入水的长期冲刷，储层将会形成优势通道，使得注入水无效、低效循环，严重影响开发效果[1-2]。井间示踪剂测试技术被认为是目前识别优势通道最有效、最直接、最准确的方法之一[3-5]。国内外很多学者利用示踪剂解析模型[6-8]、半解析模型[9]、数值模型[10-11]对示踪剂浓度曲线进行拟合解释，反求高渗透层地层参数，以此定量描述优势通道的发育程度。Li等[12]更是根据示踪剂的产出形态，将储层裂缝分为大裂缝、微裂缝和混合裂缝。这些成功案例都是建立在示踪剂产出曲线形态差异大的基础上，使得示踪剂解释结果具有较强的对比性。但是在稠油油藏中，Adams[13]和Miller[14]的研究结果表明：由于油水黏度差别大，稠油油藏的窜流现象更易发生，注入水不仅在平面波及效率低，同时纵向上波及的厚度也非常有限，这使得稠油油藏示踪剂产出曲线多呈抛物线型单峰形状，曲线之间差别小，优势通道发育级别难以判断。 DENBINA[11]等也对稠油的示踪剂产出曲线进行解释，但是并未给出相应的优势通道分级方法。

FCM聚类算法是一种软聚类方法，它运用了模糊数学中的理论，认为大多数事物并非是非此即彼，而是以一种隶属关系确定属于哪一类，该算法对具有模糊属性的优势通道的识别具有天然优势[15]。虽然FCM算法在流动单元分类[16-17]、储层特征提取[18]和油藏开发指标分类[19]等问题有较好的应用，但是FCM算法有个严重的缺陷：聚类数目难以确定，必须手动给出。这使得该算法对于无法确定聚类数目的问题，如本文的示踪剂产出曲线分类，计算准确度较差。

快速搜索和发现密度峰值的聚类算法(Clustering by Fast Search and Find of Density Peaks, CFSFDP)是由Rodriguez and Laio[20]于2014年在Science杂志上提出的新型聚类算法，目前已在数据挖掘[21-22]、电力系统中的离群点检测[23]、无线传感器网络中的能量平衡优化[24]等领域得到很好的应用，石油领域的运用还未见报导。该算法的基本思想是将具有局部极大密度且与其他密度更大点有较远距离的数据点视为聚类中心，通过计算各点的局部密度与更高密度点之间的距离完成数据的划分[20]。但是该算法在确定其他数据属于某一类时，直接用的是距离最短的原则，这使得其在判别优势通道时，没有模糊算法更符合实际情况。

针对上述问题，本文提出了基于CFSFDP算法确定聚类数目，FCM算法进行迭代的改进型模糊聚类算法进行基于示踪剂产出曲线的优势通道分级。该方法既融合了FCM聚类算法对数据样本柔性划分的优势，又弥补了FCM聚类算法需要事先确定聚类数目的不足。通过运用改进的FCM聚类算法对研究区内见剂井浓度曲线进行聚类分析，确定了单峰型浓度曲线之间的差异，并根据示踪剂解释参数确定了适合鲁克沁稠油油藏示踪剂识别优势通道发育程度的分级方法。

1 改进的FCM聚类算法

1.1 确定聚类数

聚类数即初始聚类中心的个数，也就是本文中对示踪剂曲线进行分类的个数。聚类中心的选取原则是应该尽量让其反映整体数据集的密集程度，并且应该被临近点包围，同时临近点和其他聚类中心距离较远。传统的FCM聚类算法的聚类数是人为手动给出，受主观因素影响较大，一旦聚类数选择不当，聚类效果将会很差。同时，要想获得最优的聚类数，只能不断手动调整聚类中心个数。本文利用CFSFDP算法的思想，根据局部密度和与高密度点之间的距离构成的决策图，自动确定聚类数，避免主观因素影响，同时大大节省最优聚类数确定的时间。设待聚类井数(样本数)为n，每口井特征指标数为p，聚类样本矩阵如(1)式所示：

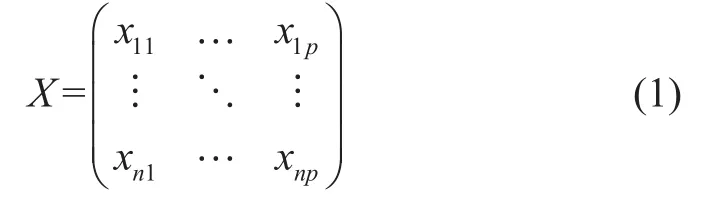
定义见剂井的局部密度ρi为：

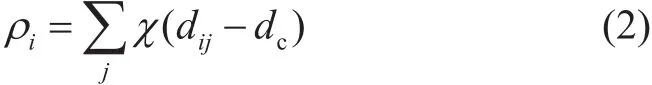
定义与高密度点之间的距离δi，表示的是见剂井i到见剂井j的距离最小值，且有ρj＞ρi，其计算公式见式(3)。

根据计算的每口井的(ρi，δi)，以密度为横轴，距离为纵轴做决策数图，其中密度和距离都较大的点的个数即为聚类数。

1.2 算法的迭代

确定好聚类数目后，需要进行算法的迭代。设将X聚成r类，其目标函数为：

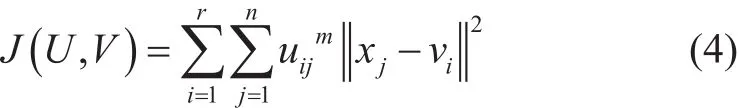
对目标函数求极值可得聚类中心和隶属度。其计算公式见式(5)和式(6)。

式中，m表示模糊加权指数，通常取2，vi表示第i个聚类中心，uij表示第口井对第类聚类中心的隶属度，且有表示第口井的各个指标对第类聚类中心的欧氏距离，i=1,2,…,r，j=1,2,…,n，l表示迭代次数，通过不断迭代的方式更新隶属度uij和聚类中心vi，随着迭代的不断进行，聚类中心逐渐趋于最优，目标函数处于最小值，即所有聚类井到其聚类中心的类内加权误差平方和最小，最终达到的效果是同一类别井之间有最大相似度，而不同类别之间有最小相似度[18]。

1.3 算法流程

改进的FCM算法的具体流程如下：

1) 求出各聚类井之间的欧氏距离dij，并确定截断距离；

2) 根据公式(2)和公式(3)计算各样本的局部密度ρi和高密度距离δi，做由(ρi，δi)数据点构成的决策图，确定聚类数r；

3) 根据[0,1]均匀分布随机数给定初始隶属度矩阵U(0)，令l=1表示第一步迭代；

4) 由隶属度矩阵计算第l步的聚类中心，其中聚类中心由公式(5)确定；

6) 根据公式(4)计算目标函数；

7) 对给定的目标函数终止容限ε＞0，或对于最大迭代步长Lmax，当或l＞Lmax时，停止迭代，否则l=l+1转至第4步。

经过上述的循环迭代止后，当目标函数达到最小时，根据最终的隶属度矩阵U中元素取值确定所有聚类井的归属，当时，可将井xj归于第k类，其中

2 应用实例

2.1 构造区域概况

鲁克沁油田储层平均渗透率537 mD，单一小层平均厚度12 m，埋深2200～3100 m，50 ℃原油黏度12 000～20 000 mPa·s，地下原油黏度 286～526 mPa·s，属于超深层稠油油藏，由于埋藏太深，热采效果不理想，转而采用水驱开发。在长期注水开发过程中，形成了优势通道。但由于油田地处断块发育地带，边底水充足，使得油水井注采对应关系复杂，部分见效油井来水方向难以判定，基于此，开展了井间示踪剂测试。研究区共进行了8井组40口油井示踪剂测试，其中26口油井检测到示踪剂。

2.2 指标选取及聚类

在示踪剂监测的过程中，能直接获取的指标有见剂时间与见剂浓度，这也就是示踪剂浓度曲线。从这条曲线上能获得两方面的信息，一是表示示踪剂流动快慢的突破时间以及峰值时间，并可以通过见剂时间进一步求出见剂速度；二是表示示踪剂采出量多少的峰值浓度与包络面积，其中包络面积的大小代表着回采率的多少。故选取突破时间、峰值时间、见剂速度、峰值浓度以及回采率等参数作为特征指标，见剂井数为样本数n，构成样本矩阵。在聚类之前，首先需要将选取的聚类指标进行Z-score标准化，以消除量纲的影响，数据标准化的公式见式(7)。通过计算每口井的局部密度ρ和与高密度点之间距离δ，结果如图1所示，由聚类数为ρ和δ均较大的点，可以确定目标数据的最优聚类数为3，通过聚类中心和隶属度的不断迭代，研究区见剂井最终被聚成3类。聚类原始数据及结果见表1。

其中：是原始数据的均值，σ是原始数据的标准差。

3 结果分析

3.1 聚类效果分析

由于模糊聚类是软聚类方法，聚类井以最大隶属度原则确定属于哪一类，对于一口井而言，其隶属度矩阵是一个r×1的隶属向量，向量元素中的最大值决定着聚类井属于的类别。如果隶属度向量中最大元素值比其他元素值大得多，则说明这口井属于这一类的可能性越大。基于此思想，定义隶属度向量差值表征类间聚类效果的好坏，越大，聚类效果越好。其计算公式见式(8)。

其中：umax表示隶属度向量中的最大元素值，usec表示隶属度向量中的第二大元素值。

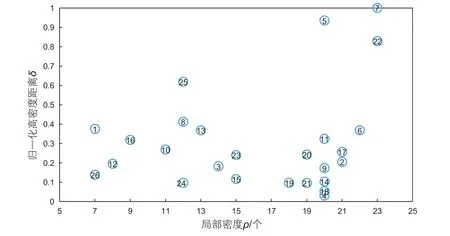
图1 数据决策图Fig. 1 Data decision graph

通过分析所有聚类井的隶属度向量差值，如图2所示，当将研究区所有见剂井聚成三类时，最小的隶属度向量差值为0.019。同时，进一步对比将见剂井聚成两类和四类的隶属度向量差值，结果分别见图3和图4，由图可知，当见剂井聚成两类时，虽然大部分井的隶属度向量差值均大于0.02，但是仍有部分井其值在0.01之间，说明这类井的类间差距较小，聚类效果还需进一步提高。当见剂井聚成四类时，除了第一类井隶属度向量差值较大，其余三类该值均较小，聚类效果很差。由此可知，将见剂井聚成3类是合理的。

图2 聚成三类时隶属度向量差值Fig. 2 The difference of membership vector when cluster equals 3

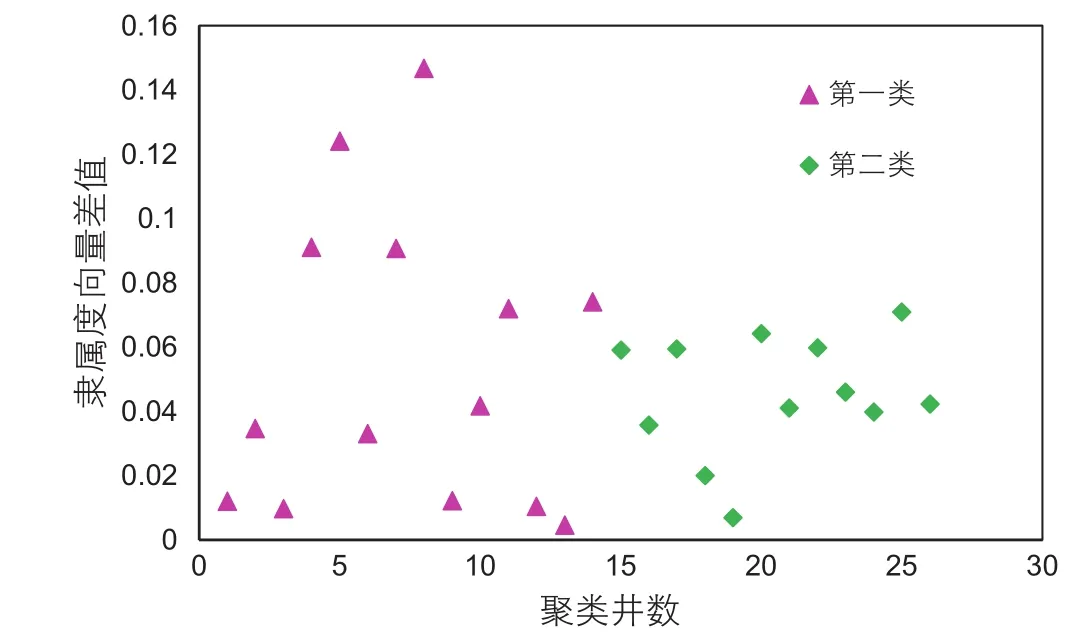
图3 聚成两类时隶属度向量差值Fig. 3 The difference of membership vector when cluster equals 2

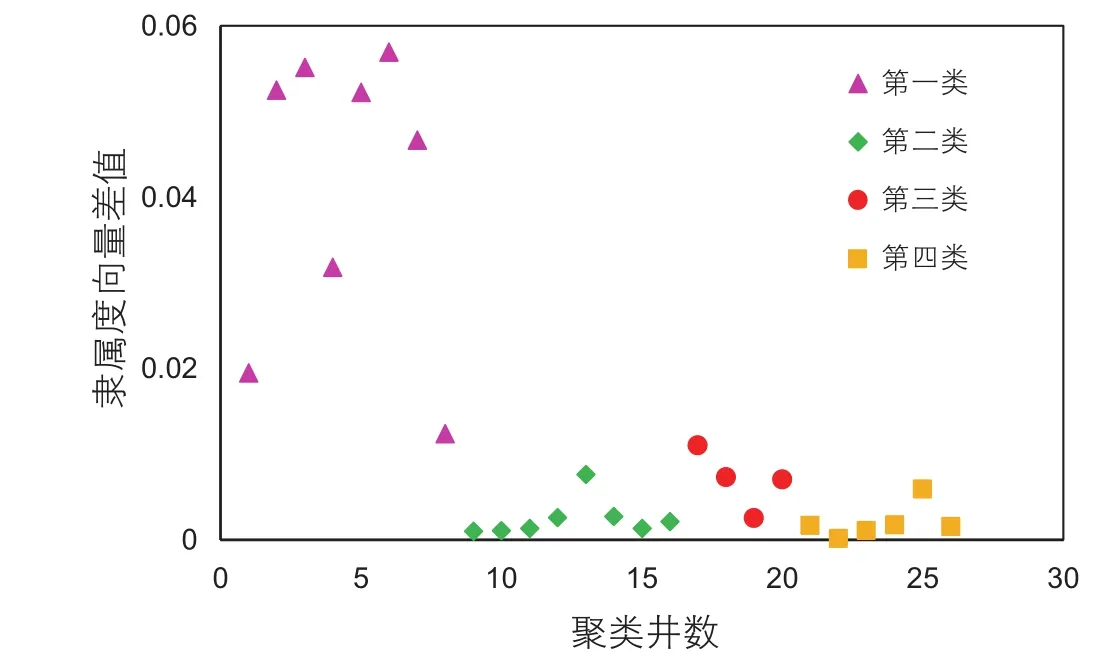
图4 聚成四类时隶属度向量差值Fig. 4 The difference of membership vector when cluster equals 4

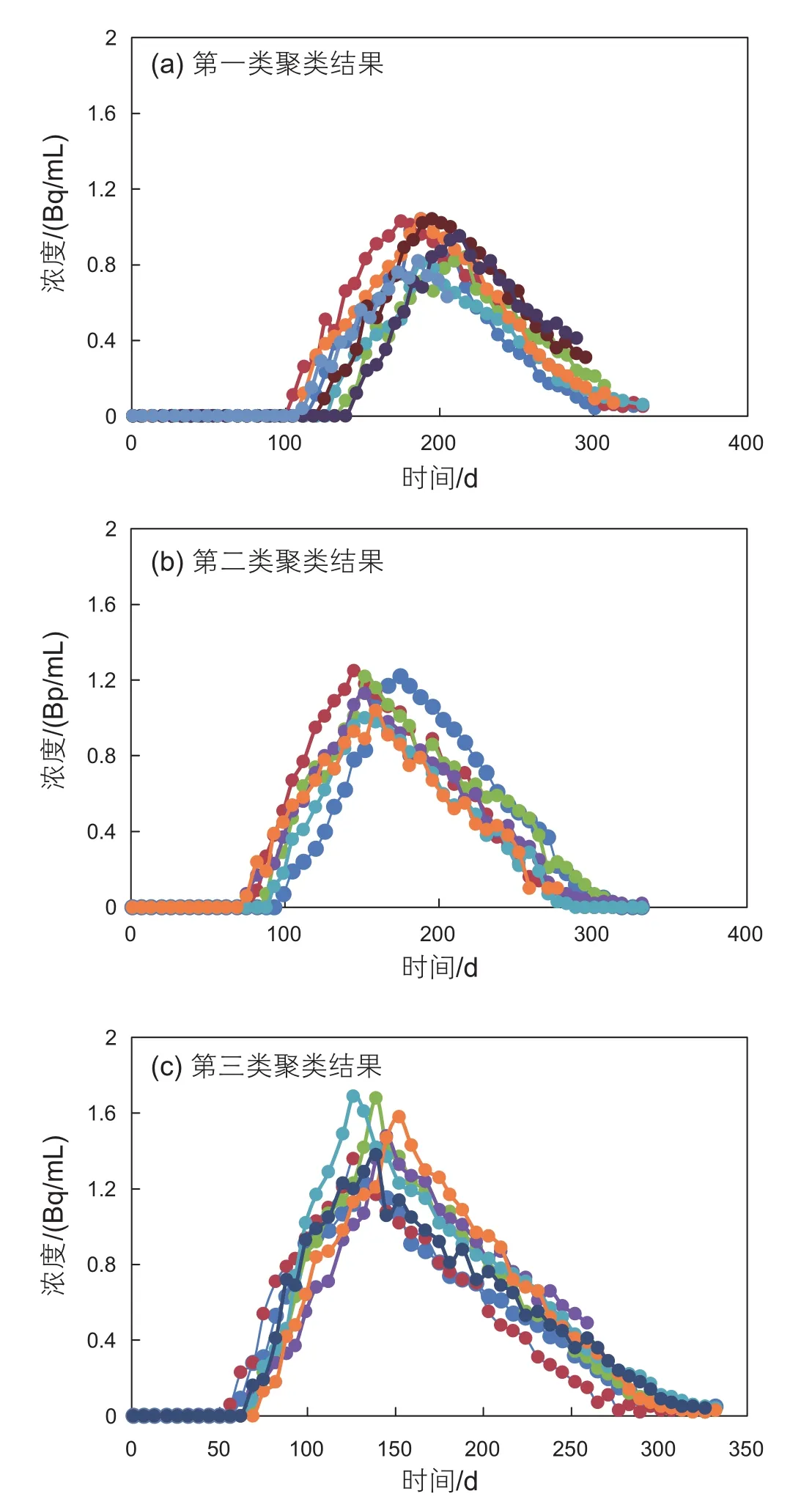
图5 示踪剂浓度聚类结果Fig. 5 Clustering results of tracer breakthrough curves;a. the first kind of clustering results; b. the second kind of clustering results; c. the third kind of clustering results

3.2 曲线形态分类

通过将同一类别井的浓度产出曲线绘制在一起，如图5所示，以进一步验证聚类结果的合理性，发现同一类的井示踪剂浓度产出曲线有相似的见剂时间、峰值浓度，而不同类别的井则差别较大，聚类效果很好。同时基于由Abbaszadeh-Dehghani和Brimg ham推导的考虑示踪剂对流扩散的流动方程[7]，拟合了示踪剂浓度产出曲线，典型井拟合如图6所示，并反求出优势通道层发育厚度及渗透率，定量描述优势通道形成后的储层物性特征，计算结果见表1。

由图5可知，第一类曲线示踪剂见剂时间最晚，基本上在100天以后才检测到示踪剂产出，见剂后浓度上升较慢，从示踪剂解释结果上看，第一类井其高渗层解释渗透率较小，平均渗透率在2180 mD；同时因为地层系数较小，平均地层系数884 mD·m，使得峰值浓度低，曲线与横轴包络的面积小，示踪剂回采率低，曲线总体形态较“矮胖”，优势通道发育程度最低。

第二类曲线高渗层平均解释渗透率6905 mD，平均地层系数2265 mD·m，使得其见剂时间早于第一类井，同时峰值浓度、回采率大于第一类井，优势通道较第一类井发育。

第三类曲线高渗层平均解释渗透率达到了14476 mD，地层系数4162 mD·m，高渗层导流能力强，使得见剂时间最短，相应的见剂速度最快，见剂后浓度很快上升，峰形尖锐；同时峰值浓度最高，相比于第一类和第二类曲线的1.04 Bq/mL、1.22 Bq/mL，其峰值浓度最大可达1.69 Bq/mL，且回采率高，地层系数曲线整体形状较“瘦高”，优势通道发育程度最高。

3.3 优势通道分级

示踪剂在地层中会随着注入水首先从高渗透层突进，由以上分析可知：决定示踪剂见剂快慢的主要是地层的渗透率，决定示踪剂产出量的多少则是地层系数。为此，利用示踪剂解析模型对曲线进行拟合的结果，见表1，进一步分析高渗层渗透率和见剂时间、地层系数和回采率的关系，在半对数坐标下，示踪剂见剂速度与渗透率呈正相关关系，地层系数与回采率在笛卡尔坐标系下呈正相关关系。同时基于示踪剂曲线的聚类结果，以不同类别的井作为分级界限，最终确定当高渗层渗透率小于3259 mD、见剂速度小于1.65 m/d，同时地层系数小于1341 mD·m，回采率小于0.13%视为一级优势通道；高渗层渗透率在3259～8383 mD、见剂速度在1.65～2.17 m/d，同时地层系数在1341～3194 mD·m、回采率在0.13%至0.21%视为二级优势通道；高渗层渗透率大于8383 mD、见剂速度在大于2.17 m/d，同时地层系数大于3194 mD·m、回采率大于0.21%视为三级优势通道。分级结果见图7和图8。

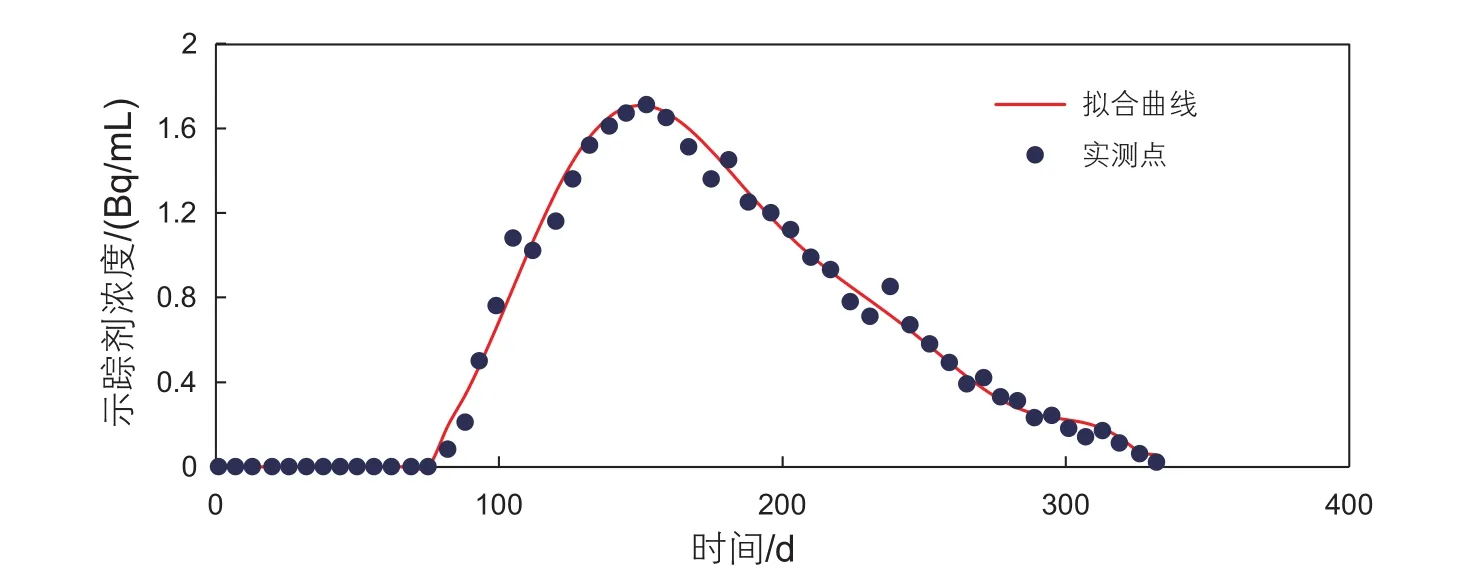
图6 W2-43井浓度拟合曲线Fig. 6 Fitting of tracer breakthrough curve in well w2-43

表1 井间示踪剂参数、洛伦兹系数及聚类结果Table 1 Inter well tracer parameters、Lorentz coefficient and clustering results

3.4 优势通道的表现特征

优势通道的形成有静态地质因素的影响，一般来说，储层非均质性越严重，越易形成优势通道。目前评价非均质的方法有渗透率变异系数、渗透率突进系数、渗透率级差等，但这些数值的计算在理论上都是无界的，不能对储层的非均质程度进行定量评价[26-27]。由于储层砂泥岩交互频繁，本文利用自然电位测井曲线构建洛伦兹系数，定量表征不同级别优势通道在储层测井曲线上的响应特征。将待求深度段的测井曲线值按从小到大排列后得到sp1、sp2…spn，其相应的深度间隔为Δh1、Δh2…Δhn令

图7 见剂速度与高渗层渗透率关系图Fig. 7 Relationship between migration velocity and thief zones permeability

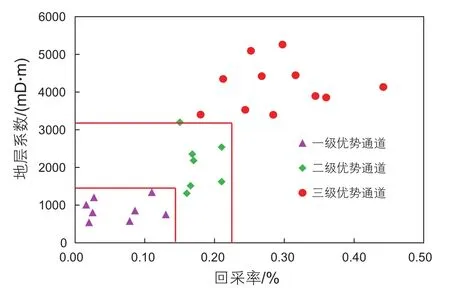
图8 回采率与地层系数关系图Fig. 8 Relationship between recovery rate and formation coefficient

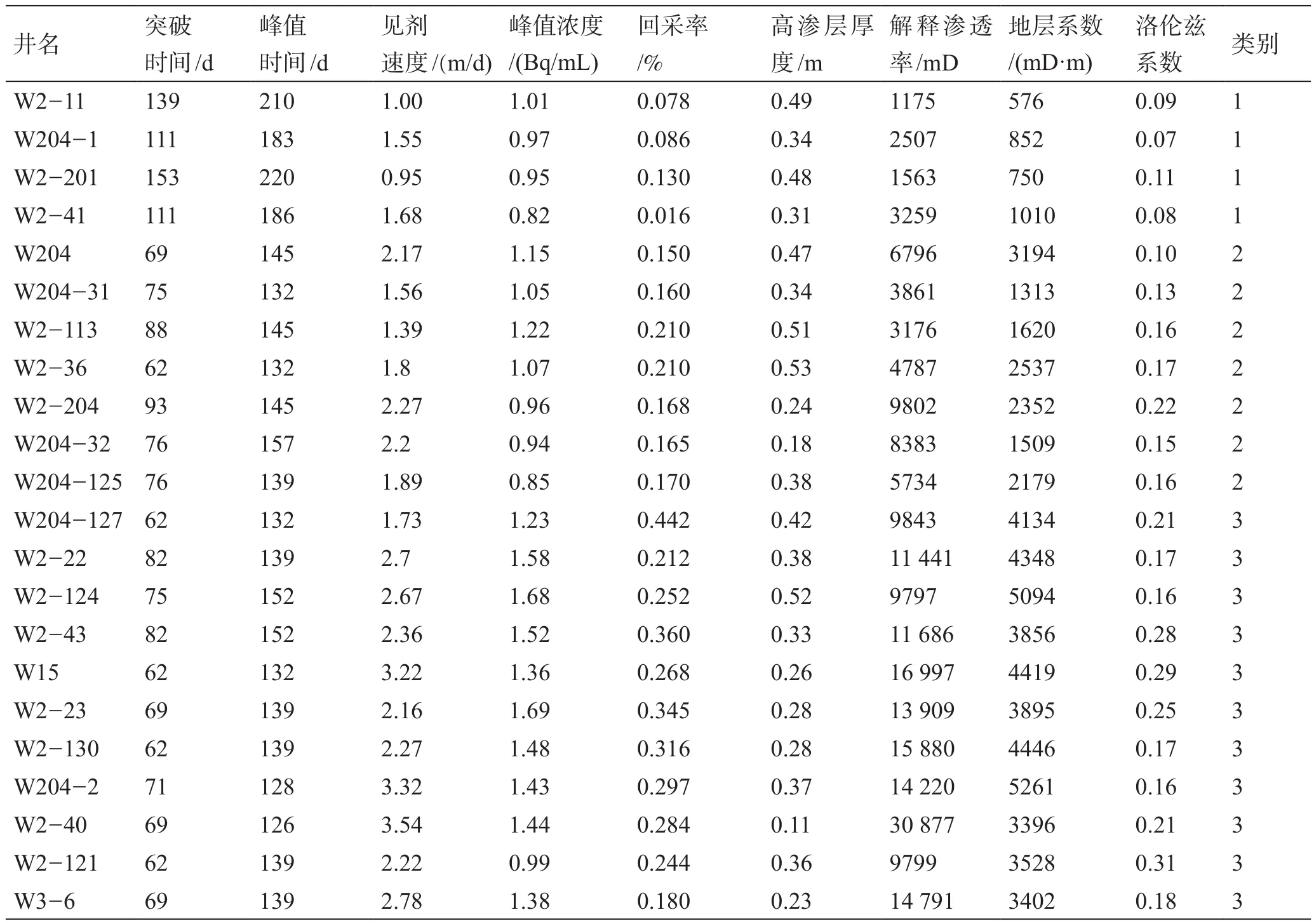
（续表）

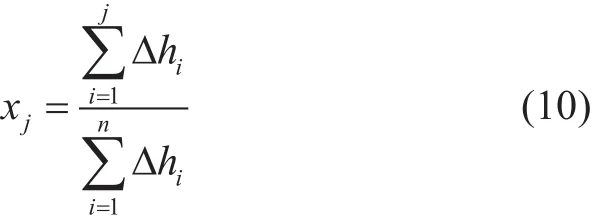
则该段的洛伦兹曲线的函数为：

其中，xj为前j个点的深度间隔累计分布百分比，f(xj)为前个点的测井曲线值的累计分布百分比。洛伦兹系数计算示意图如图9所示，对角线表示绝对均质储层，偏离对角线的面积表示储层的非均质程度，洛伦兹系数Lc计算公式见式(12)，Lc越大，测井值越不均匀，非均质性也越强[28]。

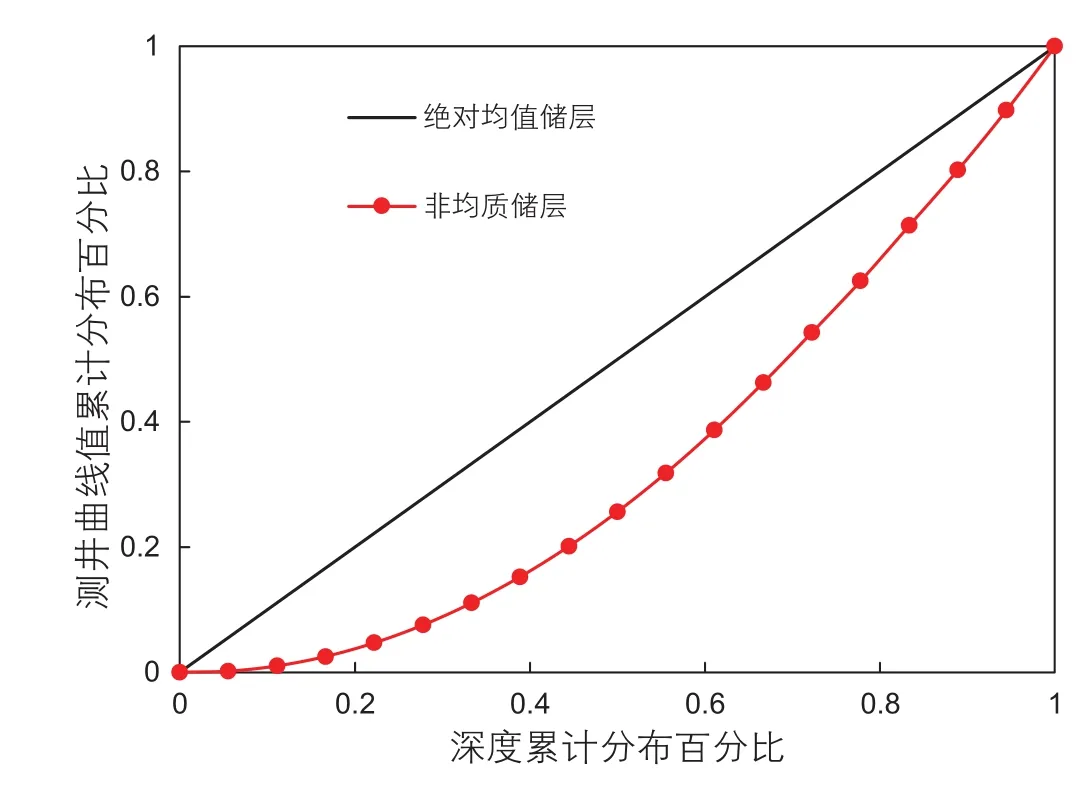
图9 洛伦兹系数计算示意图Fig. 9 Calculation diagram of Lorenz coefficient

分别计算发育三种级别优势通道井的洛伦兹系数，计算结果见表1。一级优势通道井洛伦兹系数分布区间为0.07～0.12，均值0.10；二级优势通道井洛伦兹系数分布在0.1～0.19，均值0.14；三级优势通道井洛伦兹系数分布在0.14～0.29，均值0.2。按照储层非均质性洛伦兹系数评价标准[26]，一级优势通道井属于均质～相对均质储层，二级优势通道井属于相对均质～非均质储层，三级优势通道井属于非均质～严重非均质储层。

同时，分析三种级别优势通道井的生产动态曲线，明确优势通道在开发动态上的响应特征。如图10所示，一级优势通道井在生产期间，含水一直处于相对稳定的水平，同时采出程度较高；二级优势通道井在生成初期，含水率也处于相对稳定的水平，但是在形成优势通道后，其含水率曲线会有明显的上升阶段，影响水驱开发效果；三级优势通道井由于优势通道最发育，其含水率快速上升，同时采出程度最低，严重影响水驱开发效果。

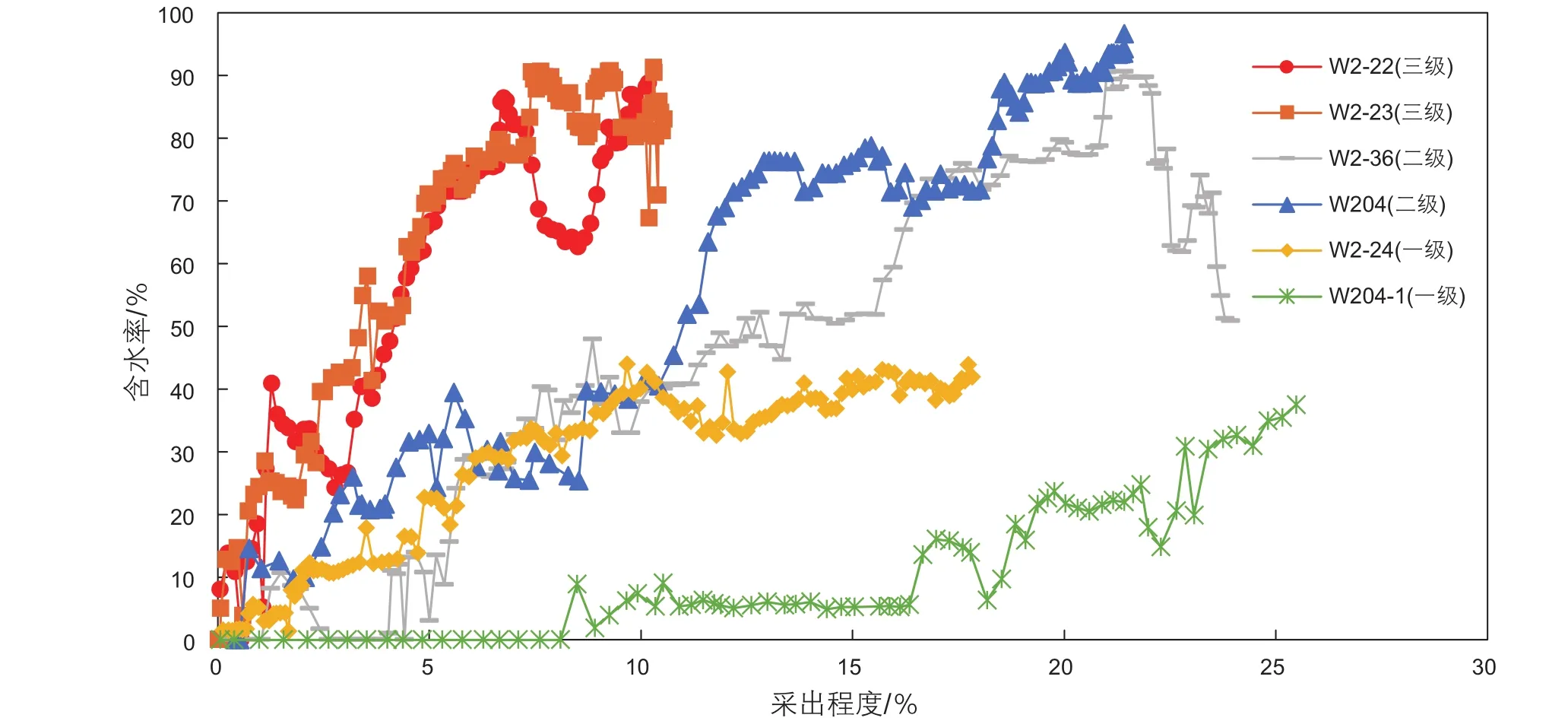
图10 不同类型井生产动态Fig. 10 Production performance of different types of Wells

4 现场验证

由于泡沫对高渗层大孔道和高含水层位的自然选择性，在调剖堵水中扮演着越来越重要的角色。现场对示踪剂测试的2个井组进行了泡沫驱先导性试验，试验井中一级优势通道井有2口，二级优势通道井3口，三级优势通道井5口。以含水率差值△fw和日产油量差值△Qo分别表征含水率降低程度和增油量，见图11。分析发现，井周围储层优势通道越发育，泡沫驱效果越好，相应的含水率降低幅度越大，日产油量增加越多。具体的未见剂井、一级、二级、三级优势通道井含水率降低值分别为6.23%、17.65%、47.55%、51.05%，日产油量增加值分别为0.68 t/d、1.55 t/d、7.66 t/d、9.27 t/d。

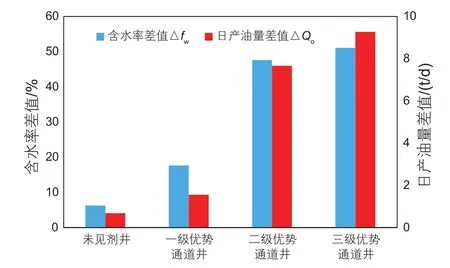
图11 不同类型井泡沫驱效果分析Fig. 11 The effects of foam flooding in different types of Wells

这主要是因为进行泡沫驱时，泡沫首先进入流动阻力较小的优势通道层，并且由于优势通道层含油饱和度低，泡沫稳定性好，更容易在其中堆积，达到封堵高渗层的效果。而随着泡沫占据优势通道层，产生的贾敏效应会增大流动阻力[29]，当流动阻力增加到超过小孔道中流动阻力后，泡沫便越来越多地流入中低渗透层，但中低渗透层往往含油饱和度较高，泡沫中的表面活性剂分子与油中的极性分子进行交换，导致泡沫极易破裂。破裂后的泡沫释放出的氮气不溶于油，在重力分异作用下会进入到构造高部位并不断聚集，形成次生气顶，起到驱油的效果[30,31]。所以，对于优势通道越发育的井，泡沫驱的效果越好。这也进一步验证了分类的正确性。

从现场验证的结果中也给治理稠油油藏的优势通道带来一定的启示：对于示踪剂见剂速度快，回采率高的井，使用泡沫驱将有效改善油田开发效果，对于见剂速度比较慢且回采率不高的井，采用泡沫驱进行调剖堵水效果一般，此时可以考虑其他更加经济有效的措施来改善开发效果。

5 结论

(1)改进的FCM聚类算法能够自动确定待聚类样本的聚类数，避免了传统的FCM聚类算法需要人为指定聚类数的不足，使得其对稠油油藏单一抛物线型示踪剂产出曲线聚类问题有更好的适应性，同时现场的泡沫驱效果分析也验证了分类结果的正确性。

(2)优势通道的发育级别可以通过拟合示踪剂浓度曲线而得到的地层系数和渗透率来定量表征，优势通道越发育，其解释渗透率和地层系数越大，反映在浓度曲线上则是见剂速度和回采率的不同。

(3)影响优势通道发育程度的内因是储层的非均质性，可以通过计算测井曲线的洛伦兹系数定量表征储层非均质性对优势通道形成的影响，结果表明：洛伦兹系数越大，储层非均质性越强，发育优势通道的可能性越大。