基于自适应小波阈值与曲波变换的SAR图像去噪

杨 哲, 邵哲平,b

(集美大学 a.航海学院； b.船舶辅助导航技术国家地方联合工程研究中心， 福建 厦门 361021)

在图像的采集、获取和传输过程中，都会不同程度的受到可见和不可见的噪声“污染”，合成孔径雷达(Synthetic Aperture Radar, SAR)也不例外。为得到清晰的图像，需进行去噪，其目的是尽可能在保留原图像的基础上去除噪声。不同于普通可见光图像被加性噪声所污染，在各种主动成像系统中，如SAR、激光或者超声成像，待恢复的信号往往被乘性噪声所污染。而自适应小波阈值和曲波变换都是针对于加性高斯噪声[1]，该方法应用的前提是将乘性噪声转换为加性高斯白噪声。

目前，对SAR图像去噪的方法包括基于相干斑抑制、背景杂波抑制的方法和基于目标增强的方法。[2]基于相干斑抑制和背景杂波抑制的算法主要包括空间域滤波和频率域滤波2种。其中:空间域滤波[3]是以像元与周围邻域像元的空间关系为基础，通过卷积运算实现图像滤波的一种方法，由于大尺度局域窗会造成边缘模糊，小尺度局域窗会残留较多噪声，因此，会出现抑斑不充分的问题；近年来应用于频率域滤波中的小波变换能较好地解决相干斑抑制的问题，很多学者已在小波域提出很多算法，本文将基于小波阈值和曲波变换提出一种去噪算法。

1 小波阈值去噪

1.1 小波阈值去噪原理

L.Donoho和I.M.Johnstone提出小波阈值去噪算法，该算法的基本思想是：一个含噪信号在进行小波去噪时，经过多层分解后信号小波系数的幅值大于噪声小波系数的幅值，如果设置合理的阈值，就可完成去噪。[4]该算法计算十分简单且视觉效果好，还能有效的保留信号的边缘信息。

小波阈值去噪算法的核心有信号的分解、阈值函数的确定和信号的重构等3部分。信号分解和重构的过程就是小波变换和小波逆变换。小波变换是所有小波域算法的基础，小波变换的实质是原信号与小波基函数的相似性，可将原信号通过相应的小波系数代替，通过对小波系数进行相关阈值的操作以达到去噪的目的。

小波变换实质上是一种以很小的“波”函数表达描述信号，小波变换解决很多傅里叶变换不能解决的难题。[5]小波变换有连续小波变换和离散小波变换2种典型的概念。连续小波变换定义为

(1)

式(1)中：Ψ(ω)为小波基函数φ(x)的傅里叶变换函数;a,τ∈R,a>0,a为伸缩因数，其作用是对基本小波函数作伸缩，τ反映位移，其值可正可负。

在实际的应用中，图像去噪变换算法都是通过计算机实现的，必须对连续小波变换进行离散化处理。离散化处理是针对平移因数τ和伸缩因数a。

离散化处理：

(2)

假设当a0=2,τ0=1时,小波变换为二进制离散小波变换。其定义为

tDWx(m,n)≤f(x),Ψm,n(x)≥

(3)

通过小波变换和小波逆变换就可实现信号的分解与重构。

小波阈值去噪中最重要的是确定阈值函数和阈值。所谓小波阈值函数就是当信号的小波变换系数大于或等于设定阈值时，如何对信号进行处理的依据，小波阈值函数的构造决定去噪质量的好坏。目前，国内外常用的阈值去噪函数有硬阈值去噪函数、软阈值去噪函数[6]、改进的软阈值去噪函数、半软阈值去噪函数和改进的小波阈值去噪函数。国内外常用的小波阈值有VisuShrink算法[7-9]、SUREShrink算法[10]和BayesShrink算法[11]。在这些阈值中，VisuaShrink算法给出的阈值计算简单，但其趋于“过扼杀”小波系数，在图像重构时会发生较大的误差；BayesShrink算法给出的阈值虽然与图像尺寸无关，但随着图像尺寸的增大，较大的噪声系数会被保留下来，使误差增大；SUREShrink算法阈值效果最优但求解过程十分复杂。

1.2 自适应小波阈值去噪算法

在小波阈值去噪发展的过程中，阈值函数和阈值的确定都在不断的优化。阈值函数从硬阈值改进到半软阈值函数等，使小波系数不会出现“突变”的情况，小波系数的变化十分平滑，避免图像出现伪吉布斯现象；阈值从传统的“一刀切”到针对不同的尺度选取不同的阈值，能使阈值的确定适应需要处理的图像，可使去噪更加精确。而这些算法都无法满足智能化去噪的要求，本文将提出一种自适应的阈值去噪算法，可针对不同的像素点确定出适合的阈值，使去噪效果更好。该自适应小波阈值去噪流程见图1。

图1 自适应小波阈值去噪流程

图1中图像去噪的过程可表述为

1) 输入图像，初始化参数值，R为窗口大小，a为小波缩减系数，b为对局部阈值的调整系数。

2) 根据小波分解第一层对角线HH1子带系数估计图像噪声方差δ。

3) 利用小波变换分解图像。

4) 求取每个子带中各像素点小波系数附近的能量E。

5) 确定局部阈值为

λj=4×δ2×logR

(4)

阈值函数为：当某像素点小波系数的能量大于等于b倍的局部阈值时，该阈值化小波系数结果为

(5)

6) 对去噪后的小波系数进行小波逆变换，重构图像。

2 曲波变换

2.1 曲波变换原理

2.1.1连续曲波变换

连续曲波变换和小波变换、Ridgelet变换一样都属于理论的范畴之内，采用信号与基函数的内积以实现信号的稀疏表示。那么，Curvelet为

Cj,l,k=〈f,φj,l,k〉

(6)

式(6)中:j为尺度;l为方向;k为位置;f为原信号;φ为曲波函数。

Curvelet变换在频域内实现，在二维空间中，x为时域内的变量，ω为频域内的变量，频域内极坐标用γ和θ表示。[13]综上可推导式(1)为

C(j,l,k)=〈f,φj,l,k〉=

(7)

2.1.2离散曲波变换

离散变换是以笛卡尔网格的数据为输入，以1组系数为输出。连续曲波变换并不适合于笛卡尔阵列，因此，将该定义为笛卡尔形式的定义，即以同心方形替代同心圆，以剪切替代旋转。以笛卡尔坐标系下f[t1,t2],(0≤t1,t2≤n)为输入，Curvelet变换的离散形式为

(8)

2.2 增强型Curvelet变换图像去噪算法

在图像处理过程中，图像边缘是曲线状而非直线，曲波变换可对含有线或面奇异性的高维函数进行稀疏表示，图像降噪效果比较好。本文将采用增强型Wrap算法完成图像去噪的过程。[14]其变换算法流程见图2。

图2 增强型曲波变换算法流程图

增强型Wrap算法去噪的主要过程如图2所示，其过程细节可表述为

1) 构造均值为0，方差为1的高斯白噪声，对其进行二维逆快速傅里叶变换和转换快速傅里叶变换。然后进行曲波变换，得到对应每一尺度系数标准差的估计值σj。

2) 对含噪图像进行正循环平移(平移范围取为1)。

T=K×σ×σj(K=2.2,2.5)

(9)

5) 对3)和4)中的有关系数进行迭代运算和逆循环平移运算，最后重构图像得到降噪后图像。

3 曲波变换与自适应小波阈值融合去噪

小波阈值去噪对于点奇异性的处理比较好，但对线奇异性的表现较差。曲波变换去噪对线奇异性表现良好，对于一幅图像，其同时存在点奇异性和线奇异性的可能性比较大。因此，本文提出将2种算法进行融合，这样对于图像的去噪效果是十分有效的。[15-16]

该算法的去噪过程是曲波变换和自适应小波去噪的融合，见图3。其具体步骤为

1) 定义匹配阈值T，定义权系数ω。

2) 输入自适应小波阈值去噪后图像、曲波变换去噪后图像。

3) 分别计算2幅图像的相应分解层上对应局部区域的“能量”E，计算2幅图像对应局部区域的匹配度。

4) 定义融合规则：若匹配度大于阈值，说明2幅图像对应局部能量较接近，可采用加权平均的融合方法；若匹配度小于阈值，说明2幅图像对应局部能量相差较大，可选取局部区域能量较大的小波系数作为融合图像的小波系数。

5) 按照融合规则进行图像融合。

图3 自适应小波阈值和曲波变换去噪融合算法流程

4 试验结果和分析

使用的SAR图像来源于南海研究论坛渚碧岛SAR图像。拍摄时间为2016年11月25日，拍摄地点为北纬10°54′，东经114°6′。通过对256×256像素的图像进行去噪，来验证算法的可行性。

本试验选取ZBDSARH256.png和ZBDSARH256(1).png作为试验图像，自适应小波阈值去噪采取软阈值去噪、半软阈值去噪作为对比；自适应小波阈值去噪时,采用的小波基函数为haar小波，引文经过试验数据证明在采用haar小波时，去噪后图像的峰值信噪比会相对较好。曲波变化去噪，试验环境为MATLAB R2018 a。试验采用信杂比(Signal-to-Clutter Ratio,SCR)作为评判标准，利用背景杂波标准差σB描述背景杂波的均匀变化。信杂比的计算方法为

(10)

式(10)中:MT为目标像素灰度的峰值;MB为背景邻域灰度均值;σB为背景杂波标准差。

4.1 SAR图像自适应小波阈值去噪效果比较

对原始图像进行软阈值去噪、半软阈值去噪和自适应小波阈值去噪后的结果见图3～图10，SCR、σB和峰值信噪比等参数见表1。

图3 原始SAR图像1

图4 图像1软阈值去噪

图7 原始SAR图像2

图8 图像2软阈值去噪

由图3～图6，图7～图10 图像的对比和表1数据可知:利用自适应小波阈值去噪算法对原始图像进行处理比软阈值、半软阈值去噪算法处理过的图像船舶完整度更高，最大程度地抑制噪声，SCR更高，σB更小。SCR更高表明SAR图像船海对比度更高；σB更小表明背景杂波更平滑。

表1 小波阈值去噪不同方法的去噪效果比较

4.2 SAR图像曲波变换去噪效果比较

对原始图像1和图像2进行曲波变换去噪后的结果分别见图11和图12。

图11 图像1曲波变换去噪

图12 图像2曲波变换去噪

4.3 SAR图像去噪融合效果

采用自适应小波阈值去噪和曲波变换去噪后的图像按所提出的融合算法进行融合，得到最终去噪图像分别见图13和图14。σB、峰值信噪比等参数见表2。

图13和图14分别为自适应小波阈值去噪后的图6和图10与曲波去噪后的图11和图12通过融合算法而来，通过非量化的视觉效果来看，融合算法船舶完整度更高，船舶边缘更加平滑。这是因为融合算法不仅解决小波阈值算法只能对“点奇异性逼近的问题，而且优化曲波变换去噪算法只能对“线奇异性”逼近的问题。由表2可知:本文提出的算法船海对比度更高，背景杂波更加平滑，去噪效果更好。

图13 图像1融合效果图

图14 图像1融合效果图

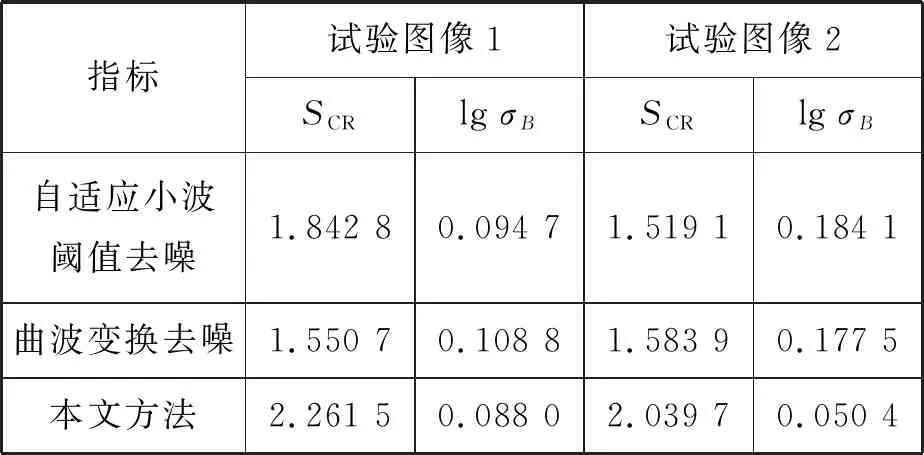
表2 融合算法与单一算法去噪效果比较

4.4 SAR图像去噪效果对比

采用SAR图像的三维网格图来描述背景和目标对比度的变化，使得去噪效果能更直观的展示。本文将对原始图像、自适应阈值去噪后图像、曲波变换去噪后图像以及融合后算法的三维网格图进行对比，说明融合算法的可行性和优越性，见图15～图22。

图15 原始SAR图像1

图16 图像1自适应阈值去噪

图17 图像1曲波变换去噪

图18 图像1融合算法去噪

图19 原始SAR图像2

图20 图像2自适应阈值去噪

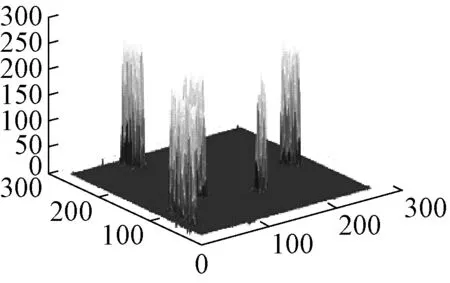
图21 图像2曲波变换去噪

图22 图像2融合算法去噪

由图15～图22可知：图15～图18为图像1的不同去噪效果展示，自适应阈值去噪后图像的噪声被抑制，可发现曲波变换后去噪效果更佳平滑；图19～图22为图像2的不同去噪效果展示，同样可得到图像1的相似结论。从2幅图像融合算法去噪后的三维网格图可知:融合算法结合自适应阈值去噪和曲波变换去噪的优点，去噪后图像目标与背景对比度更高，且图像变换比较平滑。

5 结束语

随着小波理论的深入发展，小波变换和曲波变换仍然是图像去噪领域必不可少的工具。本文首先通过对小波理论和小波阈值去噪的介绍引出自适应的小波阈值去噪算法，然后基于曲波变换提出增强型曲波变换算法。在考虑到小波阈值算法和曲波变换算法的局限性下，提出基于自适应小波阈值与曲波变换的图像融合算法。试验结果表明:相比于传统的小波阈值算法，自适应小波阈值算法去噪效果更好；表2表明融合算法的去噪效果比单一的算法更理想，验证该算法的可行性。