基于复合控制的磁悬浮CMG动框架效应抑制

王舒，郑世强

（北京航空航天大学 仪器科学与光电工程学院，北京100083）

控制力矩陀螺（Control Moment Gyroscope，CMG）是敏捷机动卫星、大型卫星平台、空间站等航天器进行姿态控制的重要执行机构［1-2］，主要由高速转子系统和框架系统组成，通过框架转动强制高速转子改变角动量的方向从而输出力矩，进而调节航天器的姿态［3］。与机械轴承CMG相比，磁悬浮CMG（Magnetically Suspended CMG，MSCMG）具有无摩擦、无需润滑、可通过主动控制实现极微振动等优点，已成为CMG研究的前沿方向［4-5］。

MSCMG中转子径向角位移会随着框架转动而显著增大（动框架效应），使得转子位移跳动量加大，甚至导致磁轴承与高速转子发生碰撞［6］，影响MSCMG系统的稳定性和高速转子的悬浮精度。除动框架效应之外，高速转子的陀螺效应［7］、电流刚度、位移刚度的变化等因素也会影响MSCMG系统的稳定性［8］，因此需要采取有效措施抑制扰动对磁轴承系统的影响，保证磁轴承系统的稳定性和MSCMG输出力矩精度。

对于动框架效应中的可建模扰动，通常采用前馈控制方法进行抑制。文献［9］提出了加速度前馈控制方法，但只解决了转子平动造成的扰动问题，无法解决框架转动形成的动框架效应问题。文献［10-11］提出了基于框架角速率的前馈控制方法，但该方法的补偿效果很大程度上依赖于对象模型的精度。文献［12-13］提出一种基于框架角速率的FXLMS自适应前馈控制方法来减小前馈补偿精度对于对象模型精度的依赖程度，该方法收敛速度快，抗噪声能力强，但因算法非常复杂、计算量大而无法进行实验。霍甲等［6］为了实现实际应用，提出一种简化FXLMS补偿算法，该算法也是基于框架角速率，对动框架效应抑制效果良好，但对模型外的扰动抑制能力有限。所以要提高MSCMG磁轴承的控制精度，除了补偿动框架效应，还需要对不可建模扰动进行高精度抑制，从而提高MSCMG磁轴承整体抗干扰能力。

对不可建模扰动抑制，最早由韩京清教授提出一种基于扩张状态观测器（Extended State Observer，ESO）的自抗扰控制（Active Disturbance Rejection Control，ADRC）方法［14-15］，该方法动态性能好，不依赖模型，且抗扰性和鲁棒性均优于传统PID控制器。丛爽等［16］将ADRC成功应用于陀螺稳定平台，利用ADRC对系统中未建模部分进行观测及补偿，证明了ADRC的可行性和优越性。文献［17］将ADRC和RBF神经网络控制方法相结合，成功应用于磁悬浮控制敏感陀螺的高精度快响应强鲁棒控制，表明可以通过优化ADRC的方式实现对CMG的高精度扰动抑制。以上ADRC方法的成功应用，为解决MSCMG在输出力矩时的不可测扰动抑制问题提供了有益借鉴。

本文从工程应用出发，为了提高磁轴承系统的动态响应与整体抗干扰能力，针对MSCMG的动框架效应和不可测扰动，结合自适应控制与ADRC各自的优点，提出一种基于角加速率自适应前馈控制与ADRC相结合的复合控制方法，并进行仿真分析和实验验证。

1 MSCMG动力学模型

如图1所示，MSCMG由磁悬浮高速转子系统和框架系统两部分组成，每部分又有各自的转子组件和定子组件。高速转子绕自转轴恒速旋转，提供大小恒定的角动量，框架转动带动磁悬浮高速转子系统沿框架轴转动，强制高速转子改变角动量方向，对外输出力矩，进而调整航天器姿态［18］。

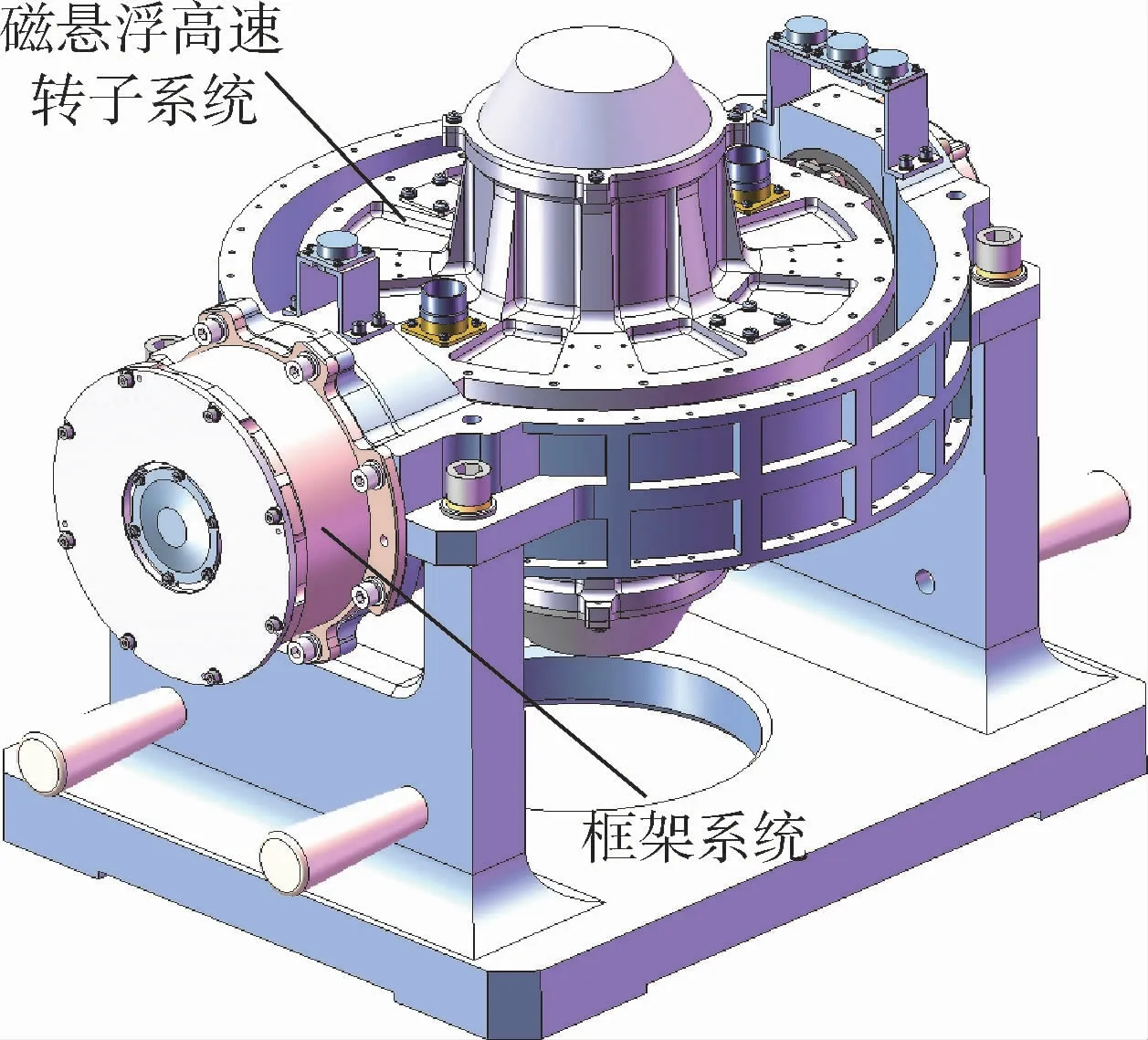
图1 磁悬浮控制力矩陀螺示意图Fig.1 Schematic diagram of MSCMG

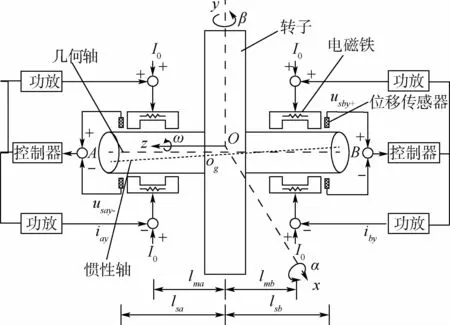
图2 磁悬浮高速转子系统坐标图Fig.2 System coordinate of magnetic levitation high-speed rotor

磁悬浮高速转子坐标系如图2所示，图中，4对径向电磁铁和位移传感器对称分布于转子两端A和B，对应4个通道ax、bx、ay、by。设O-xyz为惯性坐标系，框架坐标系初始状态O-xyz重合，相对于O-xyz绕Oy旋转，定义转角为θ；lma和lmb分别为转子A端、B端磁轴承中心到转子中心的距离，且lma＝lmb＝lm；lsa和lsb分别为转子A端、B端传感器中心到转子中心的距离；x和y分别为转子沿Ox-和Oy-轴的平动位移量；α和β分别为转子绕Ox-和Oy-轴的扭转角。

由文献［1］可知，当框架以角速率θ·转动时，MSCMG的磁悬浮高速转子动力学方程可表示为

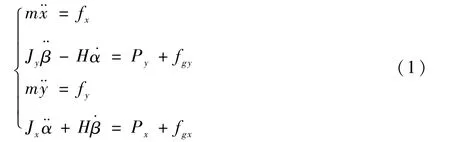
式中：m为转子质量；Jx、Jy为赤道转动惯量，且Jx＝Jy；H为转子角动量；Px和Py分别为沿x轴和y轴方向的磁轴承力矩；˙α为α的角速率（微分），¨α为α的角加速率（二阶微分），以此类推；fx和fy分别为沿x轴和y轴方向的磁轴承作用力；fgx和fgy分别为框架角运动引起的沿x轴和y轴方向的陀螺力矩，可表示为

式中：fax、fbx、fay和fby分别为框架角运动引起的陀螺力矩等效对应4个通道ax、bx、ay、by的扰动力，表示为

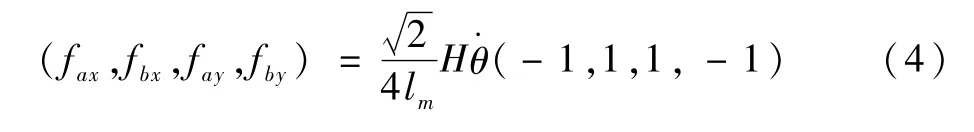
由于对转子不平衡振动已采取加入同频陷波器滤除反馈位移信号中的同频量来实现最小电流控制的措施，动力学模型中未考虑转子不平衡的影响。

2 复合控制策略

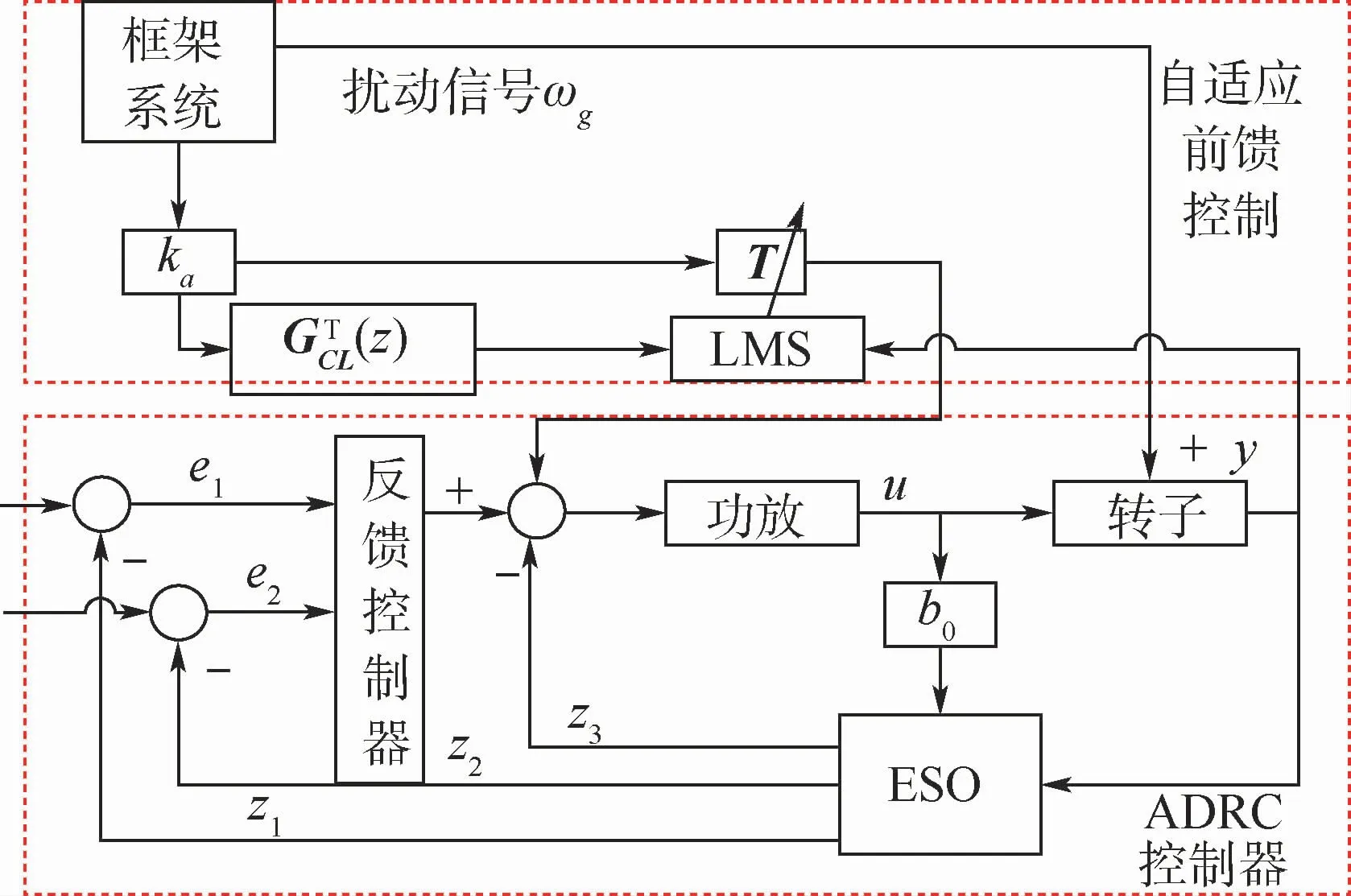
图3 MSCMG磁轴承复合控制方法原理框图Fig.3 Principle block diagram for magnetic bearing composite control method of MSCMG

2.1 自抗扰控制

ADRC控制器如图4所示，主要由ESO、状态误差的非线性反馈律Ki、Kd，以及误差反馈控制

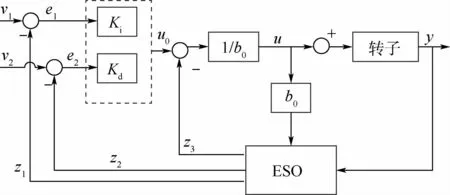
图4 自抗扰控制器结构Fig.4 Structure diagram of active disturbance rejection controller

控制量经过功放驱动磁悬浮轴承线圈，从而实现对系统中扰动的抑制。

2.2 角加速率自适应前馈控制

自适应前馈控制是随着运行环境改变而自动调节自身控制参数，根据扰动或给定值的变化按补偿原理来工作，以达到最优控制的控制方法。本文采用角加速率自适应前馈控制方法对动框架效应进行补偿，系统如图5所示。图中：n1为系统扰动信号；e（n）为转子系统输出值与给定值的误差信号；T为自适应调节权值，根据式（4）可得到的T初始值为

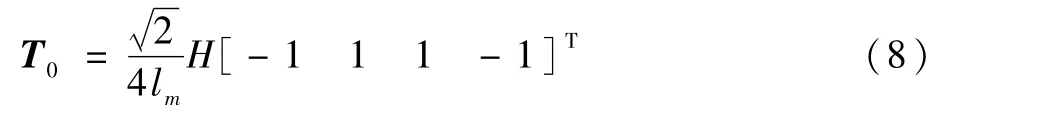
由式（5）可以得到框架扰动环节GRG（s）传递函数为

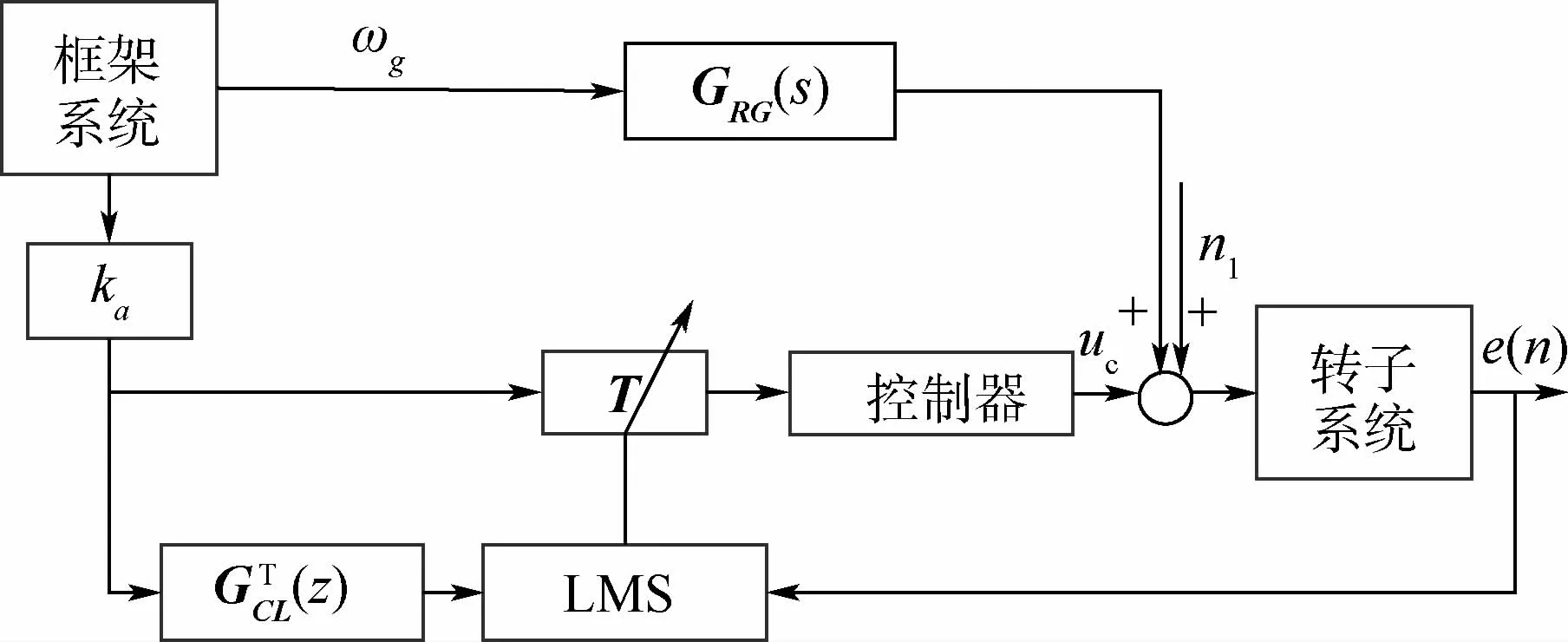
图5 角加速率自适应前馈控制框图Fig.5 Block diagram of adaptive feedforward control module with angular acceleration rate

由于磁悬浮转子4个通道完全对称，则4个通道的ωg（n）和e（n）均相等，即M 等。由式（14）可以分析得出，I－ηM 谱半径小于1且N界的情况下，E［T（n）］一定收敛。由此可设M特征根为λi（i＝1，2，3，4），可以推出E［T（n）］的收

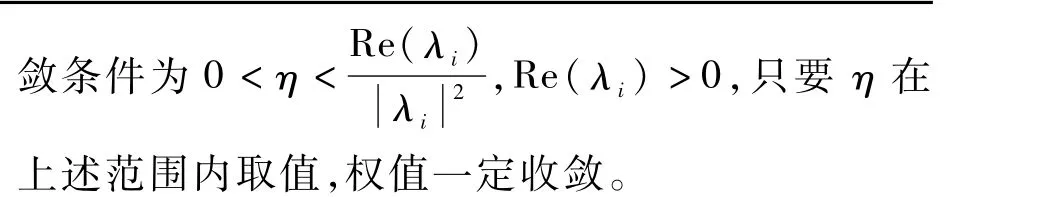
2.3 稳定性分析

由2.1节可知，只要使η值满足收敛条件，自适应前馈权值T总是收敛的，此时角加速率自适应前馈补偿量相当于一个常值，对整个磁悬浮系统的稳定性不再产生影响。对于ADRC，假设系统输出的预定轨迹为v，则真实值与预定值的误差可以表示为

3 仿真校验

为验证本文提出的MSCMG动框架效应抑制方法的有效性，采用MATLAB软件进行仿真研究。设定角速率大小从0°／s经过0.15 s逐渐变到＋15°／s，然后持续0.5 s，再经0.3 s逐渐变到－15°／s。角加速率信号由角速率信号通过不完全微分得到，以该角速率信号作为扰动输入，等效于产生26 N·m的扰动力矩，然后直接作用在磁轴承系统上。

首先对MSCMG磁轴承复合控制的稳定性进行验证，采用不同转速下的根轨迹来判断系统稳定性。图6为转子转频从0变化到150 Hz时的磁轴承系统根轨迹图，根轨迹全部位于坐标系的负半平面，说明磁轴承复合控制系统是稳定的。

图7为基于复合控制的磁轴承系统在工作时，角加速率自适应算法中的权值变化波形。权值初始常值为0.13；t＝1 s后系统接入自适应前馈，权值立即发生变化并在3 s内快速趋于稳定，说明自适应算法运行效果良好，自适应前馈控制运行稳定。

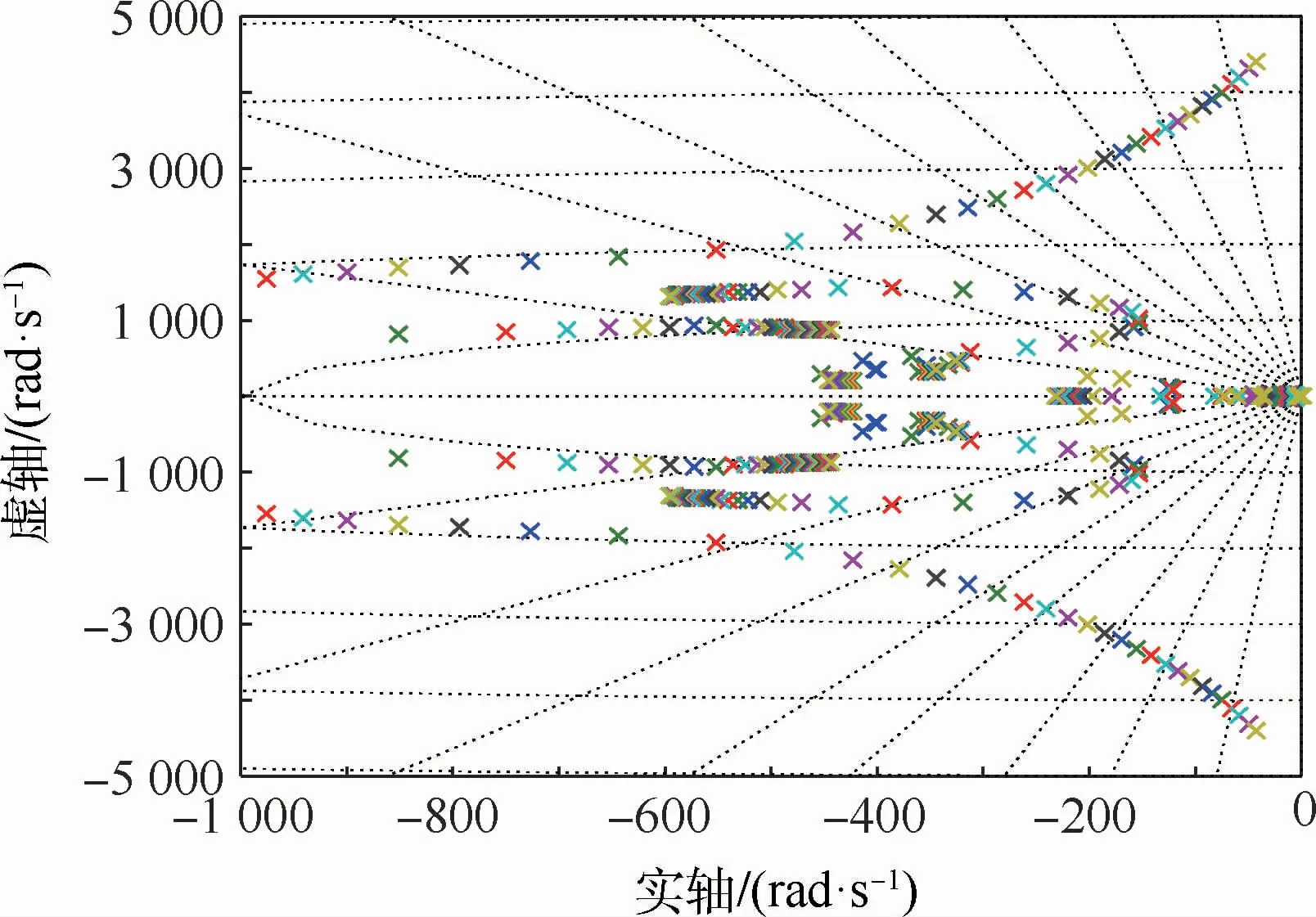
图6 复合控制下磁轴承系统根轨迹图Fig.6 Root locus of magnetic bearing system with composite control method

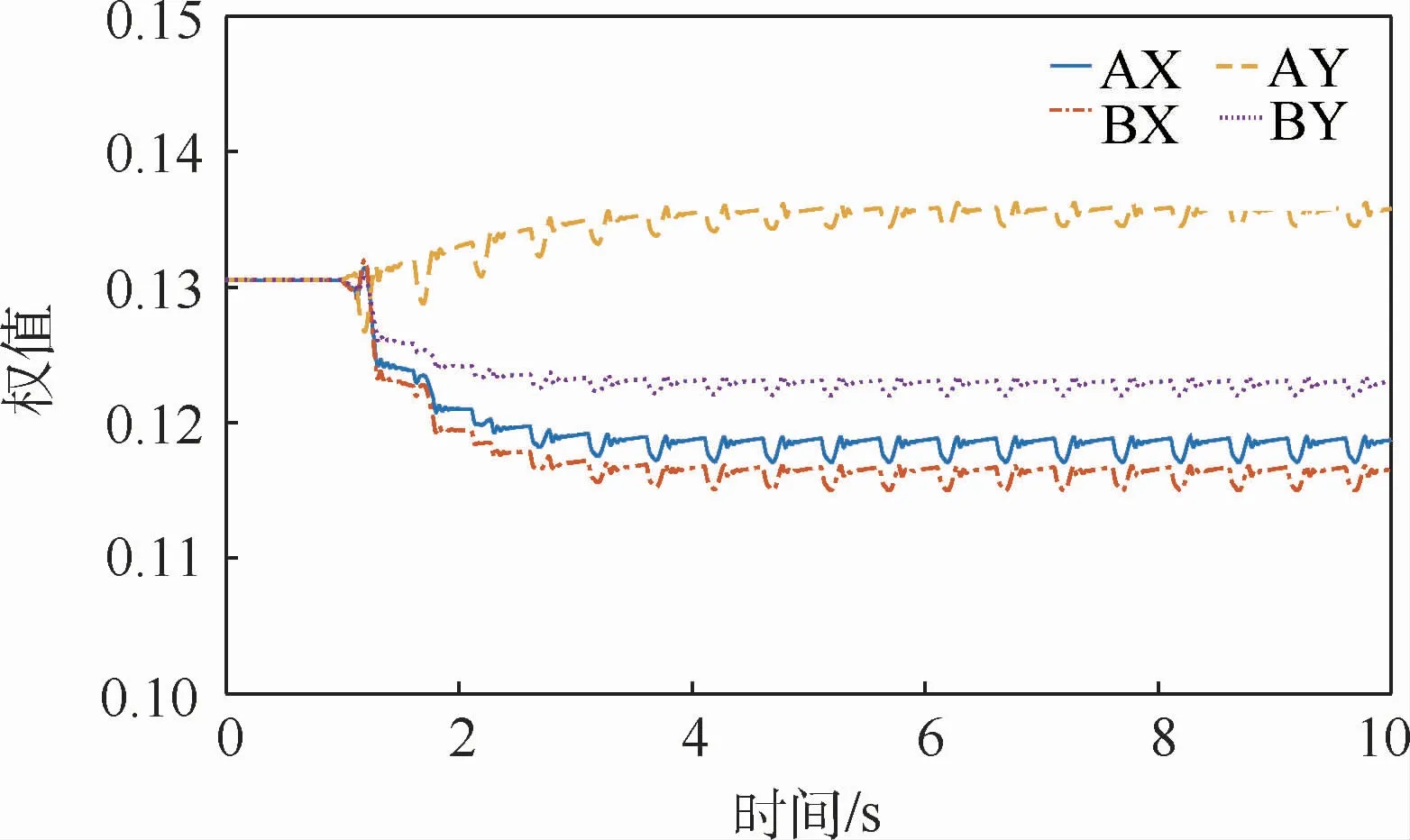
图7 角加速率自适应算法权值波形Fig.7 Weight value waveform of adaptive angular acceleration rate algorithm

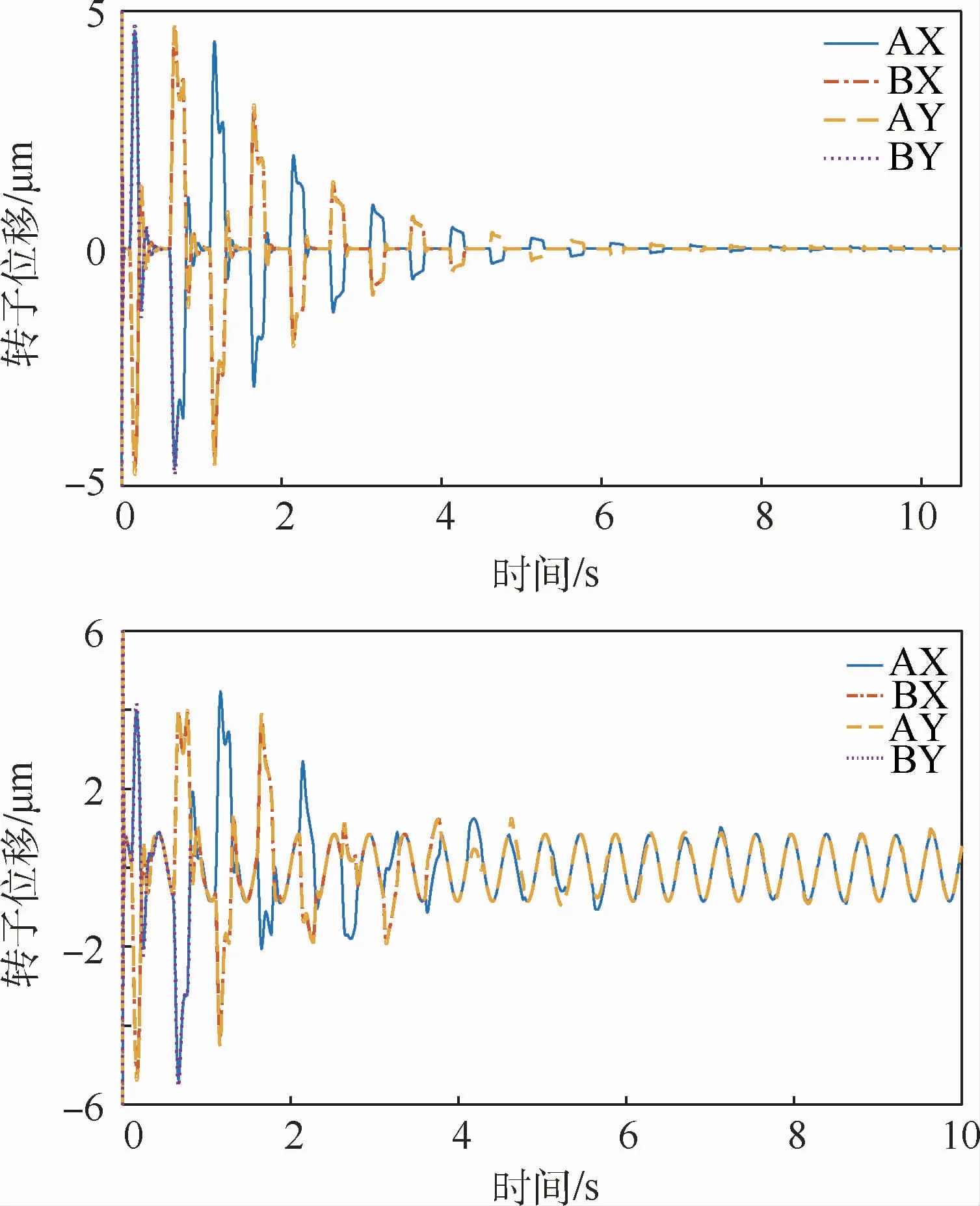
图8 基于复合控制的转子位移波形Fig.8 Rotor displacement waveform with composite control method

图8为基于复合控制的转子位移输出波形。将框架转动产生的26 N·m大小的扰动力矩接入磁轴承系统，转子的输出波形如图8（a）所示，转子位移峰峰值在t＝0 s时为4.81μm；在t＝2 s时收敛至2.07μm；在t＝6 s时收敛至0.13μm；在t＝10 s时收敛至0.048μm，之后峰值稳定不变，表明复合控制能显著补偿动框架效应。再向转子系统输入端的4个通道均接入一个幅值为20 N、频率为15 Hz的正弦波扰动信号，且接入AX、BY通道与AY、BY通道的扰动信号相位差为90°，转子输出波形如图8（b）所示：转子位移峰峰值在t＝1 s时最大，为4.65μm；在t＝2 s时收敛至2.79μm；t＝5 s时收敛至0.85μm，之后峰峰值基本不变，表明复合控制不仅能有效补偿动框架效应，对于未建模扰动也有明显的抑制作用。

4 实验验证

4.1 实验平台

为验证所设计的复合控制方法的有效性，以北京航空航天大学研制的MSCMG系统为对象进行实验研究。实验装置如图9所示，包括MSCMG样机、电源、控制器、示波器及监控系统等，样机额定角动量200 N·m·s，输出力矩50 N·m，转子转速Fr＝150 Hz，框架角速率由框架伺服电机控制部分直接给出，角加速率信号由角速率信号通过不完全微分得到。在此条件下，分别采用优化后PID控制方法、ADRC方法和本文提出的复合控制方法进行实验，比较3种控制方法下的转子位移跳动量、收敛时间、收敛后的位移峰峰值，校验该复合控制方法在磁轴承抗干扰能力上的优越性。MSCMG模型参数如表1所示，控制器参数如表2所示。

4.2 实验结果及分析

图10为基于PID控制的转子位移波形图。t＝0 s时高速转子开始旋转，陀螺框架未转动，由于不平衡振动的存在，转子输出位移持续跳动，最大跳动量为14.7μm；在t＝2 s时开始转动陀螺框架，在动框架效应的影响下转子位移跳动量加大为36.74μm；系统在t＝4 s之后收敛，收敛后的位移峰峰值为18.7μm。

图9 MSCMG实验平台Fig.9 Experimental setup of MSCMG

图11为基于ADRC的转子位移波形。在t＝1.5 s时开始转动陀螺框架，在t＝3.2 s之后系统收敛，收敛时间较传统PID控制减少0.3 s，收敛后的位移峰峰值为14.7μm，较传统控制下降21.4%。

表1 MSCMG模型参数Tab1e 1 Mode1parameters of MSCMG

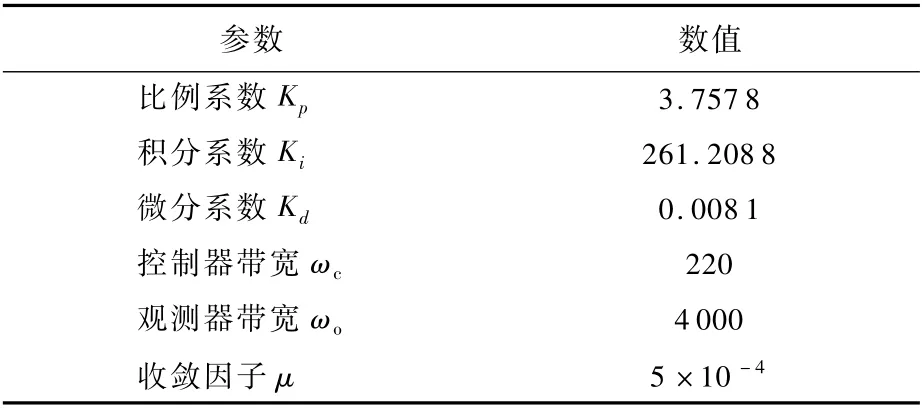
表2 磁轴承转子控制参数Tab1e 2 Contro1parameters of magnetic bearing rotor

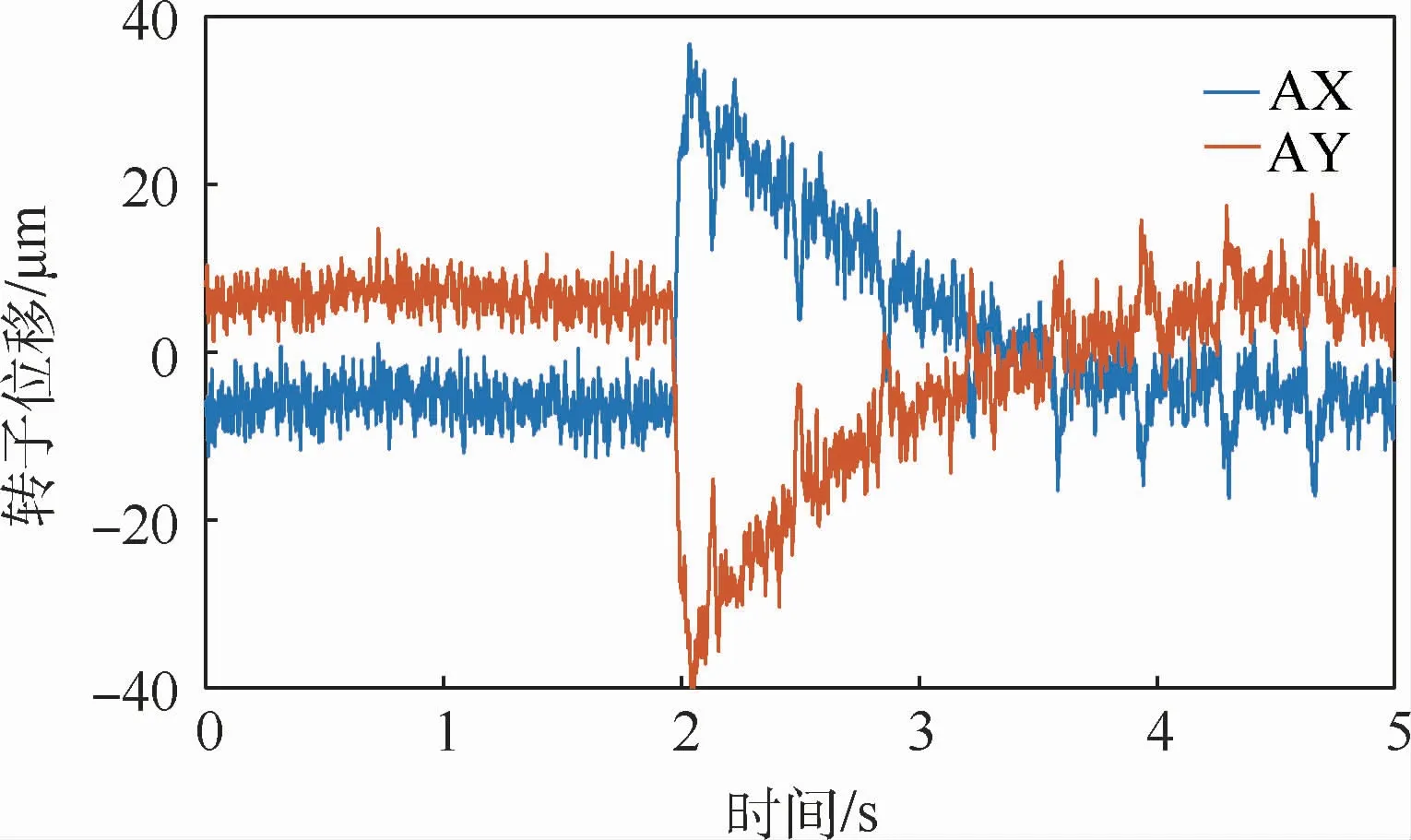
图10 基于PID控制的转子位移波形Fig.10 Rotor displacement waveform with PID control method

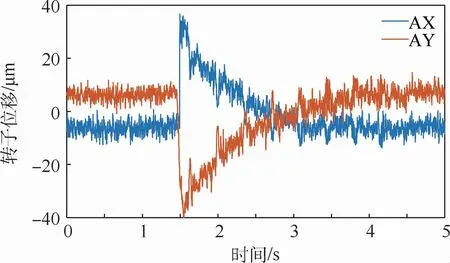
图11 基于ADRC控制下的转子位移波形Fig.11 Rotor displacement waveform with ADRC method

图12为复合控制下的转子位移波形。在t＝1.3 s时开始转动陀螺框架，系统在t＝2.2 s之后收敛，较传统控制提前1.1 s；收敛后的位移峰峰值为11.3μm，较传统控制下降39.6%。

综上分析可知，角加速率自适应前馈控制与ADRC复合控制方法明显改善了磁轴承系统特性，提高了系统精度，对扰动达到了理想的抑制效果。由于实验时框架角速率从－15°／s瞬间加至15°／s，角加速度过大，瞬态过程频率特性较为复杂，所以瞬态过程的控制效果不明显，有待于进一步深入研究。

图12 复合控制下的转子位移波形Fig.12 Rotor displacement waveform with composite control method

5 结 论

1）根据MSCMG动力学模型可知，动框架效应会影响高速转子的悬浮精度及稳定性。基于角加速率自适应前馈控制与ADRC相结合的复合控制方法，能够有效抑制框架转动对磁悬浮系统带来的影响。

2）ADRC控制器通过ESO对框架系统的未知扰动进行观测和估计，通过反馈控制实现对系统中未知扰动的补偿。

3）本文提出的复合控制方法改善了动框架效应及未知扰动对转子悬浮精度的影响，同时提高了磁悬浮系统的抗干扰能力，实现了MSCMG磁悬浮转子系统的高精度控制。