基于模糊PID的水下金刚石绳锯机张紧力控制策略研究

徐田丰杨 启

(1.上海交通大学 海洋工程国家重点实验室，上海200240；2.上海交通大学 高新船舶与深海开发装备协同创新中心，上海 200240；3.上海交通大学海洋水下工程科学研究院有限公司，上海200231)

0 引 言

近年来，海洋工程产业规模不断扩大，海洋油气资源的开发利用也迅速发展，为国家能源供给提供了重要保障。随着海洋油气田的不断开发与发展，很多使用年限较长的海底石油管道与导管架平台逐步被废弃，需要通过水下切割作业进行拆除。在各类切割方法中，水下金刚石绳锯机凭借环保清洁、对环境要求低等特点，成为国内外研究与发展的热点。上海交通大学针对胜利油田导管架平台拆除问题，研制了水下金刚石绳锯机样机，并开展了大量的切割试验研究[1]。除了废弃桩基的拆除，金刚石绳锯机还被应用于海底装备维修、打捞等海洋工程领域，2000年，在俄罗斯库尔斯克号核潜艇的打捞工作中，采用金刚石绳锯机完成了艇体外壳的分割作业[2]。

水下金刚石绳锯机是一种柔性切割工具，在切削过程中，切割平台在行进系统的推动下朝被切工件移动，通过金刚石切割链高速转动对工件进行磨削，完成切割作业。切割链张紧力与磨削力密切相关，过小的张紧力会使切削工件速度较慢，效率低下；而过大的张紧力则会加快金刚石串珠的磨损，甚至造成切割链绷断的风险。因此关于切削过程中切割链张紧力控制策略的研究对于提高切削效率具有重要意义。张永锐等通过金刚石绳锯切削海底管道效率试验得到串珠绳张紧力与切削压力的关系曲线[3]。王海波等进行金刚石绳锯切割管道的正交试验，对切割过程中串珠绳张紧力与其他切削参数进行了优化与协调[4]。Wu等针对金刚石线切割锯绳张力控制提出了一种PI(比例积分)控制方法[5]。

本文针对水下金刚石绳锯切削过程进行动力学建模，构建切割系统状态空间方程，进而提出一种基于模糊PID的切割链张力控制策略。通过仿真试验，验证了该策略的鲁棒性与动态性能。

1 水下金刚石绳锯切割动力学分析

1.1 切割系统动力学模型

常见的水下金刚石绳锯机本体结构如图1所示，主要由切割装置(包括切割链与切割滑轮)、行走装置、夹紧装置以及上下平台结构等部分组成。从事切割作业时，母船在预定海域将金刚石绳锯机下放到水中，经由潜水员的辅助将夹紧装置固定在海底石油管道、导管架平台等目标上。母船通过脐带缆等装置与绳锯机相连，进而控制切割过程。

水下金刚石绳锯切割系统的简化动力学模型如图2所示，其中，轮1与轮2为可调整从动轮，轮3与轮4为主动切割轮，主动切割轮参数相同，可输出同样大小的驱动力矩。

考虑到工程实际情况，在建立水下金刚石绳锯切割动力学模型之前，对其做出以下假设：

图1 水下金刚石绳锯机本体结构

(1) 将金刚石切割链整体看作是具有一定刚度的弹簧。

(2) 在切割过程中，金刚石切割链和滑轮不发生相对运动，受到的阻力与阻力矩均作用在滑轮上。

图2 水下金刚石绳锯切割系统动力学模型

在上述假设的基础上，水下金刚石绳锯切割系统的动力学方程为

式中：R=262.5 mm，为切割滑轮的半径；T1～T5分别表示各个滑轮两侧金刚石绳链的张紧力；M3与M4为主动轮3和轮4提供的驱动力矩，大小相等；Md1～Md4分别为4个滑轮在切割过程中受到的阻力矩，其中包括由于滑轮与锯绳之间摩擦作用而产生的阻力矩。当绳锯机在水下从事切割作业时，滑轮受到的海水黏滞力矩为阻力矩的主要组成部分，根据流体力学相关理论，海水黏滞力矩的大小[6-7]：

式中：γ=1 023 kg/m3，为海水的密度；ν=1.01×10-6m2/s，为海水的运动黏性系数；ω为滑轮转动的角速度。

1.2 金刚石切割链张紧力分析

水下金刚石绳锯通过驱动行进系统实现对工件的切割，当切割系统的进给速度与磨削工件的速度匹配时，切削压力与锯绳张紧力达到较为平衡的状态，此时串珠与金刚石磨粒处于正常磨损状态。增大行进系统前进油缸的压力，使切割系统的进给速度超过磨削工件的速度，锯绳会进一步张紧，进而增大磨削力，提升切削效率。但张紧力与磨削压力过大时，一方面会加剧金刚石串珠与磨粒的磨损，另一方面，锯绳也会有绷断的风险。图3所示为通过绳锯切割试验测得的锯绳张紧力与其变形伸长挠度之间的关系，从图中可以看出，在一定范围内，锯绳的张紧力与其进给运动产生的挠度成近似线性关系，即

式中：T0为锯绳的初始张紧力；y为锯绳伸长的挠度；K1为锯绳的刚度。图3所示的关系也与上文所说的假设(1)相符。

图3 锯绳张紧力随挠度变化曲线

当量磨削厚度常被人们用来描述磨削过程[8]，根据Bus等的研究，当量磨削厚度与磨削工件所受的磨削力在一定范围内具有良好的线性关系[9]。对于金刚石绳锯切割，在磨削过程中，工件由夹紧装置夹持，保持固定，因而其当量磨削厚度可视作金刚石串珠绳的磨削厚度。设h为切削时金刚石串珠的磨削厚度，Ft为主切削力，上述关系可以表示为

设串珠的宽度为b，则其沿切向的切削面积为

设锯绳上相邻两串珠的间距为L，Vs为切割链转动的线速度，则在单位时间内，绳锯切除工件的厚度，即绳锯切削工件的速度为

结合式(3)，若切割系统的进给速度为Vk，则在一小段时间dt内，锯绳张紧力的变化：

变化率为

1.3 金刚石串珠切割过程力学分析

在金刚石绳锯切割工件的过程中，单个串珠受力状态如图4所示，其两端锯绳拉力分别记为Ti与Ti+1，设单个串珠引起的锯绳张紧力变化为dT，即Ti+1=Ti+dT。串珠受到工件的法向作用力Fn，用以磨削的切向作用力Ft。绳锯在切割海底石油管道等工件时，以一定的弧度依附于工件表面，设单个串珠在工件上的包角为dα，则锯绳张紧力与串珠运动方向夹角为在切割过程中，单个串珠尺寸相对于工件来说很小，则有

根据以上分析，串珠切向受力平衡方程为

法向受力平衡方程为

以上两式整理后，可得

进一步可得

对式(7)左右两边进行积分，便可得到串珠两侧锯绳张紧力之间的关系，即

图4 单个串珠切削过程受力分析

1.4 切割系统状态空间

综合上文给出的切割系统动力学方程式(1)以及式(8)、式(14)，金刚石绳锯切割系统的状态空间方程如下：

式中：x(t)=T1(t)，为切割系统从动轮处锯绳张紧力；u(t)为切割系统的进给速度，即系统的输入；y(t)为系统的输出；K1(t)为锯绳刚度系数；K2(t)是与绳锯切割线速度、串珠自身形状、工件材料特性等因素有关的参数；Fd(t)为系统的干扰，一方面来源于主动轮驱动力矩，海水黏滞力矩等，另一方面来源于信号干扰与测量误差。从上面的状态空间方程可以看出，切割系统是一个具有多参数的时变系统，随着切割的进行，系统部分参数将会发生改变，造成系统的扰动。

2 模糊PID控制模型

在金刚石绳锯切割过程中，切割链张紧力的大小与多种切削参数相关。本文考虑工程的实际情况，假设绳锯机在切割过程中，主动切割轮转速稳定，金刚石切割链保持一定的线速度，此时切割系统的进给速度是影响切割链张紧力的主要因素。为避免切割链张紧力剧烈波动造成切割效率下降以及锯绳断裂，本文采用模糊PID控制策略对切割链张紧力进行控制。相比于传统的PID控制策略，模糊PID控制根据传感器反馈的张紧力的误差与误差变化率，通过模糊推理对切削状态进行判断与分类，再根据知识库中的模糊规则选取合适的输出，实时调整PID控制器的参数，使张紧力处于稳定的状态。

模糊PID控制模型如图5所示，控制器以切割链预设张紧力T(t)与实际张紧力T'(t)的误差值e(t)以及误差值的变化率de(t)/dt作为输入，经过模糊推理环节后输出PID控制器参数Kp、Ki、Kd的补偿值ΔKp、ΔKi、ΔKd，从而调节PID控制器参数。对于PID控制器，其输出为切割系统进给速度的控制量Vk(t)，控制方程为

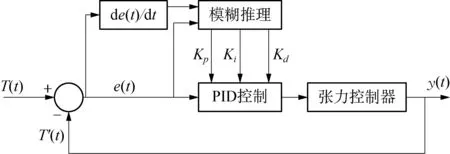
图5 模糊PID控制模型

3 模糊PID控制仿真

3.1 恒张紧力仿真

为检验本文模糊PID控制方法对切割链张紧力的控制效果，采用仿真软件进行相应仿真实验分析，并将结果与传统PID控制进行对比。模糊PID控制器的初始参数Kp、Ki、Kd与传统PID控制器相同。控制系统的目标张紧力，根据相关试验与金刚石切割链性能指标设为220 N，仿真总时间为200 s，采样周期Ts=0.1 s。

切割系统状态空间方程由式(15)给出，式中，锯绳刚度系数K1=2 621 N/m，由试验测得，在仿真过程中视为常数。系统状态空间方程系数K2与线速度、串珠形状、材料特性等因素有关，具有一定的时变性。为检验控制系统的鲁棒性，引入系统参数的摄动，在t=100 s时将参数K2突然增大至原先的2倍。对于干扰项Fd，其来源于驱动力矩与阻力矩的部分，在仿真中保持不变；由于信号与测量误差造成的系统干扰具有随机性，因此在仿真过程中简化为高斯白噪声。

需要注意的是，在工程实践中，切割系统的进给速度存在额定值与最小值，为了使仿真结果与实际情况更相符，在控制系统中加入筛选环节，使切割系统进给速度的控制量维持在其限定范围内。

模糊PID控制与传统PID控制的仿真结果如图6所示，从图中可以看出，模糊PID控制的超调量与调整时间均小于传统PID控制。当系统的参数发生突变时，模糊PID控制系统受到的影响较小，张紧力可以在很短的时间内收敛到目标值，而传统PID控制系统则会产生一定量的偏差，50～60 s后收敛到原设定值。以上结果表明，模糊PID控制具有较强的鲁棒性。

图6 系统参数突变时的仿真结果

3.2 动态性能仿真

水下金刚石绳锯在实际切削过程中，由于磨削力的限制，其磨削工件的速度相对较小，因而在工程实践中，金刚石绳锯磨削工件通常采用步进式的方案，即在短时间内给行进系统一个较大的进给速度，使整个切割框架向前移动一小段距离。此时，锯绳张紧力以及磨削力增大，绳锯切削工件速度加快。随着切削过程的进行，绳锯的变形伸长逐渐恢复，张紧力不断减小，直至达到平衡状态。通过循环往复这一过程，实现对工件的切割。根据上文的描述，切割链张紧力在切削过程中表现为锯齿状的变化。为检验本文中模糊PID控制系统的动态性能，设置锯齿力为系统输入：

式中：INT()为取整函数，锯齿力的峰值与谷值分别为250 N与200 N，周期为50 s。为进一步检测控制系统的动态性能，相比于上述过程中张紧力的瞬时增长，考虑张紧力在每个步进周期内缓慢增长的情形，设置正弦力作为系统输入，同样进行仿真试验：

其中，正弦力的峰值与谷值分别为250 N与200 N，周期为100 s。

两种目标张紧力及各自不同控制方式的仿真实验结果如图7与图8所示。

图7 锯齿力控制仿真结果

图8 正弦力控制仿真结果

表1为模糊PID控制与传统PID控制的性能指标的对比，结合表1与上文控制结果曲线，可以看出模糊PID控制相对于传统PID控制具有响应速度快、平均误差小以及波动较小的特点。对于锯齿型目标张紧力，模糊PID的平均误差为传统PID的51%，标准差为传统PID的66%；对于正弦目标张紧力，模糊PID控制的平均误差为传统PID的69%，标准差为传统PID的90%。以上结果表明，本文采用的模糊PID控制系统对于动态控制目标具有较好的控制效果和性能，可以有效提高控制精度。

表1 两种方式控制性能对比

4 结 语

本文首先从整体上建立了金刚石绳锯切割系统的动力学模型，之后从总体到局部，对切削过程中锯绳自身以及单个串珠进行了力学分析，将以上各个力学方程串联，构建了以切割系统进给速度为输入，切割链张紧力为输出的切割系统状态空间方程。

在切割系统状态空间方程的基础上，提出了一种基于模糊PID的切割链张紧力控制策略。进行恒张力控制仿真实验，在仿真中引入系统参数的摄动。结果表明，模糊PID控制策略相较于传统PID控制具有更强的鲁棒性。同时进行动态张紧力控制仿真实验，仿真结果显示模糊PID控制的动态性能优于传统PID控制，能够有效减小切削过程中切割链张紧力的波动，提高控制精度。

水下金刚石绳锯机张紧力受多种切削参数影响，本文以进给速度为控制量，提出的模糊PID控制策略对于工程实践中切割链张紧力的控制以及切削效率的提升具有参考意义。