非线性管土模型在海底管道悬跨疲劳评估中的应用
王 猛
(海洋石油工程股份有限公司,天津 300451)
0 引 言
在海底管道自由悬跨分析中,管土作用对悬跨静态平衡和动态响应有重要影响。在静态分析中,应考虑沿管道的海床轮廓。例如,对于斜度较大的海床,静力平衡中需要考虑土壤轴向摩擦力。在动态分析中,土壤约束条件影响管道的自然频率,而管土接触力作为阻尼力直接影响管道的动力响应。如果考虑非线性接触力,则必须在动态分析中考虑土壤刚度和阻尼的短期和长期特性。
近年来,学者们对管土接触模型展开了深入研究。Bridge等[1]分析和总结了STRIDE和CARISIMA[2]两个国际工业联合研究项目取得的实验数据和成果,提出了土壤支撑力与吸力的循环模型。Aubeny等[3-4]在Bridge等的模型基础上, 相继提出了非衰减和衰减刚度的管土模型。Nakhaee等[5-6]根据Aubeny等提出的管沟底部海床刚度具有衰减效应的模型,并改进了程序CABLE3D。You[7]讨论了海床与钢悬链立管作用的数值模型,提出了简化的弹簧支撑模型。基于Bridge和Aubeny的管土模型,Randolph等[8]提出了新的模型数学表达式。
本文将非线性管土作用模型应用于海底管道悬跨评估,分析该模型对管道悬跨疲劳的影响。
1 土壤模型
1.1 非线性模型
Randolph等[8]基于Bridge[1]和Aubeny[2]的管土模型,提出了新的管土模型的数学表达式。管土相互作用的P-y曲线如图1所示。土壤的极限支撑力和极限吸附力作为土壤力的包络线。根据实验数据和有限元分析结果,使用幂指数函数拟合得到较好的结果。

图1 典型的土壤P-y曲线

式中:Nc为支撑力系数,当z/D>0.1时,Nc=a(z/D)b;当z/D<0.1时,Nc=a(0.1)b(10z/D)0.5;a和b为拟合系数;Su(z)为土壤剪切强度,随沉降深度线性变化;D为管道外径。式(2)中,fsuc为吸附力系数。
在管道沉降阶段,Bridge和Aubeny提出的模型中的支撑力按包络线考虑。Randolph引入了双曲线进行修正,土壤支撑力减小为ζ/(1+ζ)倍。

在A点,管道停止沉降开始向上运动,土壤支撑力减小,在B点减小至0。整个B—D阶段,管道受到土壤吸附力。土壤吸附力分为两个阶段:B—C阶段,吸附力逐渐增大,在C点达到极值;C—D阶段,吸附力逐渐减小,在D点减小至0,表明管土分离。Randolph的模型将管道上升时土壤作用力分为两个阶段:A—C阶段按式(4)计算,C—D阶段按式(5)计算。

对式(4)变换,可以得到P(z)=P0+该曲线形式与Aubeny模型中A—C阶段曲线相同。在C—D阶段,Aubeny的模型采用三次曲线拟合。Randolph将此阶段表达为吸附力包络线的指数衰减。这是因为实验发现,吸附力只能在管道上升的一定位移时存在[1]。当管道上升位移大于一定值时,吸附力开始衰减。即图1中C点后吸附力衰减,吸附力应按式(5)计算。
当管道抬升至某位置停止抬升时,进入再沉降阶段,再沉降起点可能位于管道上升过程中的任一位置,即A—D曲线段中的任一点。土壤在管道循环升沉载荷的作用下,被不断扰动,刚度发生衰减。立管下部流场的变化对土壤管沟的冲刷作用也导致土壤刚度减小[3]。土壤刚度减小可考虑为P-y曲线回弹至A点的位移时,支撑力只恢复到F点位置。
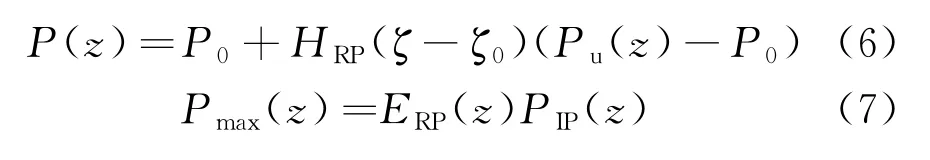
1.2 线性模型
作为比较,使用线性管土作用模型进行悬跨评估。简化的线性土壤刚度按DNV GL-RP-F114给出的方法计算。
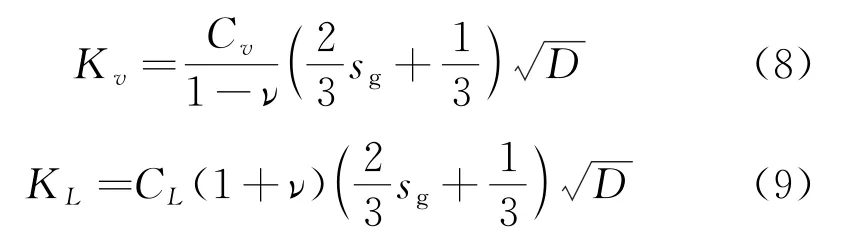
式中:Cv为土壤垂向刚度系数;CL为土壤侧向刚度系数;sg为管道重与浮力比;D为管道外径。
2 悬跨疲劳分析
2.1 有限元模型
本文使用Orcaflex软件对海底管道悬跨进行疲劳评估。管道外径为219.1 mm,壁厚为12.7 mm,为消除边界条件效应,模拟管道总长度为100 m,其中悬跨段长度为20 m,跨高为0.5 m,如图2所示。

图2 悬跨模型
水深为100 m。为简化计算,不考虑流。设计寿命按20年考虑。百年重现期有义波高为13.13 m,谱峰周期为16.24 s。按Longuet-Higgins[9]方法将波谱离散为规则波。规则波覆盖概率为0.909,共105个工况。
S-N曲线取DNV GL-RP-C203[10]
D曲线。疲劳曲线公式如下:
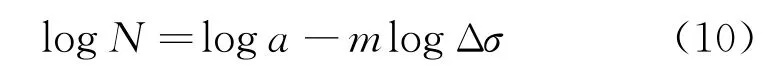
式中:
N为应力幅值对应循环次数;a、m为与材料疲劳特性相关的参数;Δσ为应力幅值。对于D曲线,当N≤106时,m=3, loga=11.764;当N>106时,m=5,loga=15.606。
土壤参数如表1所示。

表1 土壤参数
2.2 分析结果
2.2.1 模态分析
对线性土壤和非线性土壤的悬跨进行模态分析,取四阶模态,结果如表2所示。线性刚度土壤的悬跨自然频率约为非线性刚度土壤的悬跨自然频率的1.22倍。
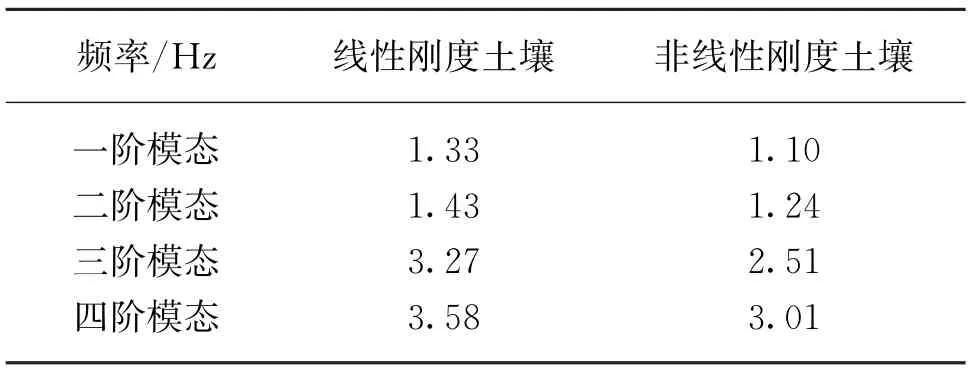
表2 悬跨自然频率
2.2.2 应力分析
对两种土壤模型的悬跨进行动态分析。悬跨段管道相当应力如图3所示。在跨肩位置,线性土壤的悬跨应力大于非线性土壤;而在无土壤接触管段,线性土壤的悬跨应力小于非线性土壤的悬跨应力。
作为比较,采用以上管道和环境参数,按DNV GL-RP-F105[11]规范计算的von Mises应力为40.1 MPa。

图3 悬跨相当应力
2.2.3 疲劳寿命
使用线性土壤模型和非线性土壤模型计算的悬跨疲劳寿命如图4所示。计算的悬跨最小疲劳寿命分别为27.77年和25.59年,发生位置分别在跨中50 m和跨肩38.5 m处。作为比较,采用以上管道和环境参数,按DNV GL-RP-F105规范计算的最小悬跨寿命为24.08年。

图4 悬跨疲劳寿命
在跨肩位置,非线性土壤的管道疲劳寿命大于线性土壤的管道疲劳寿命。在跨中位置,非线性土壤的管道疲劳寿命小于线性土壤的管道疲劳寿命。
对于整个悬跨的最低疲劳寿命,非线性土壤模型出现在跨中,为25.59年;而线性土壤模型出现在跨肩,为27.77年。
3 关键参数敏感性分析
非线性土壤模型中的关键参数包括幂指数系数a和b,无量纲土壤最大刚度Kmax,吸附力系数fsuc,附力衰减系数λsuc,再沉降系数λrep。Randolph等[8]给出的建议值如表3所示。

表3 土壤模型关键参数
关键参数控制土壤模型的各个阶段的土壤接触刚度的变化。但对悬跨疲劳的影响,需要进行分析才能进一步确定。将基础工况作为工况1,考虑单参数变化的敏感性分析工况如表4所示。

表4 敏感性分析工况
在左侧跨肩38.5 m位置,各工况土壤接触力与规则化沉降关系曲线如图5所示。各工况悬跨疲劳寿命计算结果如图6所示。工况2的悬跨最小疲劳寿命发生在跨肩位置,为27.42年;其余工况的最小疲劳寿命的位置出现在跨中,其中,工况3的疲劳寿命最小,为25.39年。
土壤接触力对土壤剪切刚度Su和吸附力fsuc比较敏感。当剪切强度增大时,土壤接触力增大,管道沉降量减小,管土P-y曲线在较窄范围内变化。与线性模型类似,较硬的土壤导致跨肩疲劳损伤增大,整个悬跨的最大损伤出现在跨肩位置。这说明在管土模型各参数中,土壤刚度仍然是影响管道疲劳损伤的最主要因素。

图5 跨肩位置土壤接触力与规则化沉降关系曲线
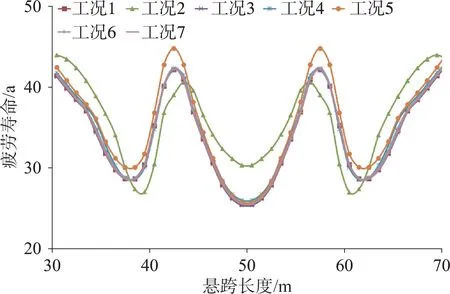
图6 悬跨疲劳寿命敏感性分析
在土壤表层土剪切强度相同的情况下,吸附力比fsuc大时,管道抬升过程中受到的吸附力增大,且管道沉降量也有明显增大,沉降范围为0.08D~0.16D。在循环载荷作用下,土壤呈现软化趋势,使跨肩处管道疲劳损伤减小,损伤的最大处出现在了跨中。
4 结 语
本文将非线性接触刚度模型应用于海底管道悬跨评估,分析结果与采用线性刚度模型和按DNV GL-RP-F105方法计算的结果进行了对比。通过敏感性分析,确定了模型中关键参数对悬跨疲劳的影响。得到如下结论:
(1) 关键参数中的土壤接触力对土壤剪切刚度Su和吸附力比fsuc较敏感,而对无量纲化最大刚度Kmax、吸附力衰减长度λsuc和再沉降偏移系数λrep不敏感。
(2) 土壤剪切强度较大时,管道沉降量较小,P-y曲线变化范围较窄。
(3)非线性土壤在循环载荷作用下发生软化,使跨肩处管道疲劳损伤减小,损伤的最大处出现在了跨中。
非线性土壤模型更接近实际土壤行为。对于浅水海底管道工程,一般不选择疲劳作为设计准则,使用线性土壤模型可以得到满意的分析结果。对于深水管道,疲劳分析是管道设计的主要工作。精确的土壤模型可以获得更准确的疲劳分析结果。需要注意的是,由于土壤参数的不确定性,需要依据土壤详细的评估结果和工程经验谨慎选取非线性模型相关参数。

