电网在线等值新方法

甘 明

同济大学 电子与信息工程学院 上海 201804

1 研究背景

准确且完备的网络参数是电力系统状态分析、调度、优化的前提,是电网一体化运行的基础[1-2]。随着电力系统互联的不断深入,互联电网间的影响日益增强。在这样的背景下,各电力运营主体间受信息保密性或经济利益等方面影响,往往不愿意公开完全、准确的信息[3]。另一方面,相邻电网传递来的信息也存在与本管辖网络内信息采集时刻一致性问题,对系统分析及控制的有效性带来一定影响,甚至会出现潮流计算不收敛等问题,给管辖电网的运行安全性、稳定性带来风险[4-5]。面对以上情况,在没有任何外网信息的条件下,如何给出比较准确的外网等值网络,并以此完成本网络准确的分析及控制,成为备受关注的研究课题。

目前,外网信息未知的黑箱外网等值方法基本基于内部系统的测量数据,采取各种策略估计出外部网络等值参数。文献[5-6]提出单端口戴维南等值方法,采用一个电压源串联一个阻抗来等值外部网络,通过建立边界节点处的多时段测量方程来求解等值参数。但是这一方法只适用于单端口网络的等值,且存在相邻测量时段测量值变化不大而导致参数估计不收敛的问题。文献[7-8]提出基于简化Ward等值方法,仅考虑边界节点的等值线路与等值注入功率,通过多次内网支路开合操作获得潮流状态数据,采用最小二乘法估计简化Ward等值参数。但是这一方法较难应用于在线等值,因为在实际运行时对内部网络进行非计划频繁开关操作往往是不允许的。文献[9]提出一种基于实测信息的两端口静态等值方法,这一方法不需要进行内网开断操作,但是仅适用于内外部网络间只含两个边界节点的网络。文献[10]提出一种两阶段多端口静态等值方法,首先估计简化Ward等值模型参数,然后估计扩展Ward等值模型参数。这一方法采用分步求解策略,降低了第二阶段各等值参数之间的耦合,在一定程度上提高了等值准确性。文献[9-10]本质上都是基于多时段测量方程来实现等值参数的最小二乘估计,当网络不发生较大变化时,同样具有等值参数估计不收敛及不稳定的问题。

在以上研究的基础上,笔者提出一种基于补偿法,由节点功率扰动获取补充测量信息,进行外网在线等值的新方法[11]。这一方法的等值网络包括边界节点间的耦合支路,以及外网与每一边界节点的等值阻抗与电源,可有效反映外网对内网的影响。这一方法不需要开断内网支路,以基于补偿法的节点功率扰动获取补充测量数据,解决当测量数据差异小、迭代矩阵条件数多时,等值参数估计迭代收敛困难、等值参数求解不稳定等问题。通过IEEE 39节点系统仿真算例证明了这一方法的有效性。

2 基于测量信息的在线等值网络与模型

2.1 在线等值网络

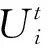
2.2 等值网络求解优化模型

对于图1所示在线等值网络,其边界节点的功率及电压在等值前后必须一致,即:

(1)

(2)

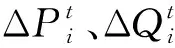
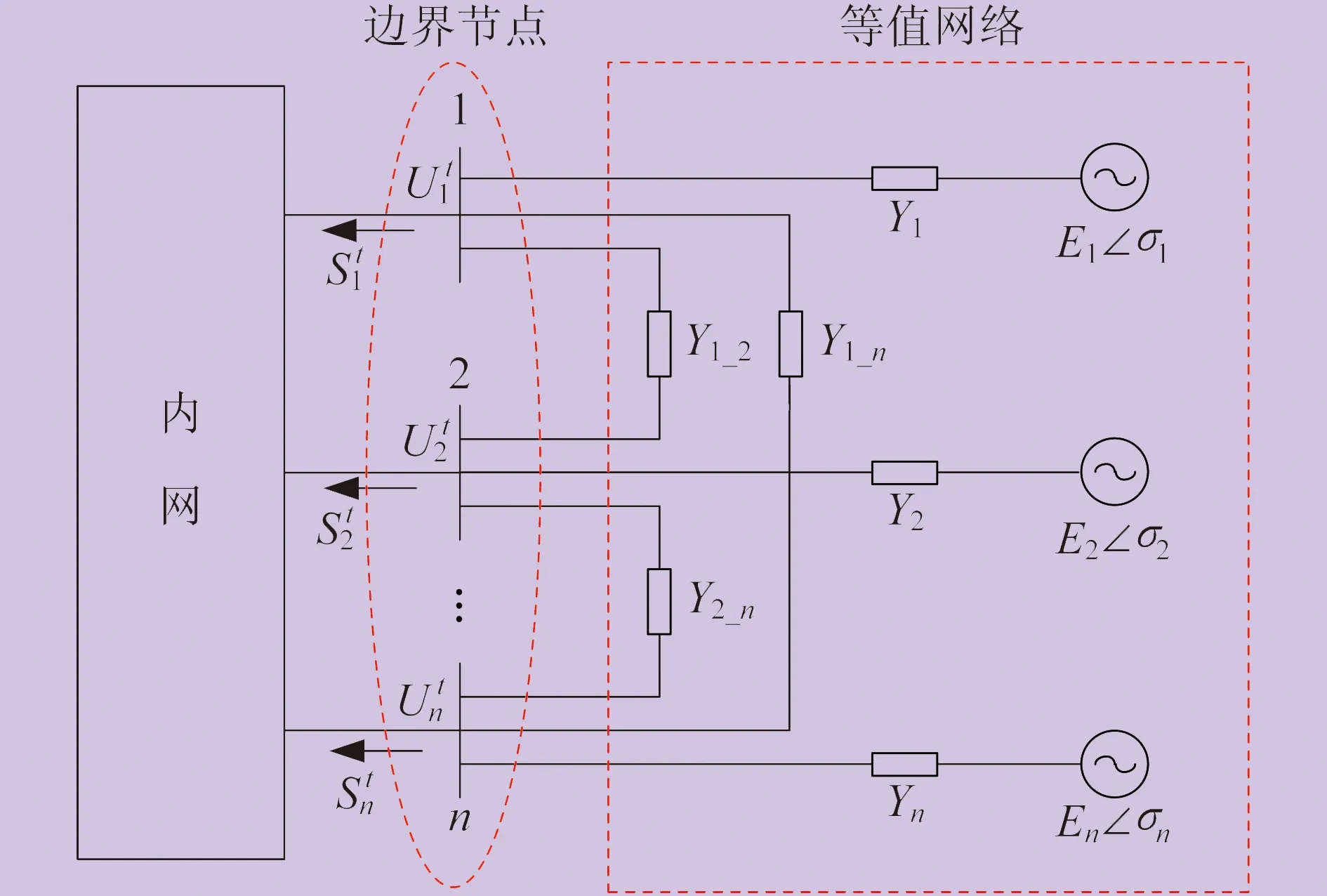
图1 基于内网测量信息的在线等值网络

(3)

(4)

(5)

(6)

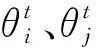
式(3)、式(4)中,待估计变量包括Ei、σi、Gi、Bi、Gi_j、Bi_j。

基于内部网络多个时间断面的测量数据,构建以边界节点等值网络计算值与测量值之差,即失配量二次方和最小为优化目标的最小二乘估计模型:

(7)

当边界节点数量为n时,待估计变量Ei、σi、Gi、Bi各有n个,Gi_j、Bi_j各有n(n-1)/2个,因此,待估计参数总数为n2+3n。每一测量时段可用测量方程有2n个,m个测量时段共有2mn个测量方程。为使式(7)可解,需满足测量方程数大于待估计变量数,即:

2mn≥n2+3n

(8)

根据式(8)可以确定所需测量时段数m。

3 基于补偿法的节点功率扰动

基于内部网络多时段测量信息的等值网络参数模型求解,本质上是假设在测量信息采集时间不长的前提下,外部网络状态不发生大的变化,仅内部网络状态发生变化,然后利用边界测量信息计算得到外网等值网络参数。在时间间隔不长的一段时间内,外部网络确实不会发生大的变化,但内部网络也可能不发生大的变化,此时边界测量值在相近的几个时段差别不大。对于这种情况,因为迭代线性方程组的因数矩阵条件数很高,所以迭代的收敛性很差或不收敛,即使收敛,计算得到的等值参数也不准确。研究表明,不同测量时段之间测量值变化百分比均值小于0.01%[12],等值参数估计就会非常不稳定,或出现不收敛问题。

为了克服这一问题,笔者提出基于补偿法的节点功率扰动,来模拟开断内网支路,进而获得有效的测量数据,避免内网支路实际开合操作影响网络安全运行。

假设支路a-b为模拟开断的支路,如图2所示。α为连接到节点a的母线集合,β为连接到节点b的母线集合,Paα+jQaα、Pbβ+jQbβ分别为节点a和b流入对应母线集合α和β的功率,Pa+jQa、Pb+jQb分别为节点a和b的注入功率,Pab、Qab分别为支路a至支路b模拟开断前的有功和无功功率,Pba、Qba分别为支路b至支路a模拟开断前的有功和无功功率,Pab=-Pba,Qab=-Qba。根据补偿法原理,模拟开断a-b支路,需在支路两端节点a和b处分别注入ΔPa+jΔQa和ΔPb+jΔQb功率扰动,在网络接近线性的条件下,注入功率满足:

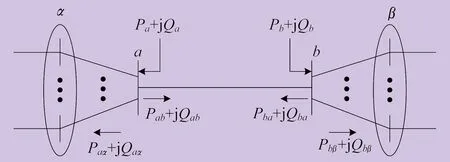
图2 内网a-b支路

(9)

偏导数方阵H为[11]:

(10)

在节点a和b注入功率扰动增量后,内网测量数据会有比较明显的变化,此时内网结构参数不变。将功率扰动后的内网测量数据代替功率扰动前的测量数据,参与式(7)求解,能够有效提高参数估计的收敛性。

利用内部网络测量信息及功率扰动后补充测量信息进行等值网络参数估计的过程如下:

(1) 根据边界节点总数,综合考虑等值参数的可估计性和估计精度,以式(8)确定内网测量数据时段数;

(2) 采集初始时段内网测量数据;

(3) 判断采集测量数据时段数能否满足等值参数估计需求,若满足要求,则进行步骤(5),否则采集下一时段测量数据,并与已采集测量数据进行比较;若与任意时段相比测量值变化百分比均值小于0.01%,则进行步骤(4),否则继续进行步骤(3);

(4) 选择不与边界节点相连的内网特定支路,在支路两端节点注入功率扰动,功率扰动大小通过式(9)确定,采集功率扰动后内网测量数据,返回步骤(3);

(5) 初始化在线等值网络等值参数Ei、σi初始值为1p.u.和0,线路参数Gi、Gi_j初始值为0.03p.u.,线路参数Bi、Bi_j初始值为0.3p.u.;

(6) 按式(7)构建的等值网络参数最小二乘估计模型求解等值网络的参数。

在线等值网络参数求解程序框图如图3所示。

4 算例分析

笔者以IEEE 39节点系统为算例,验证所提出方法的有效性。所有参数及计算结果均以标幺值形式表示。

假设电网结构不变,各负荷节点功率按典型运行方式下功率的0.01%步长递增,各发电机有功功率按典型运行方式下功率的0.01%步长递增,由此可以获得若干个时段的潮流解,用于模拟在线测量信息。

IEEE 39节点系统中以节点1、节点3和节点17为边界节点,以节点2、节点25～节点30、节点37～节点39为外网节点,其余节点为内网节点,如图4所示。系统有三个边界节点,根据式(8),需要三个时段的内网测量值,作为等值网络参数估计的测量信息。为充分模拟电力系统实际运行情况,验证不同情况下等值网络参数估计的收敛性,设计两种IEEE 39节点系统潮流解方案作为测量数据。方案一以典型运行方式潮流解为基准状态,即第一时段测量数据,以基准状态一次步长递增后的潮流解作为第二时段测量数据,以基准状态三次步长递增后的潮流解作为第三时段测量数据。方案二以典型运行方式潮流解为基准状态,即第一时段测量数据,以基准状态两次步长递增后的潮流解作为第二时段测量数据,以基准状态四次步长递增后的潮流解作为第三时段测量数据。

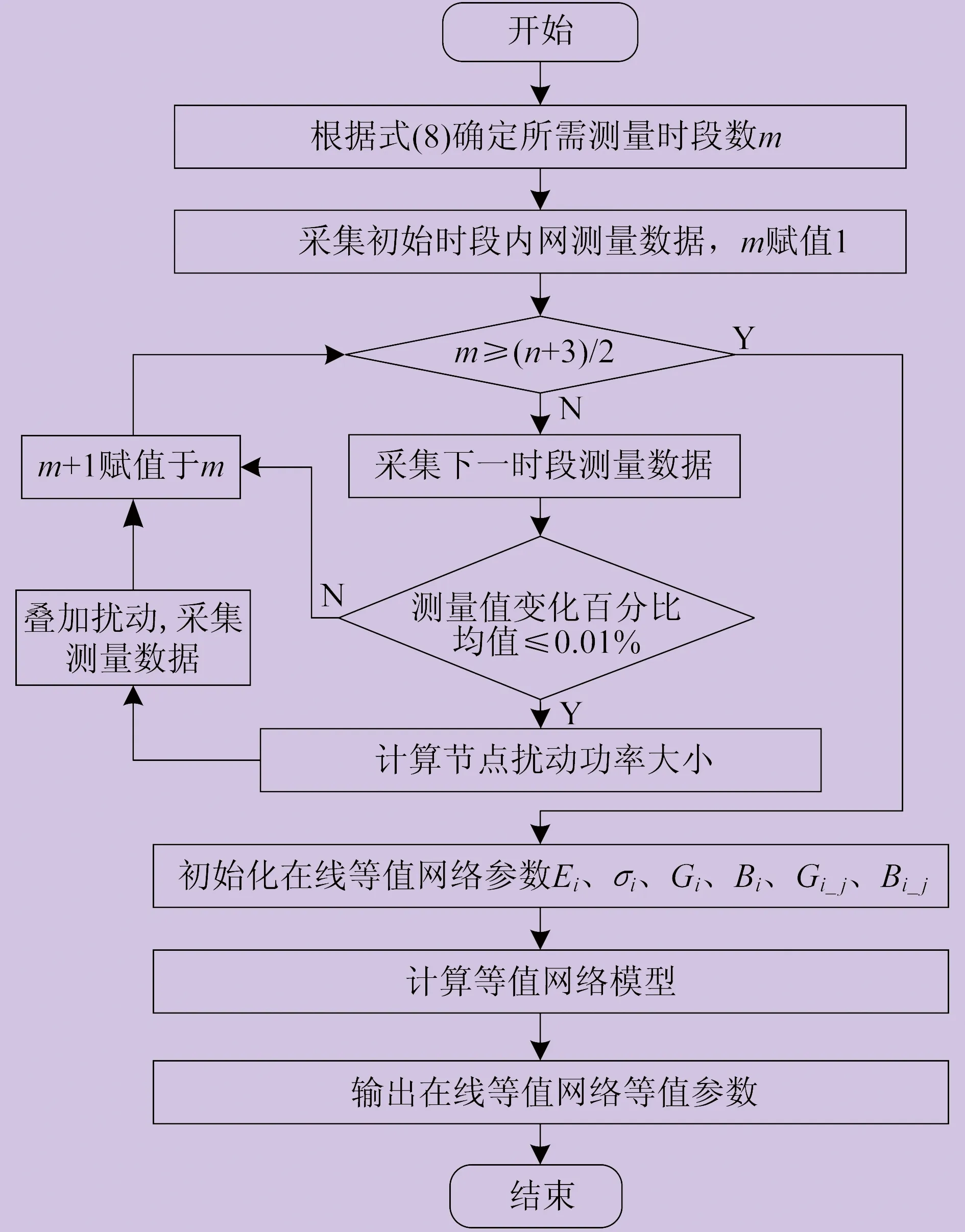
图3 在线等值网络参数求解程序框图

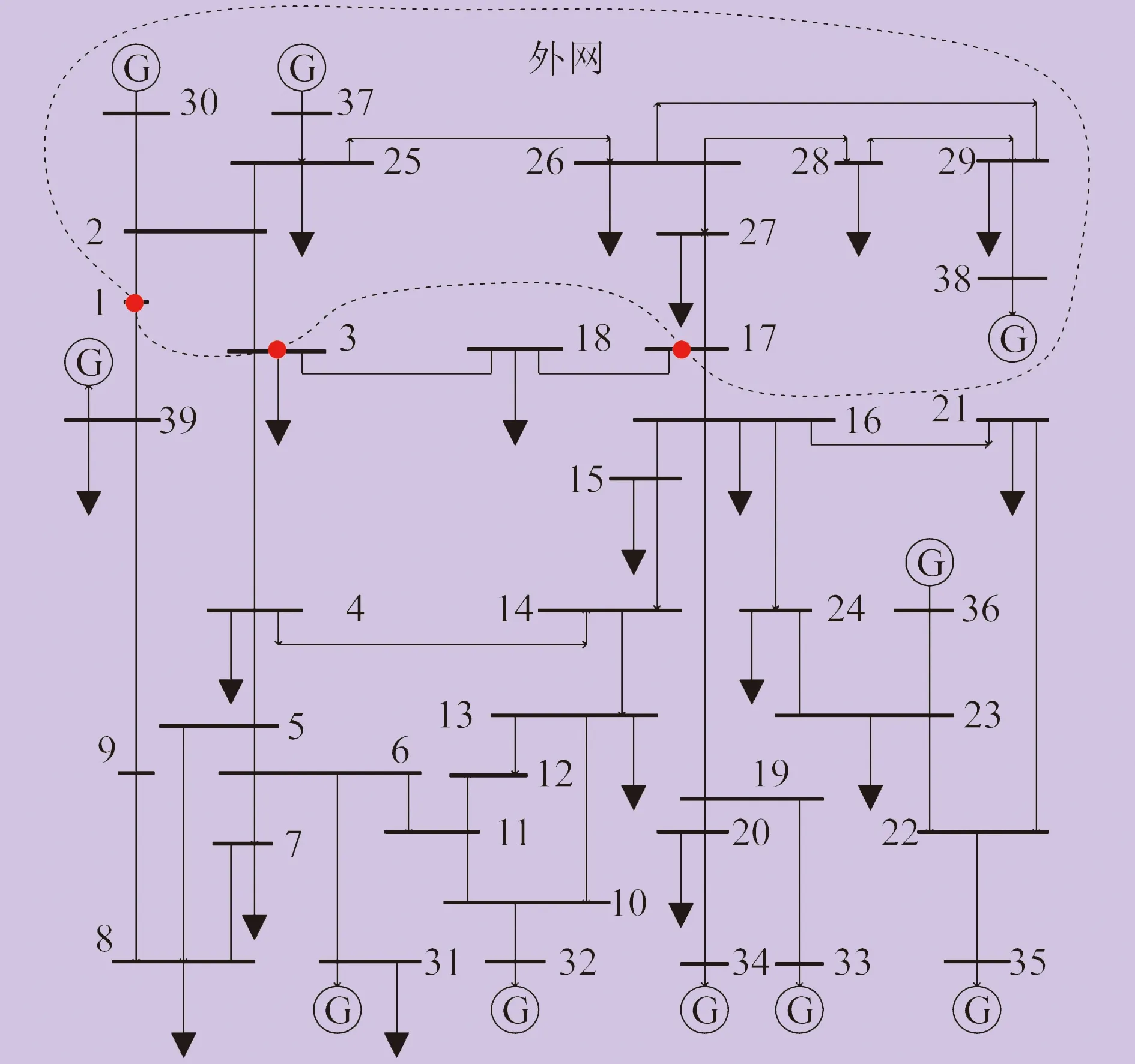
图4 IEEE 39节点系统

上述仿真条件下,IEEE 39节点系统等值网络参数估计收敛情况见表1。可以看出,方案一第一时段测量值与第二时段测量值变化百分比均值小于0.01%,造成等值网络参数估计不收敛,需在第二时段叠加功率扰动,功率扰动信息见表2。

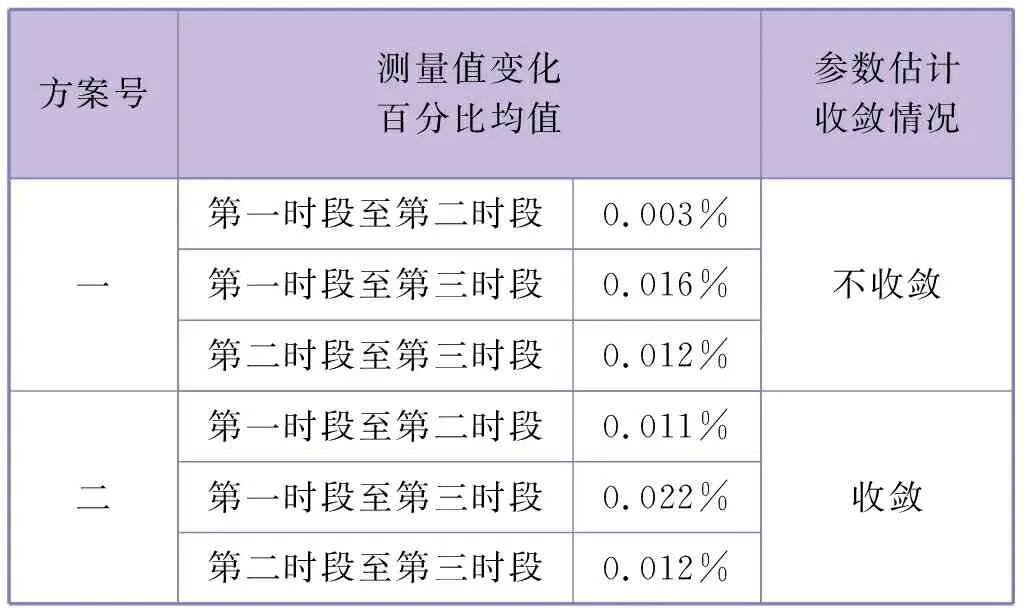
表1 IEEE 39节点系统参数估计收敛情况

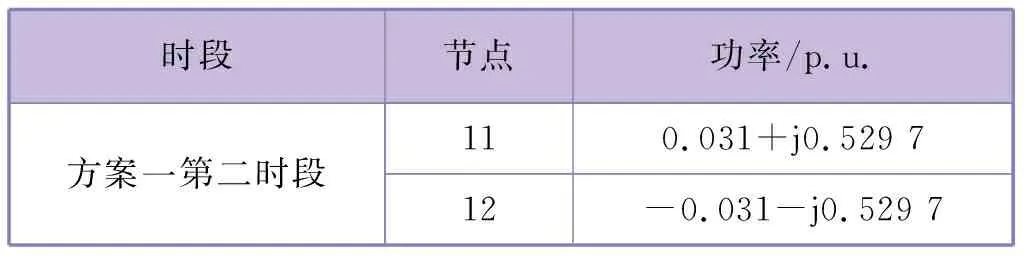
表2 IEEE 39节点系统功率扰动信息

在获得等值网络参数后,利用等值模型计算内网的潮流分布,并与未等值的全网潮流计算结果进行对比,以验证笔者构建等值模型的精度。由于大多数等值网络目前均为基于Ward等值,因此进行Ward等值对照仿真试验,比较验证笔者等值方法的精度。

为了研究测量噪声对等值结果的影响,在上述潮流结果为测量信息的基础上分别叠加标准差为σ的高斯白噪声,电压幅值、支路功率的测量误差标准差均为0.004,比较测量噪声对不同方法计算精度的影响。

采用潮流平均相对误差和最大误差两个等值误差评价指标,以比较不同方法的等值精度。

潮流平均相对误差ξave为:

(11)

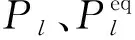
潮流最大相对误差ξmax为:

(12)

通常情况下,等值网络并不能精确代表外部电网,特别是当潮流状态相对基本状态有较大变化时,等值后的网络潮流误差较大。为使仿真结果具有代表性,假设在等值过程中电网负荷水平发生了变化。当负荷水平变化为零时,潮流状态相对基本状态保持不变。在线等值采用实时测量数据进行等值,时间跨度不大,通常在5 min以内。该时间段内,除特殊情况外,负荷水平变化一般不超过1%,因此选择负荷水平变化0、1%、3%时的潮流误差来验证笔者等值方法的有效性。

在没有测量噪声的情况下,不同负荷水平下的等值模型潮流平均相对误差和最大误差见表3。

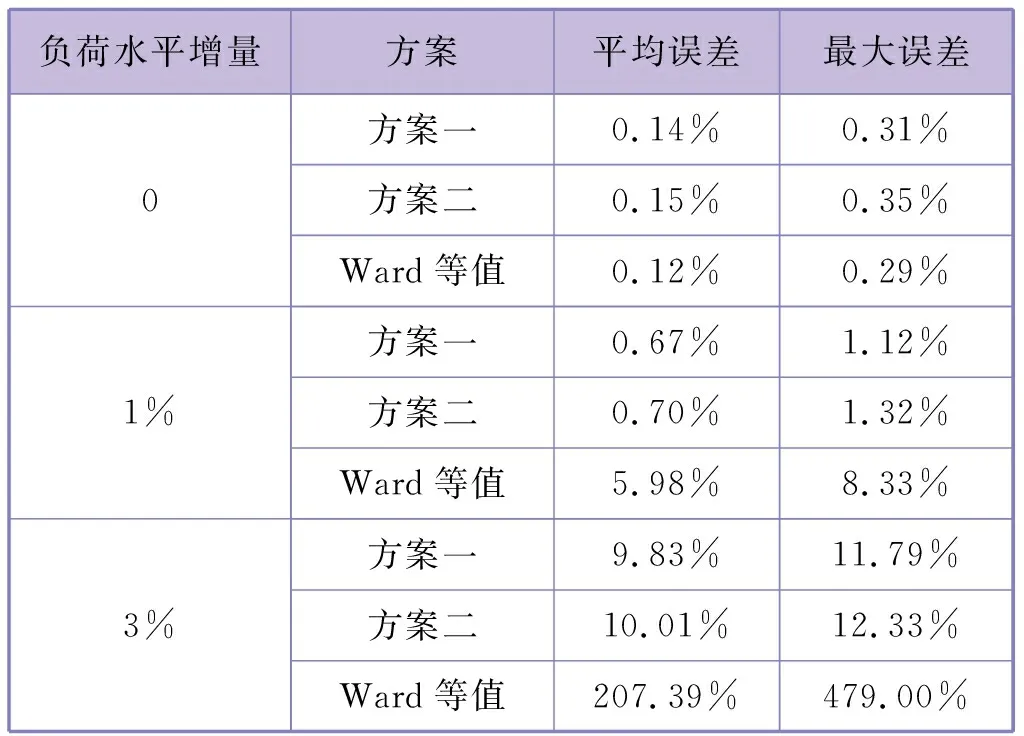
表3 不同负荷下IEEE 39节点系统等值模型潮流误差

可以看出,在全网状态不发生改变的情况下,基于初始状态全网数据进行Ward等值所得的模型误差最小;当负荷水平发生变化时,Ward模型的误差远大于笔者等值模型。这是因为Ward等值是根据初始负荷水平下潮流状态进行等值的,其等值结果能够准确代表电网状态不发生任何改变时的外部电网;当电网状态发生变化时,基于初始状态潮流的Ward等值结果不能准确代表外部电网,甚至由于等值网络的误差加大了内部电网的潮流误差,造成内部电网潮流平均相对误差和最大误差两个指标明显增大。由对比可知,笔者所提等值模型更适应潮流状态变化的实际情况。

内网测量信息具有测量误差时,Ward等值模型和在线等值模型的等值误差见表4。

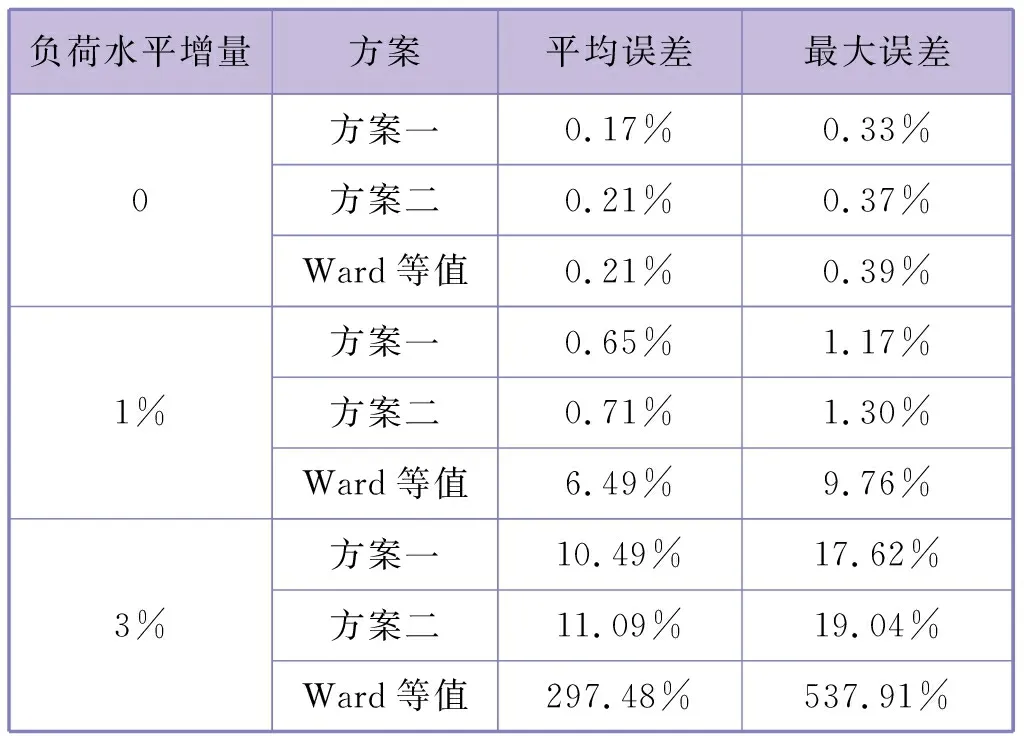
表4 测量误差影响下IEEE 39节点系统等值模型潮流误差

对比表3和表4可以看出,Ward等值受测量误差影响更大,笔者所提等值模型虽然在测量误差的影响下潮流误差相对于无测量误差时有所增大,但在电网状态变化不大时仍然能够保持较高的精度,负荷水平变化低于1%时潮流平均误差严格控制在1%以内。

5 结束语

笔者提出基于内网测量信息,由功率扰动获取补充测量信息的外网在线等值新方法。这一方法基于边界节点多个时段的测量信息,构建外网等值网络及相应的参数优化辨识模型。模型以等值网络边界节点多时段的计算值与测量值失配量最小为目标函数,使等值网络在边界节点的计算值最接近于测量值。采用基于补偿法叠加节点功率扰动获取补充测量数据的方法,有效提高了在线等值网络参数求解的稳定性。通过算例证明了这一方法的有效性。这一方法模型完善,计算稳定可靠,有望应用于实际工程。