电梯层站指示器装配车间调度优化算法*

钟臻怡,杨家荣

上海电气集团股份有限公司中央研究院 上海 200070

1 研究背景

电梯行业具有定制化生产、产品种类多、产品精度高、生产压力大等特点。大多数电梯生产过程中的调度问题已被证明是NP难问题,进而给电梯生产系统建模和优化调度带来较大困难。电梯生产过程中的调度问题是学术界和工程界的研究热点。

目前,电梯行业在生产调度管理和智能排程领域的研究仍处于发展阶段。赵瑛[1]对电梯产品钣金车间的调度问题进行研究,提出了基于工艺流程矩阵的静态调度优化方案,并引入周期性设备状态査询方案,建立动态调度优化模型。张静[2]通过生产排产知识、约束理论及现场管理理论,在排产前确认瓶颈工序,设定系统缓冲,进而优先确定瓶颈工序排程计划和非瓶颈工序排产计划。孙加洲等[3]运用启发式算法,动态进行主生产计划排程,解决了电梯生产过程中多个工作中心生产的同期成套问题和生产负荷平准问题。李彦君[4]提出一种基于生产计划驱动,合理考虑生产资源负载状况的生产管理系统,按生产计划和设定的原则进行调度排产计算,均衡分配生产任务。豆之敬[5]研究了电梯轿厢生产车间调度策略,采用阶段进化的自适应遗传模拟退火算法,可以避免传统遗传算法过早收敛及后期搜索效率低等问题。曹成辉[6]以山东某电梯公司机械加工车间为研究对象,对柔性作业车间调度问题进行深入分析,提出自适应文化遗传算法。试验结果表明,这一算法可以有效解决调度问题。孙斌[7]对单目标柔性作业车间调度问题进行研究,采用基于工序和机器的双层编码方式,以及分步更新的策略,进行萤火虫位置的更新,并采用病毒感染操作加强群体的协作能力和动态搜索能力。通过与遗传算法、粒子群优化算法进行比较,验证了这一方法的有效性。陈少[8]分析了电梯零部件排产过程的特点,提出通过改进鸟群算法求解柔性化电梯零部件排产问题,并利用调度规则求解动态扰动后的重排产问题,同时采用反向传播神经网络作为推理手段,选择出适合生产情况的最佳调度规则。

通过对上述电梯行业车间调度文献进行分析可知,在问题域方面,文献主要以柔性作业车间的电梯调度问题作为研究对象,如电梯轿厢生产车间、电梯机械加工车间等,且暂无研究电梯层站指示器装配车间的调度问题。在排程方法方面,上述文献使用了基于经验规则的启发式算法或以遗传算法为代表的元启发式算法。笔者针对电梯层站指示器的特点,将启发式规则和元启发式算法相结合。利用启发式规则对具有相似产品结构的订单进行合并,以此降低物料切换频率,缩短配料时间。使用分布估计算法进行优化调度,解决电梯层站指示器多订单、小批量、物料切换频繁、备料时间长等问题,提高车间的装配效率,有效缩短订单的总完成时间。

2 调度问题描述

电梯层站指示器车间装配线上共有J种不同类型的订单待装配,有M条处理订单能力不同的装配线,每种订单的产品大小不同,装配时间也不同。订单在物料到达之后和装配之前首先需要进行配料,并且不同订单种类物料到达时间和配料时间也均不相同。

在本调度问题中,假设J种订单中的每一种均可由M条装配线中的一条完成装配任务,每条装配线在每一时刻只能装配一种订单,一种订单一旦在装配线上进行装配,就不能中断,直至装配完成。

针对这一电梯层站指示器装配车间调度问题,通过合并订单缩短配料时间,并以实现最短加工周期为调度目标,进行装配车间的调度优化。

3 数学模型

在研究中,定义相关参数符号。i、j、k为订单序号,m为装配线序号,aj为订单j的物料到达时间,pj为订单j的配料时间,tjm为订单j在装配线m上的装配时间。

定义决策变量xij。如果订单j在同一条装配线上接着订单i装配,那么xij为1,否则xij为0。虚拟变量job0表示物料到达时间、配料时间和装配处理时间均为零的工件,这样就能够表示一条装配线开始装配和结束装配的状态。

根据上述问题描述、模型假设、参数、决策变量等,对所研究的梯层站指示器装配车间调度问题进行建模。

目标函数为生产过程时间最短,即minCmax。

约束条件式(1)、式(2)表明装配线开始和结束的状态出现次数总和均不大于M,即订单被分配到M条装配线中的一条:

(1)

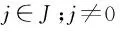
(2)

约束条件式(3)、式(4)表明在任意订单的紧前、紧后,订单有且仅有一个,用于分配装配线及订单在同一条装配线上的顺序:

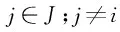
(3)

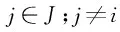
(4)

约束条件式(5)表明订单i完成时间Ci的范围:

∀i∈J,∀j∈J:j≠0,i≠j

(5)

式(5)中Q满足:

(6)

4 算法构建

4.1 启发式规则

由于电梯层站指示器物料种类繁多,每种订单所需的物料型号及数量均不相同,因此配料时需要进行频繁的物料切换,从而导致大量分拣操作。笔者根据计划订单物料清单一级分解表,利用启发式规则对具有相似产品结构的订单进行合并,降低物料配送频率,从而大大缩短配料时间。

在电梯层站指示器订单编码中,具有产品参数、印板图号、印板参数、按钮参数等信息。为了降低物料配送频率,设计启发式规则对印板图号和印板参数一致的订单进行合并,从而将印板相同的产品合并成一种订单集中装配,缩短印板的切换和配料时间。

4.2 分布估计算法

分布估计算法是一种新颖的进化算法,在优化过程中应用了概率分布模型[9]。

在订单完成合并后,笔者运用分布估计算法进行调度优化。

(1) 编码。订单序号的排列作为本调度问题的一个解,π={π1,π2,…,πj}表示订单装配顺序,πj为第j种待装配的订单。

(2) 解码。按照装配线分配规则依次完成所有订单,装配线分配规则为选择订单最早结束装配的装配线。假设rm为装配线m最早未占用的时间,则最早结束装配的时间为min{max{rm,aj}+pj+tjm}。

(3) 初始化种群。为了保证初始种群的分散性,采用随机初始化方法产生均匀分布的N个个体作为初始种群。

(4) 概率模型。分布估计算法通过对概率模型采样产生下一代。概率模型用概率矩阵P表示。元素phj(G)为第G次迭代中订单j在第h个位置上或之前出现的概率。算法选择种群中目标值最小的S个个体作为优势群体,S为η与N的乘积,η为优势种群占整个种群的比例。概率矩阵P根据式(7)进行初始化:

(7)

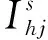
(5) 概率模型的更新。采样产生N个新个体之后,选择目标值最小的S个个体作为优势群体,并根据式(8)更新概率矩阵P:

phj(G+1)=(1-α)phj(G)

(8)

式中:α为概率矩阵P的学习速率,α∈(0,1)。

(6) 基于Insert函数和首次改进跳出原则进行局部搜索。为了平衡算法的全局和局部搜索能力,基于Insert函数和首次改进跳出原则局部搜索。

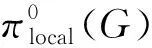
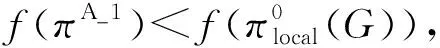
算法流程如下:

步骤1,编码并初始化种群,初始化概率矩阵P;

步骤2,解码并产生新种群,选择优势群体;

步骤3,更新概率矩阵P;

步骤4,进行局部搜索;

步骤5,如果终止条件没有满足,那么重做步骤2,否则停止。

5 试验分析

5.1 参数设计

试验通过加工周期值和中央处理器占用时间来衡量结果,设最大迭代次数为300。

笔者对计划下达的订单进行合并,大大减少了订单种类,由此缩短了配料时间。试验通过遗传算法[10]、粒子群优化群法和笔者提出的分布估计算法来求解各种不同规模的电梯层站指示器装配车间调度问题的性能。问题实例随机产生如下:订单种类集合为{10,20,50},装配线个数集合为{2,4,6}。每种订单的数量、装配时间分别由[1,20],[2,6]离散均匀分布随机产生。共有九种规模,对每种规模随机产生和测试十个不同的实例,因此本试验共产生和使用90个测试实例。

5.2 试验结果

试验结果见表1和表2。加工周期试验结果中,分布估计算法平均值为3 779.32,遗传算法平均值为3 893.17,粒子群优化算法平均值为3 878.38。中央处理器占用时间试验结果中,分布估计算法平均值为53.21 s,遗传算法平均值为16.34 s,粒子群优化算法平均值为16.58 s。

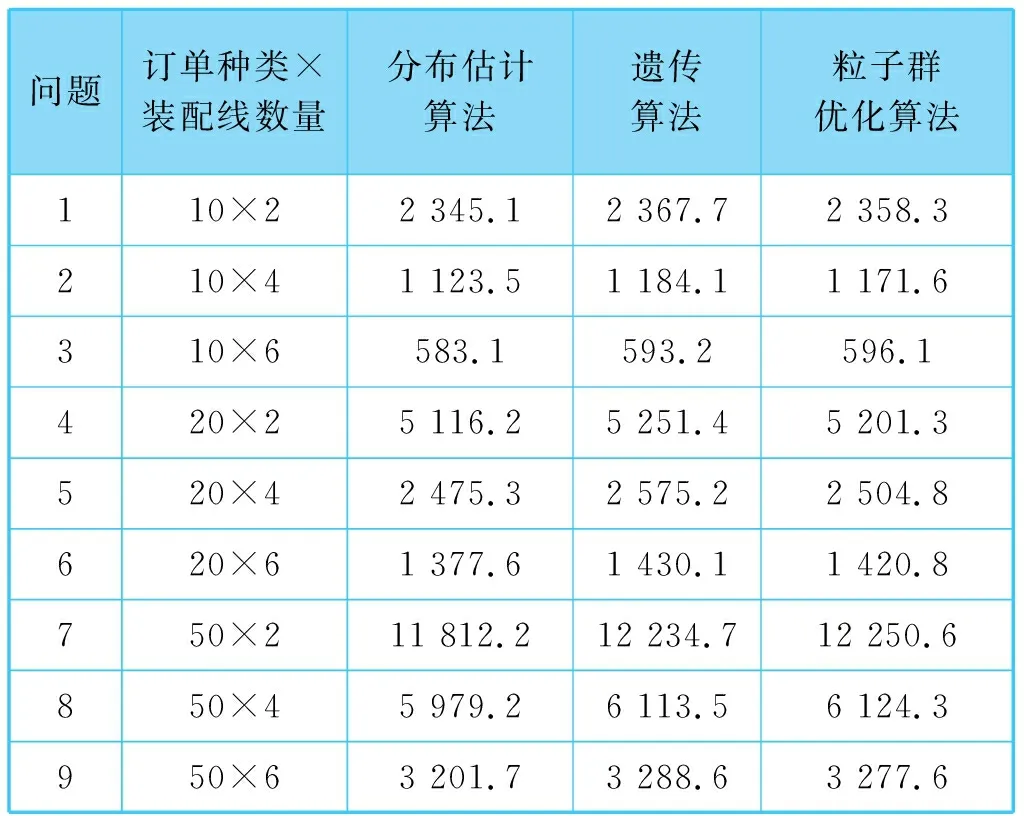
表1 加工周期试验结果

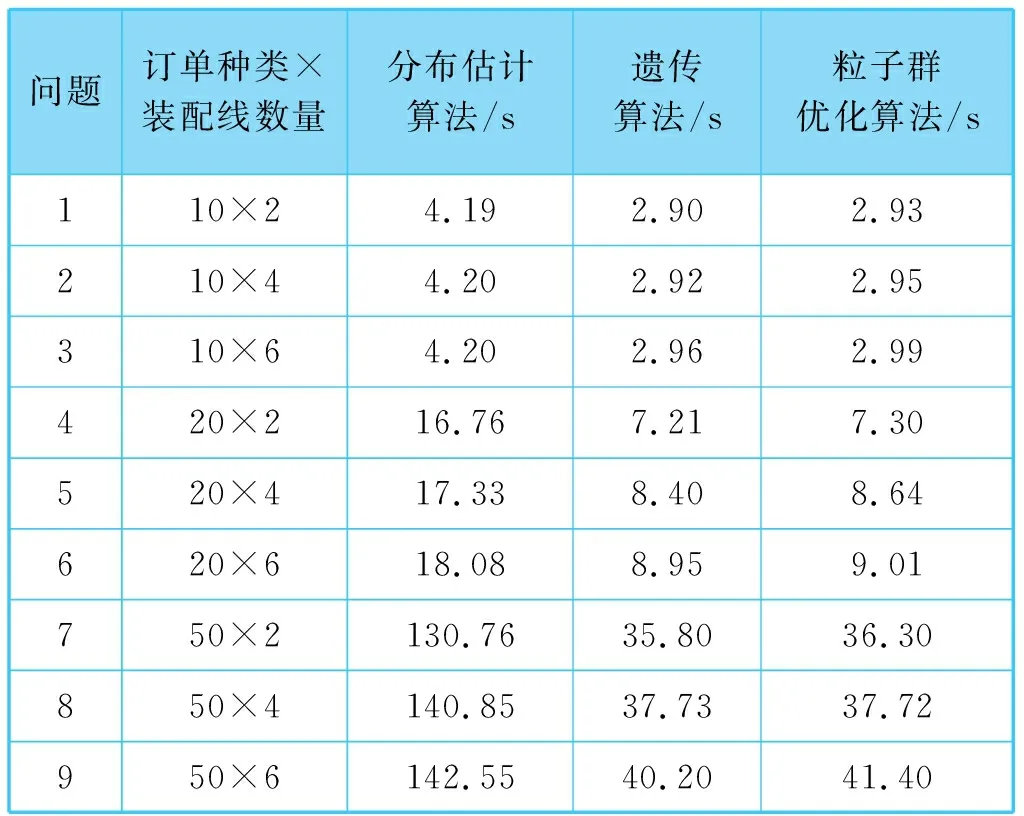
表2 中央处理器占用时间试验结果

表2中,遗传算法和粒子群优化算法在中央处理器运行时间方面更有优势,这是由于遗传算法和粒子群优化算法产生下一代的复杂度为线性,而分布估计算法的复杂度为二次方。表1中,分布估计算法在解的质量方面优于遗传算法和粒子群优化算法。可见,分布估计算法针对所有规模问题在三个算法中都表现得最好,并且中央处理器占用时间也是可以接受的。

6 结束语

笔者以电梯层站指示器装配车间调度问题为研究对象,针对装配车间订单多类型、小批量、物料切换频繁、备料时间长等特点,提出了电梯层站指示器装配车间调度的问题域,建立了以加工周期最短为目标的数学规划模型,利用启发式规则对具有相似产品结构的订单进行合并,以此降低物料切换频率,缩短配料时间。在研究中,提出了基于分布估计算法的调度优化方法,设计了针对装配车间调度优化的解码规则,并引入了基于Insert函数和首次改进跳出原则的局部搜索功能。试验结果表明,这一分布估计算法在各种规模下均能比遗传算法和粒子群优化算法更有效地解决电梯层站指示器装配车间调度问题。