基于Crank-Nicolson差分与Newton迭代法的非线性热传导方程数值解法

高忠社

基于Crank-Nicolson差分与Newton迭代法的非线性热传导方程数值解法

高忠社

（天水师范学院 数学与统计学院，甘肃 天水 741001）

非线性热传导方程；隐式Euler差分法；Crank-Nicolson差分格式；Newton迭代法

1　非线性热传导方程

文献[1-3]给出了一般形式的非线性热传导方程及数值解法．非线性热传导方程为

对方程（1）进行化简，可得到

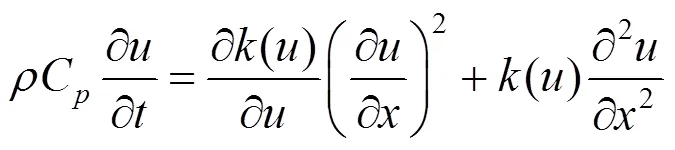
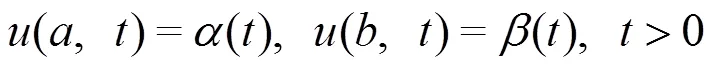
其中，边值条件（3）是在区间两端关于时间的温度分布函数，初始条件（4）表示在初始时刻的温度分布情况．本文对方程（1）在时间方向上使用隐式EULER 差分格式，空间方向上使用Crank-Nicolson差分格式，对于离散化后的代数方程组，使用NEWTON迭代法进行求解．

2　时间方向的隐式Euler方法离散

对于方程（4），在时间方向上利用隐式EULER方法离散化，得到

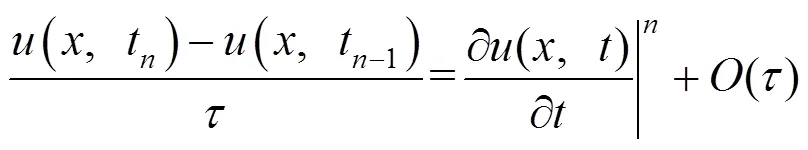
则式（6）变为

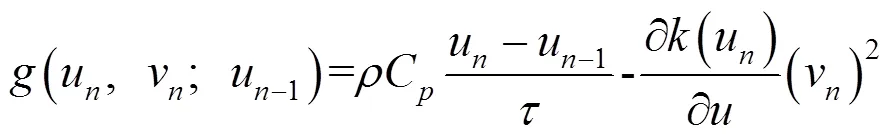
边值条件离散为

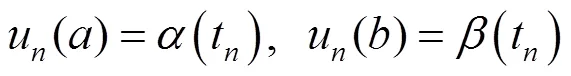
3　空间方向的Crank-Nicolson差分格式方法离散

对于式（8）的二阶导数使用二阶中心差分算子，得到

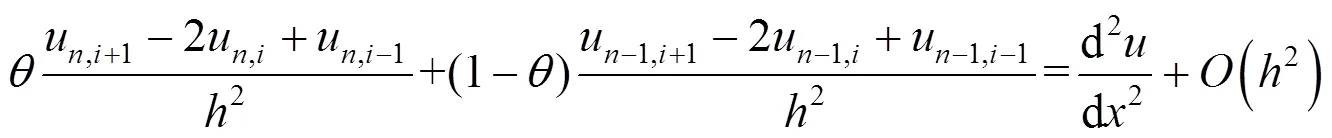
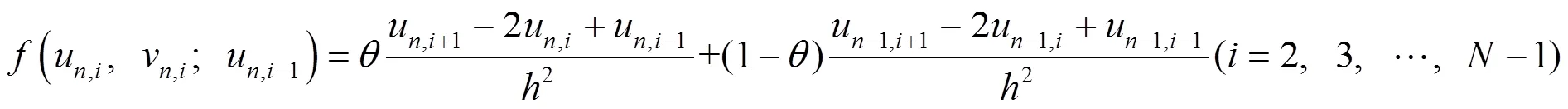
设

其中

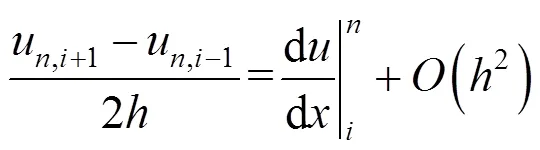
根据式（11）（14），有

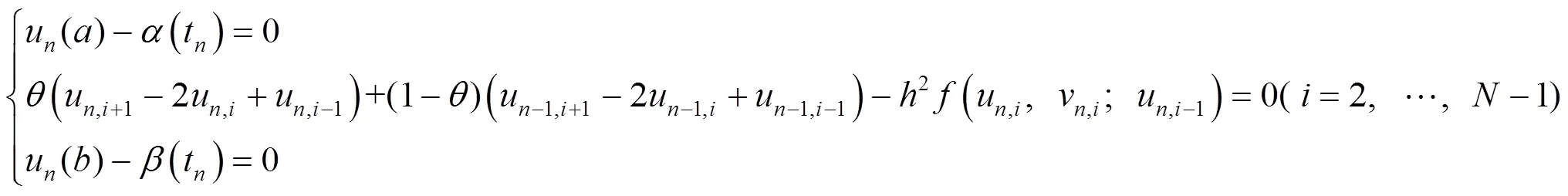
4 差分格式的误差分析

根据文献[8-10]，对于差分格式进行误差分析，由式（7）（13）（16）可知

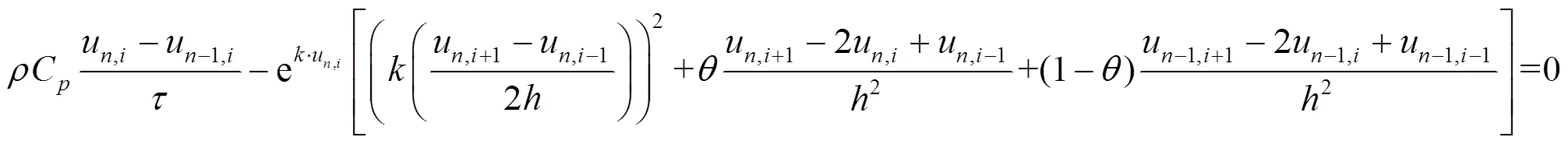
对于式（18）中各项使用Taylor级数展开，则有

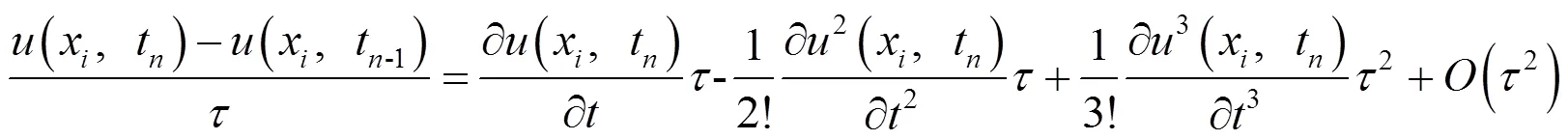
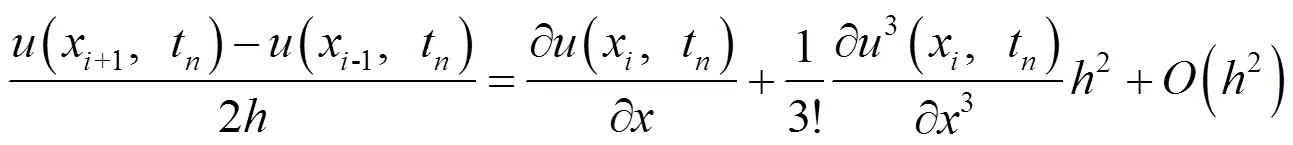
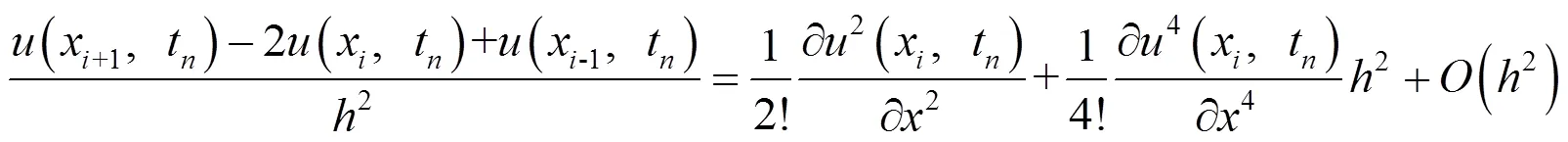
将式（19）（20）（21）代入式（18），整理化简可得截断误差为

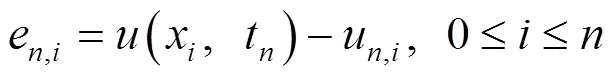
5　非线性方程的牛顿迭代法求解

记方程（23）为

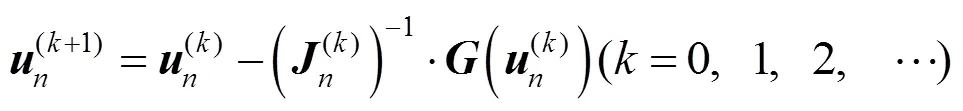
综上分析，可得Jacobian矩阵的元素为

6　数例分析

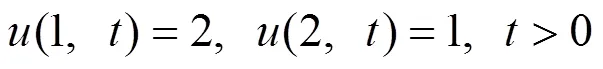
初始温度分布满足

图1　导热参数时的热传导三维图形和对平面图形

图2　导热参数时的热传导三维图形和对平面图形

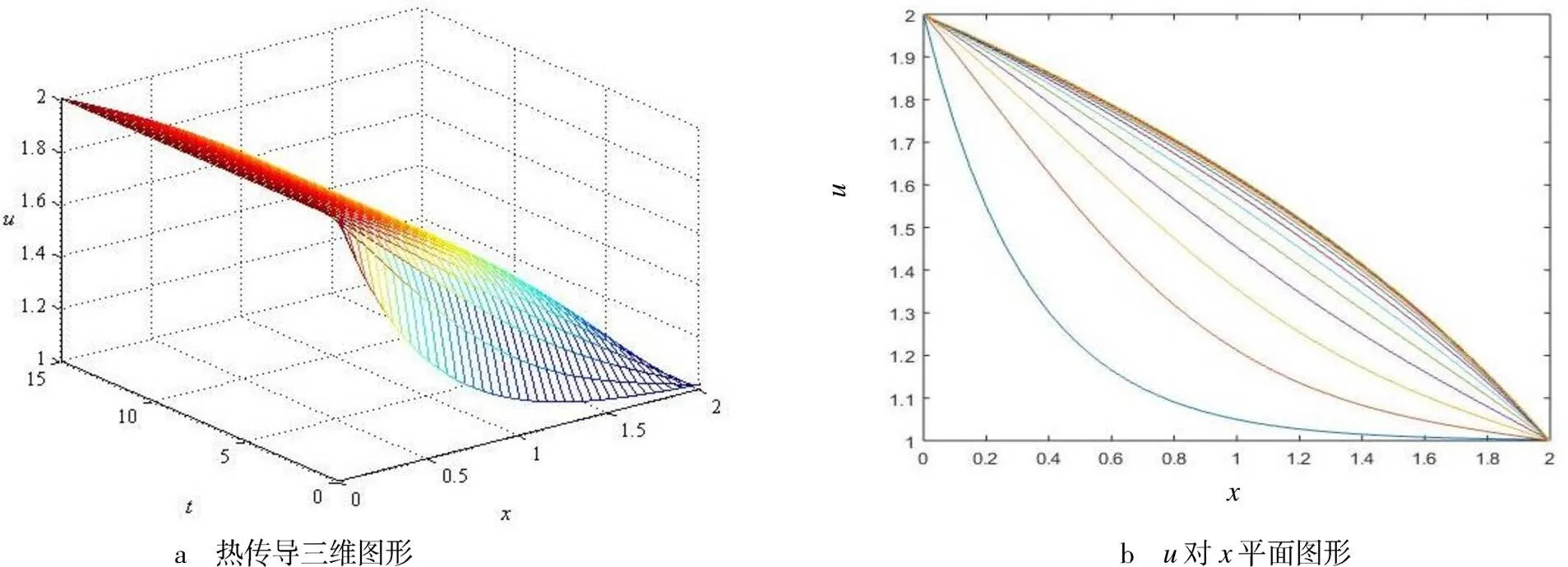
图3　导热参数时的热传导三维图形和对平面图形

由图1~3可以看出，热量在原点处具有最高温度分布，随着时间、空间方向的变化温度降低，符合热传导规律，说明本文所给的数值方法是合理、有效的，同时也说明该方法具有一定的实用性与可行性．

热传导方程的数值解法是抛物型方程求解的典型方法，同时热传导问题也被广泛应用于多个科学工程领域．针对非线性热传导方程，本文在时间方向上使用隐式Euler 差分格式，空间方向上使用Crank-Nicolso格式对方程进行离散化，离散化后的代数方程组使用Newton迭代法进行求解，最后通过数值算例分析讨论，说明该方法具有一定的实用性和有效性．

[1] Filipov S M，Faragóid S C．Implicit Euler time discretization and fdm with newton method in nonlinear heat transfer modeling[J]．arXiv，2018：1811.06337

[2] Carslaw H S，Jaeger J C．Conduction of heat in solids[M]．New York：Oxford University Press，1986

[3] Lienemann J，Yousefi A，Korvink J G．Nonlinear heat transfer modeling，in: p. benner，d.c.sorensen，v.mehrmann（eds） dimension reduction of large-scale systems[J]．Lecture Notes in Computational Science and Engineering，2005（45）：327-331

[4] Ascher U M，Mattjei J，Russel R D．Numerical solution of boundary value problems for ordinary differential equations[J]．Classics in Applied Mathematics，1995（13）：28-83

[5] Filipov S M，Gospodinov I D．Shooting-projection method for two-point boundary value problems[J]．Applied Mathematics Letters，2017，72（10）：10-15

[6] 王晓峰，王军涛．N-S方程的完全四阶紧致差分格式[J]．高师理科学刊，2017，37（2）：1-3

[7] 武莉莉，祁应楠．三维热传导方程的高精度有限差分方法[J]．数学的实践与认识，2017，47（20）：187-195

[8] 李继军，张华峰．波动现象的时域有限差分法模拟[J]．高师理科学刊，2017，37（12）：35-39

[9] 孙志忠，偏微分方程数值解法[M]．2版．北京：科学出版社，2012

[10] 李治平，偏微分方程数值解讲义[M]．北京：北京大学出版社，2010

Numerical solution of nonlinear heat conduction equation based on Crank-Nicolson difference and Newton iterative method

GAO Zhongshe

（School of Mathematics and Statics，Tianshui Normal University，Tianshui 741001，China）

nonlinear heat conduction equation；implicit Euler difference method；Crank-Nicolson difference method；Newton iterative method

O241.82

A

10.3969/j.issn.1007-9831.2020.11.003

1007-9831（2020）11-0009-05

2020-06-01

国家自然科学基金项目（11561060）；甘肃省数学省级重点学科建设项目（甘学位[2018]15号）；甘肃省教育科学“十三五”规划2020年度项目（GS[2020]GHB4815，GS[2020] GHB4825）；天水师范学院科研基金项目（CXT2019-36）

高忠社（1979-），男，甘肃宁县人，副教授，硕士，从事小波分析及微分方程数值解研究．E-mail：gaozhongshe@126.com