考虑异质性的经典随机后悔最小化模型改进研究

杨 飞，侯宗廷，周 涛

(1.西南交通大学交通运输与物流学院，成都611756；2.重庆市交通规划研究院，重庆401147)

0 引 言

目前，基于随机效用最大化理论(Random Utility Maximization，RUM)的离散选择模型在出行行为分析领域应用最为广泛.这类模型假设人们在做选择时采用完全理性的决策原则.然而，Simon 等[1]对完全理性的决策假设提出质疑，认为由于有限的认知能力和各种心理因素，个体在做选择时受到理性约束.后悔理论由Bell等[2-3]提出，该理论认为决策者是有限理性的，在做选择时，他们更倾向于追求期望后悔最小化.在出行行为研究中，后悔理论关注的是出行者在做决定时的心理状态，根据出行者的行为特征和心理偏好更好地描述出行决策行为.因此，后悔理论逐渐成为分析出行行为的新兴理论.Chorus等[4]提出随机后悔最小化模型(Random Regret Minimization Model，RRM)，被称为原始随机后悔最小化模型，在经济决策行为分析中经常使用的后悔理论被引入交通出行决策行为研究中；随后，Chorus 等[5-6]对原始RRM 模型进行修正与改进，提出经典随机后悔最小化模型(Classic RRM)，定义了多方案和多属性决策中的后悔值，提出利用RRM理论建立离散选择模型的新方法，着重分析基于RRM 的多项式Logit(RRM-MNL)模型，结果表明，RRM-MNL 模型能更好地描述选择决策过程中的半补偿原则和折中效应.半补偿原则是多方案和多属性决策中一个重要的基本概念，即当一个选择方案的某个属性大幅提升带来的影响不能全部抵消该方案另一个属性大幅下降所带来的影响.折中效应是指在现实的决策行为中，人们更倾向于所有属性都处于中间值的选择.折中效应在很多研究领域得到验证，但在出行行为分析领域却鲜有研究.鲜于建川等[7]建立RUM-MNL 模型和RRM-MNL 模型分析城际出行行为，并比较两种模型的参数和拟合优度，结果表明，RRM-MNL 模型能较好地描述半补偿效应和折中效应，能较好地反映真实的出行选择行为.而基于后悔理论的城市交通选择行为实证研究还比较缺乏.

出行行为的关键在于所构建的模型是否符合实际情况及具有较强的解释能力.传统出行选择模型中，通常假设个体偏好是同质的.然而由于个体偏好、风险承受能力和个人经济社会属性等异质性影响，个体在面对同一选择时往往表现出不同的偏好[8].越来越多的研究表明，在出行行为研究中考虑个体异质性的影响能够提升模型的拟合优度和解释能力，可以更好地分析出行者的选择行为[9-10].影响个体出行方式选择的异质性通常包含两个方面：可观测的异质性变量，如年龄、性别、收入等个人社会经济属性；不可观测的异质性变量，如出行习惯、对出行方式的各属性主观感受等.传统基于后悔理论的选择模型对个体异质性考虑不足，对真实选择行为的解释存在差距.本文在经典随机后悔最小化模型中加入不可观测的异质性，即出行者对各方式属性变量感知异质性的影响对模型进行改进，分别建立基于随机效用最大化，经典随机后悔最小化和改进经典随机后悔最小化的选择模型，以网约车选择行为为例验证模型的改进效果，对比分析3种模型的参数标定结果及拟合效果，同时利用直接弹性分析对比不同参数在不同模型中的影响效果.

1 模型构建

首先，确定选择枝集合.基于成都市主要交通出行方式，考虑与网约车存在竞争关系的出行方式作为备选项，确定个体选择枝集合为常规公交、地铁、私家车、出租车、网约车.其次，确定影响选择枝效用的属性.根据实际情况设置候车时间、车内时间和费用作为出行特征属性.因后悔函数与效用函数形式不同，性别、收入、年龄等个人经济社会属性变量不能简单地线性加入后悔函数，因此，本文暂不考虑个人经济社会属性等可观测的个体异质性变量.

1.1 基于随机效用最大化的选择模型(RUN-MNL)

根据随机效用最大化理论，出行者总是选择具有最大出行效用的出行方式，出行者n选择第i种出行方式的概率为

式中：Uni为出行方式i对于出行者n的效用；Unj为出行方式j对于出行者n的效用；Cn为出行方式选择枝集合.

随机效用理论认为效用是一个随机变量，并将效用函数U分为可以观测的固定项V和不可观测的随机项ε两部分，假设它们呈线性关系.因此，出行方式i对出行者n的效用函数表示为

式中：Vni为出行方式i对出行者n的效用函数的固定项；εni为出行方式i对出行者n的效用函数的随机误差项；K为出行选择i所包含的属性数量；Xnik为出行者n的出行选择i所包含的第k个属性；θk为第k个属性所对应的未知参数.假设随机项服从Gumbel分布时，可得出RUM-MNL模型为

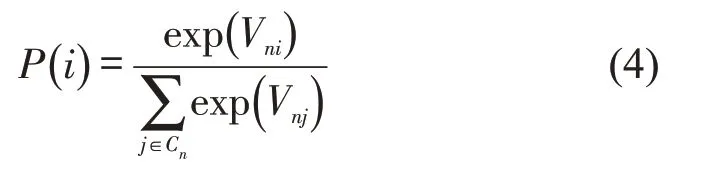
1.2 基于经典随机后悔最小化的选择模型(RRMMNL)

当出行者n面对I个出行方式选择时，每个方式i(i=1,2,…,I)受M个属性的影响，第m个属性为xnim(m=1,2,…,M).根据经典随机后悔最小化理论，出行者在I个方式中做选择时，会追求随机后悔最小的方式.方式i的后悔值Rrni由确定的系统后悔值Rni和随机误差项εni组成，即

确定的后悔值Rni为通过比较方式i和方式j(i≠j)得到的方式i的所有属性后悔值的总和，即

式中：Rnijm为方式i与方式j比较所得的属性后悔值；xnim、xnjm分别为方式i、方式j的属性m的值；βm为对应的参数.

因为决策者追求后悔值最小，取方式i的后悔值Rrni为Rni的相反数，假设随机误差项εni服从Gumbel分布时，决策者n选择方式i的概率Pni为

1.3 基于改进经典随机后悔最小化的选择模型(改进RRM-MNL)

出行者面临方式选择时，对不同方式属性表现的感知存在异质性.例如，人们对机票价格从1 500 元涨到1 510 元的10 元涨幅可以欣然接受，却很难接受地铁票价从5 元涨到15 元的10 元涨幅.经典随机后悔最小化模型中，用不同方式属性差值的绝对大小(xnjm-xnim) 考量出行者对不同属性的表现，未能考虑出行者对不同方式属性表现的感知异质性.本文引入韦伯定律对经典随机后悔最小化模型进行改进.韦伯定律由德国著名的生理学家与心理学家韦伯发现，是表明心理量和物理量之间关系的定律，即感觉的差别阈限随原来刺激量的变化而变化，而且表现为一定的规律性，刺激的增量和原来刺激值的比是一个常数，这个常数即韦伯比率[11]，表示为

式中：x为原刺激量；Δx为此时的差别阈限；c为常数.

改进模型中不考虑各方式属性差的绝对值，用韦伯比率对不同方式的属性表现进行考量.改进后后悔值函数的确定项Rni为

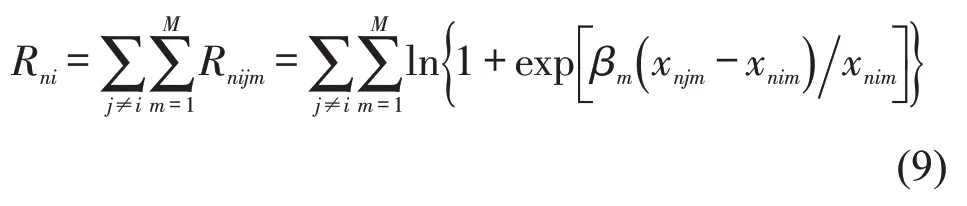
用方式i和方式j的属性m相比较的韦伯比率替代原模型中的(xnjm-xnim)表现不可观测异质性，即用不同方式属性差值和属性值相对大小反映决策者对不同方式属性表现感知的异质性.改进后模型的出行者方式选择概率计算与式(7)相同.

2 问卷设计与调查

2.1 问卷设计

为方便属性水平设置，本文选取成都市西南交大组团与天府广场组团间居民出行为研究对象.西南交大组团是以住宅为主的区域，天府广场组团是成都市商业和文化中心.联系两个组团间的主要出行方式包含先前确定的选择枝集合中的5种出行方式.根据实际情况确定的各选择枝属性水平如表1所示.利用正交设计，通过均衡搭配形成具有代表性和典型性的属性水平组合，最终生成16 个选择情境组成一套问卷.问卷同时采集了受访者的个人社会经济属性.

2.2 调查开展与样本分析

分别在西南交大组团和天府广场组团开展问卷调查，最终收集有效样本924 份.对有效样本进行整理分析，结果如表2所示.调查样本的年龄分布与抽样计划一致，男女性别比为0.97，平均收入为5 863元，与成都市统计年鉴中男女比例0.98，平均工资5 931元基本一致，抽样样本具有代表性.

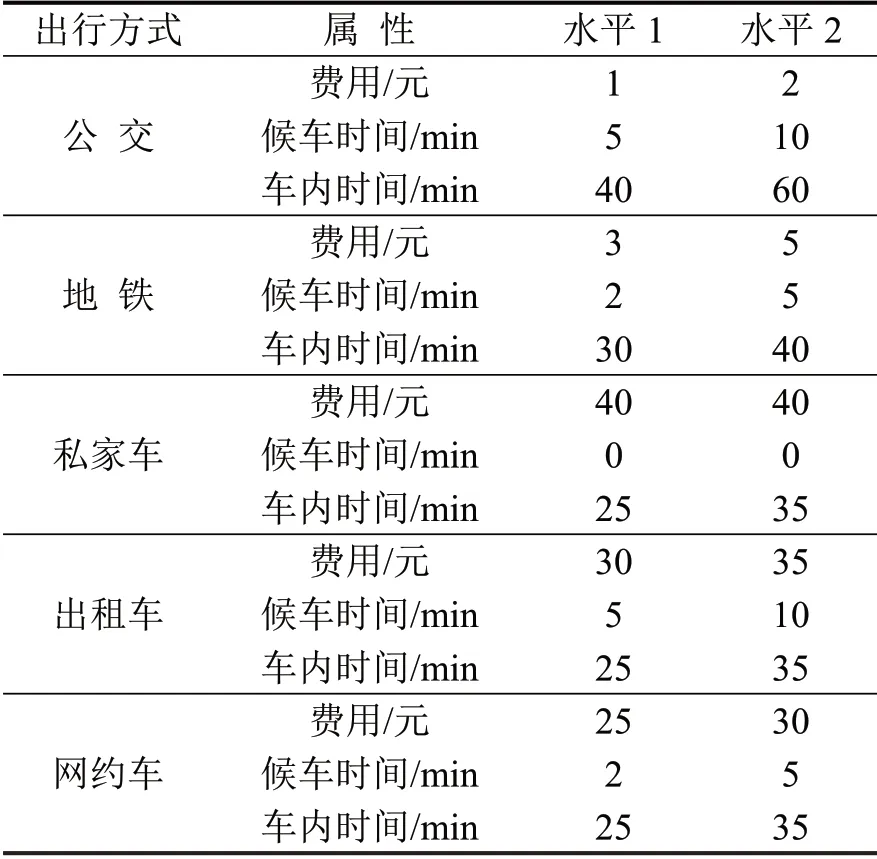
表1 属性水平Table 1 Level of alternative attributes

3 结果分析

3.1 参数标定结果及分析

为对比模型标定结果，利用BIOGEME软件编程采用极大似然估计方法对各选择模型进行参数估计，以私家车为参考项，标定结果如表3所示.通过T检验值检验各参数的显著性，T检验值绝对值大于1.96，即表示该参数在统计上显著.

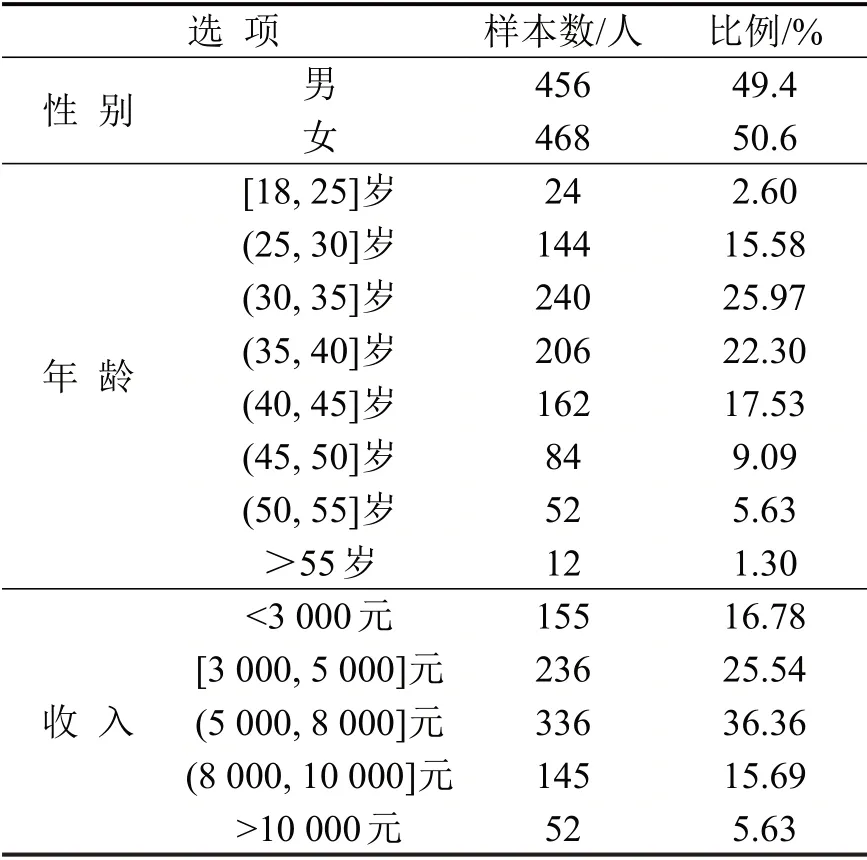
表2 样本统计Table 2 Statistical results of surveyed sample population

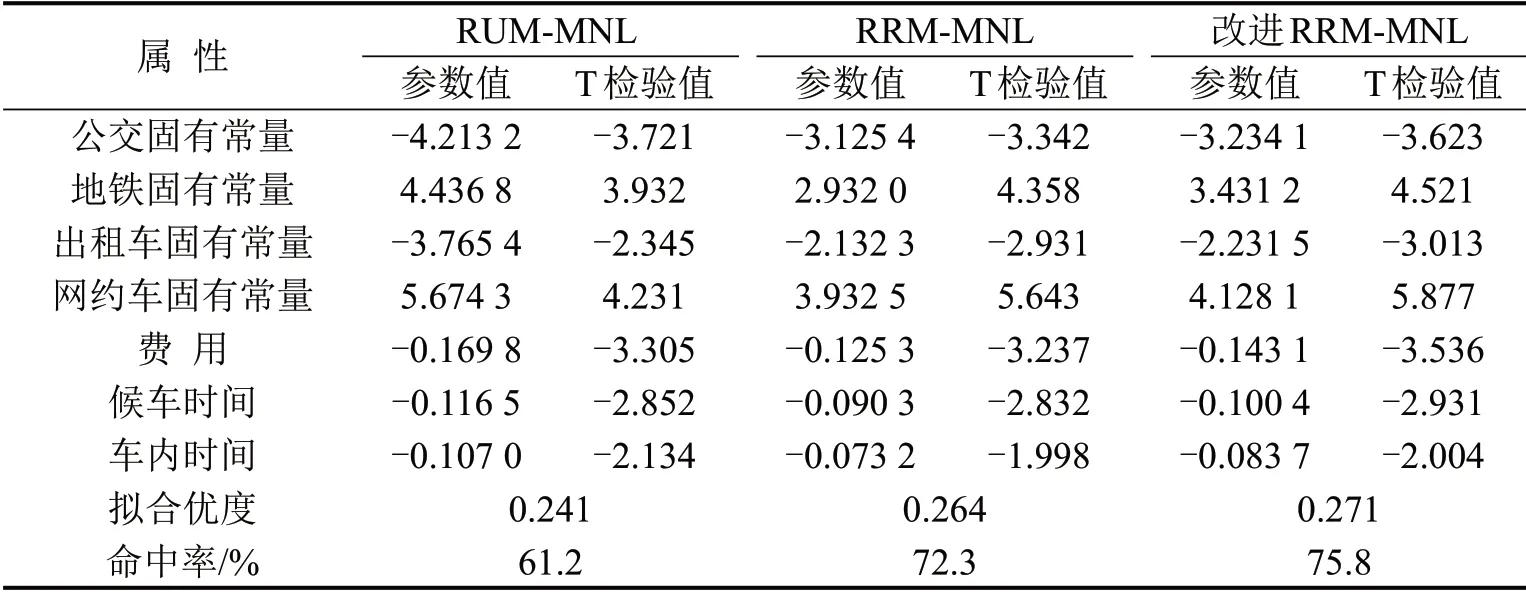
表3 模型标定结果Table 3 Model estimation results

由表3可以看出：

(1)3 种模型中，4 个选择枝的固定参数均显著，且参数符号一致，说明这4 种方式未被观测到的效用对其总效用各有影响.对比地铁和公交两种公共交通方式的固定参数，前者参数符号为正，后者为负，说明相较于私家车出行，地铁具有一定的吸引力，能够使部分出行者放弃私家车出行，但公交对私家车出行者吸引力不足.同理对比网约车和出租车两种小汽车出行方式的固定参数，前者参数符号为正，后者为负，说明相较于私家车出行，网约车具有一定优势让部分私家车出行转移到网约车，但出租车相对与私家车优势不明显.

(2)3种模型中，费用、候车时间及车内时间均显著且参数符号为负，说明这3 个变量值越高，选择该交通方式的概率越低，符合实际情况.其中，费用参数值绝对值最大，说明费用对出行者的方式选择影响最大.

(3)对比3 种模型的拟合优度和命中率可知，相较于RUM-MNL 模型，RRM-MNL 模型的拟合优度和命中率均有较大提升，说明基于个体有限理性假设的后悔理论更符合真实的决策过程.同时，改进RRM-MNL 模型的拟合优度和命中率相较于改进前均有所增加.因此，改进后模型解释能力更强，能更好地描述出行者真实的选择行为.

3.2 直接弹性分析

在RUM-MNL 模型中，由于效用函数的形式是线性叠加的，故方式i的属性l大幅增加的影响可以被属性m减少的影响抵消；而RRM-MNL 和改进RRM-MNL模型中，由于方式i的后悔函数不仅仅与自身属性相关，还与其他各方式的同种属性相关，故当方式i的属性l大大增加时所带来的影响并不能完全抵消方式i的另一个属性m减少所带来的影响，即半补偿效应.为描述两种决策行为的差异，分析属性变量对选择概率的直接弹性，即

3 种模型的属性变量对选择概率的直接弹性值计算结果如表4所示.

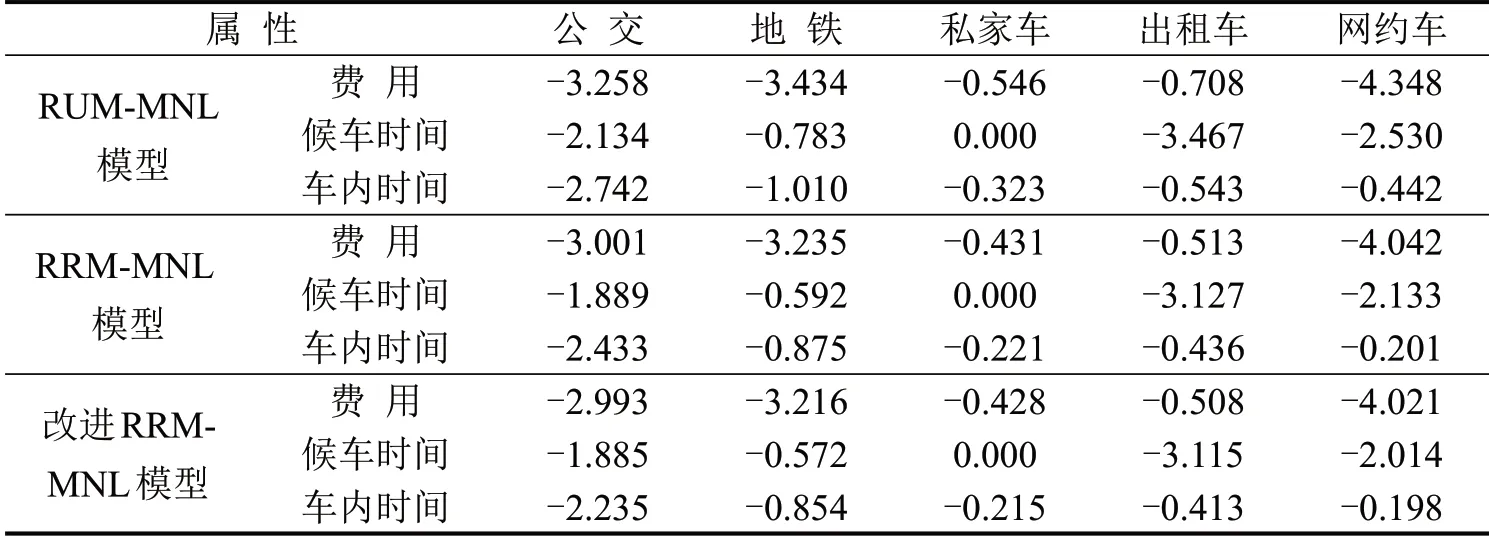
表4 直接弹性值比较Table 4 Comparison result of variable direct elasticities

由表4可以看出，基于随机效用最大化理论和基于经典随机后悔最小化理论的模型结果表现出显著性差异.以费用为例：RRM-MNL 模型中费用对各方式选择概率的弹性值绝对值均小于RUNMNL 模型，改进RRM-MNL 模型中弹性值的绝对值比改进前更小；费用对各方式选择概率的弹性均具有一致性，弹性值绝对值大于1，说明费用对公交、地铁和网约车的选择概率具有弹性；对比RUM-MNL 模型，RRM 模型中费用对公交、地铁、网约车选择概率的弹性绝对值分别降低了7.89%、5.79%和7.04%，改进RRM 模型中分别降低了8.13%、6.35%和7.52%；费用对网约车选择概率的弹性值符号均为负，说明费用的增加会降低出行者对网约车的选择概率，同时费用对网约车选择概率的弹性值绝对值最大，说明费用是影响网约车选择行为最重要的关键因素.假设网约车有优惠活动费用降低，由于弹性值的差异，不同模型预测得到的网约车选择概率增加的幅度存在差异.在RRM-MNL 模型中，在考虑所选择方式的属性比其他方式差的情况下，乘客会降低网约车费用对选择行为响应强度，这体现了两种模型在选择行为上决策原则的差异，改进后的RRM-MNL 模型能更好地反映这种差异性.其他变量的影响可以用类似的方法分析.

4 结 论

本文利用韦伯比率考虑出行者对各方式不同属性变量表现感知的异质性对经典随机后悔最小化模型进行改进，并以网约车选择行为为例分别建立基于随机效用最大化，基于经典随机后悔最小化和基于改进经典随机后悔最小化的选择模型，对比分析验证模型改进效果，主要结论如下：

(1)3种模型参数标定结果的显著性具有一致性，费用、候车时间及车内时间均对出行者的选择行为有重要影响，其中，费用的影响最为显著.3种模型的拟合优度均大于0.2，具有较强的解释力，能够较好地分析出行者的选择行为.

(2)改进后的经典随机后悔最小化模型的拟合优度相较于随机效用最大化模型及经典随机后悔最小化模型分别提升0.023和0.007，模型命中率分别提高11.1%和3.5%，说明改进后模型的解释力更强，能更好地描述出行者真实的决策过程.

(3)改进后经典随机后悔最小化模型中，个人属性变量对选择概率的直接弹性值绝对值相较于改进前及随机效用最大化模型最小，半补偿原则和折中效应得到了更好地描述.