城市轨道交通列车追踪间隔与牵引能耗优化
高 豪,郭 进,张亚东
(西南交通大学信息科学与技术学院,成都611756)
0 引 言
随着城市轨道交通大量新建线路投入网络化运营,我国轨道交通客运量增长明显,北京、上海两市日均客运量均已超过1 000万人.为满足日益增长的客运需求,以基于通信的列车运行控制(Communication Based Train Control,CBTC)为代表的移动闭塞系统取代了传统固定闭塞系统,并得到广泛应用.利用高精度列车定位、双向大容量车地无线通信等新兴技术,CBTC系统可以进一步提升高峰小时线路通过能力.据资料统计,2019年全国城市轨道交通高峰小时最小发车间隔平均为290 s,进入120 s 以内的线路共12 条.同线路能力一样,列车牵引能耗是制约城市轨道交通可持续发展的关键因素.面向高峰小时多列车密集追踪的运行场景,能耗问题尤为突出.在保证列车安全、正点运行前提下,通过调整列车操纵策略,进一步压缩行车间隔并减少牵引能耗,可有效提升城市轨道交通服务水平和经济效益.
针对多列车运行操纵优化问题,国内外学者开展了广泛讨论.Wang[1]面向固定闭塞和移动闭塞系统下的列车追踪运行场景,以最小追踪间隔为约束条件,研究列车运行受扰后的多列车节能操纵优化问题.Ye[2]考虑快慢车越行场景下的列车安全追踪及正点运行约束,通过构建多阶段优化控制模型求解多列车节能操纵最优策略.进一步地,柏赟[3]考虑追踪间隔要求和再生制动能利用,研究以列车净能耗最少为目标的快慢车线路列车协同操纵优化问题.Wang[4]在确保列车运行满足最小追踪间隔的前提下,通过调整各列车的站间运行时间来最大化多列车追踪优化的节能效果.以上文献将最小追踪间隔作为约束条件,研究不同场景下多列车节能驾驶优化问题.优化后的列车运行间隔发生改变,但线路能力并未得到本质提升.
Takeuchi[5]将最小追踪间隔作为衡量线路能力的性能指标,分析列车运行速度对最小追踪间隔的影响.陈荣武[6]通过调整车站限速区域及限速值压缩了近6.3%的列车最小追踪间隔.Nakamura[7]指出列车采用多级制动的进站操纵策略可有效压缩最小追踪间隔,并利用遗传算法优化列车进站操纵策略.上述文献将最小追踪间隔作为优化目标,通过调整列车操纵策略提升线路通过能力,却忽略了操纵策略改变带来的牵引能耗增加问题.
针对高峰小时地铁列车密集追踪运行的特点,本文同时将降低列车牵引能耗和缩短最小追踪间隔作为优化目标,通过优化列车操纵策略实现列车节能驾驶并提升线路通过能力.首先给出移动闭塞条件下列车牵引能耗和最小追踪间隔的计算方式,在此基础上考虑列车正点运行和线路限速约束,构建双目标优化模型;引入ε-约束法将模型转为单目标形式,并利用动态规划方法作进一步求解.
1 列车运行性能指标
1.1 列车牵引能耗
对运行过程中的列车进行受力分析,构建基于单质点的列车运动学计算模型,即

式中:M为列车质量;x为列车位置;v(x)为列车速度;α为回转系数;u(x)为列车牵引制动力;r(x)为列车运行阻力,包括基本阻力rb(x)和和附加阻力r1(x);rb(x)由戴维斯方程来表示,其系数a、b及c根据列车型号而定;r1(x)包括坡道附加阻力rg(x)、曲线附加阻力rc(x)和隧道附加阻力rt(x).
列车以操纵策略U={u(x)|umin(x)≤u(x)≤umax(x),x∈[0,X]} 在线路上追踪运行,其中,umax(x)和umin(x)分别为列车保证乘客安全、舒适条件下的最大牵引力和最大制动力,X为列车站间运行距离.列车执行U后的牵引能耗E(U) 和运行时间T(U)为
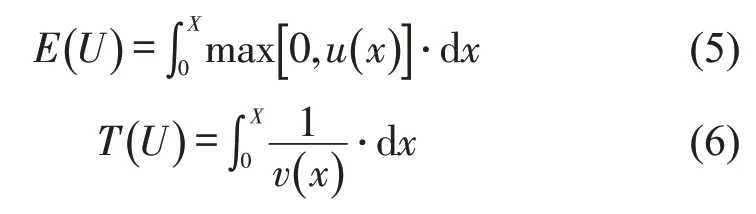
1.2 最小追踪间隔
线路通过能力体现为列车追踪运行过程中最小追踪间隔的倒数[5],取决于列车在线路最受限制点处的最小安全追踪距离及通过该距离的运行速度[6].移动闭塞系统中,相邻列车的间隔距离必须始终大于最小安全追踪距离.现有CBTC系统均采用不考虑先行列车速度的“硬撞墙”模型来计算最小安全追踪距离,即

式中:Smin(xa)为列车在位置xa处的最小安全追踪距离;Lreact(xa)为列车在反应时间Treact内的走行距离;Leb(xa) 为列车紧急制动距离;aeb为紧急制动率;Lsm为安全余量;Ltrain为列车车长.为简化计算,假设Treact、aeb、Lsm和Ltrain为固定值.
根据列车在通过最小安全追踪距离期间是否停靠站台,将最小追踪间隔的计算分为区间和车站两种模式.图1为区间最小追踪间隔示意,相邻两车以最小安全追踪距离为间隔分别运行至xa和xa+Smin(xa)处,其中,xa+Smin(xa)<xS,xS为站台位置.相邻列车沿图中实线所示的运行轨迹连续经过xa的最小时间间隔Hmin(xa)为

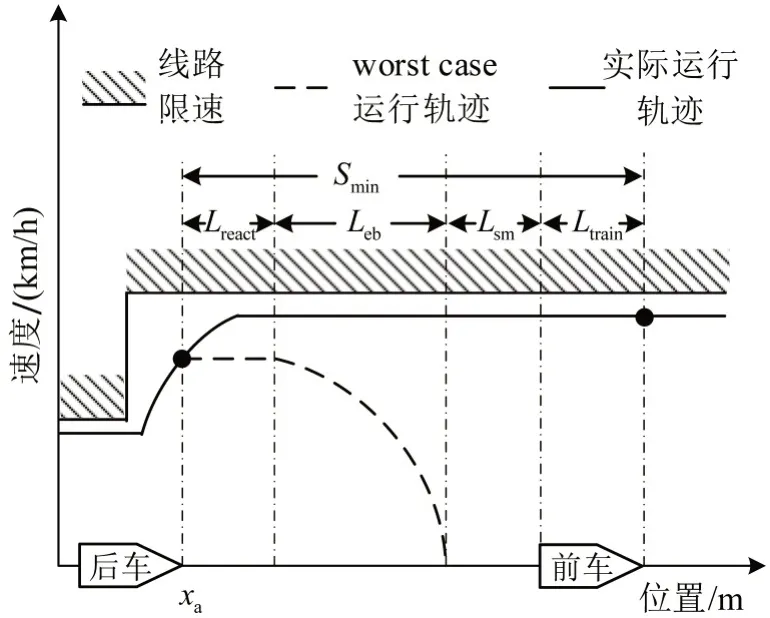
图1 区间最小追踪间隔Fig.1 Minimum headway of interstation
地铁车站一般不设配线,列车到达车站后需在正线上完成停站作业,且同一时间只允许1列列车进行停站作业.车站最小追踪间隔的计算不考虑存在多配线条件下的列车到达、到通、出发、发通等间隔,如图2所示.相邻两车分别运行至xa和xa+Smin(xa)处,其中,xa+Smin(xa)≥xS,列车通过Smin(xa)期间需经历减速进站、停车和加速出站过程.因此,相邻列车连续经过xa的最小时间间隔Hmin(xa)为

式中:Tin(xa)、Tout(xa)分别为列车进站、出站运行时间;Tdwell为停站时间.
淄博市农村饮水安全工程建设管理现状调查与分析………………………………… 吕晓坤,韩克泉,李 忠(17.17)

图2 车站区域最小追踪间隔Fig.2 Minimum headway of station area
对于任意位置xa,Hmin(xa)取决于Smin(xa)和通过Smin(xa)的列车运行速度.由式(7)~式(9)可知,Smin(xa)取决于v(xa)和xa以前的列车操纵策略有关,通过Smin(xa)的列车运行速度和xa以后的列车操纵策略有关.因此,操纵策略决定了列车追踪运行过程中可实现的最小追踪间隔.全线列车执行相同U在线路上追踪运行,可实现的最小追踪间隔H(U)为列车连续通过最受限制点的最小时间间隔,即
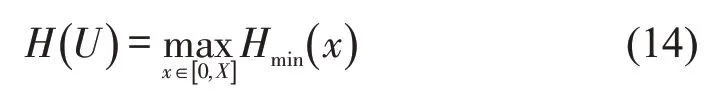
2 列车运行性能优化
2.1 问题描述
列车站间运行时间由运行图预先给定,理论上存在无数种操纵策略保证列车安全、正点运行.面向高峰小时地铁列车密集追踪的运行场景,将其中可实现追踪间隔最小且牵引能耗最小的操纵策略作为最优操纵策略.
Takeuchi[5]对最小追踪间隔计算进行了灵敏度分析,结果表明,增大列车牵引/制动加速度可有效压缩最小追踪间隔.Liu[8]利用极大值原理推导出连续控制条件下的列车节能驾驶最优控制应包括最大牵引、巡航、惰行和最大制动.上述文献表明,列车最大牵引和最大制动是实现节能驾驶和高效追踪的必要控制条件.因此,本文选择最大牵引、巡航、惰行和最大制动组成列车最优操纵策略的4种控制变量,目标问题转化为寻找这些控制变量之间的组合顺序及其对应的转换点.
本文假设列车装备自动驾驶系统,能够在线路任意位置实现巡航控制.因现有地铁系统并未完全装备再生制动设备,为不失一般性,再生制动能不在本文考虑范围内.
2.2 优化模型
将U作为决策变量,将minE(U)和minH(U)作为优化目标,设置列车安全、正点运行约束条件,构建双目标优化模型为

式中:Vlimit(x)为线路限速条件;Tset为指定站间运行时间.
2.3 模型求解
构建双目标优化模型旨在降低列车牵引能耗的同时压缩列车最小追踪间隔,期望得到一组准确的Pareto最优解以体现两目标之间的均衡,采用基于动态规划方法的精确算法求解式(15).由于最小追踪间隔指标在动态规划逐段递推过程中并不严格单调,不具备动态规划方法所需的“无后效性”,引入ε-约束法将其转化为约束条件,并将式(15)转化为单目标优化模型,并以Δε为间隔由小到大调整ε参数值后多次利用动态规划方法进行求解.


图3 模型阶段状态划分示意图Fig.3 Stages and vertices of optimization model
列车在k阶段运行时固定采用最大牵引、巡航、惰行和最大制动中的一种工况,将其简记为uk,列车在相邻阶段的最优控制工况切换还应满足图4所示的接续条件.

图4 列车控制接续约束Fig.4 Train regime switching constraint
列车在k阶段sk,i处施加uk后运行至k+1 阶段(xk+1,v′)处,(xk+1,v′)有可能不属于已划分的开始状态集,需要对其进行近似处理并修正至sk+1,j处,其中,将上述状态转移过程简写为

列车在sk,i处施加uk阶段牵引能耗e(sk,i,uk) 和运行时间t(
sk,i,uk) 计算为

为获取式(16)在ε参数下的最优操纵策略,采用后向动态规划的求解方式,从sK+1,0开始逐段向前推进寻找列车在各阶段的最优控制决策直至s1,0.对于阶段k,将列车从sk,i运行至sK+1,0的操纵子策略记为,其对应的牵引能耗和运行时间分别为和,下面建立评价最优性的过程指标函数.
将列车从s1,0运行至sk,i处的操纵子策略记为,其对应的牵引能耗及运行时间分别记为和因此,式(16)的优化目标minE(U)可拆解为和在后向动态规划求解过程中,无法直接求解得到.列车牵引能耗与运行时间在节能操纵条件下呈反比关系,故等效于因,故等效于因此,评价最优性的过程指标函数为
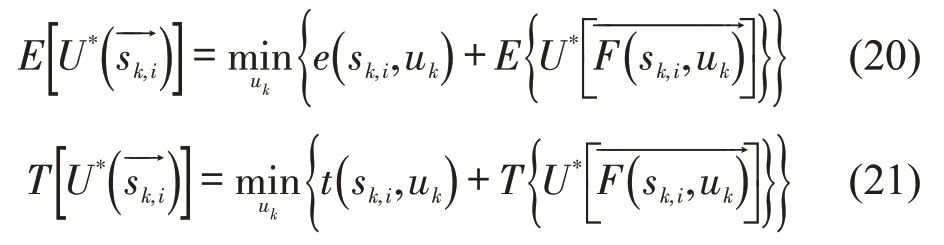
对应的最小追踪间隔应满足ε约束,即

应满足准点运行约束为

特别的,列车在s1,0和sK+1,0的准点约束条件为
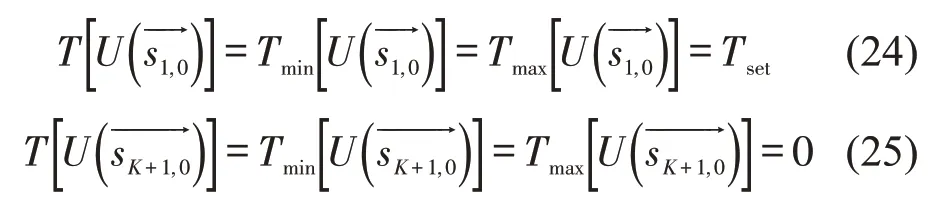
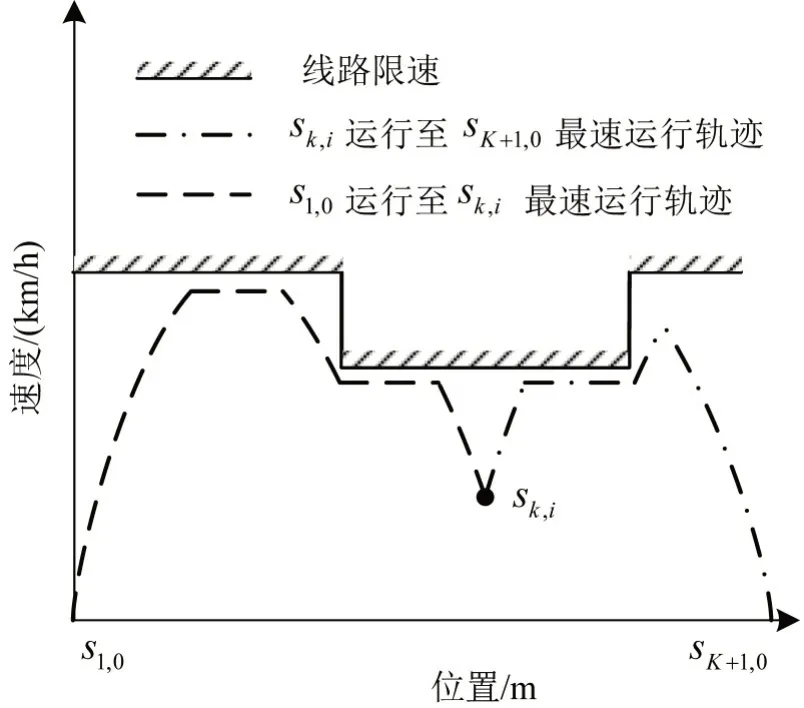
图5 Tmin[U ()]和Tmax[U ()]计算原理Fig.5 Calculation principle of Tmin[U ()]and Tmax[U ()]
由于存在2 个冲突的过程指标,即式(20)和式(21),列车从sk,i处运行至sK+1,0的最优操纵子策略应为一组Pareto解,记为,其中,为sk,i处的第w个最优子策略.动态规划方法从sK+1,0开始逐段向前推进,求解各阶段各状态点的Pareto最优子操纵策略集直至起点s1,0.由于准点运行式(24)的限制,s1,0处的最优操纵策略有且只有一个,为式(16)在ε参数下的最优解,即
式(16)的具体求解步骤描述如下:
Step 1 读入线路数据及列车参数并计算
,设定模型参数Δx、Δv和ε,划分离散状态集合{sk,i},设定边界条件,令k=K,完成模型求解初始化.
Step 2 对于k阶段所有的sk,i,遍历4种最优控制工况uk,获取k+1 阶段F(sk,i,uk)处的最优子策略集在满足式(22)和式(23)的条件下,将uk加入生成sk,i处的可行子策略集
3 算例分析
基于C++开发优化程序,以北京地铁亦庄线为算例,选择文献[2]中线路数据和车辆参数,在此基础上进一步设定,aeb=-1.0 m/s2、Lsm=30 m、Ltrain=90 m、Treact=0.5 s 和Tdwell=30 s.根据“计算时间—优化效益可接受原则”设置模型参数如下:Δx=10 m、Δv=1 km/h 和Δε=0.1,模型参数决定模型的求解精度和求解效率,间隔越小,模型求解精度越高且求解效率越低.以第7 区间“万源街—荣京东”为例:首先,令ε=0,不断迭代计算ε=ε+Δε后的式(16)直至获取第1个有效解,该解即为能够实现理论最小追踪间隔的操纵策略,令εmin=H();其次,将ε设置为一个较大的正值后对式(16)进行求解,所得解即为只考虑节能目标的最优操纵策略,令εmax=H();最后,以Δε为间隔在[εmin,εmax]内由小到大调整ε参数值,多次求解式(16),获得一组Pareto最优解,如图6所示.
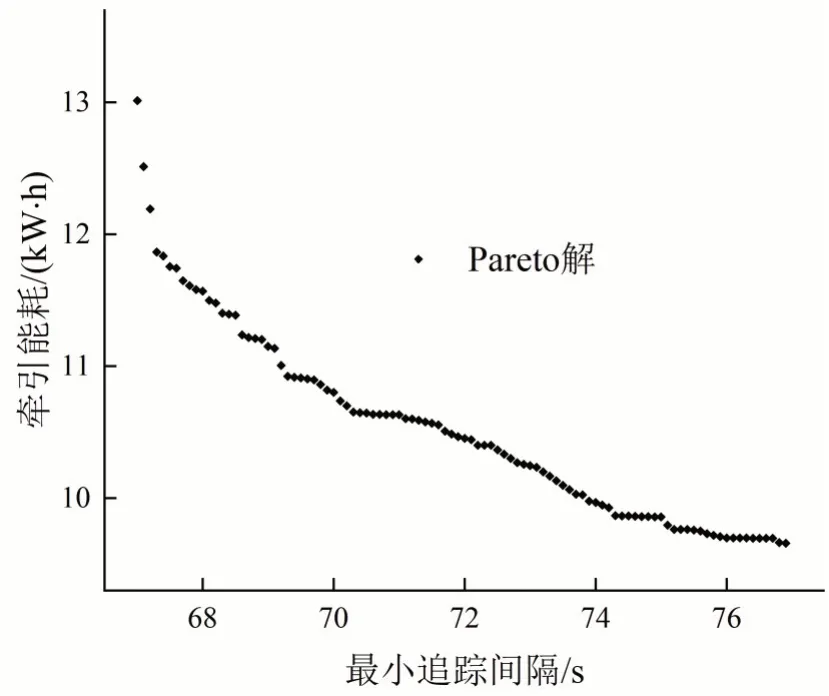
图6 列车最优操纵Pareto 解Fig.6 Pareto solution of optimum driving strategy
选取ε=70 条件下的最优操纵策略,对比、和这3 种策略下的v(x)及其对应的Hmin(x),如图7所示.条件下列车从起点开始最大牵引至A1,然后以惰行和巡航的组合方式运行至B1,最后施加最大制动至终点;列车从C1开始进入车站追踪模式,Hmin(x)发生跃变;的性能指标分别为=9.8 kW⋅h,=77.2 s.条件下列车最大牵引至A2,惰行并巡航至后开始施加第1 次最大制动至C2,然后惰行至B2后施加第2次最大制动至终点;由于提前制动,列车在C2处才进入车站追踪模式,其性能指标为=10.7 kW·h,=70.0 s.同一样,在处提前制动,采用两次制动的进站模式分别经过了A3--C3-B3点,列车自C3开始进入车站追踪模式,性能指标为=13.0 kW·h,=67.1 s.相较于,和在进站过程中执行两次制动策略,压缩了列车最小追踪间隔,为弥补两次制动进站过程中额外消耗的运行时间,和提升了进站以前的运行速度,额外增加了牵引能耗.

图7 、 和 的列车运行轨迹及最小时间间隔Fig.7 Train trajectory and minimum time separation of, and
列车进站操纵策略变化本质上影响的是车站追踪模式下Tin(x)和Tout(x),从而改变Hmin(x).、和策略下的Tin(x)和Tout(x)随v(x)的变化趋势如图8所示.上述操纵策略在车站追踪模式下的运行过程均包含1 次惰行和1 次最大制动.随着列车向终点运行,3 种操纵策略对应的Tout(x)从0开始递增并分别在列车进站的制动初始点B1、B2和B3处达到极大值,Tin(x)呈递减趋势并在终点处减为0.由于不同操纵策略下Tin(x)和Tout(x)存在差异,条件下的Hmin(x)呈先增后减趋势,在B1处达到极大值;和条件下,Hmin(x)分别在C2和C3处达到极大值.

图8 车站追踪模式下列车运行轨迹及相关时间间隔Fig.8 Train trajectory and related time separation under station tracking mode
计算全线13 个站间的最优操纵Pareto 解,选取各站间的与进行比较,如表1所示.与相比,列车在下的全线通行能力提升了17.0%,牵引总能耗增加了19.3%.各站间的均采用两次制动的进站策略且第2次制动的进站初速度都为23.0 km/h,各站间的最小追踪间隔均达到约67 s 的极小值.各站间的都采用一次制动进站策略,其最小追踪间隔的大小与列车进站制动初速度正相关.不失一般性,图9以第2 区间和第4 区间为例,描绘和策略下v(x)和Hmin(x)来进一步印证上述结论.

表1 列车操纵策略优化结果Table 1 Optimaziton results of driving strategy

图9 和的列车运行轨迹及最小时间间隔Fig.9 Train trajectory and minimu time separation of 和
4 结 论
列车操纵策略决定了列车在线路上运行的牵引能耗和可实现的最小追踪间隔.列车采用两次制动的进站策略可以有效压缩最小追踪间隔,但需要消耗更多的牵引能耗.列车最小追踪间隔和进站制动初速度正相关且存在极小值.相较于只考虑节能目标的最优操纵策略,追踪间隔压缩后的最优操纵策略最多可提升17.0%的线路通过能力,同时也增加了19.3%的牵引能耗.运营商可权衡地铁高峰小时服务水平和运营成本的实际需求,利用本文方法获得列车追踪运行最优操纵策略,具有一定实际意义.随着再生制动设备在城市轨道交通系统的应用普及,考虑再生制动能利用的列车运行能耗和追踪间隔多目标优化问题有待进一步讨论.

