光纤光栅三维拉力传感器设计
谢 凯,谭 滔,司学振,吕中宾,任鹏亮,仇成军,段 超,田 野,柴 全,高 菲,张建中
1.国网河南省电力公司电力科学研究院,河南郑州450052
2.哈尔滨工程大学纤维集成教育部重点实验室,黑龙江哈尔滨150001
3.中国船舶工业系统工程研究院,北京100094
在特高压输电网络中,特高压变压器、高压套管和避雷器是整个输电系统的重要组成部分.高压套管是将变压器内部的高压绕组线引到油箱外部,实现与套管外部的高压引下线相连的出线装置,其作用是对高压引线对地绝缘和固定引线;避雷器则用于保护电气设备免受高瞬态过电压危害并限制续流时间和续流幅值[1].高压套管、避雷器一般通过接线端子和引下线与站内跨线进行连接,因此套管顶部与接线端子保持良好接触是维持变电站长期可靠安全运行的前提.由于室外环境复杂,套管端部的接线端子在复杂的风、雨、振动等环境作用下端部受力复杂,常发生变形或与变压器接触不良等情况[2-5],极易导致变电站事故的发生.因此套管监测也是变电站研究的一个重要内容.
对变电站高压套管的研究主要集中在电气性能[6-7]、材料[8-9]和安装[10-12]等方面,而对套管端部的力学性能研究较少.2016年,国家电网提出的《国家电网公司十八项电网重大反事故措施》中明确要求,引流线(包含金具)对套管接线柱的作用力不能大于套管及接线端子的弯曲负荷耐受值,因此保护套管安全、监测套管端部受力逐渐成为变电站健康监测的重要内容.自2017年起河南省电力公司开始对变电站高压套管端部的受力状态进行研究,分析了接线端子连接金具系统[13]和接线端子处的引下线连接方式[14]在风载荷下的力学性能,并采用应变片设计了三维拉力传感器[15-16],实现了对接线端子断电状态下的受力测量.但所设计的应变片三维拉力传感器需用24 个应变片进行三维拉力解调,三维力解调复杂且应变片传感器难以在变压器高压、强电磁环境中进行长时间稳定的实时在线测量.
光纤传感器具有体积小、耐电磁环境干扰、稳定性高、可复用等优点,可代替应变片传感器运用于各个领域[17-19].本文基于光纤光栅传感器设计了可运用于高压套管端部三维拉力监测的光纤型三维拉力测量传感器.通过分析传感器的应变分布得到结构上在3 个方向加载的应变分布规律,并得到了结构上的形变最大位置,确定了三维拉力的解调方法并优化了传感器的布置和解调方法.最终选用5 个光纤光栅应变差传感器和3 个温度传感器组成阵列,对传感器进行温度补偿和三维拉力解调,优化了应变片三维拉力传感器的布置.通过实验加载三维拉力验证了传感器解调三维拉力的准确性.该传感器将用于载电环境中进行实时、长时间、稳定的拉力测量,保证变电站的安全运行.
1 传感原理
本文基于光纤光栅传感器设计三维拉力传感器.光纤光栅的核心部件是刻在光纤芯上的光栅结构,它通常会改变光纤的折射率.纤芯外面是包层,用于保护纤芯结构.当宽带光进入光栅光纤时,波长满足布拉格条件的光将被反射[20],而其他波长将继续向前传播:

式中,λB为布拉格波长;neff为有效折射率;Λ为光栅的空间周期.
如式(1)所示,反射波长取决于光栅的空间周期.当材料经历温度变化或应变时,反射波长将从λB发生漂移[21].反射波长漂移与应变和温度灵敏度关系如下:
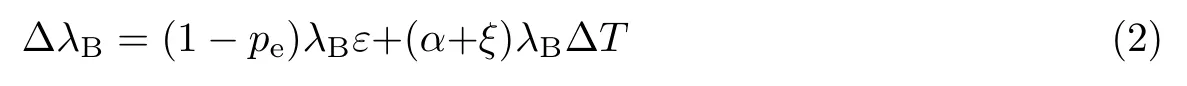
式中,∆λB为布拉格波长的变化;pe为一个常数,取决于应变光学张量和泊松比,通常假设为0.21∼0.22;ε定义为应变;α为热膨胀系数;ξ为光纤折射率的热光系数;∆T为温度变化量.因此在使用光纤光栅作为传感器时需要考虑温度、应力对光纤光栅的影响.
基于光纤光栅传感器三维拉力解调原理公式为
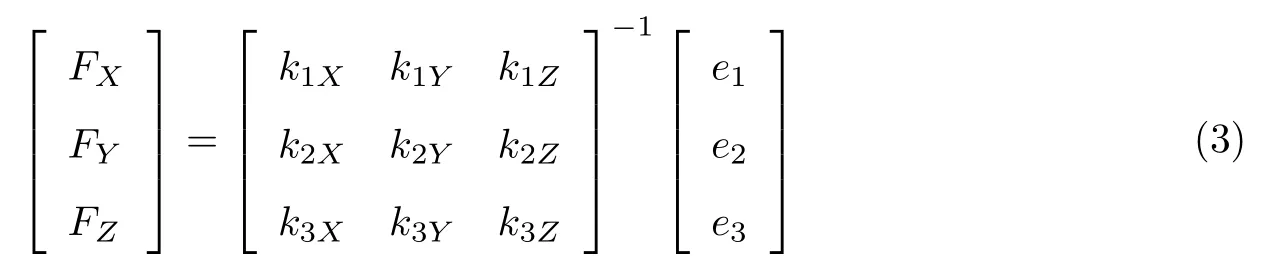
式中,e1、e2、e3分别为光纤光栅传感器组成阵列测量X、Y、Z方向三维拉力的应变,FX、FY、FZ分别为3 个方向的三维拉力;kiX、kiY、kiZ(i=1,2,3)分别为e1、e2、e3在X、Y、Z方向上的灵敏度.通过将光纤光栅阵列测量得到的应变值e1、e2、e3带入式(3),即可求得三维加载力FX、FY、FZ.
2 传感器解调设计
基于光纤光栅设计三维拉力传感器模型结构如图1(a)所示.该模型在整块高强度钢材料上设计呈现对称结构,结构中间向上凸起部分为加载端,结构左右向下凸起部分为固定端,四周为梁.左右固定端有固定的螺纹孔,通过4 个固定端螺纹孔将结构固定在变电站套管架上,中间螺纹孔为受力螺纹孔,安装在接线端子上.梁四周开有上下光纤走线槽,尺寸为宽2.2 mm、深2 mm.图1(b)为传感器封装完成后的传感器实物图,表1为模型结构参数.
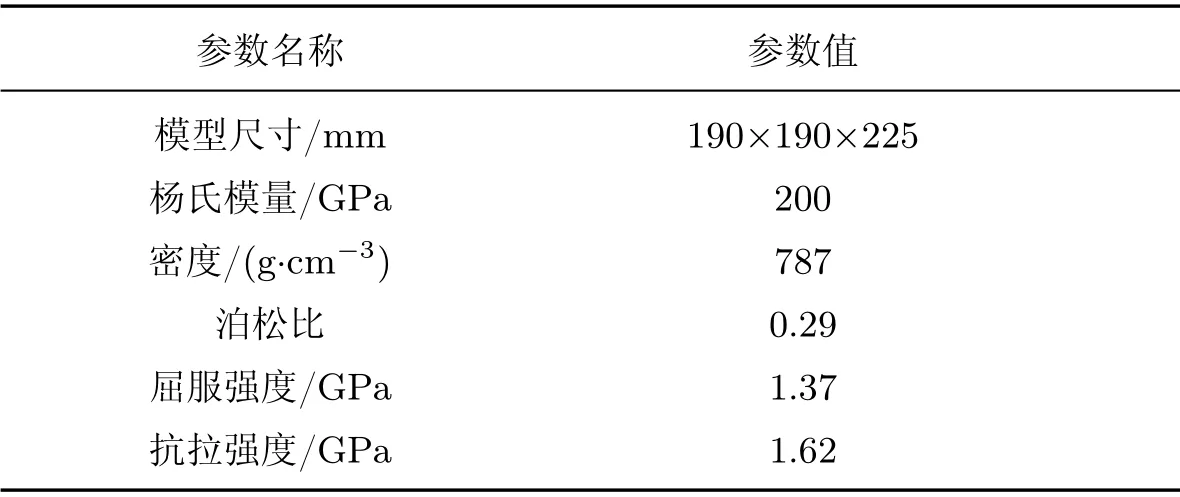
表1 模型结构参数Table 1 Structure model parameters
对传感器结构进行有限元仿真计算,分析结构的变形特点以得到三维拉力的解调方法.在加载端分别沿X、Y、Z方向加载10 000 N 进行计算,得到结构在3 个方向的应变分布,如图2所示.
在X方向加载下结构的3 个方向的应变分布均是关于X轴对称的,在Y方向加载下结构的3 个方向的应变分布均关于Y轴对称,在Z方向加载下结构的3 个方向的应变分布是关于坐标轴轴对称分布的.在3 个方向加载下,四周梁与固定端和加载端连接位置均出现了应变集中,说明这些转折位置易发生较大形变.基于结构在三维拉力加载下的对称性和分析对称性的差异来设计解调方案,考虑到梁上易出现的应变集中位置,这些位置可以作为传感器的布置位置以提高测量信号值.

图2 加载10 000 N 结构应变分布图Figure 2 Strain distribution of structure loaded with 10 000 N
详细分析结构的应变分布,将结构上下槽边缘曲线的应变分布按照图1中面①、②、③、④的顺序依次展开,得到其在各自方向的应变,如图3所示.
图3中横坐标为边长度,纵坐标为曲线上的应变,红色实线为上边缘曲线,蓝色虚线为下边缘曲线.在X和Y方向加载时,上下曲线的应变响应是一致的,但在Z方向加载时上下曲线的应变是相反的,因此通过上下曲线应变的相反规律来解调Z方向的加载.在X方向加载时,①和③面上的曲线响应相反,②和④面上的曲线响应相同,且①和③面上的应变大小要大于②和④面;在Y方向加载时,①和③面上的曲线响应相同,②和④面上的曲线响应相反,且②和④面上的应变大小要大于①和③面.因此根据此规律,采用①和③面上点的应变相减来解调X方向加载的力,②和④面上点的应变相减来解调Y方向加载的力,上下曲线上点的应变相减来解调Z方向加载的力.在各曲线上还出现应变较大的位置,这些位置是传感器结构中梁与固定端和加载端相连接的位置,因此传感器布置的位置选择在这些应变集中的位置可获得更大的测量信号.

图3 加载10 000 N 槽边缘曲线应变分布Figure 3 Strain distribution on the edge of the groove loaded with 10 000 N
基于传感器的应变分布规律、对称性和应变集中位置,选择解调方案,如图4所示.在结构上共布置5 个光纤光栅应变传感器和3 个光纤光栅温度传感器.光栅1 和3 进行X方向力解调,光栅2 和4 进行Y方向力解调,光栅2 和5 进行Z方向力解调.温度传感器T1对光栅1进行温度补偿,T2对光栅2、3、5 进行温度补偿,T3对光栅4 进行温度补偿.温度补偿之后,传感器的解调公式如下:

式中,εi(i=1,2,3,···,5)为各应变光栅测量的应变;T1、T2、T3为温度传感器测量值;KTi(i=1,2,3,···,5)为各应变光栅温度灵敏度;e1、e2、e3分别为传感器解调X、Y、Z方向的应变.基于光纤光栅的复用优势,8 个光纤光栅均在一根光纤上便于解调,且采用8 个传感器进行解调,远低于应变片三维拉力传感器的24 个传感器,优化了应变片三维拉力传感器.
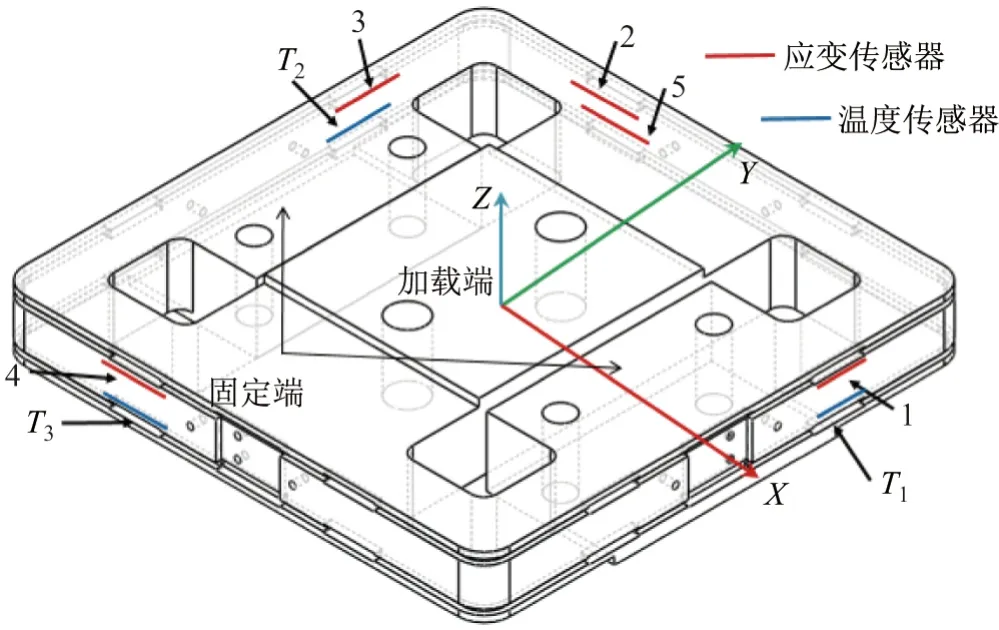
图4 传感器布置Figure 4 Sensors arrangement
3 传感器标定测试
基于图4传感器布置方案进行传感器封装,在结构上布置8 个光纤光栅制作完成光纤光栅三维拉力传感器.采用恒温箱对传感器进行温度标定,标定结果如图5所示,灵敏度如表2所示.
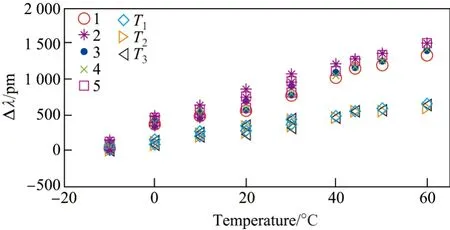
图5 温度标定Figure 5 Temperature calibration

表2 传感器温度灵敏度Table 2 Temperature sensitivity of sensor
传感器中应变光栅1、2、3、4、5 的温度灵敏度基本一致,均在19 pm·◦C−1左右,温度传感器T1、T2、T3的温度灵敏度也基本一致,在9 pm·◦C−1左右.应变光栅的温度灵敏度近乎是温度传感器的2 倍.当传感器处于温度均匀的环境时,即各光栅温度相同,T1=T2=T3,由图4(b)的解调算法可知此时传感器能够进行温度自补偿.当传感器处于温度不均匀环境时,此时温度补偿将会发挥显著作用.
在实验室对传感器进行拉力标定,加载标定示意图如图6(a)所示,各方向实际标定如图6(b)和(c)所示.将传感器固定端固定在光学平台上,加载端与加载设备相连接,标定过程中固定和加载方式均与实际环境的安装一致.标定过程中通过量程为3 000 N 的拉力计对加载的力F进行测量,拉力计精度可达1 N.通过分析加载F与传感器的应变即可得到传感器的灵敏度.

图6 传感器加载Figure 6 Sensor loading
标定过程中传感器在各个方向下重复标定3 次,传感器标定曲线如图7所示.
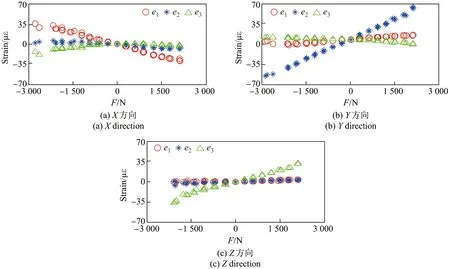
图7 标定曲线Figure 7 Calibration curve
传感器的标定曲线在各个方向下线性度较好.在X方向下e1灵敏度曲线的斜率最大,在Y方向下e2灵敏度曲线的斜率最大,在Z方向下e3灵敏度曲线的斜率最大,说明传感器具有优良的维间耦合误差,解调方案对于三维拉力解调是合理的.在3 次重复标定过程中,灵敏度曲线重复性较好,也说明此结构在三维拉力测量过程中具有良好的重复测量能力.对灵敏度曲线进行拟合得到灵敏度如表3所示,传感器在各个方向的灵敏度为0.01∼0.02 µε·N−1.与仿真结果对比,传感器的灵敏度均小于仿真结果.考虑到实际布置传感器可能产生位置误差,以及实际标定过程中的拉力计读数误差,因此导致传感器的灵敏度小于仿真值是合理的.

表3 三维拉力传感器灵敏度Table 3 Sensitivity of three-dimensional tension sensor
根据仿真结果,模型施加X、Y、Z方向各10 000 N 的力,结构最大的应力为139 MPa,而结构材料的屈服强度为1 370 MPa,因此在10 000 N 变形下,构件仍处于弹性范围内.
通过对解调的三维拉力计算可得到三维拉力的夹角
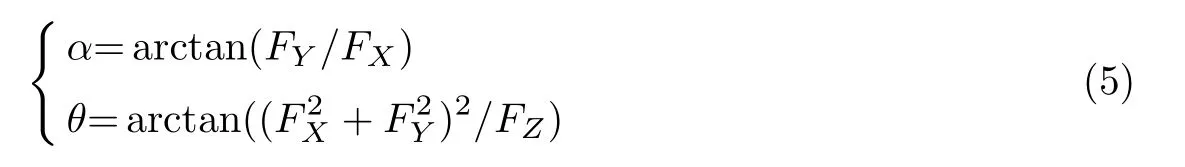
式中,α为合力在XY面投影与X轴的夹角;θ为合力与Z轴的夹角.
对三维拉力传感器灵敏度进行误差分析,在光纤光栅解调中光纤光栅解调分辨率一般为1 pm,即波长的解调误差为1 pm.在此误差下将表2得到灵敏度带入式(3)和(4)中,得到X、Y、Z方向上的三维拉力误差分别为60 N、31 N、84 N.代入式(5),求得α的角度误差为27◦,θ的角度误差为39◦.误差结果在可接受范围内,但仍具有提高空间.
传感器三维拉力加载与解调结果关系如图8所示,图8(a)为加载和解调得到的合力的对比,图8(b)为传感器加载和解调得到的角度的对比.
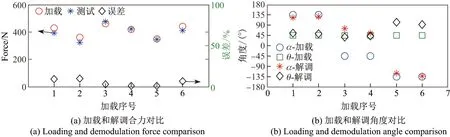
图8 加载解调结果Figure 8 Demodulation results at loading
传感器在加载600 N 范围内的力时,解调得到的力与加载大小基本一致,相差绝对值最大为35.9 N,误差平均值为5.13%.传感器在加载测试中可能存在误差主要有3 个方面:系统解调误差、加载误差、读数误差.产生误差值与分析的解调误差基本一致,说明加载误差是解调误差占主导.传感器解调得到的角度与加载角度基本一致,在传感器3∼4 次加载时,解调角度与加载角度相差较大,在其他测量时角度相差较小.角度的误差在系统解调误差范围内,说明是系统解调误差导致解调角度与加载角度出现偏差.因此系统解调误差对三维拉力解调影响较大,整体而言三维合力和角度误差在可接受范围内,传感器能够实现对三维拉力的准确测量.
4 结 语
本文设计了一种光纤光栅三维拉力传感器,通过有限元仿真分析结构的变形特点,得到了结构解调三维拉力的基本方法,选择在应力集中点布置8 个传感器进行三维拉力的解调.通过实验对设计封装完成的三维拉力传感器进行了温度和拉力灵敏度标定,得到传感器3 个方向的灵敏度在0.01∼0.02 µε·N−1之间.对传感器进行了三维拉力解调验证,传感器的三维拉力大小平均误差为5.13%.因此传感器可实现对三维拉力的准确测量,为变电站变压器高压套管的实时在线监测奠定了基础.

