基于四阶牛顿迭代法的Fast-ICA改进算法

郭松林，徐海鹏

(黑龙江科技大学 电气与控制工程学院， 哈尔滨 150022)

0 引 言

现有的信号分析方法有很多，常用的小波分析法和傅里叶分析法。基于傅里叶变换的信号处理方法由于非周期采样产生泄露误差，使测得的幅值、频率和相角偏离实际值，特别相位测量误差更大。相对于傅里叶变换分析，小波分析具有较大优势，因为小波函数在时域和频域内具有局部分析和多分辨率分析的优势。但由于采样点序列以及所选用的滤波器长度有限，因此，在计算边缘点时会遇到边界问题，随着分解不断进行，重构误差会不断增大。此外，小波分析的运算较复杂，且小波基函数也不易选择，这也是小波分析方法自身的缺点。

独立分量分析方法(ICA)，是近年发展起来的一种有效的盲信号分离方法。该算法可以仅仅根据输入信号的一些基本统计特征，在瞬时混叠参数不清楚的情况下，由观测信号恢复出源信号的过程。通过不断发展和完善的算法理论，使其在语音信号处理、图像处理、无线通信技术、生物医学工程和电气领域等应用十分广泛[1]。而基于牛顿二阶收敛的快速独立分量分析(Fast-ICA)算法，相比于ICA算法收敛速度虽然更快，但依然存在收敛精度和分离性能不高的问题。

笔者为了进一步提高算法的收敛速度和分离性能，减小算法的误差，在原Fast-ICA算法的基础上改进算法，使改进后的算法满足四阶牛顿收敛特性，提升改进后算法的收敛精度与分离性能。

1 盲源分离

1.1 盲源分离原理

典型的盲源分离(BSS)原理[2]如图1所示。

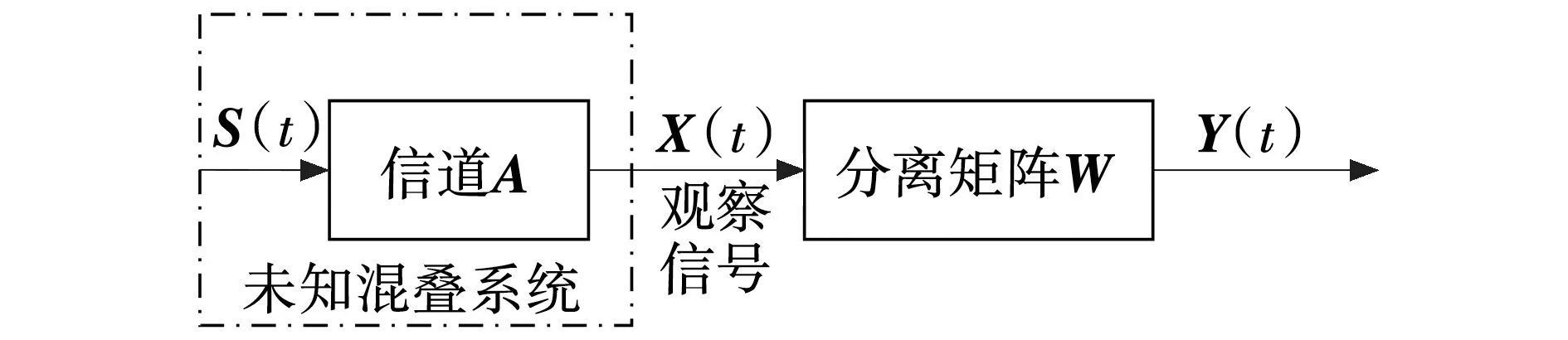
图1 盲源分离原理Fig. 1 Schematic of BSS

n个相互独立的源信号S(t)=[s1(t),s2(t),…，sn(t)]在经过一个未知的混合系统后，得到观测信号X(t)=[x1(t),x2(t),…，xm(t)]，可以近似的表示为

X(t)=A·S(t),

式中：A——m×n维满秩可逆混合矩阵；

X(t)——观测信号；

S(t)——源信号。

当仅知道观测信号X(t)时，可以通过盲源分离优化算法得到分离矩阵，从而得到分离信号为

Y(t)=w·X(t)，

式中：w——m×n维满秩可逆混合矩阵；

Y(t)——分离信号。

Y(t)=[y1(t),y2(t),…，yn(t)]，盲源分离算法就是根据y(t)之间的统计独立性，确定分离矩阵w的过程。为了使盲源分离可以有效地分离，往往需要一些条件来约束，盲源分离最基本的是假设源信号彼此之间是统计独立的，混合矩阵是可逆的，在源信号中高斯信号至多有一个[3]。

1.2 Fast-ICA算法

分离矩阵w是盲源分离以信号的某种独立性为依据确定的。度量信号统计独立性的两个常用指标是峭度和负熵，但峭度容易受到野值的影响，但熵在信息论中是一个较为稳健的判据。随机信号的负熵[4]可以表示为

J(y)=[E{G(y)}-E{G(yg)}]2，

式中：J(y)——负熵；

E{G(y)}——G(y)的数学期望；

y——变量Y的分量；

yg——具有与y同样方差的高斯变量。

如果要分量y的数学期望E{G(yg)}越小，就需要其非高斯性越强，负熵J(y)越大。依据负熵判据寻找矩阵w，使负熵J(y)最大。即对E{G(y)}=E{G(wTx)} 求极值，使最大。因此，导数应为

wT——分离矩阵w的转置矩阵。

g为G的导数，设：xt为t时刻的输入变量X的分量，t+1时刻的输入变量X的分量由牛顿迭代定理可表示为

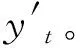
t时刻的算法的输入变量分离矩阵为

式中,wt——t时刻的分离矩阵。

因此，分离矩阵为

2 改进的Fast-ICA算法

不难证明当在原有 Fast-ICA 算法中牛顿迭代算法式是二阶收敛的。由于牛顿算法收敛阶数越高，算法的收敛速度越快，修正原式，使之满足四阶收敛，减小改进后算法的误差并提高收敛速度[5]。其修正形式为

由修正后的牛顿迭代公式，可推得改进 Fast-ICA 算法公式为

改进Fast-ICA算法分由预处理(中心化处理和白化处理)与基于负熵的盲分离算法两部分组成，流程如图2所示。

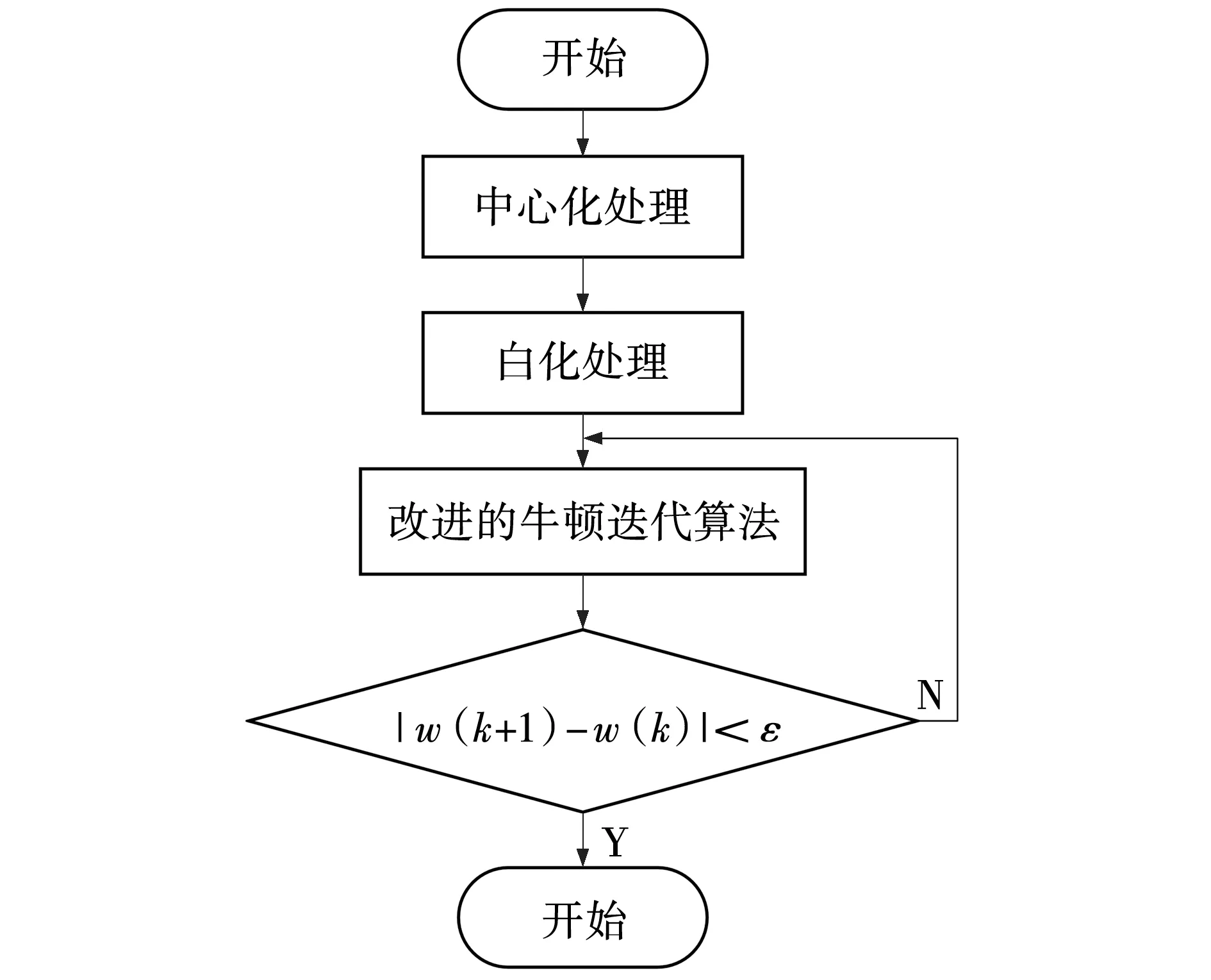
图2 改进算法流程Fig. 2 Improved algorithm flow

2.1 收敛性证明

设f(x)为实数域内四阶可导函数，如果a是f(x)的单根，且x0充分靠近a，则可以根据修正后的牛顿迭代公式定义改进后牛顿迭代误差方程为

证明：设

en=xn-a，

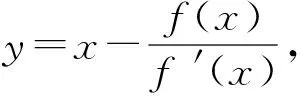
式中：f(a)=0,f′(a)≠0，y(a)=a,

计算得

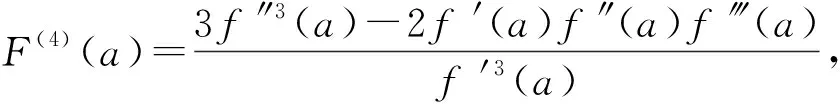
则，迭代公式可以表示为

因此，改进后的Fast-ICA算法是四阶收敛的。

误差方程为

2.2 算法误差的确定

通过以下方法来确定改进后的误差，设

函数表达式为

四阶Fast-ICA算法的最小逼近误差为

假设四阶Fast-ICA误差为10-6>ε>10-7，构建Lyapunov函数为

V(x)=εe-(x-a)，

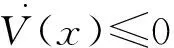
当误差为10-6>ε>10-7时，算法是一定收敛的。对比原算法10-5>ε1>10-6有明显减小[7]。

3 仿真实验与性能

利用Matlab实现Fast-ICA算法对混合信号的分离，为了验证改进算法的有效性，对比分析改进后算法与原算法的仿真结果。

源信号为三路不同的语音信号，利用Matlab将源信号通过随机混合矩阵混合，得到混合信号。三路原始语音信号如图3所示，混合后语音信号如图4所示。

图3 源信号Fig. 3 Source signal

图4 混合信号Fig. 4 Mixed signal

由图4可见，得到混合信号后，分别利用传统的Fast-ICA算法和改进后的Fast-ICA算法分离混合信号。从图5、6可以看出，改进后的算法使语音信号成功分离。

图5 Fast-ICA分离信号Fig. 5 Fast-ICA separation signal

图6 改进的Fast-ICA分离信号Fig. 6 Improved Fast-ICA separation signal

为了比较两种算法实时性，分别对两种算法进行了10次信号分离实验，记录了每次实验两种算法迭代时间，结果如图7所示。原算法和改进后的算法的平均迭代时间分别为0.033 6和0.025 6 s，由图7可以看出，改进后算法的分离时间要比原算法短，即前者提高了收敛效率[8]。

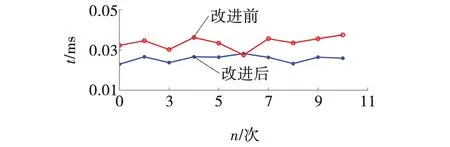
图7 两种算法迭代时间Fig. 7 Iteration time of two algorithms

图8a、b分别是改进后算法的误差图和原算法的误差图。由图8可以看出，改进后的Fast-ICA算法比原来的Fast-ICA在检测精度上有了显著的提高。综上所述，改进后的Fast-ICA算法不仅可以将各个信号有效的分离，而且在实时性和准确性上都要优于原有的Fast-ICA算法[9]。

盲源分离算法的分离性能可以通过算法PI值来衡量[10]，其计算公式为

式中：ePI——算法的PI值;

cij——混合矩阵与分离矩阵的乘积；

m——变量的个数。

如果PI值越小，则说明算法的分离的性能越好，当为零时，证明信号已经完全分离，通过计算，得到改进后算法的PI值为0.52，原算法的PI值为0.66。改进后的算法的值要明显的小于原算法值，由此说明改进后的算法的分离性能要更好。

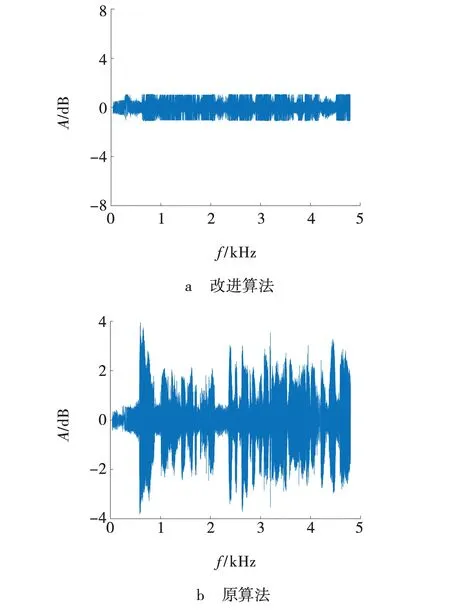
图8 改进算法与原算法的误差对比Fig. 8 Comparing error between improved algorithm and original algorithm

4 结束语

针对原算法收敛速度较慢，收敛精度不高的问题，改进原有算法，使其满足四阶牛顿收敛，证明了其收敛性，确定了改进后算法的误差范围。采用PI值来说明算法的分离性能，最终通过仿真实验证明了文中提出的改进的Fast-ICA算法的代次数和迭代时间均小于原算法，分离信号更接近源信号，分离性能更好。