基于GAPSO算法的NPC逆变器SHEPWM控制方法的优化

沈显庆，马志鹏

(黑龙江科技大学 电气与控制工程学院， 哈尔滨 150022)

0 引 言

PWM调制技术是多电平逆变器中的一项关键技术，与SPWM调制和SVPWM调制相比，SHEPWM调制具有开关频率低、输出波形质量高等优点[1]。在SHEPWM技术中，开关角均由非线性方程组求得，因此，该调制技术的关键在于对建立的方程组进行求解。传统数值方法，如牛顿迭代法[2]、同伦算法[3]、Walsh函数法[4]，原理简单、收敛速度快，但对初值选取依赖性较强，不合适的初值可能会使算法不收敛。目前，研究者们多将智能算法应用于SHEPWM非线性方程组的求解中。王群京等[5]采用标准遗传算法对方程组进行求解，得到不同调制比下的开关角度轨迹，但算法后期容易出现早熟现象。赵义武等[6]利用蚁群算法对目标函数进行优化，求解效果较好，但在算法进化前期由于信息素匮乏会导致求解效率较低。针对上述算法存在的问题，笔者采用一种改进的混合粒子群算法(GAPSO)优化计算SHEPWM的非线性方程组，使开关角度更易收敛于最优解，通过Matlab/Simulink仿真验证该算法求解结果的有效性。

1 NPC逆变器拓扑结构及工作原理

三电平NPC逆变器如图1所示。图中，Ud为直流侧电压；C1、C2为中点电容；D1、D2为箝位二极管；Sa1、Sa2、Sa3、Sa4为开关功率器件。

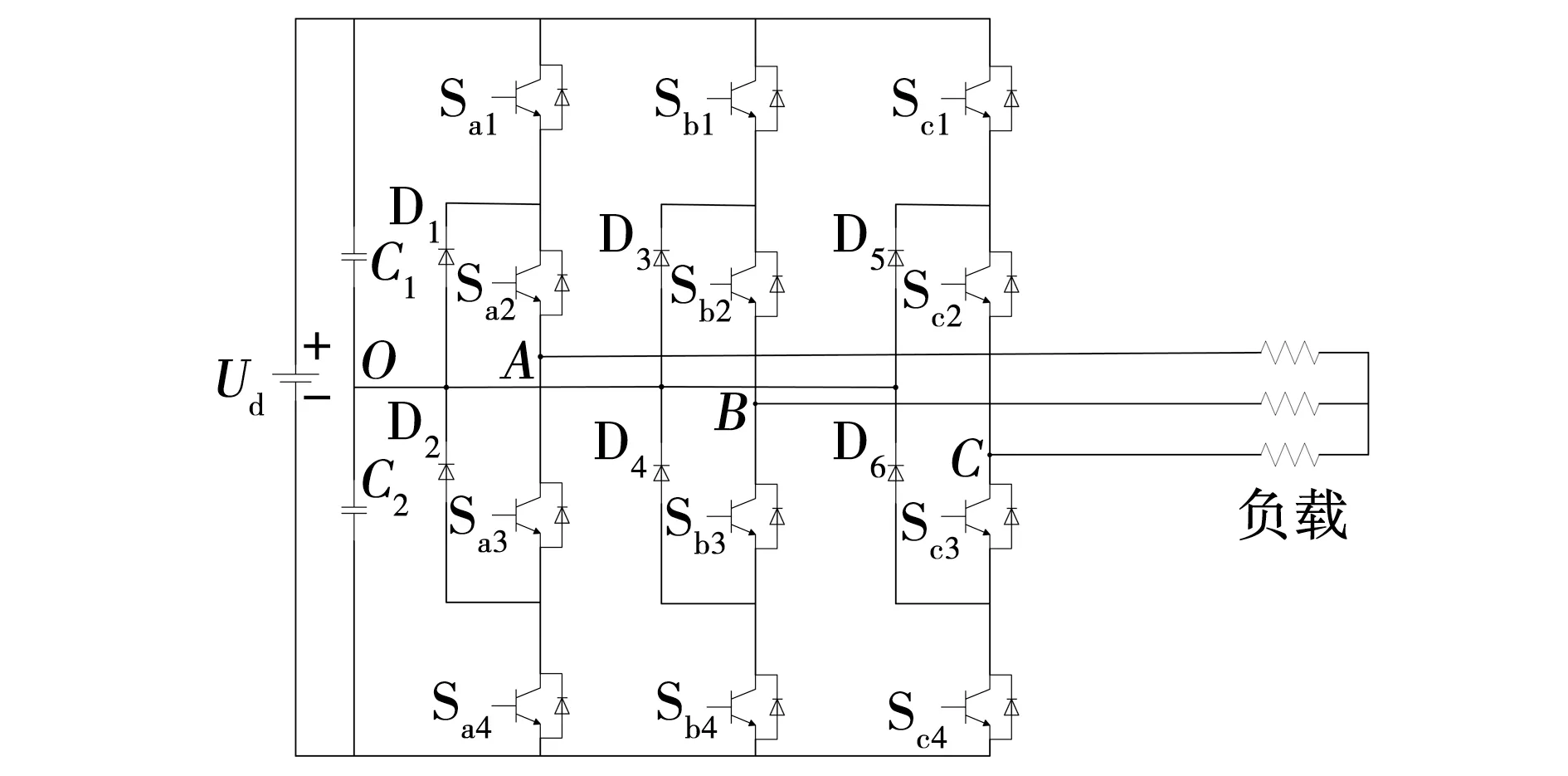
图1 三电平NPC逆变器拓扑结构Fig. 1 Three-level NPC inverter topology

逆变器的每相桥臂由4个开关器件串联而成，具有单个器件所承受的电压低、对开关频率约束小、输出的波形质量好等优点[7]。通过控制相邻的2个开关器件导通或关断，从而得到不同的输出电压。以A相桥臂的4个开关器件为例，定义0为开关器件的截止状态，1为开关器件的导通状态。当Sa1、Sa2为1，Sa3、Sa4为0时，输出电压为Udc/2，称为P状态；当Sa2、Sa3为1，Sa1、Sa4为0时，输出电压为0，称为O状态；当Sa3、Sa4为1，Sa1、Sa2为0时，输出电压为-Udc/2，称为N状态。开关器件导通状态与逆变器输出电压关系如表1所示。

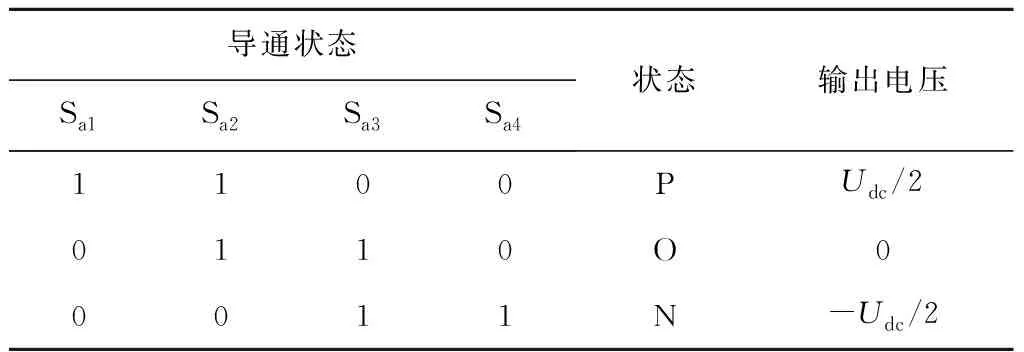
表1 NPC逆变器输出电压及开关器件导通状态

2 三电平SHEPWM方程组的建立

图2为三电平逆变器相电压输出波形，波形满足1/4周期对称，同时考虑到三相系统之间的对称性，线电压中不含有3及3的倍数次谐波，文中只考虑消除5，7，…，6k-1，6k+1次谐波。

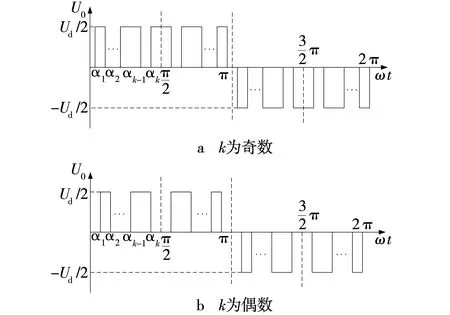
图2 三电平逆变器SHEPWM相电压波形Fig. 2 Phase voltage waveform of 3-level inverter

根据Dirichlet定理，可将相电压波形展开成Fourier级数的形式为

由于相电压波形的奇对称，则有

An=0，

(1)

式中：Umn——n次谐波电压幅值；

n——谐波次数；

N—— 1/4周期内开关角的个数；

Ud——直流侧电压；

ω——基波角频率；

αk——第k个开关角，且开关角应满足条件， 0<α1<α2<…<αN<π/2。

由式(1)可得，只要准确求出开关角的大小就可使Umn=0，即可有选择地消除某些低次谐波。文中以3个开关角为例，主要消除输出电压中的5、7次谐波。令式(1)中的B1=m，B5=0，B7=0，即可在满足基波幅值的情况下，消除目标谐波。建立适应度函数方程为

(2)

式中：Um1——基波电压幅值；

Um5、Um7——5、7次谐波电压幅值；

m——调制比，m=2Um1/Ud。

3 SHEPWM方程组的求解

3.1 PSO算法权重系数的改进

对标准的PSO算法[8]，假设在一个群体中由n个粒子组成，表示为X={x1,x2,…,xn}，每个粒子由一个D维向量xi={xi1,xi2…,xiD}表示。在算法寻优的过程中，粒子通过跟踪个体最优位置和全局最优位置来更新自己，从而在搜索空间中向更好的位置移动，粒子速度及位置更新公式为

式中：t——当前迭代次数；

w——惯性权重；

c1，c2——学习因子；

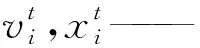
r1，r2——(0,1)之间的随机数；

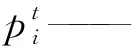
gt——第t次迭代的全局最优位置。

根据SHEPWM方程组的特点，在算法的前中期，惯性权重w应该较大，保证搜索的全局性，在算法迭代寻优的后期，采用数值较小的w值，保证算法在该粒子处搜索的准确性[9]。因此，文中w的取值采用随着迭代次数递减的方式，公式为

式中：wmin、wmax——w的最小值及最大值；

T——最大迭代次数。

3.2 开关角度的求解

在GAPSO算法中[10]，选择操作主要是对种群中的粒子进行一定的筛选，根据适应度函数的值进行排序，从种群中挑选出一些优质个体进行后续迭代。在选择操作的基础上，对这些被挑选出来的粒子以一定的概率pc进行两两交叉，替换种群中的劣质个体，保证种群规模的前后一致。新粒子的位置及速度更新公式为

式中：ε1、ε2——(0,1)之间的随机数；

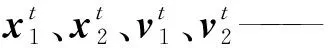
在此基础上，以变异概率pm对种群中的个体一个或多个维数赋以初值，从而避免算法搜索后期种群多样性的丧失。改进的混合粒子群算法(GAPSO)计算步骤如图3所示。

以3个开关角的消谐方程为例，将改进的GAPSO算法用于SHEPWM方程组的求解，将式(2)变换为

cosα1-cosα2+cosα3-πm/4=η1，

cos 5α1-cos 5α2+cos 5α3=η2，

cos 7α1-cos 7α2+cos 7α3=η3。

由此，建立算法的适应度函数：

min:g(α)=|η1|+|η2|+|η3|，

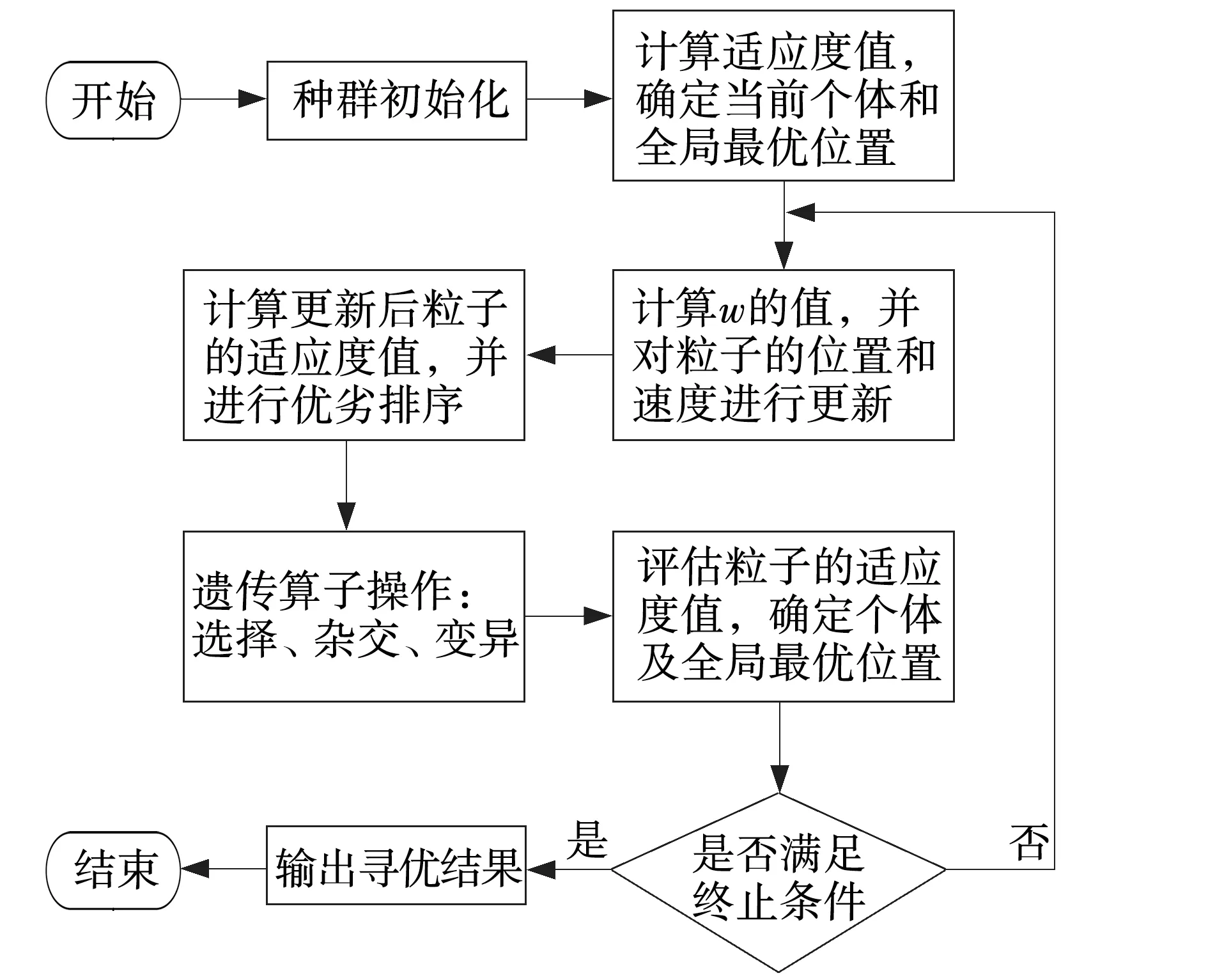
图3 改进的GAPSO算法计算流程Fig. 3 Improved GAPSO algorithm calculation process

经过上述变换，最小多目标问题被转化为一个单目标问题，当g(α)取最小值时，η1、η2、η3均为最小，此时，所求出的开关角度即为方程组的解。

4 系统仿真

改进的GAPSO算法具体参数设置为：粒子群数量n1=200，最大迭代次数T=100，wmin=0.2，wmax=0.7；c1=c2=1.494 45，pc=0.8，pm=0.2。在Matlab 2016a[11]内编写GAPSO角度计算程序，计算得到m=0.7时的三个开关角度为47.856 3°、58.175 2°、66.356 1°及m=0.8时的开关角度为37.072 6°、44.036 8°、56.783 0°。图4为GAPSO算法进化代数与目标函数适应度值的关系，可以明显看出文中所提的改进GAPSO算法收敛速度快，搜寻能力强，在很短的时间内即可计算出最优解，且不容易陷入局部最优。为了验证改进的GAPSO算法求解非线性方程组的有效性，在Matlab/Simulink环境下搭建三电平NPC逆变器仿真系统进行仿真分析。将所计算的开关角度代入仿真模型中，其中直流电压源为2 000 V，输出频率为50 Hz，图5～6为m=0.7时的相、线电压波形及谐波频谱分析，相电压、线电压THD分别为75.75%和47.53%。图7～8为m=0.8时的相、线电压波形及谐波频谱分析,相电压、线电压THD分别为63.64%和41.52%。

图4 适应度进化曲线Fig. 4 Fitness evolution curve

图5 m=0.7时仿真波形Fig. 5 Simulation waveform of m=0.7

图6 m=0.7时仿真频谱Fig. 6 Simulation spectrum of m=0.7

图7 m=0.8时仿真波形Fig. 7 Simulation waveform of m=0.8

图8 m=0.8时仿真频谱Fig. 8 Simulation spectrum of m=0.8

由图5～8可见，逆变器输出的相电压中5、7次谐波含量基本为0，线电压中3的倍数次谐波基本消除，由此证明所提算法计算出开关角度的正确性。

5 结束语

利用GAPSO算法求解了三电平NPC逆变器SHEPWM的非线性方程组，将遗传算法与粒子群算法进行有机融合，克服了传统数值算法对初值要求高、求解精度差及标准PSO算法易早熟等问题，具有搜索时间短，收敛速度快，求解精度高等优点。仿真结果验证了该算法求解SHEPWM方程组的准确性，为SHEPWM方程组的求解提供了一种新的方法。