一种通用摄影测量畸变模型性能仿真分析

孙佳明 余俊鹏 李洁明 满益云 沈刚

一种通用摄影测量畸变模型性能仿真分析

孙佳明1余俊鹏1李洁明1满益云2沈刚1

（1 广东工业大学土木与交通工程学院，广州 510006）（2 钱学森空间技术实验室，北京 100094）

摄影测量中，畸变模型的选择对于保证畸变检校效果十分重要。文章提出了一种基于二元傅里叶级数的通用型畸变模型，理论上可精确拟合各种形式的几何畸变。对模拟畸变数据的拟合试验结果表明，傅里叶模型相比一般多项式模型具有更优的畸变拟合性能，拟合精度随着阶数的增加而稳步提高，对Brown模型畸变拟合中误差可达到0.3像元以内，对Ebner模型畸变拟合中误差达到0.001像元的水平。二元傅里叶模型可在摄影测量数据处理和光学相机检校中替代其他畸变模型，作为一种通用畸变模型使用。

摄影测量 傅里叶级数 畸变模型 仿真分析 航天测绘

0 引言

摄影测量畸变指由于摄影成像系统在视场范围内的成像光束未严格满足理想中心投影而产生的像点位置偏差，反映了镜头光学畸变、感光器件形变、光线折射等因素的综合作用。畸变的检校和补偿对于保证摄影测量精度至关重要[1-4]。

畸变作为一种系统误差，其误差模型大致可分为物理模型和数学模型两大类[5-6]。1965年，美国摄影测量学者Duane C．Brown通过大量试验，对光学相机几何畸变的物理因素深入分析后提出了Brown模型[7]。至今，Brown模型及其改进模型仍是近景和航空摄影测量中被普遍采用的“标准”模型[8-12]。1976年，Ebner提出一种数学模型——正交多项式模型，采用一组正交参数集对摄影测量畸变进行数学拟合，并通过自检校空中三角网光束法平差验证了其有效性[13]。与正交多项式模型类似的数学模型还有一般多项式模型[14]、球面调和函数模型等。

在摄影测量科研和生产实践过程中，不同畸变模型往往根据某种特定情形而提出[15-19]，缺乏较好的通用性。在实际数据处理过程中，很难自动选择最适合的模型进行畸变检校和补偿，从而导致处理结果的精度损失。针对这一问题，本文基于傅里叶级数对连续函数的逼近特性，提出一种可适应任意畸变的通用摄影测量畸变模型，通过仿真试验表明，其畸变拟合性能随着选用阶数增加而提高，可望应用于航天航空遥感影像的高精度几何处理。

1 目标模型

1.1 摄影测量畸变

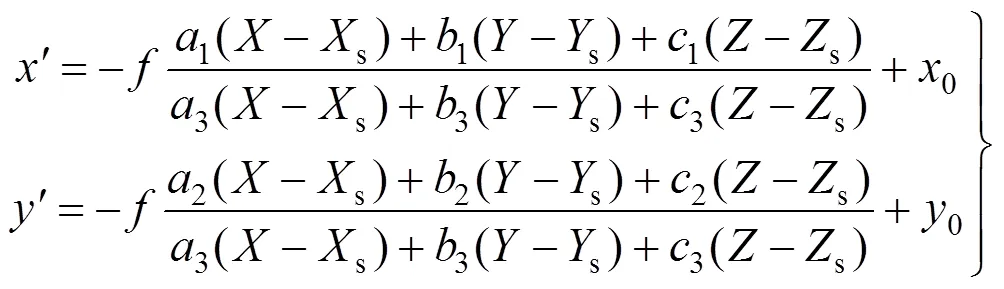
式中1、2分别为、方向的畸变函数。

式（3）中函数关系可有多种选择方案，以下分别给出Brown模型和Ebner模型两种代表性模型。

1.2 Brown模型

Brown模型是一种模拟物理因素作用的经典畸变模型[24]，形式如下：

1.3 Ebner模型

Ebner模型为一种数学畸变模型。在传统摄影测量的9个标准点位上，将畸变量表示为

式中1~12表示、方向的缩放、旋转、错切、弯曲等基本几何形变项的系数；为标准点位距。各项具体形式可参考文献[23]。在传统摄影测量的9个标准点位上，各项参数之间具备正交性，有利于提高求解稳定性和进行参数显著性检验。然而，随着各种数字传感器的应用，像方不规则点位分布情况十分普遍，Ebner模型的适用性有所下降。

2 通用畸变模型

数学畸变模型不必考虑参数的物理意义，适合作为通用型畸变模型使用。一般多项式模型是目前较为常用的通用模型，其形式为：

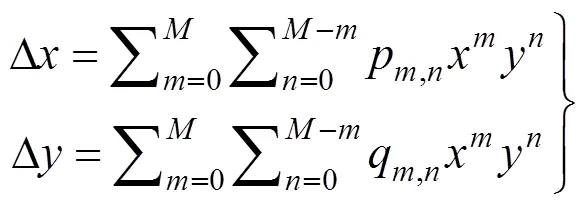
式中为多项式阶数；、分别为各项中、的幂次数；p,n，q,n为多项式各项对应的系数。

随着一般多项式阶数的增加，可以提升其对于特定目标函数的拟合精度，但提升幅度有限，无法实现任意程度逼近。此外实际应用中也不宜过大（一般不超过3），否则容易出现参数过多化而难以求解。因此，寻求一种能够精确拟合各种几何畸变并且便于求解的通用模型，仍然十分必要。

以上各项系数之间严格正交，有利于实现精确求解。以式（7）为基础，得到用二元傅里叶级数逼近像方未知几何畸变的形式，即以像点坐标表示的二元傅里叶畸变模型

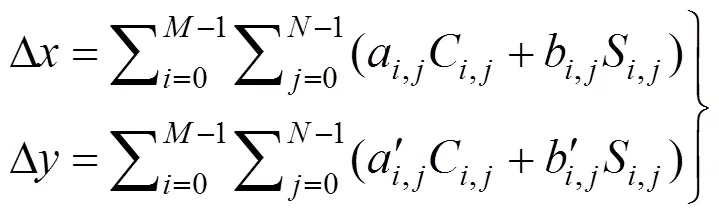
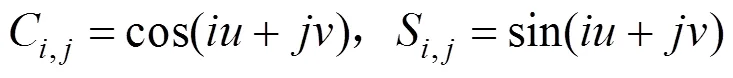
二元傅里叶多项式的阶数越高，对畸变的拟合精度越高。当=1时，傅里叶畸变模型简化为常差模型：

当=2时，式（8）所确定的傅里叶畸变模型含16个待求参数，具体形式为

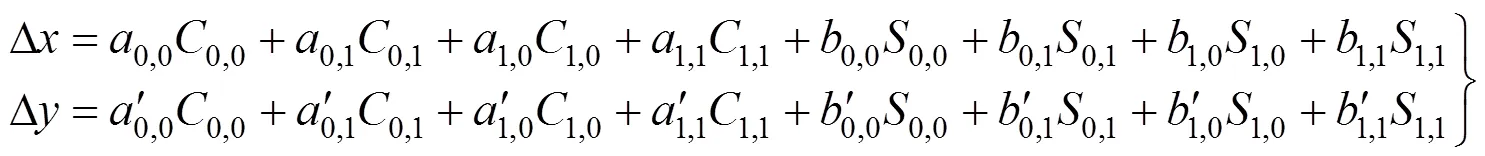
当=3时，畸变模型待求参数增加至36个，形式为

3 试验及结果分析

3.1 试验方法

基于上述理论，可通过仿真试验方法对傅里叶畸变模型的性能进行验证。试验流程如图1所示。首先，在10 000像元×10 000像元的影像范围内，分别以Brown模型和Ebner模型作为目标模型，生成20×20=400个规则格网点位上的模拟畸变值；将各个格网点位坐标与其畸变相加得到模拟像点坐标观测值；然后，以各个点位的模拟畸变值作为观测值，将模拟像点坐标观测值代入式（8），建立观测方程组；按最小二乘原理构造法方程求解参数，统计各点位残差，得到傅里叶模型对目标模型的拟合精度结果。

图1 试验方法流程

3.2 试验结果

3.2.1 对Brown模型的拟合结果

对由Brown模型生成的不同大小畸变，分别用3~7阶傅里叶模型进行拟合，结果见表1。

对不同大小的Brown模型畸变，分别用3阶一般多项式模型和3阶傅里叶模型进行拟合。结果如图2所示。当边缘畸变大小为20像元时，一般多项式拟合中误差大于1个像元，而傅里叶模型拟合中误差为0.8像元。

表1 对Brown模型拟合结果

Tab.1 The fitting results to the Brown model 单位：像元

图2 对Brown模型畸变拟合精度对比

3.2.2 对Ebner模型的拟合结果

对由Ebner模型生成的不同大小畸变，用3~7阶傅里叶模型分别拟合，结果见表2。

对由Ebner模型生成的边缘畸变大小为20像元的情况，畸变拟合前后残差分布如图3所示。可以看出，经拟合后畸变的误差系统性基本消除，拟合效果良好。

3.3 试验分析

试验结果表明，对于Brown模型畸变，当边缘畸变大小分别为5、10、20像元时，采用3阶傅里叶模型拟合，中误差分别为0.2、0.4、0.8个像元，均优于1个像元。采用7阶傅里叶模型，拟合中误差减小到0.1个像元以内，最大残差0.89像元。对比傅里叶模型和一般多项式模型的拟合效果，两者在采用相同阶数时傅里叶模型的拟合精度更优，且畸变较大时精度优势更加明显。

对于Ebner模型畸变，当边缘畸变大小分别为5、10、20像元时，3阶傅里叶模型的拟合中误差分别为0.07、0.14、0.23个像元，均优于0.3个像元，且在行列方向上的残差及中误差大小基本一致。采用7阶傅里叶模型，拟合中误差已达到0.001个像元的水平。

从试验结果可以看出，无论对于Brown模型还是Ebner模型，傅里叶模型的拟合精度都随着阶数增加而不断提高，与其理论特性相符合。

表2 对Ebner模型拟合结果

Tab.2 Fitting results to the Ebner model 单位：像元

图3 对Ebner模型残差拟合前后对比

4 结束语

在摄影测量处理中，由于模拟物理因素作用的畸变模型形式趋于复杂，模型参数与摄影测量定向参数的强相关性导致其解算困难。本文提出一种基于二元傅里叶多项式的数学畸变模型，通过仿真拟合试验表明，3阶傅里叶模型对Brown模型的拟合精度小于1个像元，7阶模型的拟合精度可小于0.1个像元；7阶傅里叶模型对Ebner模型的拟合精度能够达到千分之一像元的水平。在相同阶数情况下，傅里叶模型对畸变拟合效果明显优于一般多项式通用模型。当选取足够高的阶数时，二元傅里叶函数理论上可以任意精度逼近多种畸变函数形式，是一种较为理想的通用模型。后续将开展傅里叶畸变模型在光学相机检校、航空航天摄影测量数据处理等方面的实验研究，进一步考察其实用性能。

[1] 汪佳丽, 王炜杰, 马振玲. 相机畸变的混合模型迭代检校法[J]. 测绘通报, 2019(4): 111-114.WANG Jiali,WANG Weijie, MA Zhenling. Hybrid-model Based Camera Distortion Iterative Calibration Method[J]. Bulletin of Surveying and Mapping, 2019(4): 111-114. (in Chinese)

[2] 崔璨璨, 汪佳丽, 马振玲. 相机检校的迭代处理方法[J]. 测绘通报, 2018(6): 50-54, 60.CUI Cancan, WANG Jiali, MA Zhenling. The Iterative Method of Camera Calibration[J]. Bulletin of Surveying and Mapping, 2018(6): 50-54, 60. (in Chinese)

[3] 徐文, 龙小祥, 李庆鹏, 等. “高分四号”卫星影像辐射与几何精度评价[J]. 航天返回与遥感, 2016, 37(4): 16-25.XU Wen, LONG Xiaoxiang, LI Qingpeng, et al. Image Radiometric and Geometric Accuracy Evaluation of GF-4 Satellite[J]. Spacecraft Recovery & Remote Sensing, 2016, 37(4): 16-25. (in Chinese)

[4] 朱瑶, 王治乐, 贺磊, 等. 线扫描相机标定及畸变矫正方法[J]. 航天返回与遥感, 2017, 38(6): 46-53.ZHU Yao, WANG Zhile, HE Lei, et al. Calibration and Distortion Correction Method of Line Scan Camera[J]. Spacecraft Recovery & Remote Sensing, 2017, 38(6): 46-53. (in Chinese)

[5] 黄留波. 不同畸变模型在航摄相机校准中的适用性研究[J]. 广西水利水电, 2016(4): 24-27. HUANG Liubo. Study of Adaptability of Different Distortion Model in Aerial Photographic Camera Calibration[J]. Guangxi Water Resources & Hydropower Engineering, 2016(4): 24-27. (in Chinese)

[6] 陈国平. 摄影测量与遥感[M]. 武汉: 武汉大学出版社, 2011. CHEN Guoping. Photogrammetry and Remote Sensing[M]. Wuhan: Wuhan University Press, 2011. (in Chinese)

[7] BROWN D C. Close-range Camera Calibration[J]. Photogrammetric Engineering, 1971, 37(8): 855-866.

[8] 杨韫澜, 韩玲, 胡海彦. Brown自检校模型相关性分析与改进[J]. 测绘通报, 2014(5): 37-40.YANG Yunlan, HAN Ling, HU Haiyan. Correlation Analysis and Improvement of Brown Self-calibration Model[J]. Bulletin of Surveying and Mapping, 2014(5): 37-40. (in Chinese)

[9] 孙鹏. 大尺寸动态摄影测量关键技术研究[D]. 北京: 北京邮电大学, 2019. SUN Peng. Research on Key Techniques of Large Scale Dynamic Photogrammetry[D]. Beijing: Beijing University of Posts and Telecommunications, 2019. (in Chinese)

[10] 曹宗伟, 李星全, 杜沛远. 数字摄影测量相机的畸变测量与纠正[J]. 测绘工程, 2017, 26(3): 60-64. CAO Zongwei, LI Xingquan, DU Peiyuan. Distortion Measurement and Correction of Digital Photogrammetry Camera[J]. Engineering of Surveying and Mapping , 2017, 26(3): 60-64. (in Chinese)

[11] 冯其强. 数字工业摄影测量技术研究与实践[D]. 郑州: 解放军信息工程大学, 2010. FENG Qiqiang. Research and Practice of Digital Industrial Photogrammetry[D]. Zhengzhou: PLA Information Engineering University, 2010. (in Chinese)

[12] 冯文灏, 商浩亮, 侯文广. 影像的数字畸变模型[J]. 武汉大学学报(信息科学版), 2006, 31(2): 99-103. FENG Wenhao, SHANG Haoliang, HOU Wenguang. A Digital Distortion Model for all Kinds of Imaging Systems[J]. Geomatics and Information Science of Wuhan University, 2006, 31(2): 99-103. (in Chinese)

[13] EBNER H. Self-calibrating Block Adjustment[J]. Bildmessung and Luftbildwesen, 1976, 44(4): 128-139.

[14] 杨韫澜. 摄影测量自检校技术研究[D]. 西安: 长安大学, 2015. YANG Yunlan. Study on the Self-calibration Technology in Photogrammetry[D]. Xi'an: Chang'an University, 2015. (in Chinese)

[15] 刘世杰, 唐新明, 王凤香, 等. 基于遥感影像的卫星颤振探测分析的关键技术与实现[J]. 地球信息科学学报, 2015, 17(6): 724-731. LIU Shijie, TANG Xinming, WANG Fengxiang, et al. Research on Key Technology and Implementation of Detection and Analysis of Satellite Attitude Jitter Using Remote Sensing Imagery[J]. Journal of Geo-Information Science, 2015, 17(6): 724-731. (in Chinese)

[16] 童小华, 叶真, 刘世杰. 高分辨率卫星颤振探测补偿的关键技术方法与应用[J]. 测绘学报, 2017, 46(10): 1500-1508. TONG Xiaohua, YE Zhen, LIU Shijie. Essential Technology and Application of Jitter Detection and Compensation for High Resolution Satellites[J].Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1500-1508. (in Chinese)

[17] 胡堃, 黄旭, 张永军, 等. 基于高频角位移数据的卫星平台颤振检测与影像几何质量补偿[J]. 电子与信息学报, 2018, 40(7): 6-12. HU Kun, HUANG Xu, ZHANG Yongjun, et al. Satellite Platform Jitter Detection and Image Geometric Quality Compensation Based on High-frequency Angular Displacement Data[J]. Journal of Electronics and Information Technology, 2018, 40(7): 6-12. (in Chinese)

[18] 张宏伟, 张炳先, 侯作勋, 等. 顾及光行差改正的遥感卫星成像模型及验证[J]. 航天返回与遥感, 2019, 40(4): 112-121. ZHANG Hongwei, ZHANG Bingxian, HOU Zuoxun, et al. Construction and Verification of Imaging Model for Optical Remote Sensing Satellite Considering the Correction of Aberration of Light[J]. Spacecraft Recovery & Remote Sensing, 2019, 40(4): 112-121. (in Chinese)

[19] 王密, 朱映, 范城城. 高分辨率光学卫星影像平台震颤几何精度影响分析与处理研究综述[J]. 武汉大学学报(信息科学版), 2018, 43(12): 146-155. WANG Mi, ZHU Ying, FAN Chengcheng.Development of Platform Jitter Geometric Analysis and Processing for High-Resolution Optical Satellite Imagery[J]. Journal of Wuhan University (Information Science Edition), 2018, 43(12): 146-155. (in Chinese)

[20] 余俊鹏, 何炽荣. GPS-RTK辅助近景摄影测量光束法平差及精度分析[J]. 广东工业大学学报, 2017, 34(6): 73-77. YU Junpeng, HE Chirong. An Accuracy Analysis of GPS-RTK Assisted Close-Range Photogrammetric Bundle Adjustment[J]. Journal of Guangdong University of Technology, 2017, 34(6): 73-77. (in Chinese)

[21] 姚娜, 林招荣, 任超锋, 等. 一种适合摄像机非线性畸变校正的畸变模型[J]. 激光与光电子学进展, 2014, 51(2): 167-174. YAO Na, LIN Zhaorong, REN Chaofeng, et al. A Distortion Model Suitable for Nonlinear Distortion Correction of Digital Video Camera[J]. Laser & Optoelectronics Progress, 2014, 51(2): 167-174. (in Chinese)

[22] 蒋永华, 张过, 唐新明, 等. 资源三号测绘卫星三线阵影像高精度几何检校[J]. 测绘学报, 2013, 42(4): 523-529, 553.JIANG Yonghua, ZHANG Guo, TANG Xinming, et al. High Accuracy Geometric Calibration of ZY-3 Three-line Image[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 523-529,553. (in Chinese)

[23] 李德仁, 袁修孝. 误差处理与可靠性理论[M]. 2版. 武汉: 武汉大学出版社, 2012. LI Deren, YUAN Xiuxiao. Error Processing and Reliability Theory[M]. 2nd ed. Wuhan: Wuhan University Press, 2012. (in Chinese)

[24] 高瞻宇. 采用简化Brown模型及改进BFGS法的相机自标定[J]. 光学精密工程, 2017, 25(9): 2532-2540. GAO Zhanyu. Self-calibration Based on Simplified Brown Non-linear Camera Model and Modified BFGS Algorithm[J]. Optics and Precision Engineering, 2017, 25(9): 2532-2540. (in Chinese)

[25] TANG R, FRITSCH D, CRAMER M. New Rigorous and Flexible Fourier Self-calibration Models for Airborne Camera Calibration[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2012, 71: 76-85.

Performance Analysis of a Generic Photogrammetric Distortion Model

SUN Jiaming1YU Junpeng1LI Jieming1MAN Yiyun2SHEN Gang1

（1 School of Civil and Traffic Engineering, Guangdong University of Technology, Guangzhou 510006, China）（2 Qian Xuesen Laboratory of Space Technology, Beijing 100094, China）

The selection of distortion models in photogrammetry is very important to ensure distortion calibration effect. In this paper, a generic distortion model based on binary Fourier series is proposed, which can approximate various forms of geometric distortion with high precision theoretically. The fitting test results on simulated distortion data show that the Fourier model has better distortion fitting performance than the general polynomial model, the fitting accuracy steadily improves with the increase of the order, and the fitting error to the Brown distortion can reach within 0.3 pixel, the fitting error to the Ebner model reaches the level of 0.001 pixel. The binary Fourier model is expected to replace other distortion models in photogrammetric data processing and optical camera calibration as a generic distortion model.

photogrammetry; Fourier series; distortion model; simulation analysis; space mapping

P237

A

1009-8518(2020)05-0110-08

10.3969/j.issn.1009-8518.2020.05.013

2019-12-12

国家自然科学基金青年基金项目（41704019）

孙佳明, 余俊鹏, 李洁明, 等. 一种通用摄影测量畸变模型性能仿真分析[J]. 航天返回与遥感, 2020, 41(5): 110-117.

SUN Jiaming, YU Junpeng, LI Jieming, et al. Performance Analysis of a Generic Photogrammetric Distortion Model[J]. Spacecraft Recovery & Remote Sensing, 2020, 41(5): 110-117. (in Chinese)

孙佳明，男，1995年生，广东工业大学测绘科学与技术专业在读硕士研究生，主要研究方向为摄影测量与遥感。E-mail：1164783700@qq.com。

余俊鹏，男，1982年生，2009年获武汉大学摄影测量与遥感专业博士学位，高级工程师。主要研究方向为摄影测量与遥感。E-mail：strength701@163.com。

（编辑：夏淑密）