离子束加工中全频段误差的演变

李文卿 张继友 王永刚 马仙梅 孟晓辉 李昂

离子束加工中全频段误差的演变

李文卿1,2张继友1,2王永刚1,2马仙梅1孟晓辉1,2李昂1,2

（1 北京空间机电研究所，北京 100094）（2 国防科技工业光学超精密加工技术创新中心，北京 100094）

在空间光学、光刻物镜、惯性约束聚变及强光系统等领域的高精密光学元件制造过程中，采用基于小磨头抛光原理的修形技术，虽然能有效去除面形低频误差，但对中高频误差难以修正。为了达到有效控制全频段误差的目的，文章以直径420mm的非球面为样件，在离子束抛光机床上进行不同频段误差的修形收敛试验。针对光学元件面形误差在不同频段的特性，以面形误差频段均方根及梯度均方根指标作为评价参数，分析各频段误差产生的原因，探索离子束工艺参数及其他因素与各频段误差间的对应关系。通过4轮离子束迭代加工后，样件全频段面形误差均方根值从34.973nm收敛到6.025nm，梯度均方根值由0.091/cm收敛到0.061/cm（=632.8nm）。试验结果表明：通过优化离子束的工艺参数，可显著提升光学元件的全频段面形精度，实现频段误差在不同评价参数下的同步收敛。频段均方根及梯度均方根指标可作为评价全频段面形误差变化的标准，对光学加工具有参考价值。

空间频段 全频段误差 离子束修形 工艺参数 航天遥感

0 引言

随着现代光学技术的发展，全频段误差控制已成为高精度光学零件制造的一个基本要求。在空间光学领域，反射镜采用轻量化的结构设计，除了光学加工工艺带来的面形误差之外，镜面还容易产生网格化的镜面误差（即“格子效应”），这是中频误差的一个重要来源[1-2]。不同频段的制造误差会对光学性能产生不同的影响。一般来说，低频误差使成像系统的像扭曲变形，引入各种像差；中频误差使光线发生小角度散射，影响像的对比度；高频误差使光线发生大角度散射，降低镜面的反射率[3-4]。基于小磨头抛光原理的先进修形技术，虽然能有效修正低频面形误差，但对于中高频段的面形误差难以有效修正。中高频误差成为了现代光学加工普遍关注的难点。而离子束加工的确定性、非接触性以及去除函数可调节性却为高精度光学零件的全频段误差收敛提供了最大的可能性[5-7]。关于离子束加工，国外早已开展了深入研究，如：德国IOM、NTG、卡尔蔡司（CarlZeiss）等公司，日本东京理科大学等研究机构，均具备了十分成熟的设备和工艺。国内离子束技术虽然起步较晚，但目前也逐步由实验室研究阶段转化为工程实践应用，如：中科院长春光机所、中科院光电技术研究所。均通过离子束加工技术得到了高精度的光学元件；国防科技大学也自主研发了离子束抛光设备，经过近年来的研究和改进，其面形收敛效率也逐步接近国际水平[8-10]。本文涉及的试验使用的设备及工艺方法，在米级非球面光学元件加工效率上已经得到验证，具备研究全频段误差控制的基础条件。

要做到全频段误差的高效收敛，除了具备高性能的加工设备以外，还需要能够精确指导光学加工的面形输入，这就对频段误差的分布评价指标提出了更高的要求。目前，功率谱密度PSD（Power Spectrum Density）指标在评价频段误差中得到行业内比较广泛的认可[10-12]。PSD能准确的反映不同频段误差的幅值信息，但由于缺乏相位信息，不能与光学元件的被检波前形成唯一的对应关系，即不同的被检波前可以具有相同的PSD，这就导致当光学元件某一频率的PSD没有达到指标时，理论上存在着无数种加工方案，不能给出一个确定性的加工依据，对于光学加工的指导意义不大。同时，PSD对一些局部的数据，尤其是边缘点数据尤为敏感，即使波前误差评价参数稳定收敛，但PSD曲线在加工过程中并不总随着光学性能或者其他指标参数的逐步改善而改善，甚至在某些频段会出现曲线突变的现象[13-15]。因此，本文提出以频段均方根（Root Mean Square，RMS）及梯度均方根（Gradient Root Mean Square，GRMS）指标作为评价参数对表面误差进行表征，并以此为基础，在直径420mm的非球面样件上进行离子束加工试验，在样件全频段误差得到收敛的同时，得到了离子源加工工艺参数与频段误差变化的对应关系。

试验证明，RMS与GRMS指标是更合理的面形误差评价参数，对于光学加工更具指导意义，结合离子束精修技术，可有效修正反射镜的全频段误差。

1 镜面面形频段误差表征参数

1.1 面形频段误差评价参数

作为比PV值更能全面反映波前品质的参数，被检波前（或镜面）范围内与最佳匹配的参考波前的光程差平方和的均方根RMS值[16-18]，对光学加工最具指导意义，其单位为nm。将面形频段误差的均方根值定义为RMS，用数学表达式描述为

式中W为第频段的面形波像差；为采样数。

1.2 面形梯度误差评价参数

数字化干涉仪出现以前光学检测大多采用刀口检测。刀口检测实质上是一种对波前梯度的检测，直接依据波前误差梯度分布对光学加工进行指导。现今在精抛光阶段的光学检测，数字干涉仪占有主导地位，可以对检测给出的波前误差进行微分，得到波前梯度均方根GRMS值指导光学加工，单位为/cm。其中为光学元件的工作波长，在本文研究的可见光区域中为632.8nm。梯度一般表示矢量场沿某一个方向上的变化，在面形检测中为波前相位函数在干涉仪CCD采样坐标系，方向上的变化率，可以直观地表示出光束的聚焦性能与波前分布的关系[19-20]，将波前梯度的均方根值定义为GRMS，数学表达为

式中（,）为一个波前的梯度变化函数。

2 镜面频段误差控制离子束抛光工艺试验

2.1 离子束加工设备

试验使用的设备具有三轴位移系统，加工时离子源以栅线方式扫描加工，工件无需旋转，可将光学零件精抛至纳米级面形精度。离子源的去除函数为近高斯分布，非常适用于面形误差高效率收敛与高精度面形的同步实现[21-23]。加工时，镜面朝下水平放置，离子源垂直指向工件，如图1所示。

图1 离子束加工设备及离子源配置方式

2.2 试验样件及初始面形

直径420mm非球面样件采用了高轻量化率的设计方案，在使用离子束加工之前，已经用沥青小磨头进行了抛光。反射镜表面除了加工残差外，面形误差中还包括小磨头抛光产生的“格子效应”、加工路径误差等。根据式（1）、式（2），对干涉检测获得的数据按空间频段划分成不同频段，获取不同频段的面形频段RMS和GRMS值。

需要指出的是，在光学加工和检测中，通常按空间波段，即空间频段的倒数对面形误差进行高斯高通滤波处理，以此来更加直观的表征不同频段下面形误差分布情况，下文中图2、3，表1~4及相关段落中的文字描述也使用此方法表达。样件初始面形分布如表1所示。

表1 样件初始面形分布

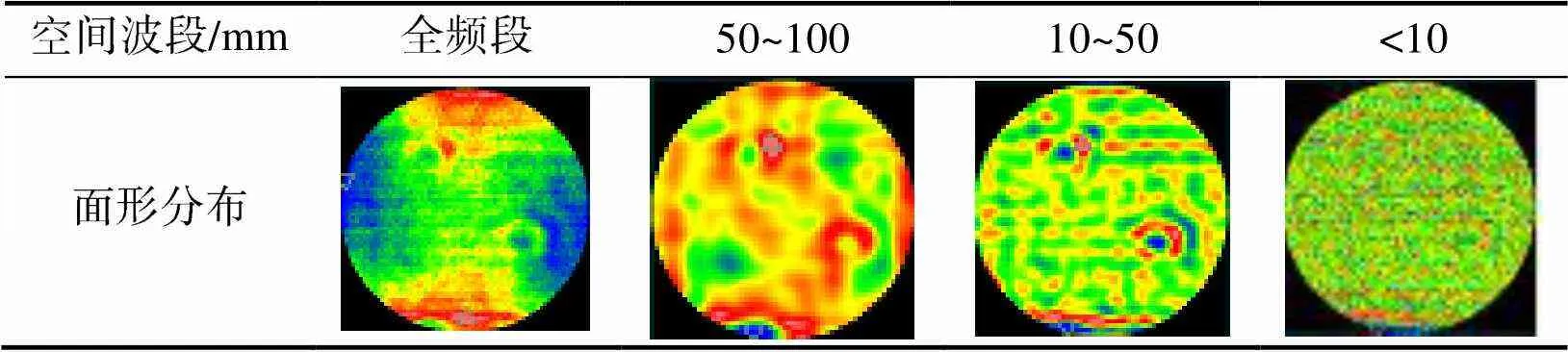
Tab.1 Initial shape error distributions of the sample

通过观察发现初始面形具有如下特点：

1） 初始面形误差主要分布在大于100mm的空间波段，表现为加工中产生的像散类型的低频误差；

2） 在50~100mm空间波段内，面形误差表现为各种高阶的镜面误差，主要为加工产生的低频误差及气流扰动引起的误差；

3） 在10~50mm空间波段内，主要由各种中频段误差组成，包括：“格子效应”、小磨头抛光路径残差以及其他形式的误差，传统抛光方法很难消除；

4） 小于10mm的空间波段内，主要为高频的误差，量值较小。

2.3 试验的理论基础及工艺设计

光学加工中，应努力使实际去除的材料量接近期望去除的材料量，材料的去除有效率定义为

根据定义可知，材料去除有效率0<≤1，越接近1，则面形修正能力越强；反之，则修正能力越弱。考虑离子束的去除函数为近高斯形状，其中心处具有最大去除效率，当去除函数取峰值一半时对应的口径宽度即为半高宽度（FWHM），将去除函数的FWHM定义为，将待加工的反射镜空间波长定义为，通过计算可得材料去除有效率为[20-23]

由式（3）可见，材料去除有效率与去除函数的半高宽度和空间波长都相关。材料去除有效率(,)是变量/的平方的负指数函数，随着/的增大，材料去除有效率迅速下降。

通过调整离子源工艺参数，可获得不同的去除函数，主要工艺参数包括工作气体的流量、电离电压、栅格口径、作用距离及中和电流等，各项参数与去除效率关系如表2所示。

表2 离子源工艺参数与去除效率关系表

Tab.2 The relationship between process parameters and the removal efficiency

根据样件的初始面形和式（3），针对不同频段的面形误差设置不同的工艺参数，第1组与第2、3组比较，其他工艺参数不变的情况下，加大了气体流量与电离电压，第4组与前三组相比，缩小了栅格口径，降低了气体流量、电离电压及作用距离，由此获得了不同的去除函数及不同频段的有效去除率，如表3所示。

表3 不同工艺参数下有效去除率变化表

Tab.3 The change of effective removal rate under different process parameters

3 试验结果及分析

从表1可以看出，空间波段大于100mm的区间，面形误差非常大。因此，首先选用了大口径的离子源进行加工；然后根据加工后的面形测试结果，选用合适的离子源参数进行加工。共经过4轮迭代加工，面形频段误差变化如表4所示。

表4 不同迭代抛光阶段面形误差

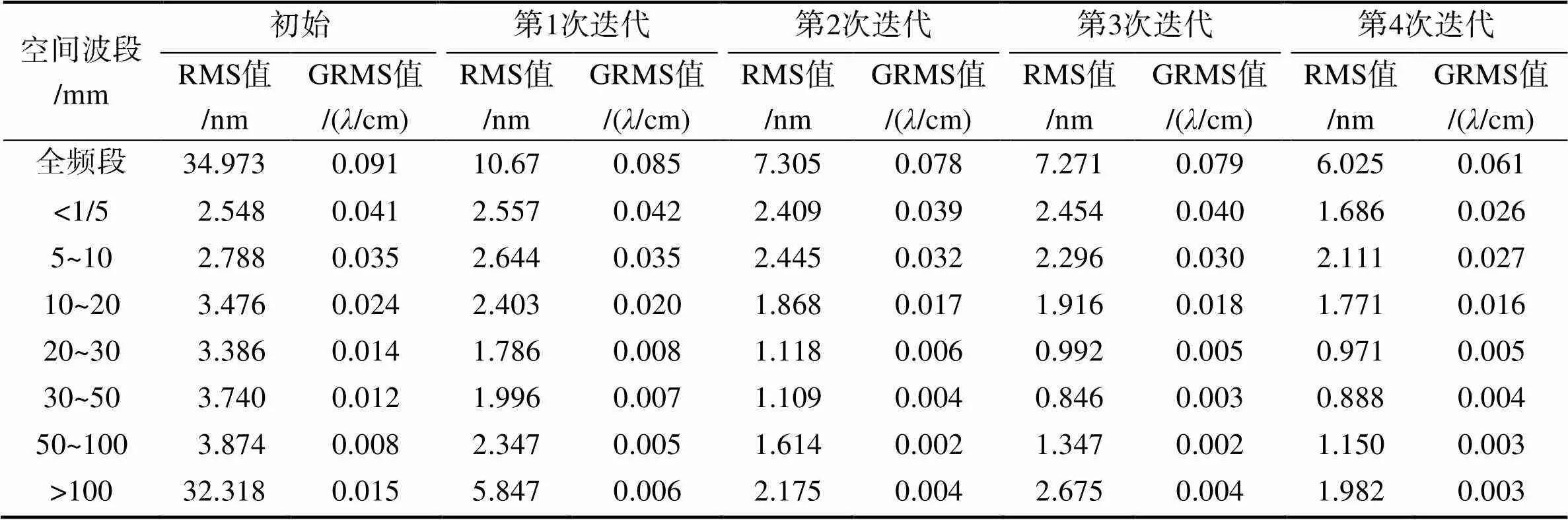
Tab.4 The error of shape in different iterative polishing stages

为使图示更为清晰，将面形频段误差的RMS值、面形梯度误差的GRMS值取对数，可以得出面形误差收敛曲线，如图2所示。

从表2、图2可以得出如下结论：

1） 经过4轮迭代，全频段面形误差RMS值从34.973nm收敛到6.025nm，GRMS值从0.091/cm收敛到0.061/cm；

2） 第1轮离子束加工，使用了FWHM为31mm的去除函数，从图2（a）可以看出：在大于50mm的空间波段，面形RMS值的收敛效率远比10~50mm的高，10mm以下空间波段RMS值基本不收敛；从图2（b）可以看出：大于20mm空间波段，GRMS值收敛效率较高；

3） 第2轮离子束加工，使用了FWHM为18mm的去除函数，从图2（a）和图2（b）可以看出：在大于20mm空间波段面形RMS值和GRMS值得到进一步改善；

图2 离子束加工过程中面形误差收敛曲线

4） 第3轮离子束加工，继续使用FWHM为18mm的去除函数，但峰值去除率略微变小，在整个空间波段范围内，面形RMS值及GRMS值收敛效率均比较低，甚至在大于100mm空间波段，面形RMS值出现反复，主要由加工过程的热效应或测量过程的气流扰动引起的；

5） 第4轮离子束加工，使用了FWHM为9mm的去除函数，由于离子束能量更小，面形RMS值在全频段范围内均小幅收敛；面形GRMS值只在小于10mm空间波段内有实质性的收敛，其他空间波段的GRMS值已趋于饱和。

将面形RMS值及GRMS值绘制到一副图内，如图3所示，经过分析可以发现更多有价值的信息。

图3 面形收敛趋势图

从图3可以看出：

1） 初始面形误差的GRMS值随着空间频段的增加迅速降低，但在大于100mm的空间波段，由于大尺度像散的影响，GRMS值出现反弹；

2） 由于离子束加工对大尺度像散的去除，最终面形误差的GRMS值表现出随空间频段递减的特性，尤其在大于10mm的空间波段，GRMS值显著收敛；

3） 样件面形误差的RMS值在全频段范围内均有效收敛，尤其在10~100mm空间波段范围内；

4） 初始的RMS值和GRMS值的整体变化趋势不一致，可能跟前期抛光工艺不合理相关，导致中频误差的产生；但经过离子束的多轮加工，最终二者的整体变化趋势趋于一致，实现了不同评价指标的同步收敛。

4 结束语

本文以RMS和GRMS指标作为评价参数对非球面反射镜的面形进行分频段评价，分析了直径420mm样件表面误差的特性及来源。根据材料有效收敛率理论，制定了针对性的全频段面形误差去除工艺，通过4轮离子束迭代加工，全频段面形误差RMS值从34.973nm收敛到6.025nm，GRMS值从0.091/cm收敛到0.061/cm，实现频段误差在不同评价参数下的同步收敛。说明离子束修形具有高确定度、高效率的工作特点，在合理的工艺参数下，能够有效去除中大口径元件结构以及前道加工中造成的全频段误差。由于受到设备限制，试验中对于低于200mm口径的小型光学元件收敛效果无法得到进一步验证。在本研究基础上，可进一步挖掘离子束修形潜力，研究定制化波前误差加工的可能性。

[1] 王小勇. 空间光学技术发展与展望[J]. 航天返回与遥感, 2018, 39(4): 79-86. WANG Xiaoyong. Development and Prospect of Space Optical Technology[J]. Spacecraft Recovery & Remote Sensing, 2018, 39(4): 79-86. (in Chinese)

[2] 冯友君, 林中校, 张蓉竹. 连续位相板梯度对焦斑匀滑特性的影响[J]. 物理学报, 2011, 60(10): 1-7. FENG Youjun, LIN Zhongxiao, ZHANG Rongzhu. The Influence of Root Mean Square Phase Gradient of Continuous Phase Plate on Smoothing Focal Spot[J]. Acta Physica Sinica, 2011, 60(10): 1-7. (in Chinese)

[3] PEGRO G R, KIM A D. Comparison of Light Scattering Models for Diffuse Optical Tomography[J]. Optical Express, 2009, 17(11): 8756-8774.

[4] ASADCHIKOVA V E, KOZHEVNIKOV I V, KRIVONOSOY Y S, et al. Application of X-ray Scattering Technique to the Study of Supersmooth Surfaces[J]. Nuclear Instruments and Methods in Physics Research A, 2004, 530: 575-595.

[5] 杨秉新, 曹东晶. “高分二号”卫星高分辨率相机技术创新及启示[J]. 航天返回与遥感, 2015, 36(4): 10-15. YANG Bingxin, CAO Dongjing. The Technology Innovation and Inspiration of GF-2 Satellite High-resolution Camera[J]. Spacecraft Recovery & Remote Sensing, 2015, 36(4): 10-15. (in Chinese)

[6] LODHA G S, KOUJUN Y, HIDEYO I K, et al. Effect of Surface Roughness and Subsurface Damage on Grazing-incidence X-ray Scattering and Specular Reflectance[J]. Applied Optics, 1998, 37(22): 5239-5252.

[7] 杨力. 先进光学制造技术[M]. 北京: 科学出版社, 2001. YANG Li. Advanced Optical Manufacturing Technology[M]. Beijing: Science Press, 2001. (in Chinese)

[8] 戴一帆, 尚文锦, 周旭升. 计算机控制小工具抛光技术中磨盘材料对去除函数的影响[J]. 国防科学技术大学学报, 2006, 28(2): 97-101. DAI Yifan, SHANG Wenjin, ZHOU Xusheng. Effection of the Material of a Small Tool to the Removal Function in Computer Control Optical Polishing[J]. Journal of National University of Defense Technology, 2006, 28(2): 97-101. (in Chinese)

[9] 何曼泽, 王琳, 周佩瑶, 等. 3 mm厚大口径超薄元件双面抛光工艺[J]. 强激光与粒子束, 2013, 25(12): 3315-3317. HE Manze, WANG Lin, ZHOU Peiyao, et al. Double-side Polishing of 3mm Large-aperture Ultra-thin Component[J]. High Power Laser and Particle Beams, 2013, 25(12): 3315-3317. (in Chinese)

[10] NAKAJIMA K, NAKAT'O Y. Low Thermal Expansion Substrate Material for EUVL Components Application[C]//SPIE Microlithography 2005, Feb 27, 2005, San Jose, California, United States. SPIE, 2005: 146-157.

[11] ASCHKE L, SCHWEIZER M, ALKEMPER J, et al. Substrate for the Micro-lithography and Process of Manufacturing Thereof: US, 7279252[P]. 2007-10-09.

[12] GHIGO M, CANESTRARI R, SPIGA D, et al. Correction of High Spatial Frequency Errors on Optical Surfaces by Means of Ion Beam Figuring[J]. Proc. of SPIE, 2007, 6671: 667114.

[13] 钟波, 陈贤华, 王建, 等. 高精度离轴非球面透镜的制造与检测[J]. 红外激光与工程, 2018, 47(7): 200-207. ZHONG Bo, CHEN Xianhua, WANG Jian, et al. Fabrication and Test of High-precision Off-axis Aspheric Lens[J]. Infrared and Laser Engineering, 2018, 47(7): 200-207. (in Chinese)

[14] RICHARD N Y, BENJAMIN B G, BRIAN L S. An Overview of Power Spectral Density (PSD) Calculations[J]. Proc. of SPIE, 2005, 5869: 58690U．

[15] LAWSON J K, AIKENS D M, ENGLISH R E, et al．Power Spectral Density Specifications for High-power Laser Systems[J]. Proc. of SPIE, 1996, 2775: 345-356.

[16] WU B, KUMAR A. Extreme Ultraviolet Lithography: A Review[J]. Journal of Vacuum Science & Technology B, 2007, 25(6): 1743-1761.

[17] GHIGO M, CORNELLI S, CANESTRARI R. Development of a Large Ion Beam Figuring Facility for Correction of Optics up to 1.7m Diameter[J]. Proc. of SPIE, 2009, 7426: 742611.

[18] 解旭辉, 谷文华, 周林. 应用细小离子束加工小型精密光学零件[J]. 国防科技大学学报, 2009, 31(4): 10-14.XIE Xuhui, GU Wenhua, ZHOU Lin. Study on Machining Small Precision Optical Component Using Thin Ion Beam[J]. Journal of National University of Defense Technology, 2009, 31(4): 10-14. (in Chinese)

[19] 王贵林. KDP光学零件超精密车削加工误差的频谱特性与控制[J]. 应用光学, 2017, 38(2): 159-164. WANG Guilin. Spectral Characteristics and Control of Machining Errors of KDP Optical Elements in Ultra-precision Turning[J]. Journal of Applied Optics, 2017, 38(2): 159-164. (in Chinese)

[20] 惠迎雪, 刘卫国, 马占鹏, 等. 射频聚焦离子源熔石英高确定性去除特性研究[J]. 应用光学, 2019, 40(2): 284-290. HUI Yingxue, LIU Weiguo, MA Zhanpeng, et al. Research on High Deterministic Removal Characteristics of Fused Quartz Using RF Focused Ion Beam Source[J]. Journal of Applied Optics, 2019, 40(2): 284-290. (in Chinese)

[21] 张良, 李圣怡, 周林, 等. 基于法拉第杯的离子束抛光机束流密度检测研究[J]. 航空精密制造技术, 2013(6): 8-12. ZHANG Liang, LI Shengyi, ZHOU Lin, et al. Study on Examination of Ion Beam Density of Ion Beam Figuring Machine Based on Faraday Cup[J]. Aviation Precision Manufacturing Technology, 2013(6): 8-12. (in Chinese)

[22] 李云, 邢廷文, 许嘉俊, 等. 三轴离子束抛光系统驻留时间算法[J]. 红外与激光工程, 2012, 41(5): 1300-1305.LI Yun, XING Tingwen, XU Jiajun, et al. Dwelltime Algorithm for the 3-axis Ion Beam Figuring System[J]. Infrared and Laser Engineering, 2012, 41(5): 1300-1305. (in Chinese)

[23] 唐瓦, 邓伟杰, 郑立功, 等. 离子束抛光去除函数计算与抛光实验[J]. 光学精密工程, 2015, 23(1): 31-39. TANG Wa, DENG Weijie, ZHENG Ligong, et al. Calculation of Removal Function of Ion Beam Figuring and Polishing Experiment[J]. Optics and Precision Engineering, 2015, 23(1): 31-39. (in Chinese)

Evolution of Full Band Errors in Ion Beam Processing

LI Wenqing1,2ZHANG Jiyou1,2WANG Yonggang1,2MA Xianmei1MENG Xiaohui1,2LI Ang1,2

（1 Beijing Institute of Space Mechanics and Electricity, Beijing 100094, China）（2 Optical Ultraprecise Processing Technology Innovation Center for Science and Technology Industry of National Defense, Beijing 100094, China）

In the manufacturing process of high-precision optical components in the fields of space optics, lithography objective lens, inertial confinement fusion (ICF), strong light system and others, the shape modification technology based on the principle of small grinding head polishing can effectively remove the low-frequency surface shape error, but it is difficult to correct the medium and high-frequency errors. In order to effectively control the whole frequency range error, this paper takes the aspheric surface with diameter of 420mm as the sample, and carries out the shape modification convergence test of different frequency band errors on the ion beam polishing machine tool. According to the characteristics of the surface shape error of optical elements in different frequency bands, the root mean square (RMS) and gradient root mean square (GRMS) of the surface error frequency band are used as evaluation parameters to analyze the causes of the error in each frequency band, and to explore the corresponding relationship between the process parameters of ion beam and other factors and the errors of each frequency band. After four rounds of ion beam iterative processing, the RMS value of the full band surface shape error of the sample piece converges from 34.973nm to 6.025nm, and the GRMS value converges from 0.091/cm to 0.061/cm (=632.8nm). The experimental results show that: by optimizing the process parameters of ion beam, the shape accuracy of optical elements in full frequency band can be significantly improved, and the synchronous convergence of frequency band error under different evaluation parameters can be realized. The RMS and GRMS indexes can be used as the standards to evaluate the change of surface shape error in the whole frequency band, which has guiding significance for optical processing.

spatial frequency band; full band error; ion beam polishing; process parameters; space remote sensing

TH706

A

1009-8518(2020)05-0047-08

10.3969/j.issn.1009-8518.2020.05.006

2020-04-16

国防科技创新特区项目（19-163-18-ZT-013-023-01）

李文卿, 张继友, 王永刚, 等. 离子束加工中全频段误差的演变[J]. 航天返回与遥感, 2020, 41(5): 47-54.

LI Wenqing, ZHANG Jiyou,WANG Yonggang, et al. Evolution of Full Band Errors in Ion Beam Processing[J]. Spacecraft Recovery & Remote Sensing, 2020, 41(5): 47-54. (in Chinese)

李文卿，男，1982年生，2005年获长春理工大学测控技术与仪器专业学士学位，工程师。主要研究方向为大口径非球面光学元件研制与检测技术。E-mail：vencherl@126.com。

张继友，男，1978年生，2006年获中科院成都光电技术研究所测试计量技术及仪器专业博士学位，研究员。主要研究方向为空间光学先进制造技术。E-mail：jyzhang0627@163.com。

（编辑：庞冰）