基于早期返排历史数据的水平井分段压裂效果评价方法

虞绍永

（达坦能源集团，上海 200433）

目前，超低渗透储层（页岩/致密砂岩）普遍采用水平井分段压裂技术开发，分段压裂作业完成后，需要进行压裂液返排，返排时间一般为15～30 d。压裂液返排制度（包括返排时间、返排期油嘴变化和返排速度）在一定程度上会影响裂缝导流能力，从而影响水平井产量。过去人们对压裂液返排历史数据的重视度和利用率不高，实际上，这些数据对描述水力裂缝特征、深入分析压裂作业效果及产量预测具有重要作用，通过分析这些数据，可以得到初始有效裂缝（水力裂缝与天然裂缝）孔隙体积、返排过程中的裂缝体积损失等参数，进而分析评价返排制度对压裂效果的影响。同时，井下测量技术的发展也极大提高了返排时数据采集的密度和精度，使得利用早期返排历史数据进行水平井分段压裂效果评价成为可能。迄今为止，国外学者在这方面做了许多理论研究，提出了很多返排早期（单相流生产阶段）返排量和压力的计算方法，以及基于压裂液返排历史数据的有效裂缝孔隙体积计算模型[1-8]。然而，这些模型均需要已知水力压裂裂缝压缩系数（以下简称裂缝压缩系数）cf，而cf的计算结果存在较大的不确定性，直接影响了模型计算结果的准确性。为此，笔者基于已有的计算模型，应用产量不稳定试井中的流动物质平衡方法[9]，结合传统的产量递减方法[10]，提高了裂缝压缩系数的计算精度，从而提高了有效裂缝孔隙体积的准确性，为描述水力裂缝特征、评价压裂后效果提供了参考。

1 压裂液返排历史的主要特征

水平井分段压裂后返排作业时间一般都不长，虽然不同水平井的返排制度不同，但其返排历史的主要特征基本类似。压裂液返排期可以分为3个阶段（如图1所示）。

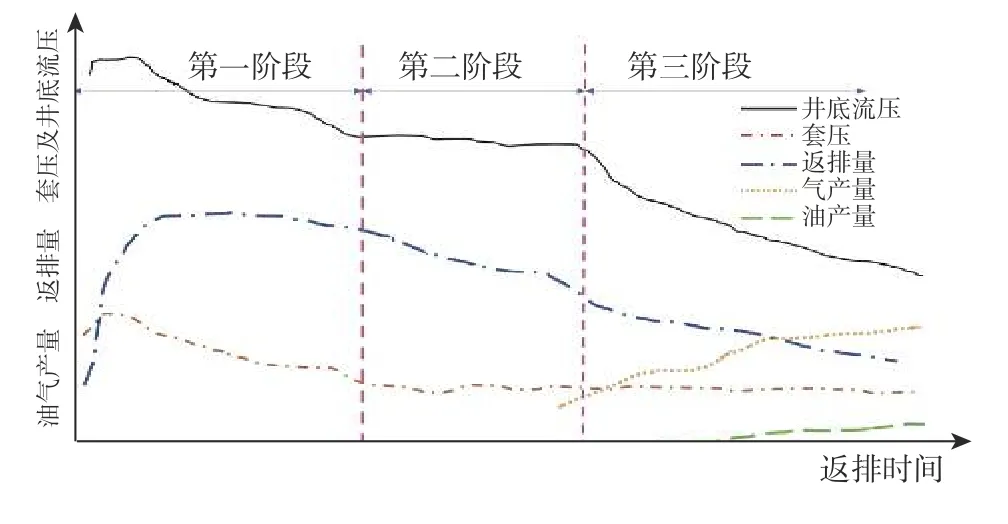
图1 压裂液返排期 3 个阶段的主要特征示意Fig.1 Main characteristics of the three phases during the flowback of fracturing fluid

1）第一阶段：单相压裂液生产。在该阶段，随返排时间增长，套压及井底流压迅速降低，返排量达到峰值后缓慢下降。

2）第二阶段：单相压裂液生产。在该阶段，套压及井底流压基本稳定，后期随着气体开始产出并急剧增加，出现井筒卸载效应（即储层中的气体进入井筒后导致静液压力降低），套压会有所升高。

3）第三阶段：多相流（压裂液、油/气）生产。在该阶段，返排量、井底流压急剧下降，套压持续下降，产气量快速升高。

2 初始压裂效果参数的定义

水平井在进行水力压裂时，井筒周围会形成一个高压力区，迫使压裂液不断向地层滤失。然而，由于致密储层渗透性超低，滤失于基质内的压裂液很少，绝大部分的压裂液将进入水力压裂裂缝中，从而获得很大的裂缝孔隙体积。当压裂作业结束、地面泵压为零后，裂缝孔隙体积可能仍会增大。因此，评价压裂效果，就是要准确计算初始有效裂缝孔隙体积。由于地层存在天然裂缝，而水力压裂裂缝只能沟通部分天然裂缝，未被沟通的天然裂缝，尽管在微地震资料中明显可见，但对水平井产能没有贡献，因此不能算为有效裂缝孔隙体积。压裂液返排过程中，部分裂缝闭合会导致裂缝孔隙体积减小，因此有效裂缝孔隙体积就是初始有效裂缝孔隙体积减去返排过程中损失的裂缝孔隙体积，即:

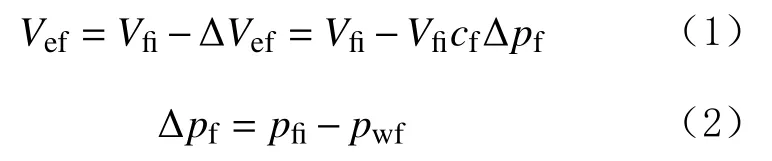
式中：Vef为有效裂缝孔隙体积，m3；Vfi为初始有效裂缝孔隙体积，计算方法见文献[11]，m3；ΔVef为压裂液返排过程中损失的裂缝孔隙体积，m3；cf为裂缝压缩系数，MPa-1；Δpf为返排期间的压力差，MPa；pfi为开始返排时裂缝内的初始压力（可用当时的井底流压来代替），MPa；pwf为井底流压，MPa。

为了更好地表征压裂液返排过程中裂缝闭合、水膨胀及地层流体（油/气）膨胀的影响，引入了相应代表返排驱替能量的指数因子[11]。

1）裂缝压实驱替指数因子ICD。用该因子来反映压裂液返排时有效裂缝闭合引起的压裂液产出情况，其表达式为：

式中：ICD为裂缝压实驱替指数因子；ct为综合压缩系数，MPa-1。

2）油/气膨胀驱替指数因子IHD。用该因子来反映压裂液返排时由油/气膨胀引起的压裂液产出情况，其表达式为：

式中：IHD为油/气膨胀驱替指数因子；Sg为裂缝内含气饱和度；cg为裂缝内气体压缩系数，MPa-1。

现场观察发现，在压裂液返排早期，气井一般会同时产气和产水，而油井则仅产水，因此Sg为0，则IHD也为 0。

3）水膨胀驱替指数因子IWD。用该因子来反映返排时水膨胀引起的压裂液产出情况，其表达式为：

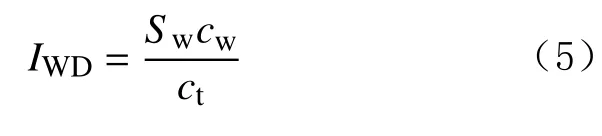
式中：IWD为水膨胀驱替指数因子；Sw为裂缝内含水饱和度；cw为裂缝内水压缩系数。

在压裂液返排期间，油气井的ICD、IHD和IWD的和为1。图2所示为北美某水平井的3个驱替指数因子随返排时间的变化曲线[11]。由图2可知，由于ICD的值最大，所以有效裂缝闭合是该井压裂液返排的主要驱动机制。随着时间的推移，ICD不断减小,IHD不断增大（即返排液中出现油气并不断增多），油/气膨胀成为压裂液返排的重要驱动机制。

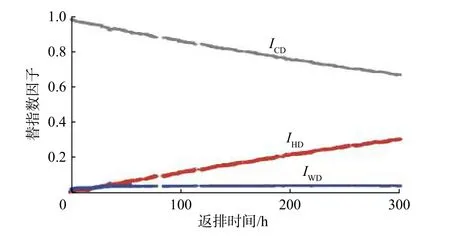
图2 北美某水平井的驱替指数因子随返排时间的变化[11]Fig.2 Variation of displacement index with flowback time for a well in North America[11]

3 有效裂缝孔隙体积的计算方法

有效裂缝孔隙体积的准确计算，关键在于提高裂缝压缩系数cf的准确性。为此，笔者结合产量不稳定试井中流动物质平衡方法和传统的产量递减方法，提高了初始有效裂缝体积和裂缝压缩系数计算的准确性，形成了计算裂缝有效孔隙体积的新方法。

3.1 初始有效裂缝孔隙体积的计算

由式（1）可知，初始有效裂缝孔隙体积Vfi及裂缝压缩系数cf是计算有效裂缝孔隙体积的2个关键参数。考虑到部分压裂液会进入基质中（体积非常小），因而初始有效裂缝孔隙体积Vfi一定小于压裂液注入量VTinj。为此，作如下假设：1）返排压裂液主要从有效裂缝流出，忽略从基质流出的压裂液；2）返排开始时，有效裂缝中仅充满压裂液。

B.Bai等人[12]发现，压裂液返排量可以采用Arps产量调和递减模型计算[3]，即：

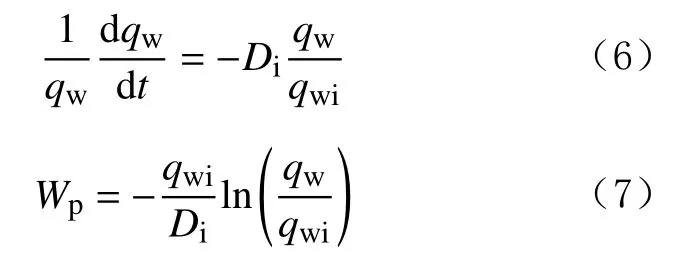
式中：Di为压裂液返排量的初始递减率，1/年；qw为压裂液产量（即返排速度，下同），m3/d；qwi为压裂液初始产量，m3/d；Wp为压裂液累计返排量，m3。

根据式（7），若以Wp为横坐标、qw的对数为纵坐标做图，可发现两者之间基本呈线性关系，如图3(a)所示（BT 代表油/气开始产出的点，下同）。若压裂液返排时井底压力变化很大，需要将压裂液产量进行归一化处理[13]，即纵坐标变为压力归一化产量的对数，则两者之间仍然基本呈线性关系（如图3（b）所示），对应的表达式为：

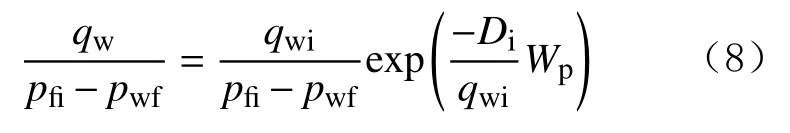
忽略从基质流出的压裂液，有以下近似关系[12-13]：

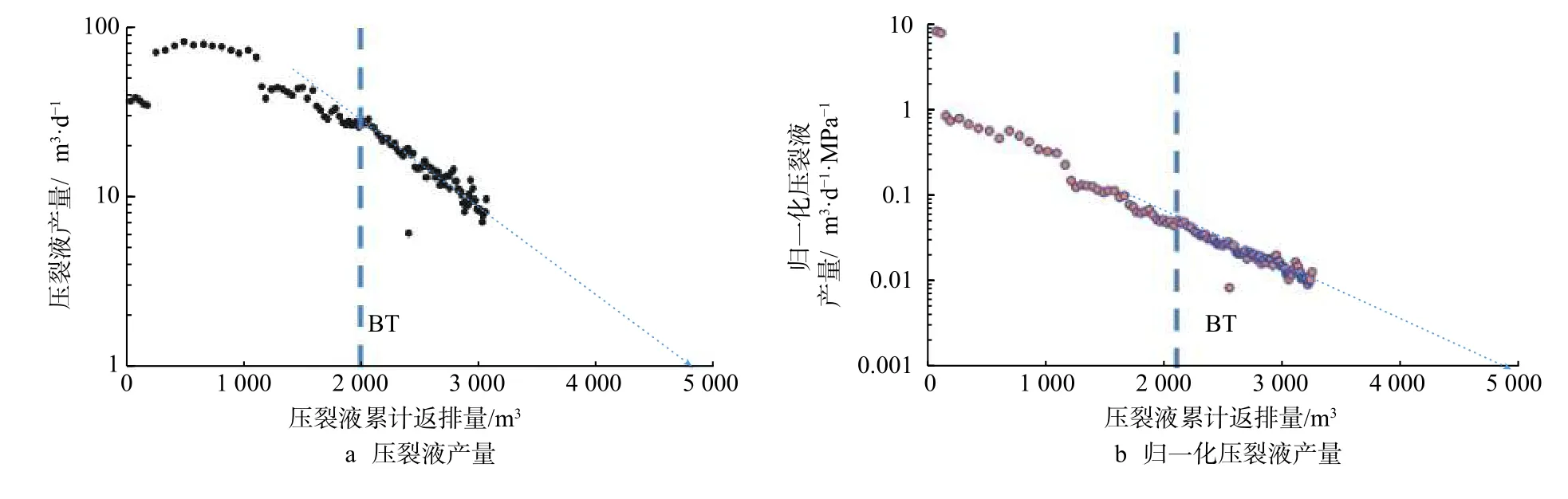
图3 压裂液累计返排量与产量的关系Fig.3 Variation of cumulative fracturing fluid flowback with production

式中：Bwi为压裂液的体积系数，约为1.0；为最终累计返排量（即图3中拟合直线与x轴交点的坐标值），m3。

由式（9）可知，在缺少初始有效裂缝孔隙体积Vfi时，可以用最终累计返排量来代替。

3.2 压裂液返排的主要流动特征

大量研究发现，页岩及致密砂岩油气藏中，水平井分段压裂后压裂液返排通常经历3个流动阶段，如图4所示[14-15]。

图4 压裂液返排主要流动特征示意及特征诊断图Fig.4 Main flow characteristics and diagnostic plot of the fracturing fluid flowback

1）裂缝内的早期线性流或径向流阶段（图4中的FP1）。该阶段中压裂液沿着主裂缝流向井筒，主要流动特征为早期线性流或径向流。若为径向流，则可以利用该阶段压裂液返排历史数据分析求得裂缝渗透率。但在实际应用中，由于返排历史数据的质量问题，且早期受井筒存储效应的影响，很难在流态诊断图上找到该流动阶段，即很难利用该阶段的返排历史数据求解裂缝渗透率。

2）拟稳态流阶段（图4中的FP2）。该阶段为裂缝衰竭/闭合阶段，即随着压裂液产出，裂缝中的压力波不断向外传播，逐渐传播到裂缝与基质的相交处。此时，以裂缝与基质相交处为边界，边界内（裂缝内）流体的流动原理与在推导物质平衡方程时假设油气藏为一个封闭油藏的原理类似。随着压裂液不断流出，裂缝内的压力不断下降，因此裂缝受压缩闭合（类似于裂缝孔隙体积减小）。该阶段压裂液的主要流动特征为产量不稳定试井（RTA）中的拟稳态流，可以通过流动物质平衡方程来计算裂缝孔隙体积。

3）不稳态线性流阶段（图4中的FP3）。随着压裂液不断流向井筒，地层流体开始流入裂缝，与压裂液形成多相流并同时流向井筒，该阶段的主要流动特征一般为不稳态线性流，可以利用该阶段的返排历史数据求得裂缝半长及基质渗透率。

在以归一化压力导数d(Δp/q)/dlntc为纵坐标、物质平衡时间tc为横坐标的流动特征诊断图上，3个压裂液返排阶段的流动特征分别是（如图4（b）所示）：1）曲线斜率为0.5或0时，为不稳态线性流或径向流；2）曲线斜率为1.0时，为拟稳态流；3）曲线斜率等于0.5时，为不稳态线性流。

3.3 裂缝压缩系数cf的计算

国内外众多学者开展了裂缝压缩系数计算方法的研究[7,16]，其中R.Aguilera等人[16]通过室内试验得出裂缝压缩系数与作用在裂缝上的净压力pn及裂缝内“矿物质”的含量有关。净压力是指岩石的最小主应力σmin减去裂缝内的流动压力pf，即：

式中：pn为作用在裂缝上的净压力，MPa；σmin为岩石最小主应力，MPa；pf为裂缝内的流动压力，MPa。

岩石的最小主应力σmin可用裂缝关闭压力pc（可由裂缝诊断注入测试（DFIT）数据分析获取）来代替，而裂缝内的流动压力pf可以用井底流压pwf来代替，则式（10）变为：

式中：pc为裂缝关闭压力，MPa。

R.Aguilera等人[16]绘制的图版如图5所示，不同曲线代表裂缝内“矿物质”（即支撑剂）含量不同。J.D.Williams-Kovacs等人[17-18]认为，“矿物质”含量是指裂缝中支撑剂的体积分数，并与裂缝孔隙度（φf）有关，或者说，“矿物质”含量可以由裂缝孔隙度来表征。由于裂缝孔隙度的真实值较难确定，一般可以给出一个区间值。因此，“矿物质”含量也是一个区间值，裂缝压缩系数也相应地是一个区间值。笔者对图5中的曲线进行了回归分析，得到近似回归方程为：

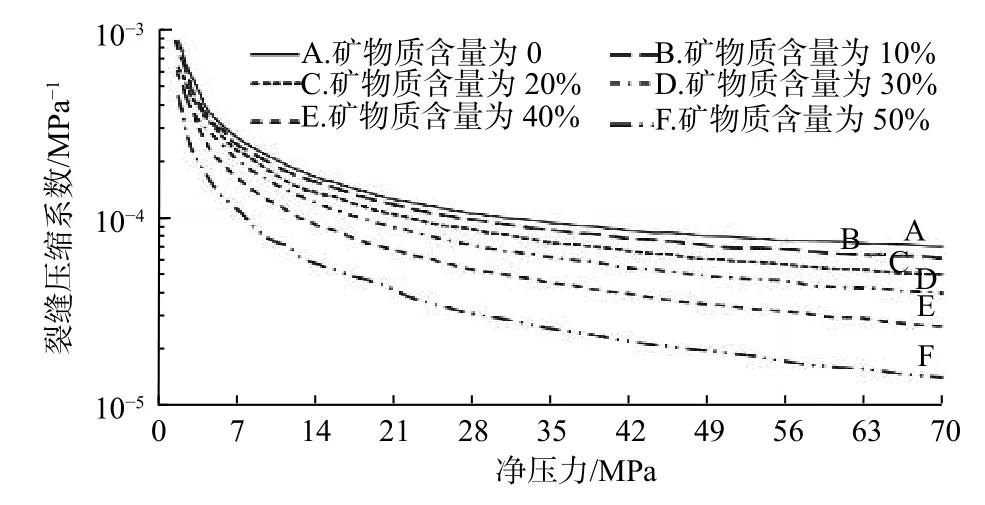
图5 Aguilera等人的裂缝压缩系数图版[16]Fig. 5 Type curves for fracture compressibility coefficient by Aguilera et al.[16]

式中：a和b为回归拟合参数。

回归分析得到，当“矿物质”含量分别为0，10%，20%，30%，40%和50%时，a分别为0.023 8，0.026 1，0.026 4，0.027 4，0.045 6和0.053 0，b分别为0.640，0.663，0.683，0.710，0.809和0.893。

上述裂缝压缩系数计算方法均存在未考虑支撑剂在裂缝中的不均匀分布、不是每口井都有DFIT数据、裂缝孔隙度难以确定等局限性。为此，H.Sabbir等人[13]提出以下假设：1）裂缝最初由压裂液饱和；2）初期裂缝中不存在流动的油气，忽略由基质流入裂缝的油气；3）在拟稳态流阶段，压力随时间的变化是常量，通过裂缝边界控制流（BDF）阶段范围内的数据在时间和空间上取平均值来描述裂缝可压缩性。基于该假设，他们提出了改进的裂缝压缩系数计算方法：

1）整理压裂液返排期的流量及井底流压数据；

2）利用体积系数将地面流量转换成地下流量；

3）计算产量归一化压力RNP及其导数dRNP，以物质平衡时间tc为横坐标，产量归一化压力RNP及其导数dRNP为纵坐标，在双对数坐标系上绘制了如图4（b）所示的压裂液流动特征诊断图；

4）在压裂液流动特征诊断图上找出斜率为1的流动段（边界控制的拟稳态流）的数据，并绘制在线性坐标系上，横坐标为物质平衡时间tc，纵坐标为产量归一化压力RNP，拟合出一条直线，直线段斜率记为mBDF；

5）在半对数坐标系中，作压力归一化产量PNR与累计返排量Wp的关系曲线，拟合直线外推到废弃压裂液返排速度0.16 m3/d、废弃压力0.69 MPa处，废弃点的横坐标值即为最终累计返排量；

6）根据式（9），将初始有效裂缝孔隙体积Vfi近似为最终累计返排量，再利用下式求出cf：

式中：Δpf为返排期拟稳态流阶段的压力差，MPa；pwfe为拟稳态流结束处的井底流压，即在步骤4）中找出的最后一个数据点对应的井底流压，MPa。

分析认为，该计算方法存在3个缺陷：1）因为其理论依据是假设平均裂缝孔隙体积等于初始裂缝孔隙体积与最终裂缝孔隙体积的算术平均值，但实际上裂缝孔隙体积随着压力、裂缝压缩系数、平均含水饱和度等参数的变化而不断变化，且不是一个简单的线性变化过程；2）在用调和递减预测模型计算最终累计返排量时未考虑基质向裂缝的渗流，影响了初始有效裂缝孔隙体积计算结果的准确性；3）未考虑支撑剂的压实效应对裂缝压缩系数的影响。因此，笔者对该方法进行了修正，采用C.R.Clarkson等人[15]提出的流动物质平衡方法计算初始有效裂缝孔隙体积，以压力归一化产量PNR为纵坐标、归一化累计返排量为横坐标作流动物质平衡分析图（如图6所示），拟合直线与x轴交点的横坐标即为初始有效裂缝孔隙体积。

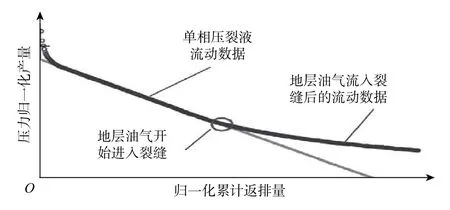
图6 压裂液返排历史的流动物质平衡分析示意Fig.6 Flowing material balance analysis of fracturing fluid flowback history

其中，归一化累计返排量为：

式中：W'p为归一化累计返排量，m3/MPa；φfi为充满支撑剂裂缝的初始孔隙度；φf为充满支撑剂裂缝的孔隙度；为裂缝内平均压力，MPa。

在利用式（17）计算综合压缩系数ct时，需要已知裂缝压缩系数cf。因此，计算过程将是一个迭代过程，可以将由调和递减模型计算得到的最终累计返排量近似为初始有效裂缝孔隙体积，并作为迭代计算的初始值。由此，裂缝压缩系数的计算流程需要增加第7步，即用第6步得到的裂缝压缩系数cf值，再由图6的流动物质平衡曲线得到初始有效裂缝孔隙体积Vfi值，再由式（13）计算cf值。由此迭代，最终分别得到收敛的cf值和Vfi值。

4 计算实例

以国内某致密油水平井A为例，该井采用分段压裂完井，共注入压裂液约17 600 m3，压裂液返排约1个月后开始有油产出，压裂液返排历史如图7所示。

图7 水平井A的压裂液返排历史示意Fig.7 Fracturing fluid flowback history of horizontal well A

根据水平井A的压裂液返排数据，绘制压裂液返排量递减分析图，如图8所示。从图8可以看出，由压裂液返排量递减分析或压力归一化产量递减分析得到的最终累计返排量基本一致，约为6 855.8 m3。用产量归一化压力及其导数、真实时间及物质平衡时间作压裂液流动特征诊断图，见图9。从图9可以看出，流动曲线存在明显的斜率为1的流动段，表明返排期单相压裂液生产阶段，流体流动出现了非常明显的拟稳态流。

选取斜率为1的流动段的数据作产量归一化压力导数与物质平衡时间的关系曲线（如图10所示），求出直线段斜率mBDF为 0.251 8。按上述裂缝压缩系数和初始有效裂缝孔隙体积计算方法，将最终累计返排量的预测值作为初始有效裂缝孔隙体积，由式（13）计算裂缝压缩系数，作流动物质平衡分析图（如图11所示），将数据回归直线与x轴交点的横坐标作为新的初始有效裂缝孔隙体积，代入式（13）再次计算裂缝压缩系数，不断迭代计算，最终得到初始有效裂缝孔隙体积Vfi为6 625.6 m3，裂缝压缩系数cf为0.021 75 MPa-1。

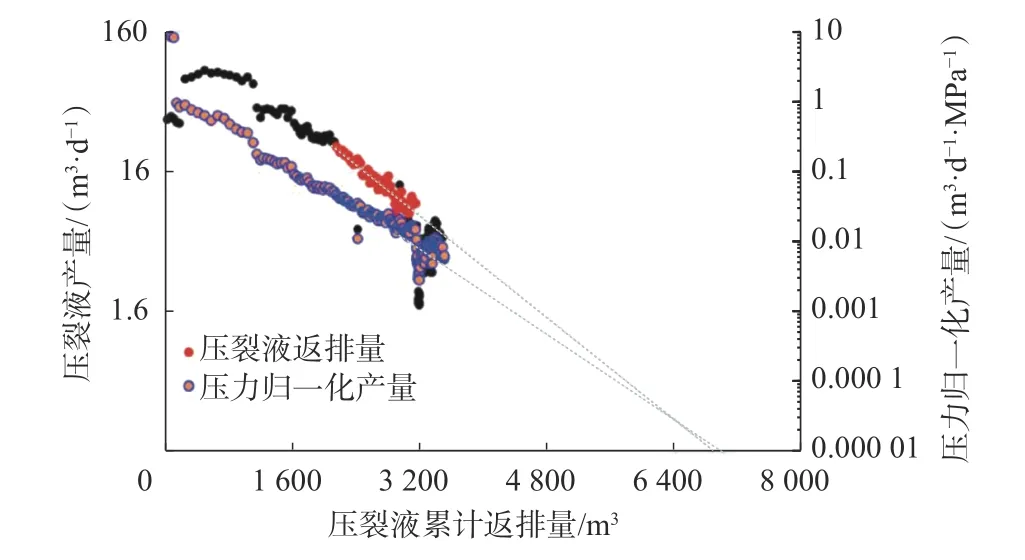
图8 水平井A的压裂液返排量递减分析结果Fig. 8 Decline analysis of fracturing fluid flowback of horizontal well A

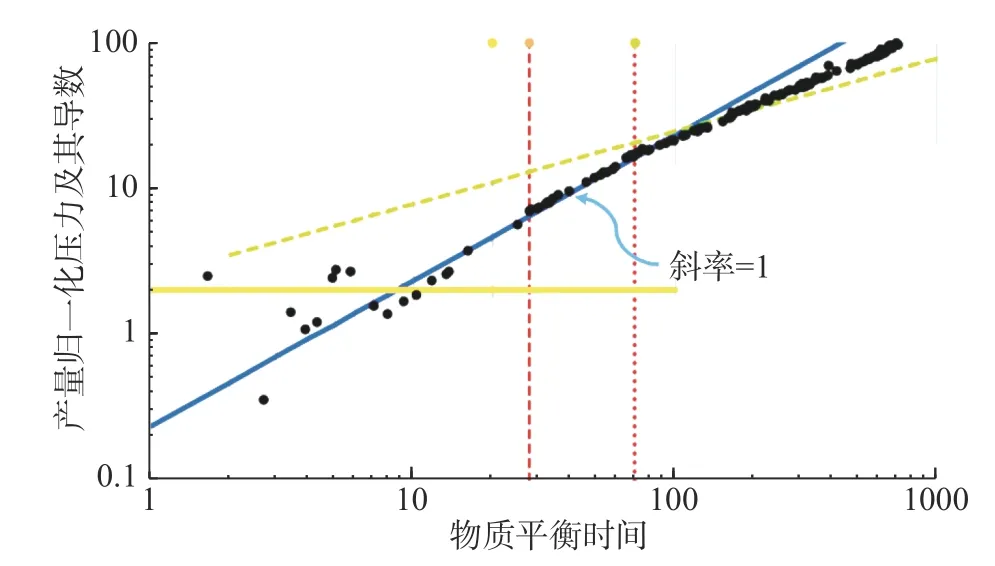
图9 水平井A的压裂液返排流动特征分析诊断图Fig. 9 Flow characteristic diagnostic plot of fracturing fluid flowback of horizontal well A

图10 水平井A的压裂液返排分析特种曲线Fig. 10 Special curve of the fracturing fluid flowback for horizontal well A

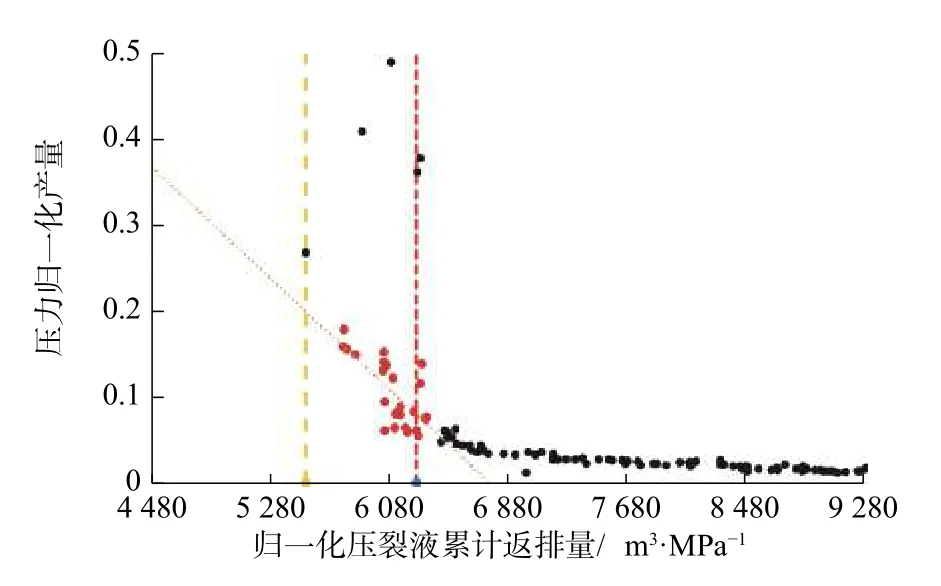
图11 水平井A的压裂液返排期流动物质平衡分析图Fig. 11 Flowing material balance analysis of the fracturing fluid flowback for horizontal well A

水平井A从开始返排到拟稳态结束时的压力差Δpf约为20.13 MPa，因此裂缝体积损失ΔVef=VficfΔpf=20.13×0.021 75×6 625.6=2 902.0 m3，则投产后的有效裂缝孔隙体积Vef=Vfi-ΔVef= 6 625.6 - 2 902.0 =3 723.6 m3，约为压裂液总注入量的21%。也就是说，只 有约21%的压裂液对形成裂缝导流能力有贡献。

5 结 论

1）压裂液返排的地下流体流动机理是裂缝的闭合和流体的膨胀。

2）受裂缝压缩系数计算准确性的影响，基于压裂液返排历史数据的有效裂缝孔隙体积常规计算方法存在计算结果不够准确的问题，笔者结合产量不稳定试井中的流动物质平衡方法和传统的产量递减方法，以提高初始有效裂缝体积和裂缝压缩系数的计算准确性为核心，提出了计算有效裂缝孔隙体积的新方法。

3）计算实例表明，返排期单相压裂液生产阶段，流体流动出现了非常明显的拟稳态流，只有部分注入的压裂液对形成裂缝导流能力有贡献。

4）致密油气藏水平井压裂作业中，地层或多或少地会出现漏失，因此，笔者提出的计算有效裂缝孔隙体积的新方法在对分析致密油气藏水平井压裂液返排历史数据具有比较强的实用性。