宽含水率域桦木应力松弛时温等效研究*
戎建杰 姜志宏
(浙江农林大学,杭州 311300)
近年来,得益于工程木构件的发展,木结构建筑越来越多地在国内外涌现,而发展木结构建筑是未来绿色建筑产业的趋势[1-3]。在生产制造中,木材黏弹性对于木制部件和木结构建筑的长期使用性能和服役寿命有着重要的影响。目前,在木结构安全设计中通常选用与时间无关的恒定参量来考虑力学行为表现,而未考虑与时间相关的木材黏弹性力学行为,这可能无法确保木构件的长期使用性能,问题的根源在于缺乏预测木材长期黏弹性力学行为表现的可靠模型[4]。目前,国内外已有部分关于木材较长期黏弹性试验及其数学模型的研究报道[5-6],但是均不同程度地存在设备有限、试验耗时长、无法精确控制温湿度条件等问题,这些极大地限制了对木材长期黏弹性力学行为的进一步研究。
温度变化对材料的黏弹性力学行为影响很大。温度升高,则应力松弛模量减少。在高分子材料领域,温度与时间对材料黏弹性力学行为的影响存在等效关系,这称之为时温等效。通过时温等效,材料长期黏弹性力学行为的探究可转化为短期试验来进行,这将减少各种限制因素的影响。在木材领域,国内外已有一些学者通过时温等效进行黏弹性力学行为的研究。Samarasinghe[7-12]等研究了时温等效在木材蠕变上的适用性;张红为[13]研究了时温等效在木材应力松弛上的适用性;Salmén[14-19]等研究了时温等效在木材动态黏弹性上的适用性。然而,这些研究大多局限于在单一恒定含水率和单一参考温度条件下讨论时温等效的适用性,而未探讨不同含水率条件和不同参考温度对主曲线和位移因子的影响。换言之,这些研究所涉及的含水率和参考温度比较分散,缺乏宽温度域和宽含水率域范围内的系统研究。本文将在宽温度域和宽含水率域范围内对桦木进行短期弯曲应力松弛试验,运用时温等效获得不同温度和含水率条件下的主曲线,并探究不同位移因子函数的适用性,以期拓展预测木材长期应力松弛行为表现的途径。
1 材料与方法
1.1 材料
木材是变异性很大的生物质材料,为减少木材组织构造差异对试验结果的影响,选取散孔材桦木(Betula pendula)作为试验对象,气干密度范围为0.6~0.7 g/cm3。桦木采用浙江某地板厂的薄板,根据动态热机械分析仪(以下简称DMA)的要求加工成60(顺纹)mm×10 mm×3 mm(L×W×T)的试件。
1.2 设备
DMA(Q800)及其湿度附件,美国TA仪器公司;电子分析天平,瑞士METTLER TOLEDO;电热恒温鼓风干燥箱,上海爱朗仪器有限公司;台锯机,东莞三匠机械有限公司。
1.3 试验方法
1.3.1 试验设计
采用DMA的双悬臂夹具,在不同温度和木材含水率两两组合的条件下进行木材的短期弯曲应力松弛试验。温度变化范围为5~95 ℃,以5 ℃为起始试验温度,之后每隔10 ℃为一个试验温度直至95 ℃,共计10个试验温度;桦木试件含水率选取0%、6%、12%、18%和24%。两个变量进行全因子组合,共计50组试验。由于DMA可设置自动升温程序,加之湿度附件可以由程序来控制相对湿度,因此同一试件可在含水率保持相对稳定的条件下连续完成不同温度水平的应力松弛试验。
1.3.2 试件处理
在进行应力松弛试验前,需要先进行含水率调整处理,以使试件达到试验所需的不同含水率水平。首先,将试件在(103±2)℃的条件下烘至绝干。其中,将绝干试件作为0%含水率试件用于应力松弛试验。随后,将余下的试件在自制的调湿装置中分别调节至6%、12%、18%和24%。当桦木试件含水率达到试验所需含水率水平后(称重后计算),将试件包覆在塑料袋中进行平衡处理,以备试验之用。在进行试验之前,需再一次称重确认试件含水率情况,确保试件实际含水率与试验所需的名义含水率之差在±0.3%之内。
1.3.3 试验过程中试件含水率控制
为了避免试验过程中试件含水率波动对应力松弛试验结果的影响,需要保证试验过程中试件含水率稳定。根据现有研究结果[20],通过对试件包覆PVDC(聚偏二氯乙烯)薄膜同时设置DMA湿度附件参数,以便桦木试件的含水率在应力松弛试验过程中保持稳定。
1.3.4 应力松弛试验
在Stress Relaxation(应力松弛)模式下,设定好升温程序和各温度下最佳的相对湿度参数。在含水率保持稳定的条件下,同一试件依次完成10 个温度水平的应力松弛试验。每个温度水平的应力松弛试验过程为升温-等温-应力松弛三个阶段,各阶段时间分别为15、10 min和30 min。其中,在应力松弛阶段对试件施加0.06%的恒定应变;而在升温和等温阶段不施加应变,这两阶段可视为应力松弛的回复时间。
由于初始应力不同,应力松弛后的残余应力也不同,因此使用残余应力等物理量来表征桦木的应力松弛行为不可行。松弛模量表示的是材料随时间变化的单位应变条件下应力的变化情况,采用这一物理量表征应力松弛行为则具有科学性和普适性,因此本文将用松弛模量表征应力松弛的试验结果。
2 结果与分析
2.1 时温等效可行性分析
由应力松弛试验可得一系列温度和含水率两因素组合条件下的松弛模量曲线谱图。图1 是典型的松弛模量对数时间谱,表征的是桦木在含水率为12%时不同温度水平下的应力松弛行为。由图1 可看出,如果作一条平行于横坐标轴的等松弛模量线(以下简称等模量线),则这条等模量线将与温度为65、55、45、35、25 ℃的松弛模量曲线依次分别相交于a、b、c、d、e点。这表明,当试件所处试验温度为25、35、45、55、65 ℃时,松弛模量可以在不同时间点达到相同值。并且温度越高,则时间点越前。换言之,当温度升高时,松弛模量曲线将向对数时间短的方向移动。理论上,5 ℃和15 ℃时的松弛模量曲线会在更长的时间点与等模量线相交,而75、85、95 ℃时的松弛模量会在更短的时间点与等模量线相交。
当含水率为0 %、6 %、18 %和24 %时,桦木在不同温度水平条件下的松弛模量对数时间谱均呈现出与上述相似的情况。这可认为,在恒定含水率条件下温度的变化只是改变桦木的应力松弛速率,温度越高,则发生应力松弛行为的速度越快,即存在桦木在较高温度、较短时间内的应力松弛量与其在较低温度、较长时间内的应力松弛量相一致的情况。这就是时间与温度对木材应力松弛行为的影响存在等效性的定性表达,称为时温等效。
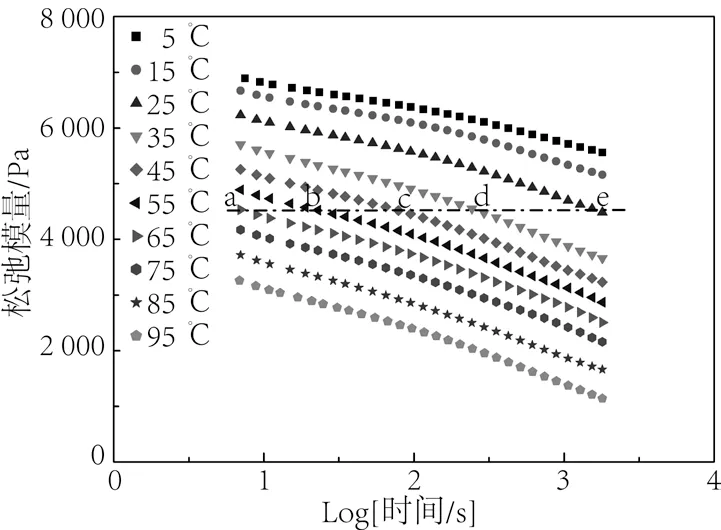
图1 含水率为12 %时不同温度水平下松弛模量对数时间谱Fig.1 Logarithmic time spectrum of relaxation modulus at different temperature levels when moisture content is 12 %
2.2 主曲线及其影响因子分析
2.2.1 主曲线合成
由上述时温等效的定性表达可知,通过不同温度水平条件下的短时间应力松弛试验可预测桦木在某一温度条件下的短时间及长期范围内的应力松弛行为表现。以恒定含水率为12 %时桦木在不同温度水平的应力松弛试验数据为例,对如何利用松弛模量对数时间谱图进行应力松弛行为预测加以说明。首先,在某一恒定含水率条件下,进行不同温度水平的短期应力松弛试验,以获得松弛模量对数时间谱。其次,选取其中某一温度的松弛模量曲线为参考松弛模量曲线,其温度称为参考温度Tref,则根据时温等效的定性表达,可将任一温度T≠Tref的松弛模量曲线沿对数时间轴平移某一数值,使相邻温度的松弛模量曲线在同一模量值处叠合,从而得到一条代替原始曲线族的松弛模量主曲线。如选择25 ℃为参考温度,则将温度高于25 ℃的松弛模量曲线依次向右水平移动,即可预测较长期的应力松弛行为;而温度低于25 ℃的松弛模量曲线依次向左水平移动,即可预测短时间内的应力松弛行为(可以假想为试件受力后瞬间的应力松弛行为)。由此,可得到含水率为12 %时参考温度为25 ℃的松弛模量主曲线。如图2 所示,该松弛模量主曲线可预测应力松弛行为的时间跨度为10-0.47~106.49s(36 d)。

图2 含水率为12 %时参考温度为25 ℃的主曲线Fig.2 Master curve with a reference temperature of 25 °C when moisture content is 12 %
2.2.2 含水率和参考温度对主曲线的影响
为考察时温等效在宽含水率域和不同参考温度条件下的适用性,从含水率和参考温度这两个维度对主曲线进行影响因子分析。
按上述方法合成主曲线,可得5 个恒定含水率时不同参考温度条件下的松弛模量主曲线族,如图3 所示。从图3(a)-(e)中可看到,在任一相同参考温度条件下,当含水率不同时,主曲线的时间跨度范围均不同。比如,当参考温度为25 ℃时,在含水率为0 %时可得到一条预测时间跨度为10-0.50~105.17s(41 h)的主曲线;在含水率为12 %时可得到一条预测时间跨度为10-0.47~106.49s(36 d)的主曲线;在含水率为24 %时可得到一条预测时间跨度为10-0.56~107.63s(1.4 y)的主曲线。


图3 恒定含水率时不同参考温度的主曲线族Fig.3 Master curves of different reference temperature at constant moisture content
当含水率恒定时选取不同温度为参考温度,在0%~24 %的含水率范围内,得到的相应主曲线的形状基本相似,这表明当桦木试件的含水率相对恒定时,温度的变化对于材料的长期力学行为表现只是改变应力松弛速率。利用插值法,由这些谱图可大致预测恒定含水率条件下5~95 ℃范围内任意温度水平的木材应力松弛行为。当然,从木材的实际用途而言,选择较高温度作为参考基准不太合适,因为由此得到的主曲线预测时间跨度会移向短时间,而其长期预测能力减弱。
2.3 位移因子函数
2.3.1 位移因子函数模型
在主曲线合成中,松弛模量曲线的水平位移量称之为时温等效位移因子,记为Log aT,其数值可由公式(1)得到:

式中:Log aT——位移因子;
Log t——任意温度条件下的松弛模量曲线的时间点;
Log tref——参考温度时松弛模量曲线的时间点。
由前述主曲线合成过程可知,在恒定含水率条件下,选定参考温度后,对温度T≠Tref的松弛模量曲线进行水平移动,可得一组位移因子,这将反映Log aT随温度变化的函数关系,即时温等效位移因子函数。
由参考温度对主曲线的影响可知,温度的改变相当于松弛模量主曲线通过位移因子的水平移动。为了从定量角度预测恒定含水率时宽温度域内的木材应力松弛行为,需进一步利用时温等效位移因子函数来探究主曲线合成中位移因子与温度之间的关系,以探寻适合木材应力松弛行为的时温等效经验公式。
在时温等效中,描述位移因子函数Log aT= ƒ(T,Tref)的数学表达式可为:

式中:Log aT——位移因子;
T——任意温度,K;
Tref——参考温度,K;
D1、D——拟合参数;
ΔE——表观活化能,J/mol;
R——摩尔气体常量,J/(mol·K)。
其中,公式(2)为WLF方程,公式(3)为Arrhenius方程。一般而言,WLF方程适用于试验温度高于Tg(即玻璃化转变温度)的情况,而Arrhenius方程适用于试验温度低于Tg的情况。本文考察这两个数学表达式的适用性,主要考虑到以下两方面因素:1)尽管许多研究认为,木材半纤维素和木质素存在玻璃化转变温度,但由于木材中起骨架作用的主要物质纤维素不存在玻璃化转变温度,因此实际上木材的玻璃化转变温度并不明显,故本文未对恒定含水率为0%~24 %范围内的桦木玻璃化转变温度进行探究;2)根据文献[21-22],WLF方程不仅可由Doolittle方程推导获得,也可由Arrhenius方程推导得出。因此本文不考虑Tg对WLF方程和Arrhenius方程的适用性限制,而是在本文研究的试验条件下同时考察这两个数学表达式的适用性。
在5 个恒定含水率条件下,对不同参考温度的位移因子数据分别用公式(2)和公式(3)进行拟合,可得相应拟合参数D1、D2和表观活化能ΔE的值。
2.3.2 含水率和参考温度对位移因子函数的影响
为考察公式(2)和公式(3)在宽含水率域和不同参考温度条件下得到的位移因子的适用性,从含水率和参考温度两个维度,对前述两个数学表达式进行影响因子分析十分必要。
表1 所列为经公式(2)拟合得到的参数D1和D2值。由表1 可看出,D1和D2受含水率和参考温度的影响,但是未呈现明显的规律性,且D1和D2在不同条件下的差异性很大。如含水率为0 %、参考温度为85 ℃时的D1和D2值分别为-42.0 和-1 864,而含水率6 %、参考温度为75 ℃时的D1和D2值分别为63.1 和1 949。
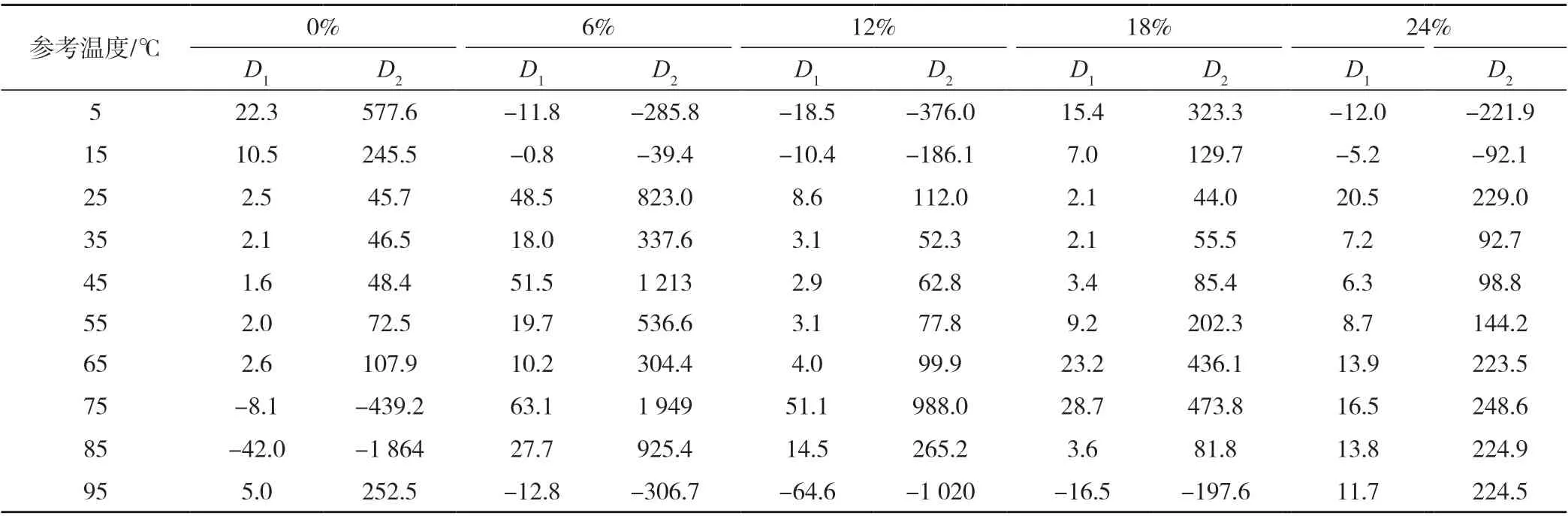
表1 公式(2)中的拟合参数Tab.1 The values of fitting parameter in formula (2)
表2 所列为经公式(2)拟合后得到的决定系数。由表2 可看出,在5 个恒定含水率时不同参考温度条件下的拟合程度均较高,这表明通过公式(2)能较为准确地得到含水率为0%~24 %范围内不同参考温度条件下的位移因子。

表2 公式(2)拟合的决定系数(R2)Tab.2 Coefficient of determination (R2) for formula (2)
表3 所列为经公式(3)拟合而计算得到的表观活化能。由表3 可知,从参考温度相同的角度看,当参考温度为5~45 ℃时,除了含水率为18 %外,表观活化能随着含水率的升高而升高;当参考温度为55~85 ℃时,含水率为6 %的表观活化能最小,含水率为12 %和18 %的表观活化能较为接近,而含水率为24 %的表观活化能最大;当参考温度为95 ℃时,随着含水率的升高,表观活化能逐渐增大。

表3 公式(3)中的表观活化能Tab.3 The values of apparent activation energy in formula (3)
从恒定含水率相同的角度看,当含水率为0 %或6 %时,随着参考温度的升高,表观活化能总体先升后降;当含水率为12 %、18 %或24 %时,活化能总体上随着参考温度的升高而增大。
张红为[13]在含水率为11 %条件下,通过时温等效得到参考温度为10 ℃的杨木三点弯曲的松弛模量主曲线的表观活化能为21.6 kcal/mol(90.29 kJ/mol);通过时间-温度-含水率等效,选择参考温度和含水率分别为60 ℃和3.1 %,Wolcott等[23]得到黄杨拉伸性能的松弛模量主曲线的表观活化能为171 kJ/mol。相较而言,在含水率和参考温度分别相类似的条件下,本文得到的表观活化能与前者较为接近,而与后者的表观活化能差距较大。不过,Wolcott等测的是木材拉伸性能,表观活化能试验结果有差异也是合理的。
表4 所列的是经公式(3)拟合之后得到的决定系数。由表4 可看出,在5 个恒定含水率时不同参考温度条件下的拟合程度都比较高,这表明通过公式(3)能较为准确地得到含水率为0%~24 %范围内不同参考温度条件下的位移因子。

表4 公式(3)拟合的决定系数(R2)Tab.4 Coefficient of determination for (R2) formula (3)
尽管一些学者认为[24-28],在某些温度范围内,Arrhenius方程比WLF方程更适用于描述位移因子和温度之间的关系。但是,通过上述分析发现,在本文研究的温度范围内,Arrhenius方程并未比WLF方程更适用于描述位移因子和温度之间的关系。
3 结论
1)研究表明,桦木应力松弛行为存在时温等效关系,其适用于5~95 ℃的温度范围和0%~24 %的含水率范围。
2)主曲线会受到含水率和参考温度的影响。当恒定含水率在0%~24 %范围内时,可根据已知谱图大致预测5~95 ℃范围内任意温度条件下的桦木长期应力松弛。
3)位移因子函数会受到含水率和参考温度影响。无论WLF方程或Arrhenius方程,其拟合参数或表观活化能,都会随着含水率和参考温度改变而变化。从决定系数看,WLF方程和Arrhenius方程均能较为准确地得到不同温度和含水率条件下的位移因子。

