小跨高比空心胶合木梁抗弯性能研究*

尚 澎 孙友富

（1.南京艺术学院设计学院，南京 210013; 2.南京林业大学材料科学与工程学院，南京 210037）

胶合木梁是一种优质木结构建筑材料，国内外学者对其进行了广泛研究[1-5]。但试验研究采用的胶合木梁多杆件细长，在外部弯矩作用下，承载力较低，挠度较大，中性轴附近应变和应力较小，导致材料性能未能得到充分利用[6-9]。为对胶合木梁进一步优化及有效利用小径级木材，本文提出了一种具有空心截面的胶合木梁，其自重较轻且具较高强重比，梁截面内部的中空构造可用于安置各类管线，增加建筑结构净空。目前针对空心木梁的研究较少，其中，周乾等[10-14]对叠合梁、组合梁等结构形式木梁进行了弯曲性能试验，结果表明：工字梁等组合梁的极限承载力与矩形截面实心梁相差不大，同时腹板对此类梁的力学性能和变形能力有重要影响。Patterson等[15-18]通过对小径级胶合木梁抗弯性能的试验研究，得出空心梁弹性模量与实心梁无显著差异，且其抗弯承载力是美国NDS（National design specification for wood construction）规范预估值的3.7 倍的结论。我国GB/T 50329—2012《木结构试验方法标准》[19]建议采用跨高比≥18 的梁进行受弯试验，试验结果为试件多呈现梁底木纤维拉伸破坏现象。相关规范暂未有关于胶合木梁的跨高比小于此建议值时的破坏机制阐述，部分学者对此情况下的胶合梁进行了抗弯性能的研究[20-22]，结果表明：小跨高比胶合木梁的破坏形式同时具有拉伸破坏及剪切破坏，且梁的极限承载力与截面高度、腹板宽度、剪跨比关联。

为拓展空心胶合木梁的工程应用，本文通过对24根小跨高比胶合木梁的抗弯性能试验，研究不同空心截面尺寸下，空心胶合木梁的破坏形态、承载力及变形情况。

1 材料与方法

1.1 试件设计

选取小径级兴安落叶松（Larix gmelinii）（含水率12.92%，密度0.62 g/cm3）制作胶合木梁试件，顺纹抗压强度43.29 MPa，顺纹抗拉强度89.63 MPa，顺纹抗剪强度5.8 MPa，顺纹弹性模量10 673 MPa。参照GB/T 50329—2012《木结构试验方法标准》和ASTM D198—15《Standard Test Methods of Static Tests of Lumber in Structural Sizes》[23]中的规定, 共设计24根胶合木梁试件，其中包含3 根实心胶合木梁及21 根空心胶合木梁，试件尺寸为100 mm×200 mm×3 000 mm（宽×高×长），跨高比为13.5，剪跨比为4.5。胶合木加工采用YJ-108单组份聚氨酯胶黏剂（固体含量100%，黏度2.4 Pa·s）双面施胶，施胶量220 g/m2，压机施压1.5 MPa，保压6 h。试件共分为8 组，HL-1 组为对比实心胶合木梁，包括3根试件；JHL-2～8 组为不同截面的空心胶合木梁，每组各包括3 根试件。各试件参数见表1，截面形式见图1。

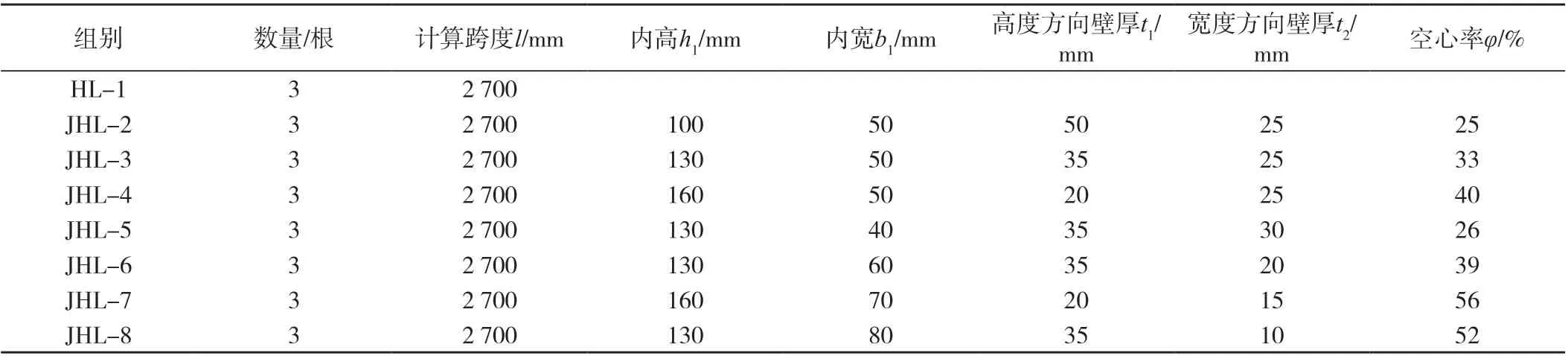
表1 试件设计方案Tab.1 Design Scheme of specimens

图1 试件截面形式（mm）Fig.1 Cross-section configuration of the specimens(mm)

1.2 试验方法

参照ASTM D198—15 标准对试件采用三分点弯曲加载方式。试验采用微机控制的电液伺服机（型号：MS-300，杭州邦威机电控制工程有限公司），作动器最大推力300 kN，荷载P通过分配梁传递。梁的两端支座处设顶针式位移传感器（型号：YHD-50，溧阳市仪表厂），梁跨中处下方设激光位移传感器[型号：KEYENCE IL-300，基恩士（中国）有限公司]，分别量测梁两端支座沉降及跨中挠度变化，精度为0.001 mm，梁跨中沿高度方向均匀分布5 个应变片，梁顶和梁底各设1 个应变片（型号：BX120-30AA，台州市黄岩巨星电测元件厂），所有量测数据由TDS-530 静态数据采集仪同步采集。试验装置及测点布置见图2。正式加载前，对试件进行预加载。正式加载时，先反复进行5 次力控制的加载过程，通过式（1）计算梁的弯曲刚度并记录。随后采用 5 mm/min匀速单调加载，直至试件破坏。

式中：Eexp为试件的弹性模量，MPa；I为试件的惯性矩，mm4；a为加载点至支座的距离，mm；l为试件的计算跨度，mm；F1、F0为40%、10%预估极限荷载值，kN；ω1、ω0为F1、F0对应的跨中挠度值，mm。

图2 试验加载装置Fig.2 Test set-up

2 结果与分析

各试件的极限荷载、跨中挠度、位移延性等试验结果统计数据，见表2。

2.1 试验现象

试件具有3 种破坏形态与特征（图3）。每组试件初期力控制的反复加载过程均处于弹性阶段。循环完成后，随载荷增加，a.梁挠度变形逐渐明显，梁底出现交叉状裂纹并伴随撕裂声，达极限荷载后直至试件被破坏，实心梁HL-1 及空心梁JHL-2 底部仍有相对缓和的纤断断裂过程，且梁底拉伸破坏的形态表现出一定延性特征，而其他空心梁则迅速破坏，呈脆性破坏特征；b.空心梁两侧中性轴及下部出现斜纵向裂纹并迅速发展，破坏时无显著征兆，呈脆性特征的顺纹剪切破坏。c.空心梁受拉部位有明显木节（JHL-4 组及JHL-6组各一试件），随荷载增加，裂纹迅速发展，加载至21 kN及43 kN时，木节处受拉破坏，裂缝迅速发展，试件破坏，这种破坏方式属梁底拉伸破坏，同时局部出现剪切破坏特征。因此，实心梁HL-1 及空心梁JHL-2～6 试件呈梁底拉伸破坏模式，空心梁JHL-7～8 试件为剪切破坏模式。

图3 试件的破坏形态与特征Fig.3 Failure modes and characteristics of specimen

剪跨比是梁上荷载作用点到支座的最小距离与截面高度之比。ASTM D198—15 规范建立了木梁剪跨比与破坏形态的关系：剪跨比小于2.5 时，绝大多数梁发生剪切破坏；剪跨比大于2.5 小于6 时，梁既存在剪切破坏的现象，也有拉伸破坏的现象；剪跨比大于6 时，剪应力即可忽略，梁发生弯曲破坏。跨高比是梁计算跨度与截面高度之比。此三分点加载试验结果表明，剪跨比为4.5，跨高比为13.5 的空心梁试件，符合ASTM关于剪跨比大于2.5 小于6（即跨高比大于7.5 小于18）时，同时具有剪切破坏及拉伸破坏现象的推论，试件以发生梁底拉伸破坏为主，少部分发生剪切破坏现象。

2.2 荷载-挠度曲线

各试件的荷载-挠度曲线见图4。自加载开始至70%极限荷载左右，荷载-挠度曲线近似为直线，呈弹性受弯特征；其后至极限荷载间，曲线呈非线性。实心梁HL-1 及空心梁JHL-2 达到极限荷载后，随荷载增加，其荷载-挠度曲线斜率逐渐减小，出现一定塑性受弯特征。而其他空心梁试件达极限荷载后即迅速破坏，荷载大幅下降，反映为脆性破坏的特征。

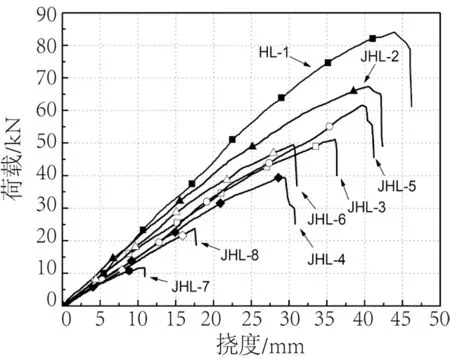
图4 荷载-挠度曲线Fig.4 Load-deflection curves

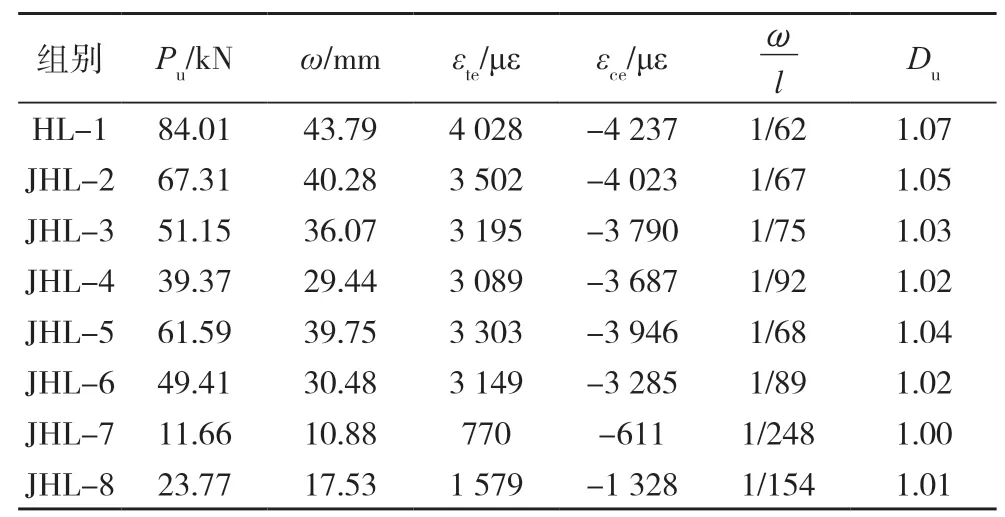
表2 受弯试验结果Tab.2 Results of bending test

GB 50005—2017《木结构设计标准》[24]规定，梁跨中挠度设计限值应小于l/250。除JHL-7 以外的试件在挠度小于l/250 的正常使用极限状态时（即10.8 mm），荷载-挠度曲线基本为直线，这与本试验中试验现象相符；而JHL-7 试件则已破坏，故不符合结构要求。JHL-2～6 及JHL-8 试件在达到极限荷载时的平均挠度为32.26 mm，远大于设计限值，约为后者的2.99 倍；同时其最大挠度40.28 mm可达l/67。因此，根据结构承载极限状态下的破坏不应早于正常使用极限状态下破坏的设计原则，空心胶合木梁的结构设计指标为挠度变形而非强度。空心率≤52%，高度方向壁厚≥ 20 mm的空心梁试件JHL-2～6、JHL-8 的截面尺寸及强度符合结构要求。

2.3 截面应变分布

图5 截面高度-应变曲线 Fig.5 Section height-strain curves of representative specimens

分别选取实心梁、拉伸破坏空心梁、剪切破坏空心梁典型试件，得到其跨中截面高度-应变关系曲线，见图5。从图中可看出，包络线从加载开始到试件破坏近似保持线性，各组试件的跨中截面应变分布基本符合平截面假定。

空心梁截面壁厚与极限拉应变的关系，见图6。图中可见，发生拉伸破坏的JHL-2～6 试件明显区别于发生剪切破坏的JHL-7～8 试件。即当20 mm≤t1≤ 50 mm，同时20 mm≤t2≤30 mm时，空心截面尺寸变化对梁底极限拉应变的影响较小。截面宽度方向壁厚t2＜20 mm时，JHL-7～8 试件极限拉应变突降，这是由于受弯过程中过早发生剪切破坏，并受木节等缺陷影响且材料强度未得到充分利用。因此，在工程设计中空心胶合木梁的截面宽度方面壁厚应≥20 mm。

图6 空心截面壁厚与极限拉应变关系 Fig.6 Relationship between the wall thickness and ultimate strain

2.4 极限承载力、位移延性

空心梁JHL-2～8 相对实心梁HL-1，截面面积分别减少25%、26%、33%、39%、40%、52%、56%，极限荷载则相对减少19.9%、26.7%、39.1%、41.2%、53.1%、71.8%、86.1%，表明试件空心率与极限承载力基本呈反比例关系。空心梁极限荷载与空心率的变化关系见图7。图中可见，宽度方向壁厚均为25 mm的试件（JHL-2，JHL-3，JHL-4）；以及高度方向壁厚均为35 mm的试件（JHL-5，JHL-3，JHL-6，JHL-8），其极限荷载随空心率增长而下降。

图7 极限荷载-空心率关系曲线Fig.7 Relationship between ultimate load and hollow radio

位移延性指结构或构件由弯曲开始至极限承载力或达到后而承载力无明显下降阶段的变形能力。试件延性系数越大，后期变形能力越大（结构弯曲后仍可继续承受较大的塑性变形而不至于发生结构整体破坏的能力）。胶合木梁试件的荷载-挠度曲线无显著屈服平台和下降段，因此，延性系数Du定义为：

式中：Δu为试件所受荷载下降至85%极限承载力时的跨中挠度，mm；Δy为试件达到极限承载力时的跨中挠度，mm。

由表2 结果可知，各试件的位移延性与极限承载力基本成正比例关系，且延性系数随空心率的增大而减小，随截面高度方向壁厚的减小而减小，与宽度方向壁厚无明显相关性。

2.5 弯曲刚度

取各试件0～0.4Pu时的割线刚度为试件的初始弯曲刚度[25]，试验弯曲刚度由试验所得，理论弯曲刚度为考虑胶合木材料充分利用情况下的计算刚度，各试件刚度对比见表3。

发生拉伸破坏的空心梁试件（JHL-2～6）试验弯曲刚度与理论弯曲刚度之比的平均值为0.89；发生剪切破坏的空心梁试件（JHL-7～8），试验弯曲刚度与理论弯曲刚度之比的平均值为0.84。除去不符合结构要求的JHL-7 试件，其余空心梁试件的试验弯曲刚度与理论弯曲刚度之比为0.88，在进行其变形计算时应予以考虑。

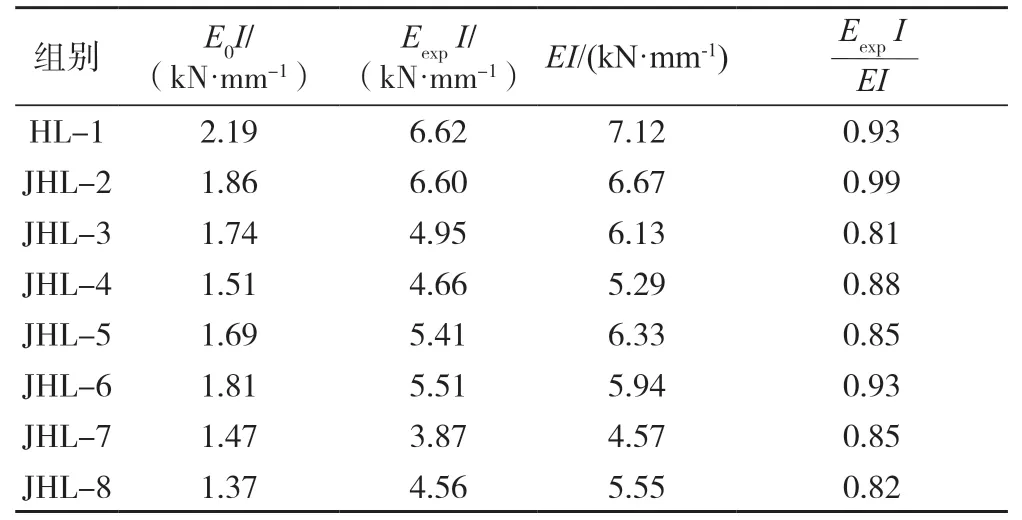
表3 初始弯曲刚度、试验弯曲刚度及理论弯曲刚度比较Tab.3 Comparison between initial bending stiffness, experimental bending stiffness and theoretical bending stiffness

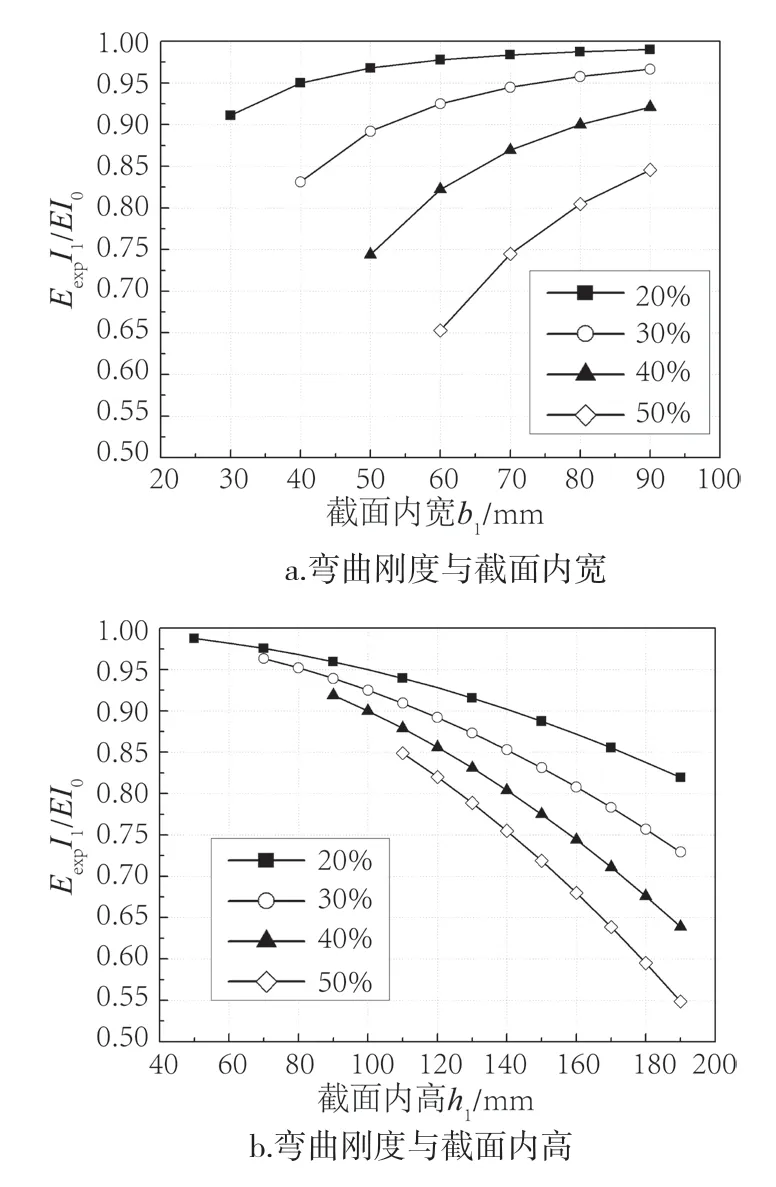
图8 空心部分尺寸与截面弯曲刚度的关系 Fig.8 Relationship between the hollow section size and bending stiffness

JHL-2 与JHL-5、JHL-4 与JHL-6、JHL-7 与JHL-8 这3 组空心梁试件相互间的空心率近似相同，但其初始刚度有差异，分别为10.1%、19.9%、7.3%；弯曲刚度差异分别为22%、18.2%、17.8%。因此可推测，试件空心率与初始刚度、弯曲刚度间无明显定量关系。而与HL-1 实心梁试件进行对比可知，JHL-2～8空心梁试件的初始弯曲刚度及试验弯曲刚度总体上随截面高度方向壁厚的减小而下降，而与截面宽度方向壁厚无明显关联性。不同空心率下，弯曲刚度随空心截面内宽、内高尺寸变化的关系如图8 所示，I1为空心截面惯性矩，I0为实心截面惯性矩。由图8a可知，空心率相同时，梁的弯曲刚度随截面内宽b1增加而增大，且空心率高、内宽较大时，刚度的增长趋势和速率更明显。由图8b可知，空心率相同时，梁的弯曲刚度随内高h1的增加而减小，且空心率越高减小速率越快。因此在工程设计中，当胶合木梁空心率一定时，应优先扩大空心部分内宽，使截面具有相对较高的弯曲刚度。

3 理论分析

3.1 变形计算

由试验结果可知，空心胶合木梁试验弯曲刚度小于理论弯曲刚度，使用弹性理论对其进行结构设计时，计算所得的挠度值或小于实际挠度变形，对结构而言不安全。因此，需对理论截面弯曲刚度进行折减，引入调整系数γ，则空心胶合木梁的有效弯曲刚度为：

式中： (EI )eff为空心胶合木梁的有效弯曲刚度，kN/mm； E为胶合木弹性模量，MPa；I为截面惯性矩，mm4；γ为调整系数，根据试验结果为0.88。

梁的跨中挠度按下式计算：

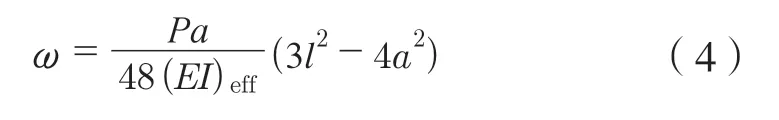
式中：ω为荷载P作用下的跨中挠度，mm；P为作用于梁的集中荷载，kN；l为梁的计算跨度，mm；a为加载点至支座的距离，mm；(EI )eff按式（3）计算，kN/mm。

根据式（4）计算得26%、33%、40%、52%空心率各组典型空心胶合木梁荷载-挠度曲线，与试验所得曲线比较见图9。由图可见，计算所得荷载-挠度曲线与试验曲线较吻合，且弹性阶段计算曲线值均小于试验曲线值，为结构设计预留了一定冗余度。因此，该计算空心胶合木梁挠度的方法可行。

图9 试件跨中挠度计算值与试验值对比 Fig.9 Comparison between the calculated and experimental deflection results

3.2 极限承载力计算

为研究小跨高比空心胶合木梁受弯试验的极限承载力，根据空心梁承载能力极限状态下的应力和应变分布，得计算简图，见图10，假设此时试件发生破坏。推导计算过程采用的假定条件：①梁截面应变分布符合平截面假定；②梁受拉及受压的弹模相同；③木材受压时视为理想弹塑性体，受拉时视为理想弹性体。

图10 空心梁截面计算简图Fig.10 Calculation sketch of hollow glulam beam section

由试验结果可知，空心梁截面高度方向壁厚t1与试件极限承载力、弯曲刚度等有较大关联性。空心胶合木梁的fte与fce的比值可表示为：

式中：fce为木纤维达极限弹性压应变时对应的应力，MPa；fte为下边缘木纤维达极限弹性拉应变对应的应力，MPa；h1为梁截面空心部分内高，mm；h为梁截面高度，mm。

因此，当截面空心率及宽度方向壁厚t2一定时，根据平衡关系有：

式中：Fp1、Fp2为空心梁塑性受压区分力，kN；Fc为空心梁弹性受压区合力，kN；Fte1、Fte2为空心梁受拉区分力，kN；b为空心梁截面宽度，mm；αh、βh、γh分别为空心梁塑性受压区高度、弹性受压区高度及受拉区高度，mm。

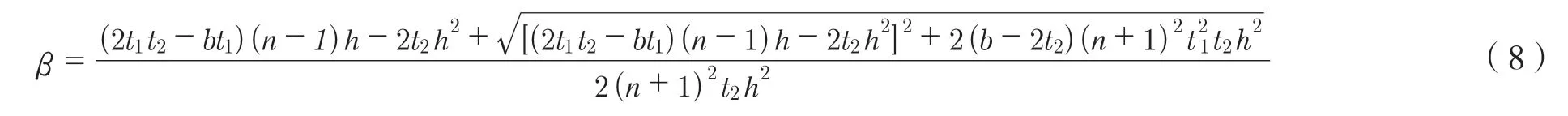
令 σ =(2t1t2-bt1)(n-1)h-2t2h2，代入式（8）得

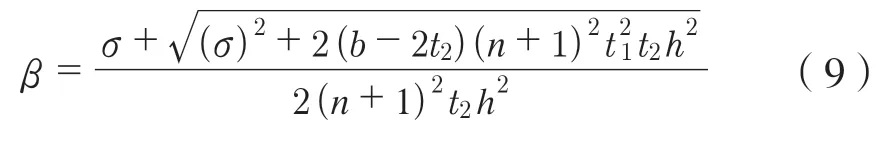
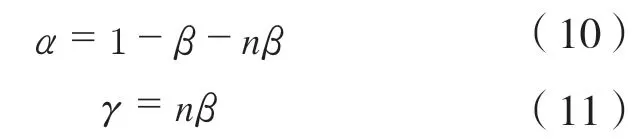
式中： εce、εte分别为空心梁最大弹性压应变、下边缘拉应变，με。

将各分力向中和轴取矩，得：

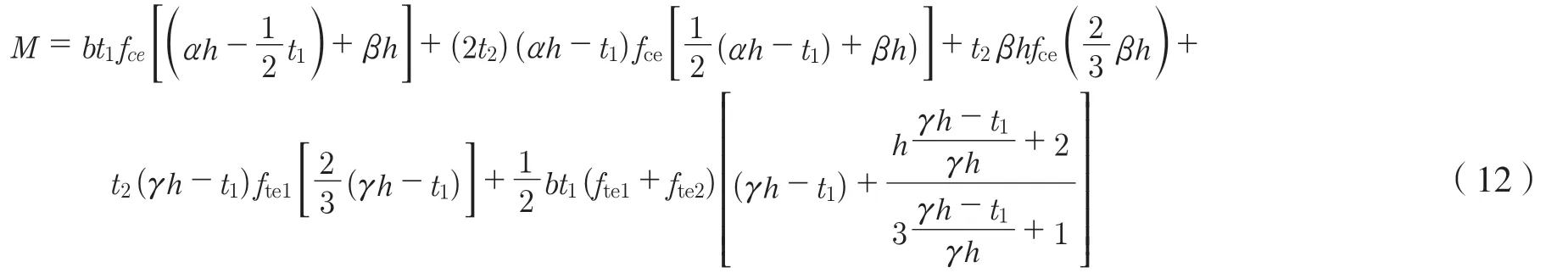
式中：M为空心梁的截面极限弯矩，kN·m。

3.3 剪切破坏形式判断

研究空心梁拉伸破坏和剪切破坏的界限，根据图10，空心梁破坏时中性轴区域发生剪切破坏，则有

式中：fv为胶合木材料顺纹剪切强度，MPa。

若发生剪切破坏，应符合εte2≤εteu，则

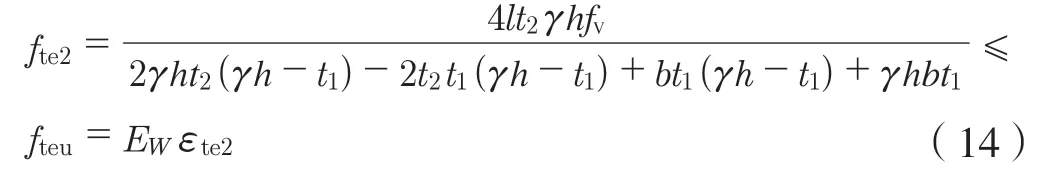
式中：εteu为空心梁极限拉应变，με；fteu为空心梁达极限拉应变对应的应力，MPa；Ew为胶合木材料弹性模量，MPa。

因此整理可得：

式（15）为三分点受弯试验时发生顺纹剪切破坏，梁截面高度方向壁厚与截面高度之比的界限。

4 结论

1）小跨高比空心胶合木梁破坏形式以梁底顺纹拉伸破坏为主；当截面宽度方向壁厚小于20 mm，空心率不小于52%时，则为发生于中性轴及偏下位置的剪切破坏形式，总体呈脆性破坏特征。空心梁截面壁厚不小于20 mm，空心率不大于40%时，其承载与变形能力满足结构设计要求。空心梁挠度最大值为跨度的1/67。

2）空心胶合木梁的极限承载力、延性与截面高度方向壁厚、空心率有关：壁厚越小，极限承载力及延性越小；空心率越小，极限承载力越大，延性越小。刚度与截面高度方向壁厚有关：壁厚越小，刚度越小。此外，当截面高度方向壁厚在20 ～50 mm，同时宽度方向壁厚在20 ～30 mm时，空心截面尺寸变化对梁底极限拉应变的影响较小。

3）空心胶合木梁的变形可使用弹性理论计算，进行弯曲刚度计算时需引入折减系数0.88。验证空心梁基本符合平截面假定后，提出空心梁极限承载力的计算方法，并计算了发生剪切破坏时截面高度方向壁厚与截面高度的界限。