锂电池异常状态监测的FEKF方法研究

朱浩，张潇

（湖南大学机械与运载工程学院，湖南长沙 410082）

得益于高能量密度、较高的电压平台以及较长的循环寿命[1]，锂离子电池已被广泛应用于各领域的能源系统中，但锂离子电池在使用过程中有可能出现过充、过放、温度过高、温度过低、电池老化等异常状态[2]，并由此引起电池损坏，甚至可能导致燃烧爆炸等安全性事故.因此，对锂离子电池工作时的异常状态进行监测是十分必要的.

Singh 等提出了使用卡尔曼滤波（Kalman Filter，KF）生成电池端电压残差，然后通过端电压残差的零点漂移的大小判断电池是否有故障的方法[3-4]，其中文献[3]使用一组不同的扩展卡尔曼滤波（Extended Kalman Filter，EKF）作为残差生成器，但EKF 遇到缓变型状态参数异常时可能在故障发生早期无法辨识甚至发散；文献[4]使用了改进的自适应无迹卡尔曼滤波（Adaptive Unscented Kalman Filter，AUKF）生成端电压残差，AUKF 能够更有效地辨识电池内阻R0与时间常数τ 的缓变故障.Chen 等通过递推最小二乘法（Recursive Least Square，RLS）与EKF 计算电池内阻R0、极化电阻Rp、极化电容Cp，然后得到这些参数的局部离群因子与故障诊断阈值，判断电池系统某单体电池电压的瞬时变化与持续异常变化，但如果遇到电池状态参数缓慢变化至超过设定阈值的情况，辨识参数可能在阈值范围上下波动，导致出现错误判断[5].Zhao 等引入渐消因子运用自适应扩展卡尔曼滤波（Adaptive Fading Extended Kalman Filter，AFEKF）对锂离子电池SOC 进行估算，实验证明渐消因子能够有效提高卡尔曼滤波的估算精度[6].Gao等使用基于遗传算法的神经网络对电池电压传感器、温度传感器、单体电池故障和电池内部短路故障进行了辨识，但该方法需要有大量优质的数据作为训练对象[7]；Ablay 等分别使用EKF 与龙伯格观测器（Luenberger Observers）生成电池内阻、极化电容电压与端电压的残差，并针对电压、温度传感器的故障做出测试，但是故障状态为软件仿真，没有实验验证[8-9].

显然，针对电池的基于端电压残差的故障诊断方法能够很直观地反映电池的运行状态.在系统处于正常状态时，端电压残差为0；当端电压残差出现较大的零点漂移时，表示电池状态参数出现异常.得益于其较小的计算量与较高的估算精度，EKF 成为使用最多的残差生成器，但是EKF 自适应性和跟踪性在面对各种不同的工况时无法满足需求，因此，本文使用递推最小二乘法对电池内部参数进行辨识，以获得状态空间中的未知参数R0、Rp、Cp；分别使用FEKF 和EKF 生成电池端路电压的残差，利用χ2检验获得异常状态判断阈值，并以低温异常状态为例，对方法进行实验验证.

1 锂离子电池建模

电池模型分为3 类：电化学模型、经验模型与等效电路模型.电化学模型根据电池内部的电化学反应建立，具有很高的精度，但计算复杂；经验模型主要依靠大量的数据，通过训练来达到较高的模型精度，对数据的数量和质量都有很高要求；等效电路模型使用电容电阻和恒压源等元器件构成电路来模拟电池的运作机理，结构简单且灵活，便于在线计算与仿真[10-13].由于锂离子电池内部结构可简化为欧姆内阻和极化内阻，且一阶模型的精度已经能够满足需求，因此采用一阶RC 等效电路模型来模拟锂离子电池内部结构，等效电路如图1 所示.

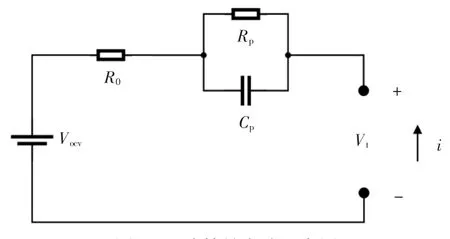
图1 一阶等效电路示意图Fig.1 First-order equivalent circuit diagram

根据基尔霍夫电压定律，可得到关系式：

电池的SOC 可表示为：

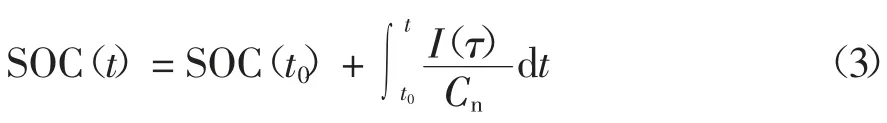
经过离散化后，式（3）可变为：

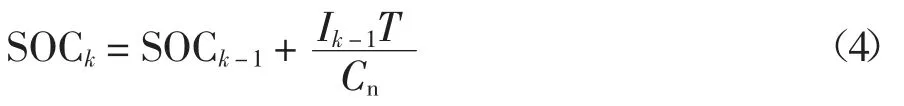
式中：t0为充放电的开始时刻；Cn为电池容量；T 为采样周期；Rp为电池极化电阻；Cp为电池极化电容；I为电池工作电流；Vp为极化电容上的电压；Vocv为电池开路电压；R0为电池内阻；Vt为电池端电压.开路电压Vocv与电池SOC 之间的关系可以通过对充放电实验的数据进行曲线拟合得到.

2 FEKF 滤波

EKF 在初始条件选取得当的情况下，能够得到比较准确的状态估计值，但是任何一个实际系统都具有一定程度的不确定性，此时的EKF 滤波精度可能会下降甚至发散.为了克服这一缺点，引入渐消因子.

2.1 状态参数辨识

使用RLS 对电池的欧姆内阻R0、极化电阻Rp、极化电容Cp进行在线辨识[14].该系统的离散数学模型为：

式中：zk为系统输出；μ 为前一时刻的输入输出向量，令μ=，Ik，Ik-1]；θ0为系统真实状态参数的代换向量，用以表示待辨识的状态参数：电池内阻R0、极化电阻Rp和极化电容Cp.RLS 的递推公式表达为：

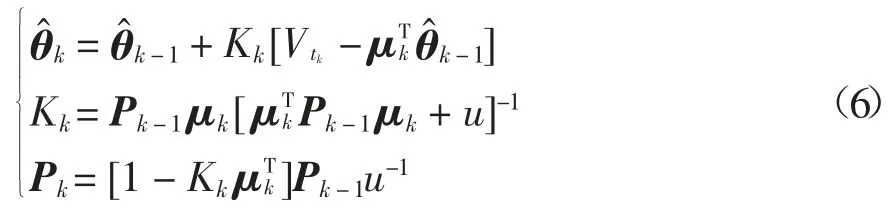
式中：K 为增益因子；P 为协方差矩阵；u 为遗忘因子；θ 为系统参数估计值向量，维度与μ 相同.u 越小跟踪能力越强，但波动也越大，一般取0.95 ＜u ＜1，为保证参数辨识的准确性与稳定性，取中间值，令u=0.985.

首先进行参数初始化，令μ、θ、K 的初始值均为0，P 的初始值则通过多次调试得到，为I1×3×106，I 为单位矩阵；然后将充放电过程中的V 与I 分别代入式（6），即可得到每一时刻的θ 值，完成参数辨识.

2.2 状态方程确立

在早期，电池状态参数的偏差通常较小，由于EKF 与UKF 的鲁棒性较差，不易被系统模型识别，造成监测诊断的延迟.因此，引入时变渐消因子λk.当系统模型存在不确定性时，会首先在端电压残差序列rk中表现出来，导致≠0，即输出端电压残差序列不正交.此时，通过渐消因子λk在线实时调整增益矩阵Kk，可以保证EKF 的输出端电压残差序列相互正交，从而使EKF 具有强跟踪滤波器的性质.由于状态方程变量为一维，计算量很小，所以采用最优渐消因子.

设状态方程变量xk=SOCk，系统状态和观测方程可表示为：

式中：w 和v 是均值为0、方差分别为q 和r 的不相关高斯白噪声.通过式（4），可以得到g 的表达式：

通过式（1）（2）可以得到h 的表达式：

引入渐消因子λk，令λ1=1，其它的渐消因子可由式（11）得到：

式中：φ ＞0 为迭代步长，取值要求λk能够快速衰减，而的计算方法为：

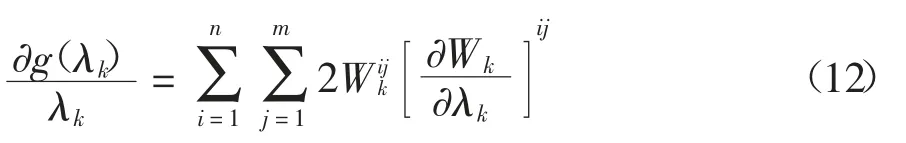
至此可得到卡尔曼滤波的预测方程：

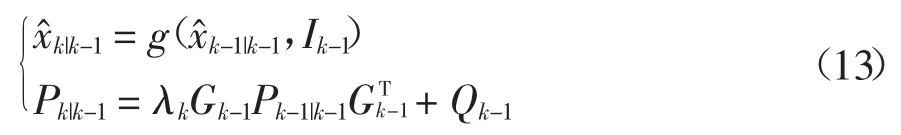
迭代方程由式（14）表达：

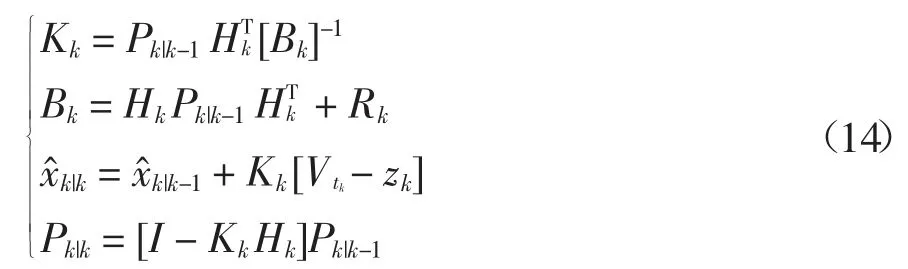
式中:G 和H 分别为非线性函数g 与h 的一阶Taylor展开，即得到端电压残差值为rk=-zk.

3 状态参数异常阈值计算

当电池状态出现异常时，其状态参数会出现变化，由此引起放电过程中端电压残差出现零点漂移，因此可用端电压残差数据的变化作为状态参数异常判断的依据.

影响状态参数异常阈值η 的决定性因素为误检率PFA和漏检率PM.若设定阈值较高，则漏检率随之升高，而误检率随之降低；若设定阈值较低，则情况相反[15].构造检测函数为：

式中：Tk为端电压残差序列的方差Rk.由于残差序列为符合高斯分布的白噪声，所以Dk符合χ2分布.取滑动窗口宽度为A，将窗口宽度内采样点Dk的平均值作为判断该窗口内数据是否出现状态参数异常的依据，即，依此得到误检率PFA的计算式[16-18]：

式中：η 为状态参数异常阈值.可通过初步设定PFA的值得到阈值大小.本系统中χ2分布的自由度为1，则对应不同误检率的状态参数异常阈值等同于χ2分布临界值，如表1 所示.

表1 误检率分布表Tab.1 False detection rate distribution

当滑动窗口内检测函数ηk大于η 时，判断为系统状态参数异常，否则系统状态参数正常.判断逻辑为：

4 实验设计与数据分析

为了模拟缓变型状态参数异常，将电池置入恒温恒湿箱中缓慢降温，在动态应力测试工况（Dynamic Stress Test，DST）下进行放电循环.电池为亿纬锂能公司容量为2.55 Ah 的18650 型号三元锂电池，充放电截止电压分别为4.2 V 与2.75 V；恒温箱为泓进仪器HY-1010 型；充放电机为德普BTS20-5V/4×200A.实验平台原理图如图2 所示.

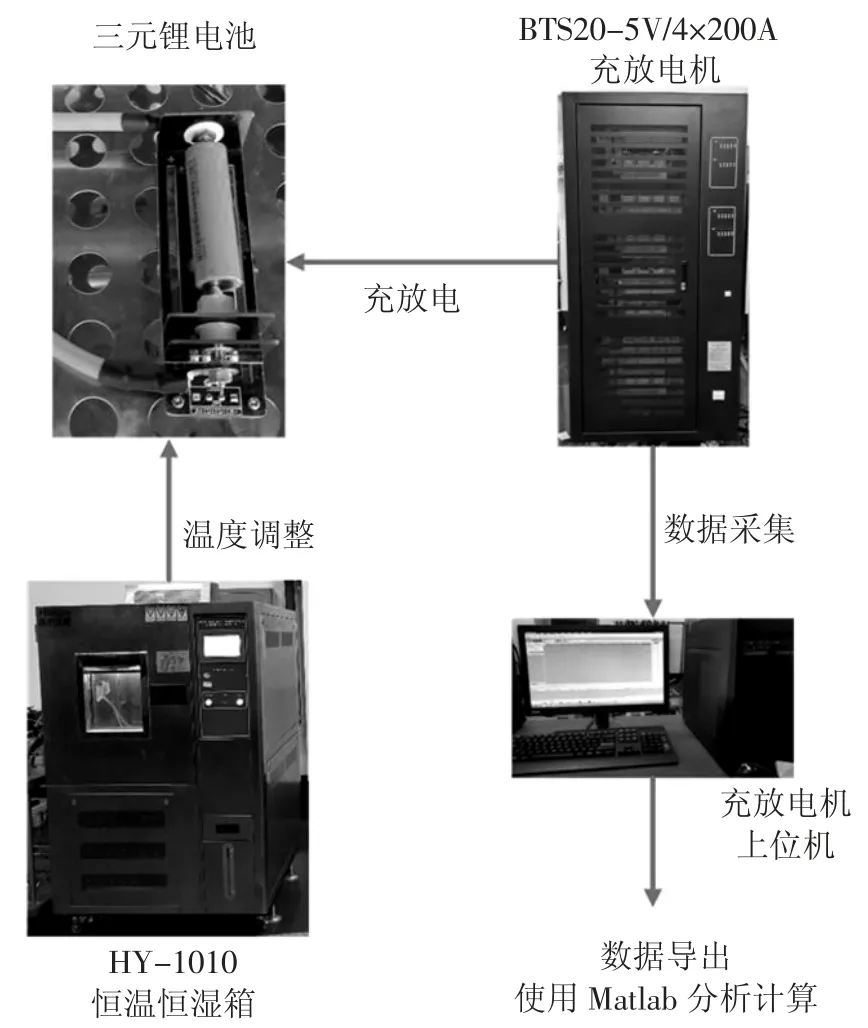
图2 充放电实验平台Fig.2 Charge and discharge experiment platform

首先需要得到电池的OCV-SOC 曲线.在25 ℃时，电池充满至4.2 V 截止电压的情况下，对电池进行恒流放电实验，三元锂电池的最大持续放电电流倍率为3 C，为了保证实验安全取较小的放电电流倍率0.5 C，放电至电压低于2.75 V，采样周期为1 s，实验测得OCV-SOC 曲线如图3 所示.

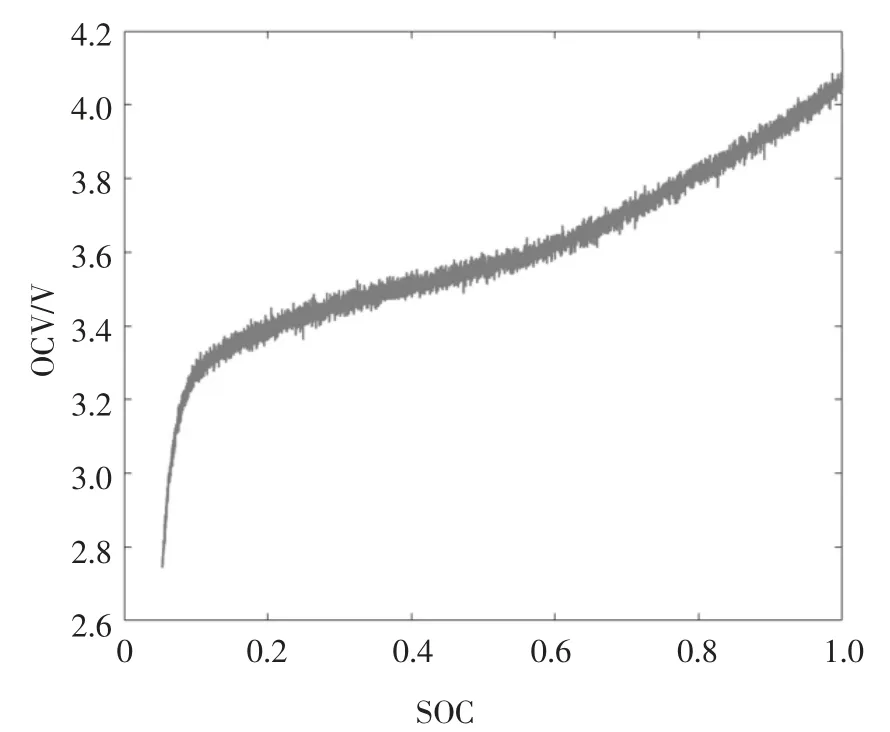
图3 OCV-SOC 曲线Fig.3 OCV-SOC curve

Matlab 的函数拟合方法主要包括插值拟合、多项式拟合与局部加权回归拟合，其中多项式拟合可以通过调整阶数防止出现过拟合与欠拟合的情况，并且多项式结构简洁、易于表达.经过调试，最终以七阶多项式拟合得到OCV-SOC 对应关系的多项式：

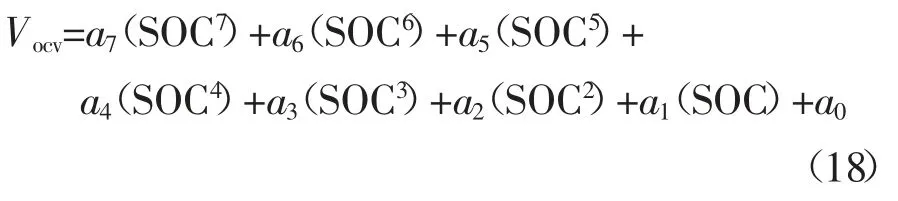
式中：a7=-20.49，a6=74.31，a5=-106，a4=73.23，a3=-23.36，a2=2.453，a1=0.585 9，a0=0.344 5.

然后将单体电池置入恒温恒湿箱，将恒温恒湿箱内温度稳定至室温25 ℃，开始进行放电；1 h 后开始降温，约在25 min 后降至5 ℃，5 min 后缓慢回温至25 ℃，直至放电结束.期间温度变化曲线如图4所示，DST 放电循环的电流曲线如图5 所示，充放电机的采样周期为1 s，图5 所示的1 000 个采样点中包括两个循环周期.

实验结束后，使用Matlab 做数据处理：

1）将上位机采集到的实时电流电压数据导入脚本文件，先通过递推最小二乘法计算得到正常的电池状态参数R0、Rp、Cp，时间常数τ=RpCp.

2）将辨识出来的状态参数与上位机采集到的电池端电压与电流代入FEKF 计算，得到25 ℃降温到5 ℃过程中的SOC 估算值以及端电压残差值r，并使用电池容量Cn减去每一时刻的电流与时间乘积，得到安时积分的SOC 真实值；所用到的Cn由实验平台的充放电机直接测算得到，为2.469 Ah，温度变化的影响已被计算在内.

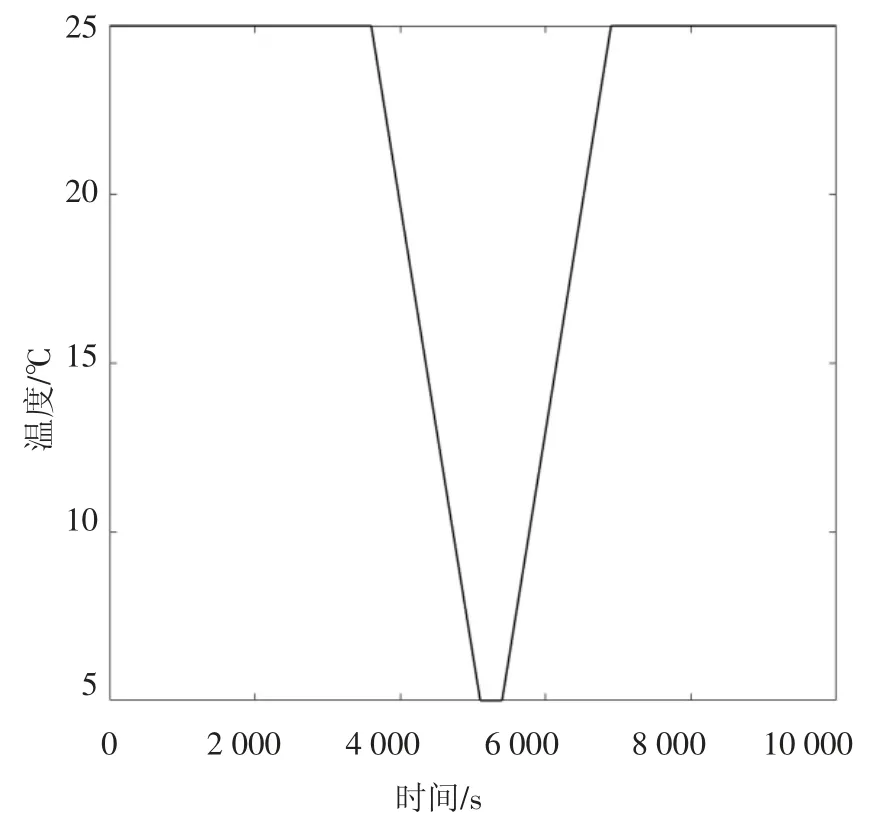
图4 温度变化曲线Fig.4 Temperature change curve

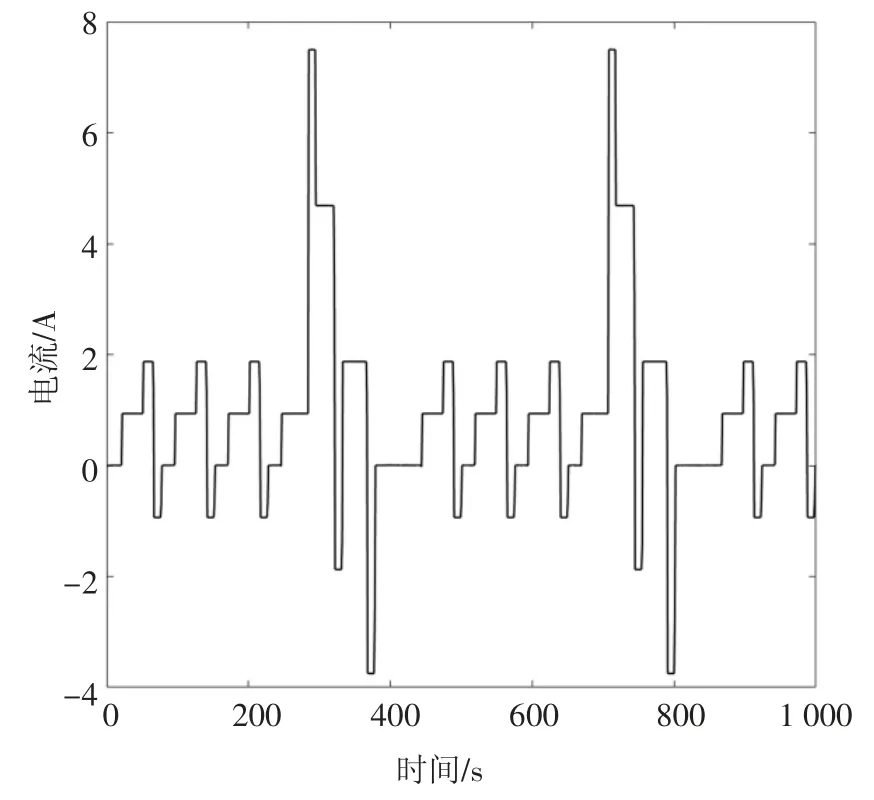
图5 DST 放电电流曲线Fig.5 DST discharge current curve

3）将端电压残差r 变换为χ2分布的Dk，取温度降低到5 ℃后的1 500 s，即5 000～6 500 s 采样点的Dk进行对比.

不同算法下，Dk的变化分别如图6、图7 所示；不同工况下不同算法的SOC 估算值与实际值分别如图7～10 所示.

从图6、图7 的对比可知，温度降低至5 ℃后，端电压残差参数Dk在逐渐增大，在6 200 s 后达到峰值，但是通过EKF 生成的数据在6 200 s 前波动幅值不大，无法在较早的时间检测出系统参数异常；而FEKF 生成的端电压残差数据Dk从5 700 s 开始便出现较大幅值的波动，能够更及时地检测出参数的异常.显然，渐消因子的引入有效增大了异常状态下的端电压残差，且未对正常状态下的端电压残差造成影响.

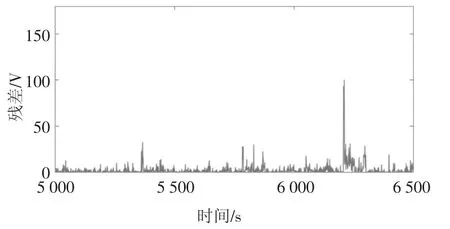
图6 降温流程结束时EKF 生成的不同时刻残差参数DkFig.6 Residual parameter Dk at different times generated by EKF at the end of the cooling process

图7 降温流程结束时FEKF 生成的不同时刻残差参数DkFig.7 Residual parameter Dk at different times generated by FEKF at the end of the cooling process

在温度降至最低5 ℃的时刻约5 000 s 时，由于锂离子电池在不同温度下的扩散作用的差异，电池的时间常数τ 与内阻R0缓慢增大[19]，根据式（1）（2）（14），在电池容量与电流大小不变的情况下，端电压残差会随之增大，SOC 估算值随之减小.因此，在温度由25 ℃降低到5 ℃后，EKF 对SOC 的估算精度开始下降，逐渐偏离由安时积分计算得到的真实SOC曲线，如图8 所示；而得益于渐消因子的引入，使用FEKF 进行估算得到的SOC 与真实值之间的偏差很小，如图9 所示，证明FEKF 在放大端电压残差的同时精度几乎未受影响.

分别取滑动窗口宽度A1=100，A2=50.取状态参数异常阈值η=3.84，根据表1，此时误检率PFA=5%.每Ak个点为一组，计算每组Dk的平均值若大于η，则认为Ak窗口宽度内，电池出现状态参数异常，否则正常.取采样时间为5 000～6 500 s，实时监测结果如图10～13 所示，概率为1 表示检测结果为状态参数异常，概率为0 则表示检测结果为状态参数正常.

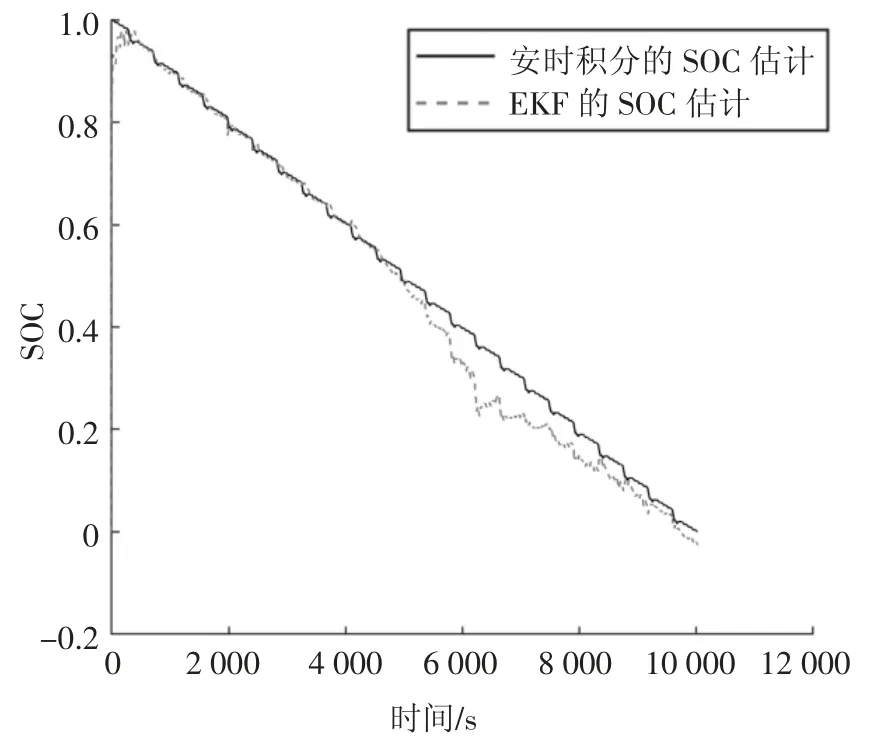
图8 25 ℃降温至5 ℃过程中使用EKF 的SOC 估算Fig.8 SOC estimation using EKF during cooling from 25 ℃to 5 ℃

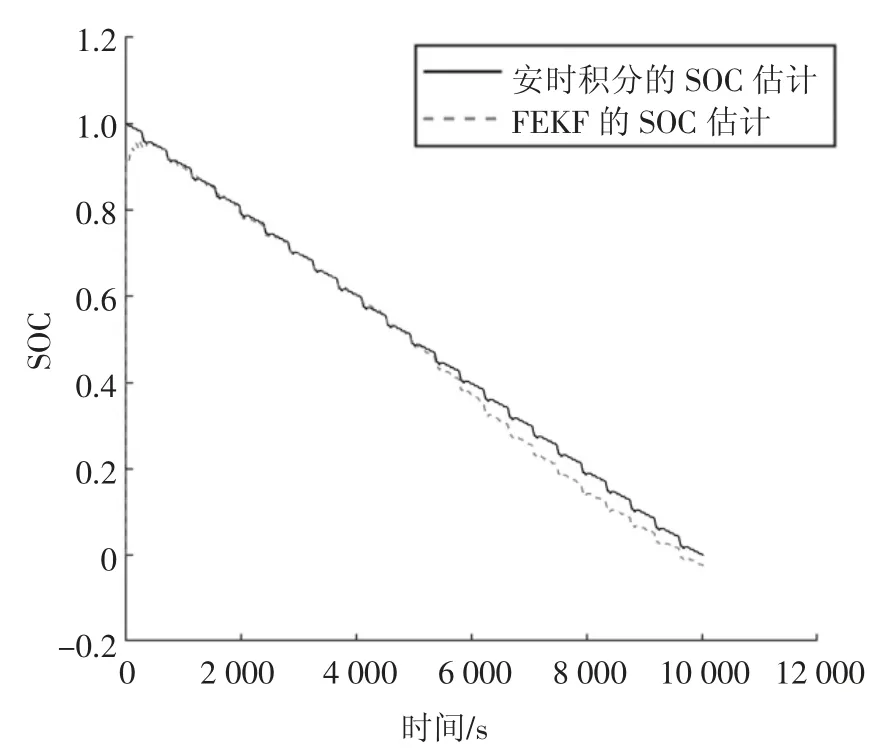
图9 25 ℃降温至5 ℃过程中使用FEKF 的SOC 估算Fig.9 SOC estimation using FEKF during cooling from 25 ℃to 5 ℃

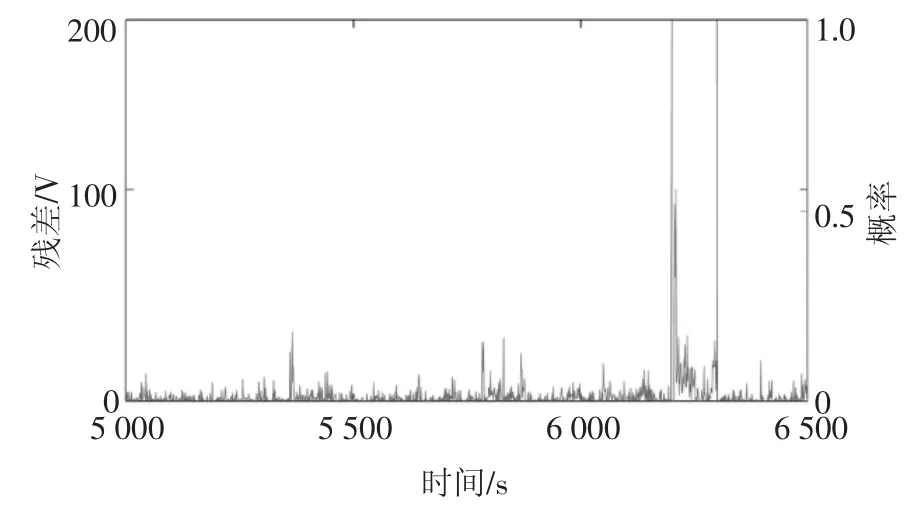
图10 滑动窗口宽度为100 时EKF 生成残差的状态监测结果Fig.10 Condition monitoring results of residuals generated by EKF when the data window width is 100

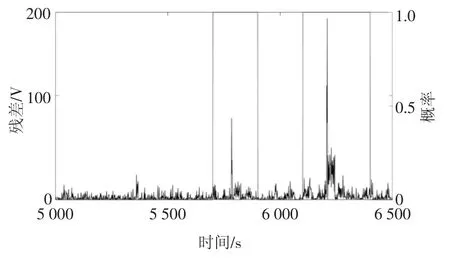
图11 滑动窗口宽度为100 时FEKF 生成残差的状态监测结果Fig.11 Condition monitoring results of residuals generated by FEKF when the data window width is 100

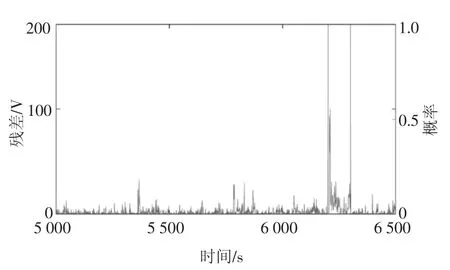
图12 滑动窗口宽度为50 时EKF生成残差的状态监测结果Fig.12 Condition monitoring results of residuals generated by EKF when the data window width is 50

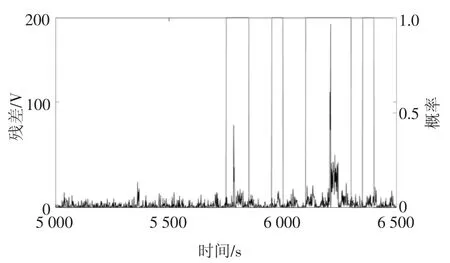
图13 滑动窗口宽度为50 时FEKF 生成残差的状态监测结果Fig.13 Condition monitoring results of residuals generated by FEKF when the data window width is 50

从图10、图11 的对比可知，在A=100 时，使用EKF 生成的残差只在6 200～6 300 s 内出现大于阈值的偏移，而使用FEKF 生成的残差在5 700～5 900 s、6 100～6 400 s 内出现大于阈值的偏移；根据图12、图13，在A=50 时，使用EKF 生成的残差在6 200～6 300 s 内出现大于阈值的偏移，而FEKF生成的残差分别在5 700～5 800 s、5 950～6 000 s、6 100～6 300 s、6 350～6 400 s 内出现大于阈值的偏移.很显然，使用EKF 得到的结果在6 200 s 才诊断出电池状态参数异常，告警只维持了100 s；而使用FEKF 得到的结果，最早在5 700 s 便诊断出电池状态参数异常，且在之后的600 s 内持续告警.因此，使用FEKF 生成的残差诊断出电池异常状态的时间更早，告警持续时间更长，较之EKF 有更好的监测性能.

5 结论

1）针对传统EKF 无法及时识别锂电池工作过程中出现的缓变型状态参数异常的问题，提出了加入最优渐消因子的FEKF，通过FEKF 生成残差，构造了χ2分布数列来计算误检率PFA以及对应的状态参数异常阈值η.

2）将单体电池置于恒温恒湿箱进行缓慢降温，按设置的工况，通过实验测得了电池的电流电压数据，将数据导入Matlab 的算法程序中进行计算，得到EKF 与FEKF 两种不同算法下实时监测的情况.证明了在相同的滑动窗口宽度以及阈值下，FEKF 相较传统EKF 能够更及时地识别出锂电池运行时出现的缓变型状态异常.