基于双层场景约简的电力系统灵活性规划方法
柴国峰,杨修宇,徐唐海,徐铭宏,柴仁勇
(1.现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学),吉林 吉林 132012;2.国网江西省电力公司景德镇供电分公司,江西 景德镇 333000;3.国网赣西供电公司,江西 新余 338025)
大力发展可再生能源RE(Renewable Energy,RE)是全球应对能源危机和气候变化的重要举措.全世界各国纷纷制定了2050年RE高占比的伟大发展蓝图[1-3].其中风力发电是重要可再生能源之一,近年来风电快速发展年增长率在10%以上,同时弃风率高居不下,15-16年我国平均弃风率高达15%和17%.电力系统灵活性不足是弃风的主要原因之一,因此,研究电力系统灵活性专项规划方法,对未来实现低碳化能源转型具有重要的现实意义[4].
随着RE占比的不断升高,系统灵活性调节能力不足的问题日益凸显,电力系统灵活性相关研究也逐渐成为热点.关于电力系统灵活性概念与评价指标开展了系列研究[5-12].其中,文献[7-8]先后从功率调节范围角度、爬坡速率角度对系统内各类灵活性资源进行了定量分析.文献[9]从调度运行角度提出了含有10个灵活性评价指标的评估方法.文献[10-11]建立了概率型的灵活性指标评价体系.而关于电力系统灵活性规划方面研究较少[13-14].文献[13]给出了灵活性资源供给与灵活性需求之间平衡机理并构建了含有资源投资决策与运行模拟的源荷储一体化双层优化模型.文献[14]在风电接入情况下,对中断负荷与储能等灵活性资源进行规划.文献[15-16]利用电转气(P2G)技术提升系统灵活性,解决RE消纳问题.文献[17]针对未来高比例可再生能目标,进行了考虑了源荷储多类型灵活性资源的中长期电源规划.从上述研究中可知电力系统灵活性规划依赖RE与负荷的时序模拟,若全年时序模拟则寻优过程计算量巨大,而如上述文献中采用直接给出典型日场景,则计算结果精度很难保证.
场景约简(即多场景分析法)是缩小搜索空间,提升寻优效率的有效方法,该方法是利用多个确定性场景及其场景概率表征RE出力的不确定性.虽多场景分析法已有大量研究,多是聚焦于输电网规划领域中可再生源出力不确定性表达,主要方法有区间法[18-19]、随机模拟法[20](拉丁超立方、蒙特卡洛模拟)以及最为常用的聚类方法[21-24].但这些方法会在场景约简过程中遗失很多重要的规划时序信息,这样会使规划结果的灵活性资源配置不足,造成严重弃风、弃光问题.
综上所述,本文从风电与负荷时序作用关系分析入手,依据两者不同时序作用关系对灵活性需求影响不同,构建基于K-means双层场景约简方法,并通过实测数据验证了场景约简的有效性.在此基础上,建立了针对火电机组灵活性改造与储能的含建设成本与运行成本的灵活性资源电源优化配置模型;最后通过对东北某电网风电、负荷的实测数据算例分析,验证了本文方法的有效性与实用性.
1 双层场景约简方法
1.1 RE与负荷时序关系对灵活性供需的影响
RE、负荷的出力均具有较强的间歇性与不确定性,两者在时序上的作用关系决定了电力系统灵活性需求.本文以日为时间尺度分析风电接入前后灵活性供需的变化.
风电接入前每日常规机组开机容量是以净负荷最大值并留有一定备用制定的,灵活性供给由常规机组提供,而灵活性需求由负荷决定,如公式(1)所示.
(1)
而风电接入后常规机组开机容量将降低,按最大负荷减去风电置信度或净负荷最大值,灵活性需求由净负荷决定,如公式(2)所示.
(2)
若风电波动的幅值以及与负荷波动是否一致,将直接影响系统的灵活性需求.因此,本文依据风电与负荷相互作用关系,将365日场景划分为3类不同系统灵活性供需的典型场景:正向型、反向型以及过向型,如图1所示.
正向型:风电功率幅值小且与负荷时序变化基本一致,即同增同降,进而风电接入后系统灵活性需求减小或不变;
反向型:风电功率与负荷时序变化趋势相反,即一增一降,风电接入后净负荷峰谷差增大,进而增加了系统灵活性需求;
过向型:风电功率幅值大且与负荷时序变化基本一致,但由于风电幅值过大,使净负荷峰谷差增大,同样增大了系统灵活性需求.
由此可见,三类典型场景主要由风电与负荷的时序趋势与接入风电后净负荷灵活性需求的增减加以区分.因此,本文利用第i日的风电功率与负荷功率的相关系数来描述两者时序变化一致程度;利用第i日的负荷峰谷差与净负荷峰谷差的差值刻画峰谷差变化程度.
(3)
(4)
Cr,i=sgn[max(rL&W,i,0)×sgn(ΔPreq,max-i)],
(5)

1.2 双层场景约简方法
通过1.1分析可知,风电功率幅值大小以及与负荷时序上变化一致性将决定系统的灵活性需求.因此,在场景约简时如何避免遗失负荷与风电之间的时序变化关系是需要研究的工作.本文提出的双层结构场景约简方法,第一层充分考虑了风电、负荷之间时序作用关系,并基于不同关系进行分类;第二层在第一层基础上进行场景约简.具体操作步骤为:首先,以日调度周期为时间尺度输出风电功率与负荷数据;然后,根据风电与负荷之间的作用关系,利用相关性系数以及灵活性需求变化将365场景划分为:正向型、反向型和过向型三类;最后,利用K-means聚类算法对场景进行削减,具体流程如图2所示.

1.3 场景约简方法的灵活性评价指标
为了校验双层聚类场景约简的有效性,本文提出了平均灵活性需求变化ΔPA,req与灵活性不足期望(Loss of Flexibility Expectation,LOFE)两个评价指标.
(1)平均灵活性需求变化ΔPA,req
为了能够从全年时间尺度上评价风电接入对系统灵活性总体改变情况,将所有场景的灵活性需求变化量进行取平均值,即
(7)
公式中:T总场景数.
(2)灵活性不足期望LOFE
在明确了需求变化程度后,另一重要的信息就是系统灵活性不足的程度.由此进一步引入系统的灵活性不足期望LOFE为i调度场景内系统灵活性最大供给不能满足灵活性最大需求的平均值,其能够反映系统灵活性供需的情况.
(8)
2 电力系统灵活性优化配置模型
本文灵活性资源主要为火电机组灵活性改造与储能装置,不考虑需求侧响应,且假设电网无阻塞、过载,仅在电源侧考虑灵活性供需平衡.其中,火电机组灵活性改造主要通过减少火电最小技术出力来为系统提供下调灵活性资源;储能是利用自身对于能量的吞吐特性,实现能量的时移,从而为系统提供灵活性.灵活性资源优化配置与弃风损失的关系为:系统灵活性供给不足将造成弃风,而火电机组灵活性改造与储能都能够提升了风电的消纳空间,减小弃风,因此弃风损失与灵活性投入成本存在优化关系.但两者经济性与作用方式不同,火电机组改造能够长期增加系统下调灵活性供给,适用于弃风持续时间长的场景;而储能适用于持续时间短的弃风.
2.1 目标函数
综合考虑灵活性资源建设成本与弃风惩罚、燃煤等系统运行成本,构建火电机组灵活性改造与储能之间协调优化配置模型,目标函数为.
Foverall=min(FInv+Foper),
(9)
公式中:Foverall为总成本;FInv代表灵活性资源建设成本;Foper为运行成本.其中,FInv包括火电灵活性改造成本、储能成本.
(10)
公式中:Ng为火电机组台数;Ith为火电机组改造单位容量成本;Cth,g为g台火电机组改造容量;Z为第g台火电机组改造的0-1决策变量;Iess,p为储能装置变流器单位功率造价;Iess,C为储能装置单位容量成本;Pess、Cess分别为储能装置的功率与容量.系统的总运行成本Foper包括储能运行成本、弃风损失以及火电发电成本.这里储能运行成本是由于储能充放电效率造成的电量损耗成本,按照煤电成本计算,且不计火电机组启停成本,则运行成本公式如下:

(11)
2.2 约束条件
2.2.1 灵活性资源建设决策约束
(1)火电机组改造深度约束
0≤Cth,g≤Cth,max-g,
(12)
公式中:Cth,max-g为火电机组g的灵活性改造上限.
(2)储能装置建设容量约束,本文并未设置储能容量配置上限,认为主要由经济决定.
2.2.2 运行约束
(1)火电机组出力上下限约束
Pmin-g≤Pg(t)≤Pmax-g,
(13)
公式中:Pg(t)、Pmin-g、Pmax-g分别为火电机组出力,火电机组出力上,改造后火电机组出力下限.
(2)火电机组深度改造与出力下限耦合关系
Pmin-g=Pold,min-g-Cth.g,
(14)
公式中:Pold,min-g改造之前火电机组的出力下限.
(3)储能装置运行约束
-Pess.max-in≤Pess(t)≤Pess.max-out,
(15)
(16)
公式(15)为储能充放电功率约束,其中Pess(t)、Pess.max-in、Pess.max-out分布为t时刻储能装置注入功率,充电功率极限约束、放电功率极限约束;公式(16)为储能充放电量约束,其中SOC(t)、SOCmin、SOCmin分别为t时刻的储能荷电状态、储能荷电状态上限和下限.
(4)有功功率实时平衡约束
在考虑灵活性的规划中,功率平衡约束除了要包含火电出力、风电出力、弃风和负荷需求以外,还要增加与储能的运行情况的考虑,如公式(17)所示.
(17)
(5)支路潮流约束
(18)
(19)
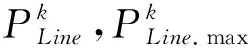
3 算例分析
3.1 基础数据
本文以东北某地区电网实测负荷与风电功率数据作为分析对象,其中数据采样时间尺度为1点/h,负荷最大值为1 946 MW,风电装机容量1900 MW.常规火电机组装机共为2 200 MW,其中包括:200 MW机组2台、300 MW机组4台、600 MW机组1台,各类型机组初始最小技术出力为装机容量的55%,而改造上限为装机容量的40%.结合IEEE30算例系统进行仿真验证,在12节点与16节点分别接入1 000 MW与900 MW的风电装机,并按照容量大小配置相应比例的储能.计算条件如表1所示.

表1 计算条件
3.2 场景约简及校验
利用本文提出的双层聚类方法与常用K-means聚类方法对给出的实测数据进行聚类(详细数据见附录Ⅰ中,附图(1)),得出相应的典型场景,并对两类场景进行量化的对比分析.
(1)双层约简典型场景
根据式(3-5)计算判断得到出:正向型有37天反向型有206天,过向型有122天,进而将各类型数据进行K-means取得典型场景.
为了消除由于聚类数对两种方法场景的影响,本文将两种方法的聚类数统一为20类.在双层约简各类型的聚类数由其全年占比决定.图(3)为双层约简的典型场景.双层约简方法每类典型场景的全年占比详见附录Ⅰ,附表(1).
(2)K-means典型场景
K-means聚类的取得典型场景,聚类数为20.K-means聚类方法的典型场景和每类典型场景的全年占比详见附录Ⅰ,附图(2)和附表(2).
(3)双层约简、K-means典型场景量化分析
以系统平均灵活性需求变化以及系统灵活性不足期望作为场景约减有效性校验指标.分别对比本文提出的双层场景约简、常规K-means聚类与原始数据等指标变化情况,从而校验本文场景约减有效性,具体指标如表2所示.

表2 场景约简前后灵活性评价指标对比标
从表1对比可知,本文提出的双层聚类方法从系统最大灵活性需求变化ΔPA,req、系统灵活性不足期望LOFE两方面都更加接近实际值,说明双层聚类能够一定程度保留风电与负荷时序关系.
3.3 灵活性资源优化配置结果
根据3.2聚类分析的典型场景数据,结合本文提出的灵活性资源优化配置模型进行优化,其中将灵活性资源步长设置为10 MW.为了对比本文提出的双层聚类方法的优劣,利用含有时序模拟的场景分析法对本文建立的优化模型进行求解并进行生产模拟比较两种方法的优劣,优化结果如表3所示.
通过表3对比结果可知,本文提出的双层聚类方法较常用K-means聚类方法在灵活性资源配置方案中,火电改造容量多了210 MW,储能容量配置少了11 MW·h;但在生产模拟中,综合成本少了3.58亿元,弃风电量少了1.79×105MW·h,弃风率减少了4.96%.由此可见,双层聚类方法能够更好地保留负荷与风电的时序作用关系,规划方案可靠性相对常规聚类方法更高.另一方面,由于目前储能成本较高,所以在当下的灵活性配置成本下,火电改造在应对灵活性需求方面更加经济适用.

表3 优化配置结果
为了进一步说明本文方法有效性,在灵活性资源最优配置方案下,给出三类型典型场景的灵活性资源工作时序加以分析.正、反、过等三个典型场景灵活性资源工作时序图,如图4所示.其中,正向型:火电灵活性改造就可以提供充足的灵活性;反向型:由于灵活性需求量较大与经济性原因,火电灵活性改造与储能配置结合仍不能完全满足灵活性需求,存在少量弃风;过向型:火电改造加上储能配置就能满足灵活性需求.
近年来储能的技术、经济性持续改善,为了分析储能技术发展对灵活性资源优化配置的影响,现将储能成本以25万元/MW·h为步长下降,优化配置的影响如图5所示.
图5可见,随着储能成本的下降,优化配置中火电改造容量不断降低,储能容量配置不断升高,弃风量不断下降.可见在储能成本降低的情况下,不仅储能装置适应性会明显提高,而且会更好的减少弃风.
4 结 论
本文针对在电力系统灵活性资源规划中聚类方式的场景约简易造成时序信息大量流失问题,提出了基于K-means的双层结构场景约减方法,实现了大量保留可再生能源与负荷时序关系的场景约简;在此基础上,构建了综合考虑灵活性资源建设成本与系统运行成本的火电改造与储能的协调优化配置模型,并通过东北某地区实测数据分析对比,验证了所提出方法的有效性.主要结论如下:
(1)本文双层场景聚类方法与常规K-means方法对比,在系统最大灵活性需求变化ΔPA,req和系统灵活性不足期望LOFE两方面都更加接近实际值(ΔPA,req:实际值280.8、本文方法171.1、常规K-means159.7;LOFE:实际值652.8、本文方法615.1、常规K-means609.4),因此本文提出的双层聚类方法能够保留两者时序信息.
(2)本文构建了综合考虑灵活性资源建设成本、系统运行成本的灵活性资源优化配置模型,实现多类型灵活性资源之间优化配置.同时在双层聚类方法与常规K-means给定场景进行灵活性资源配置,双层聚类方法综合成本方面较常规K-means节约资金3.58亿元约9%、弃风率降低了4.96%,进一步验证了双层聚类的有效性.
(3)随着储能技术持续发展、成本的进一步下降,其将成为未来高比例可再生能源电力系统中的重要关键技术之一,未来应用前景广阔.
附录1
1.基本风电、负荷数据
2.K-means聚类典型场景
3.双层约简、K-means聚类典型场景发生概率

附表2 K-means各典型场景的发生概率

