基于小波和贝叶斯网络的智能建筑供配电系统故障诊断研究

刘晓琴，王晨旭，孙海军，王 千

（1.辽宁石油化工大学信息与控制工程学院，辽宁抚顺113001；2.辽宁石油化工大学石油化工过程控制国家级实验教学示范中心，辽宁 抚顺113001；3.中国石油抚顺石化公司 热电厂，辽宁 抚顺113008）

当前，智能建筑供配电系统的可靠性和安全性已成为百姓关注的焦点和热点[1-2]。智能建筑供配电系统日益庞大，不可避免会出现故障，一旦发生故障，势必会影响到居民的正常生活，经济损失严重，甚至会造成人身伤亡事故[3]。因此，智能建筑中供配电系统的故障诊断技术显得尤为重要。

国内外相关科研人员研究出多种供配电网络的故障诊断方法。文献[4-5]提出利用神经网络算法对电网进行故障诊断，其容错和抗干扰能力强，故障诊断速度快。但是进行故障诊断时，需要大量的故障特征学习样本，会导致学习训练收敛速度慢；此外，该方法缺乏对电网故障诊断结果解释能力。文献[6-7]提出petri 网络供配电网故障诊断方法，该方法得到的故障诊断结果具有较强的直观性，但不适用复杂的电网拓扑，而且抗干扰和容错能力差，诊断结果精确度有待提高。文献[8]结合粗糙集理论对供配电系统进行故障诊断，该方法在处理供配电网络故障诊断中不确定、不完善、不精准的故障信息方面具有突出的优势。但是，应用于大规模电网故障诊断时，网络矩阵维数多，满足不了在线诊断的需求。文献[9-15]核心思想是将复杂的电网数学模型转化为简单的“0-1”规划问题，该方法能很好地体现供配电网络中故障器件与断路器之间的关系，但该算法的动态模拟模型难以建立，且模型的鲁棒性会随着误差的增大而降低。

本文以智能建筑供配电系统为研究背景，提出一种基于贝叶斯网络与小波变换的故障诊断方法。当供配电网发生故障时，对电网的幅值、相位角和能量进行小波变换，并对故障特征量进行有效、高效提取。采用各种权重的熵值和简单的贝叶斯推理相结合的方法，得到各部件的故障度。采用量化相位融合方法作为贝叶斯的特征信息。对智能建筑供配电系统进行学习和培训，可用于完成智能建筑供配电系统的故障诊断。

1 智能建筑供配电系统的拓扑描述

4 母线、4 线路的供配电电网拓扑结构如图1 所示。其中，A、B、C、D 表示母线；L1—L4 表示线路；CB1—CB8 表示断路器；m 表示主保护；p 表示近后备保护；s 表示远后备保护；f 表示失灵保护。

对1 个具有m 条母线、n 条线路的供配电系统，可用m×n 阶关联矩阵S 表示其拓扑结构，S 中的非零元直观反映线路与母线之间的连接关系。将关联矩阵S 中的非零元置换为连接母线和线路的断路器，再将断路器状态分别置换为对应保护装置，可以先后实现对系统断路器和保护装置的拓扑描述。为有效表征系统中各元件的端口特性，将关联矩阵S 中的非零元分别按行置换为对应母线，或按列置换为对应线路，得到母线和线路拓扑矩阵。系统的关联矩阵可通过潮流计算数据获得。

关联矩阵S：

线路拓扑矩阵L：

母线拓扑矩阵M：

断路器拓扑矩阵CB：

母线保护拓扑矩阵Mm：

线路主保护拓扑矩阵Lm：

近后备拓扑矩阵Lp：

近后备拓扑矩阵Ls：

失灵保护拓扑矩阵CBf：

2 故障诊断流程

2.1 智能建筑供配电系统故障特征提取

当智能建筑供配电系统发生故障时，通常有三种故障度，分别为相角故障度、电压电流故障度和能量大小故障度。利用小波变换法对信号的分解与重构，借助熵值法得到权重，进而得到结果。假设智能建筑供配电系统中某一次故障有n 个元件。

（1）相角故障度。在发生故障前，将n 个元件各个相角进行小波变换后，得到系数矩阵，并进行奇异分解，得对角矩阵Λna：

在发生故障后，将n 个元件各个相角进行小波变换后，得到系数矩阵，并进行奇异分解，得对角矩阵Λnb：

则其相角故障度Sn可表示为：

（2）电压电流故障度。在发生故障前，将n 个元件电压和电流幅值进行小波变换后，取系数最大值Fna；在发生故障后，将n 个元件电压和电流幅值进行小波变换后，取系数最大值Fnb；则在故障发生前后电流和电压的幅值变化量为：

其电压和电流故障度xn可表示为：

（3）能量大小故障度。在发生故障前，将n 个元件的能量进行m 个分辨率小波变换，得到系数{Dna(k)}，n=1，2，…，k=1，2，…，则小波变换m 次后，能量ena为：

当发生故障后，将n 个元件的能量进行m 个分辨率小波变换，得到系数{Dnb(k)}，n=1，2…，k=1，2，…，则小波变换m 次后，能量enb为：

则强弱大小故障度为：

将上述三种故障度归一化处理，得到加权电气故障度特征：

智能建筑供配电网络中的电气元件的开关量的故障度T =[T1,T2,K,Tn]，则：

将加权后的三个故障特征Ci与电气元件的开关量的故障度T 进行融合，得到新的特征性故障度：

熵法通过计算“熵”来确定权重，即根据各特征的差异程度确定各指标的权重。当待确定对象的特征向量的值相差很大时，熵值很小，表明向量值所提供的信息量很大，其权重也大；反之，其权重也小。在对电流和电压故障度Xn提取之后，相角量Sn和从配电线路收集到的能量En进行相应的小波分解和重构，权重确定的方法为：

步骤1 标准化处理数据。

式中，Xij为i 电分量的j 特征向量的值；min{Xj}、max{Xj}为所有电气元件j特征向量的最小值和最大值。

步骤2 计算第i 个分量的第j 特征向量值的比例。

步骤3 计算指数信息熵。

式中，k=1/lna，其中a 为电气元件的数量。

步骤4 信息熵冗余度的计算。

步骤5 计算指标权重。

式中，h 为特征向量的数量，h=3。

2.2 基于小波变换和贝叶斯网络的供配电故障诊断步骤

故障诊断流程如图2 所示。采用小波变换的方法对单相短路、两相短路、三相短路、两相接地短路四类常见的故障及正常状态的数据进行预处理，建模分析，得到故障诊断结果。

迭代修正公式为：

式中，p(k)为联合概率；θ(k)为贝叶斯网络的参数；G(k)为网络结构；πi为配置索引因子。

3 算例分析

为验证本文提出方法的有效性，以IEEE-39 多节点复杂故障系统为研究对象，IEEE-39 系统网络拓扑如图3 所示。

系统包含39 条母线、46 条线路、92 个断路器。线路、断路器及保护均根据母线编号进行编排，如连接母线B03和B18的线路编号为L0318，相应B03侧的断路器记为CB0318，对侧记为CB1803。具体步骤如下：

步骤1 根据智能建筑物监测中心获得的电压电流幅值、相位角、能量强度等相关的基本电量，进行数据预处理工作。

步骤2 将小波变换按幅值、相位角和能量强度进行分解和重构后，根据不同的权重组合电气故障特征，采用贝叶斯推荐方法计算相应的元件开关故障特征，IEEE-39 系统先验概率的参数如表1 所示。从表1 可以看出，利用先验计算概率可对各故障度进行提取。根据继电保护系统的整定原则，保护和断路器告警的置信度及动作延时设置如表2所示。

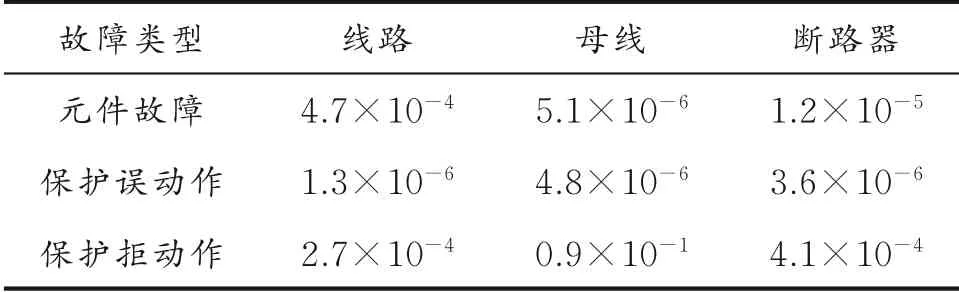
表1 IEEE-39 系统先验概率的参数

步骤3 将步骤2 得到的电气故障特征量和元件开关故障特征与简单的信息融合计算相结合，得到综合故障特征信息。

步骤4 构造贝叶斯网络，学习和训练步骤3 中获得的综合故障特征信息。取60 组训练数据，正常数据10 组，单相断路、单相接地短路、两相相间短路、两相接地短路、三相短路故障类型数据各10 组。对于故障元件的判定，选取30 组不同类别的数据进行实验，迭代次数为30，根据式(27)进行迭代。

步骤5 对于给定的故障特征，利用步骤3 获得的综合故障特征信息进行贝叶斯推理预测，并通过最大后验概率值的检验和估计来实现故障诊断。

表2 保护和断路器告警的置信度及动作延时设置

将本文的方法分别以单一的电气故障特征量作为贝叶斯的特征输入，单一元件故障开关量作为输入进行对比。算例测试结果如表3 所示。案例1-7的故障场景参考文献[13]，案例1-3 为告警信息完备情况的故障场景，案例4-7 为存在时标错误、信息漏报、误报等情况时的故障场景。从诊断结果可以看出，所提方法诊断故障元件与文献[13]的结果相同，但对于真实故障元件置信概率更高，非故障元件置信概率更低，同时能够推理得到元件的故障时间点约束区间，一定程度上提高了模型对故障元件的辨识能力。案例8 为本文算法对系统复杂故障的测试算例，该场景涵盖系统复杂多重元件故障，且伴随保护或断路器的拒动、误动及漏报等情况。本文算法与现有几种方法的故障诊断结果如表4 所示。

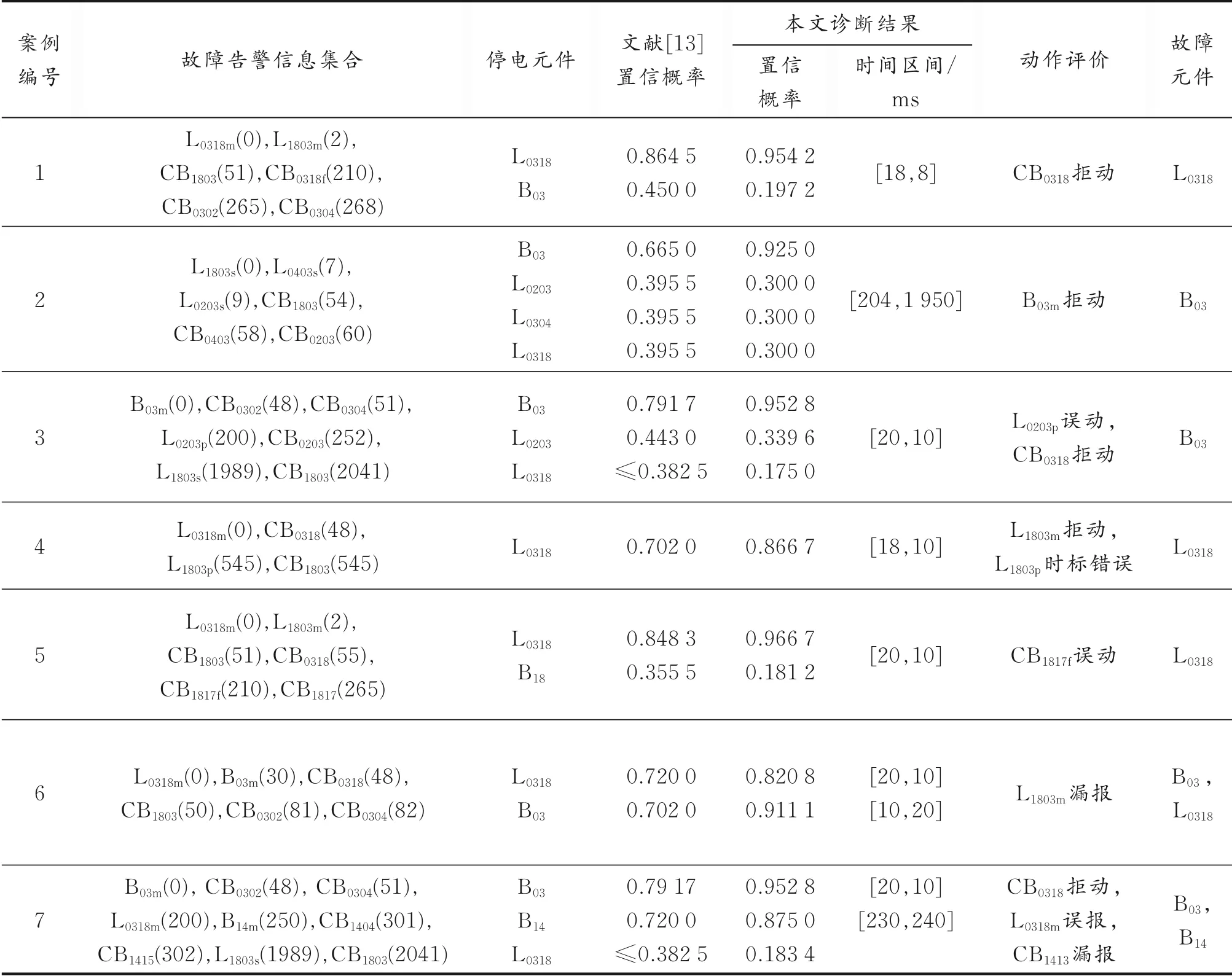
表3 IEEE-39 节点系统算例测试结果

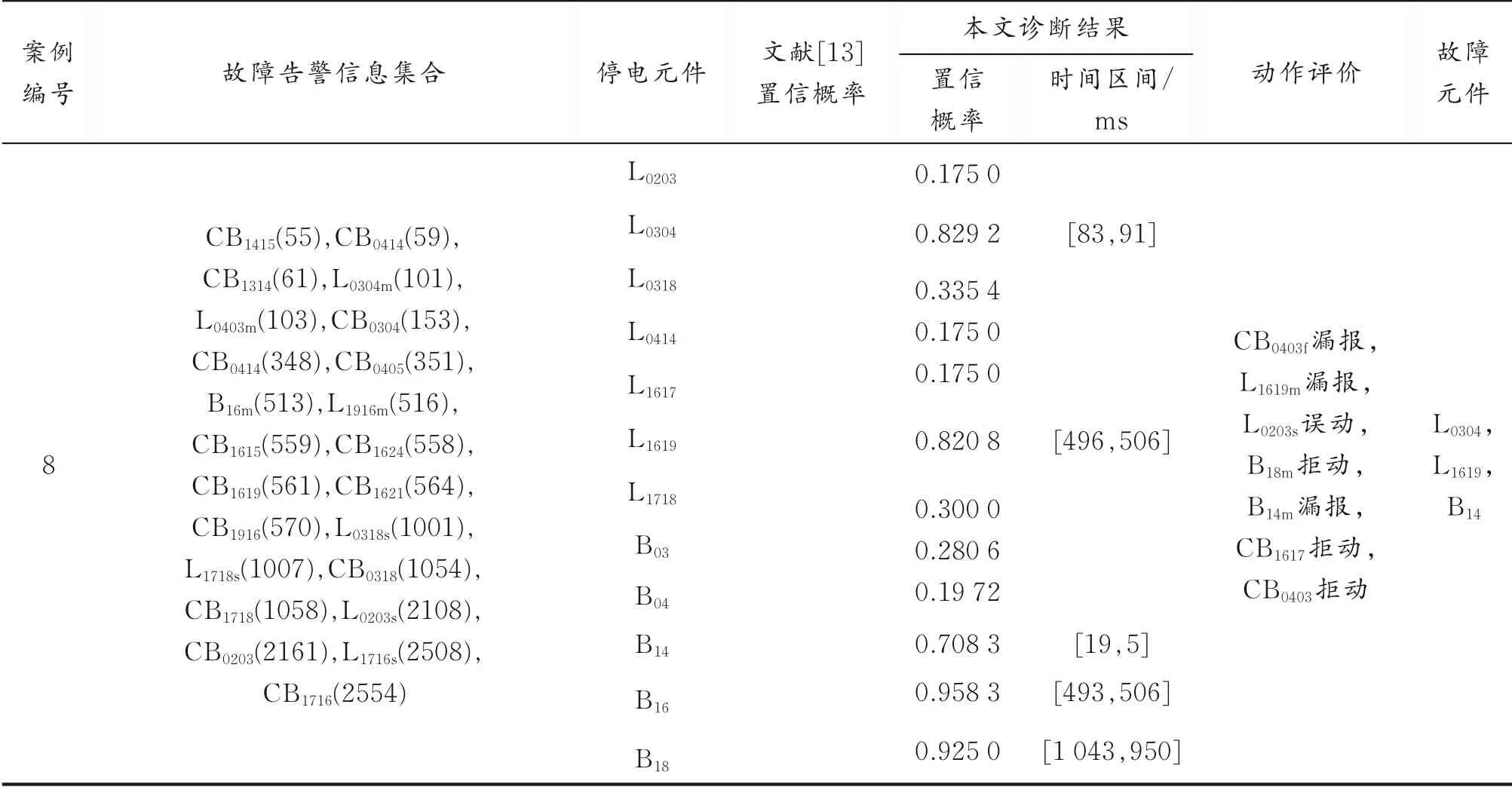
续表3

表4 本文算法与现有几种方法的故障诊断结果

仿真结果表明，所提方法对于简单故障以及复杂多重故障情况都能够正确判别故障元件，且在保护及断路器存在拒动、误动、漏报、误报以及时标错误等情况下均能有效判别故障元件，同时能够推理得到元件故障的时间点约束区间，具有较高的容错性。诊断时间均不超过1 s，且与故障复杂程度无关。如预先进行结线分析缩小故障诊断范围，诊断速度将进一步提升。此外，保护配置方案发生改变时，仅需调整贝叶斯网络和小波变换模型的推理路径。假如目标电网未配置失灵保护或失灵保护暂时退出运行，仅需删除贝叶斯网络和小波变换模型中的失灵保护推理路径即可，拓扑映射转换规则以及矩阵推理流程完全不变。

4 结 论

结合智能建筑供配电系统的特点，对其电网络拓扑结构和故障特征从理论上进行详细的故障特征分析，确定其故障类型。提出了一种基于小波变换和贝叶斯网络的智能建筑供配电网络故障诊断方法。与同类型方法相比，具有如下优势：（1）具有较强的适应性，并可以有效解决故障诊断的模糊性问题。（2）节省储存空间，大大降低计算的复杂程度，电网模型越大越具有优势。（3）具有较强的抗干扰和容错能力，当外界因素干扰时，诊断结果不受影响。（4）诊断精度高，速度快。最后，以IEEE-39 系统为研究对象进行仿真，结果表明，故障识别度高。