基于FEMSPH算法的柔性直升机着水数值模拟
(航空工业直升机设计研究所,江西景德镇 333001)
0 引言
由于直升机的应急救生设备决定了在发生事故进行水上迫降时,人员能否安全逃生,近年来越来越受到重视[1]。目前国内对直升机水上迫降的研究[2-3]还处于以模型试验为主,仿真分析辅助的阶段,而国外早已采取仿真分析取代试验的手段。直升机着水是一个复杂的流固耦合问题,其本质是结构物入水后所受到的冲击与滑水。目前很难模拟出柔性直升机以及应急浮筒的运动历程。本文旨在提供一种柔性直升机着水数值模拟方法,为早日实现仿真分析取代试验提供一种思路。
1 计算方法
本文采用有限元分析(FEM)以及光滑粒子流体动力学(SPH)耦合的方法来模拟直升机着水的整个过程。
光滑粒子动力学(SPH)的原理[4]是用一系列任意分布的粒子来表示问题域,粒子的速度、密度和位置受连续性方程、动量守恒方程以及能量守恒方程控制。用积分表达式对场函数进行近似,然后采用域内的相邻粒子对应的值叠加求和取代场函数的积分表达式,然后将粒子近似法应用于所有偏微分方程组的常函数相关项中,将偏微分方程组进行离散得到粒子的场变量。SPH方法是一种具有无网格、自适应属性的纯拉格朗日流体动力学求解方法。
有限元分析(FEM)的原理是将一个连续体求解域离散成若干个单元并通过它们边界上的节点相互连接,对每一个单元假定一个合适的近似解从而推导出求解域的近似解。针对传统的有限元方法不能模拟大变形问题的缺陷,采用有限元分析(FEM)以及光滑粒子流体动力学(SPH)耦合的方法[5]可以避免自由面大变形所造成的网格畸变问题,并且能准确地模拟出自由液面的变化以及水花的飞溅。
2 计算模型的建立
2.1 网格模型
首先对机身及浮筒组件进行网格绘制,确保所绘制的有限元网格没有多余的边界且网格的法向方向的一致。如图1所示为某型机的机身及浮筒组件模型,机身与浮筒之间通过绑带连接,机身及浮筒组件的最小网格尺寸很大程度上决定了整个仿真的速度,本文选用的机身及浮筒组件的最小网格尺寸为0.05m。

图1 机身及浮筒组件模型
选取长35m,宽30m,深5m的水体进行网格绘制,原则上水体网格尺寸应略大于机体及浮筒组件网格尺寸,本文选用的水体网格最小尺寸为0.0625m,将绘制完成的网格转换成SPH粒子,如图2。

图2 水体SPH粒子
2.2 材料模型
由于机身在着水过程中形变较小,为了减小计算量,将机体定义为不易变形的刚体材料。而浮筒以及绑带在着水过程中形变较大,为准确模拟其形变,将它们定义为膜单元进行建模。膜单元的特性为只能受压,不能受拉,与浮筒以及绑带的特性相吻合。水体在直升机冲击作用下发生剧烈的变形、移动,故水体采用SPH粒子建模,其中,粒子的粘性和光滑半径将关系到能否准确的模拟出水体的状态。
2.3 计算条件的定义
计算条件的定义主要在于接触模型的定义。接触模型的建立,使得多个拓扑不“相连”的结构可以传递载荷。直升机着水涉及多个接触关系,包括水体与机身、浮筒与机身、浮筒绑带与机身及浮筒、浮筒自接触等。以浮筒与机身的接触为例,它是用来计算机身和浮筒的运动关系和传力关系。在着水过程中浮筒受水体冲击,会向机身靠近,并挤压机身。建立机身和浮筒的接触,可以不断检测计算浮筒和机身的几何空间关系,并通过接近程度计算接触力,接触力作为作用力和反作用力施加给接触对双方的节点。接触厚度的大小设定和模型之间的初始距离关系需要严密控制,即需要使接触厚度小于接触双方模型的初始距离,否则会产生初始穿透,在整个时间历程中可能存在的接触关系均需要考虑。
其次是载荷条件的设置,将水体粒子、机身及浮筒组件赋予相应的初始速度、重力加速度等,然后再进行求解器设置,设定时间、控制迭代步长等,最后根据实际需求输出机身及浮筒组件重心处的加速度,获得直升机着水后的动态响应,确定最佳入水姿态角;输出浮筒载荷、浮筒对机体表面的压力等参数用于部件结构设计及强度校核。
3 计算结果分析
计算模型建立后,选取6°俯仰角,15.43m/s水平速度,1.5m/s垂向速度这一工况进行数值模拟。图3为这一工况下直升机的横向及垂向过载随时间的变化。图4为这一工况下直升机的横向及垂向速度随时间的变化。

图3 直升机的横向及垂向过载随时间的变化
如图3、图4所示,直升机在触水初期垂向过载加速度仍接近重力加速度,这主要是因为浮筒与机体之间的连接是通过绑带的柔性连接,后浮筒触水后,后浮筒向上运动,机体仍保持自由落体运动,浮筒与机体之间的相对位置发生了变化。在0.06s时,机体底部开始触水,机体受到了水体的垂向冲击力,垂向过载逐渐增加,垂向速度仍在增加,增加幅度减小,当垂向过载大于1时,垂向速度开始逐渐减小。在0.17s时,垂向过载达到最大值3.56g,随后垂向过载逐渐减小,垂向速度逐渐趋于零。在0.37s时,垂向过载小于1,垂向速度开始增加,机体在逐渐震荡中趋于稳定。在整个着水历程中,直升机的横向过载先增大后减小,在0.17s时达到最大值0.44g,直升机的横向速度在不断减小,直至趋于稳定。
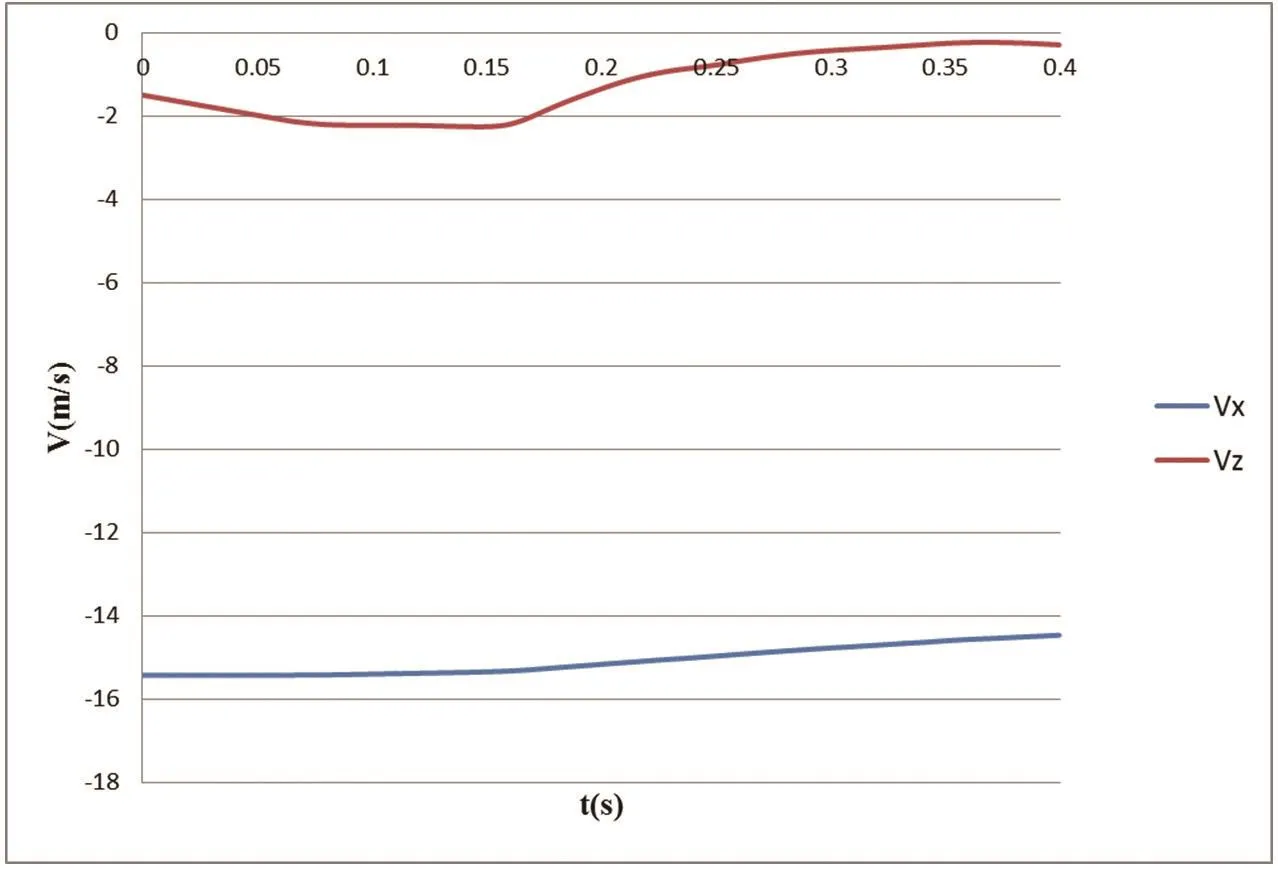
图4 直升机的横向及垂向速度随时间的变化
4 结论
(1)直升机柔性浮筒着水数值模拟直升机入水过程中的速度、过载峰值变化趋势与理论分析保持一致。
(2)直升机以某一垂向速度着水时,实际触水时垂向速度大于该垂向速度。
(3)直升机以6°俯仰角,15.43m/s水平速度,1.5m/s垂向速度在静水中着水时垂向过载最大达到3.56g。

