基于分段悬链线理论下带稳定索风缆找形分析

刘均华

(重庆交通大学 土木工程学院，重庆 400074)

0 前 言

稳定索是一种频率干扰索，连接主缆与风缆，主要作用是干扰主缆与风缆的共振频率[1]。目前，对于带稳定索的抗风缆研究较少，缺少相关研究理论。赵小潘[2]在研究大跨度管道悬索跨越结构受力行为时，表示相同截面面积及材料的稳定索与风拉索在不同工况下内力差值区别比较大，比值较大时，稳定索内力约为风拉索的1/2，同样，比值较小时为1/18。在以往工程设计中，风缆设计计算方法较为简单且没有考虑稳定索对风缆线形的影响，虽然稳定索内力较小，但在施工时肯定对风缆线形有一定影响。而杨永清等[3]在研究抗风缆对管线悬索桥动力特性的影响分析时认为，施加稳定索后可显著提高结构的动力特性(自振频率)。本文基于研究稳定索对全桥静、动力特性的影响，提出计算稳定索风缆线形的方法。

1 分段悬链线理论的计算原理

1.1 基本假定

通过比较空间悬索桥主缆与抗风缆具有许多相似之处，故采用空间悬索桥的分段悬链线理论对抗风缆找形。

悬索桥计算的基本假定：①假定风缆不考虑抗弯刚度影响，视为理想柔性索；②忽略风缆受力前后截面面积的改变；③风缆各索段符合线弹性理论；④风缆在竖向上只受沿弧长均匀分布的自重荷载以及风拉索的竖向分力[3]。

1.2 计算理论

根据以上假定能得到平面沿索长方向均布荷载作用下索段的分析，如图1所示。

图1 缆索受力示意图

根据图1取一索段AB，每沿米索重为q，风缆的弹性模量为E，风缆的截面面积为A，索段两端点的水平距离为l，竖向距离为h，索段的无应力长度为S0，S为变形后的形状长度。取左端点为拉格朗日坐标系下的原点，索段变形前的无应力长度在拉格朗日坐标为s，在自重作用下索段变形后，索段上任意的一点P到坐标原点的无应力长度坐标为p[4]。根据上面条件，得索段的几何约束方程：

(1)

1)取索段A、B端满足的边界条件为：当s=0，得x=0，y=0，p=0；当s=S0，得x=l，y=h，p=S。

根据平衡条件可知：

(2)

V(s)=V-qs

(3)

2)再根据胡克定律得张力与应变关系：

从而可得：

(4)

又可得：

(5)

3)当s=S0时，求解坐标x(s)，y(s)以及张力T(s)：

由上式积分，可得：

同理可得：

(7)

根据上述公式，在已知左端点的内力H0及V0,可得无应力长度s,以及x(s)、y(s)坐标。

2 带稳定索的风缆线形求解

2.1 计算公式

根据风缆节点受力平衡分析，如图2所示。

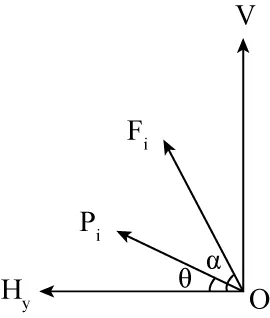
图2 风缆节点受力图

取风缆剖面图得平衡方程为：

Hxi=Hx,i-1

(8)

Hyi=Hy,i-1-Picosθ-Ficosα

(9)

Vi=Vi-1+Pisinθ+Fisinα-qS0i

(10)

(11)

式中， Hx为索段纵桥向水平分力；Hy为索段横桥向水平分力；V为索段竖向分力；S0为索段无应力长度；q为索段自重集度；Pi为i点上风拉索拉力；θ为风拉索与水平面夹角；α为稳定索与水平面的夹角；z、y为稳定索与主缆交点的横坐标与竖坐标；zi、yi为稳定索与风缆交点的横坐标与竖坐标；Fi稳定索的拉力。

对于抗风缆这种空间线形结构，两个相邻风拉索之间的节段只有自重，索段总是在一个铅锤面上，只是各索段的水平投影角度是变化的，只要将水平力分解到顺桥向和横桥向，通过这两个分力可以确定索段的空间走向[5]。

根据式(6)、(7)进一步推导得空间坐标与内力关系：

(12)

(13)

(14)

2.2 求解流程

2.2.1 无稳定索风缆求解流程

无求解流程见图3。

图3 风缆求解流程图

1)根据抛物线原理计算出风缆左端锚固点初始内力Hx0、Hy0和V0作为迭代初始值。

2)将初始内力带入风缆节点平衡方程中，求索段右端内力。

3)将求得的右端内力带入坐标与内力关系的方程中，求得该索段的无应力长度和右端的坐标位置。

4)考虑所取索段是否为最后一索段(右锚固端)。若不是，则需要重复(2)、3)步骤，直到是右锚固端索段时，进行下一步。

5)因为风缆是空间线形，并不知跨中垂点坐标值，故不能用其来判断线形是否收敛。在这里以总无应力长度作为控制参数，比较右锚固端设计坐标值与计算坐标值差值，是否满足迭代限值。若不满足限值需要通过影响矩阵法来修正初始内力，重新计算。若满足限值，则输出风缆坐标。

2.2.2 带稳定索风缆求解流程

在求解带稳定索的风缆线形时，发现每一根稳定索与水平面的夹角α是不相同的，本文利用主缆坐标与不考虑稳定索风缆坐标，在这里说明主缆没有考虑受到稳定索影响，初步计算稳定索初始夹角，如式(11)。

根据前面已求无稳定索风缆线形，进一步具体求解带稳定索的抗风缆流程见图4。

图4 带稳定索风缆求解流程图

1)先根据上述方法及条件，在不考虑稳定索内力的影响下，求不考虑稳定索的风缆坐标。

2)利用MIDAS建立主缆模型，初步得到主缆的坐标。

3)根据1)、2)求得的坐标计算每一根稳定索的初始夹角。

4)将初始内力带入风缆节点平衡方程中，求索段右端内力。

5)将求得的右端内力带入内力与坐标方程中，求无应力长度和坐标值。

6)考虑是否为最后一个索段，若不是就将这索段的右端内力作为下一索段的左端内力，带入3)或4)中；这里应该分情况考虑，一是索段带稳定索，就要先求稳定索夹角，再按以上步骤依次求解；二是如该索段无稳定索就直接带入风缆节点平衡方程，在这平衡方程中要去掉稳定索的部分，继续求解。

7)直到是最右端锚固端索段(最后一索段)，通过控制

的总无应力长度，比较右锚固端设计坐标值与计算坐标值差值，是否满足迭代限值，若不满足需要通过影响矩阵法来修正初始内力，并且将求到的风缆坐标作为新的迭代初始坐标与主缆坐标共同求解稳定索夹角，重复以上步骤，直到满足迭代限值。具体求解流程如图4所示。

3 结 语

抗风缆对于横向荷载作用在管道悬索桥的影响至关重要，要较精确地求出带稳定索抗风缆的无应力长度和坐标位置。本文根据空间悬索桥主缆线形求解方法，阐述了一般风缆线形求解的方法，同时分析了稳定索对风缆线形的影响，通过分段悬链线计算理论得出了带稳定索的风缆线形迭代计算方法，并给出求解带稳定索风缆的具体流程。

[ID:010590]