纳米改性变压器油物性的分子动力学研究
朱春晓 钱进 韦佳钰 杨生

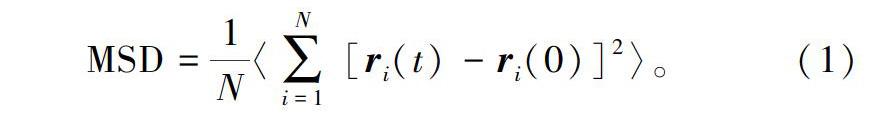
摘 要:为研究纳米改性后的变压器油的散热性能与绝缘性能的相容性关系,采用分子动力学方法对添加SiO2、ZnO纳米颗粒改性后的变压器油电导率、热导率开展数值模拟实验。结果显示:添加SiO2、ZnO纳米颗粒改性后的变压器油电导率、热导率较改性前均有所提高;改性后的变压器油电导率、热导率与模拟温度、体积分数呈非线性正相关;低体积分数时,纳米颗粒固有热导率与改性变压器油热导率不存在强关联关系;进一步研究各纳米颗粒体积分数下改性油品的散热性能和绝缘性能的相容性。在本研究范围内存在推荐值,体积分数为1%的SiO2改性变压器油,其热导率与电导率相容性最佳。
关键词:分子动力学;改性变压器油;电导率;热导率;相容性分析
中图分类号:TM214
文献标识码: A
变压器油不仅作为电气设备间的绝缘介质,同时也是散热流体,进一步提高变压器油的散热特性和绝缘特性,一直是领域内关注的热点课题[1-5]。国内外针对电气类油品的改性研究主要聚焦于单项物性参数的提升,CHOI C等[6]采用Al2O3、AlN改性变压器油的传热特性,结果显示在球形Al2O3颗粒体积分数为4%时,其传热能力可提高20%,而当AlN纳米颗粒体积分数为0.5%时,其传热能力提高了8%。缪金等[7]对ZnO纳米改性变压器油的相对介电常数进行了研究,结果表明当其体积分数较小时,改性后的相对介电常数略有增大,与ZnO纳米颗粒体积分数呈非线性正相关。杜岳凡[8]分析了TiO2半导体改性变压器油的老化特性和改性油纸绝缘特性,结果显示改性油工频和雷电击穿电压较未改性时提高了20%,改性油局部放电阈值电压较未改性时提高了10%,随着油品的进一步劣化,其工频击穿电压较未改性时可提高到100%,局部放电阈值电压可提高到20%。
本研究采用分子动力学方法对SiO2、ZnO纳米改性后的变压器油热导率、电导率开展数值模拟实验,分析纳米颗粒体积分数和温度条件对变压器油热导率、电导率的影响,并在《运行中变压器油质量标准(GB/T 7595—2017)》[9]规定的电导率限值下分析其纳米改性后的散热和绝缘性能的相容性,研究纳米添加物体积分数的最佳取值范围,以期为实际应用进行先期理论和可行性探索。
1 模型与模拟方法
1.1 模型的构建
本文以变压器油为基液,选择性能稳定和绝缘性较好的ZnO颗粒、SiO2颗粒作为纳米改性添加物,并根据基液分子结構以及纳米颗粒的构造为原型构建纳米改性变压器油分子模型。
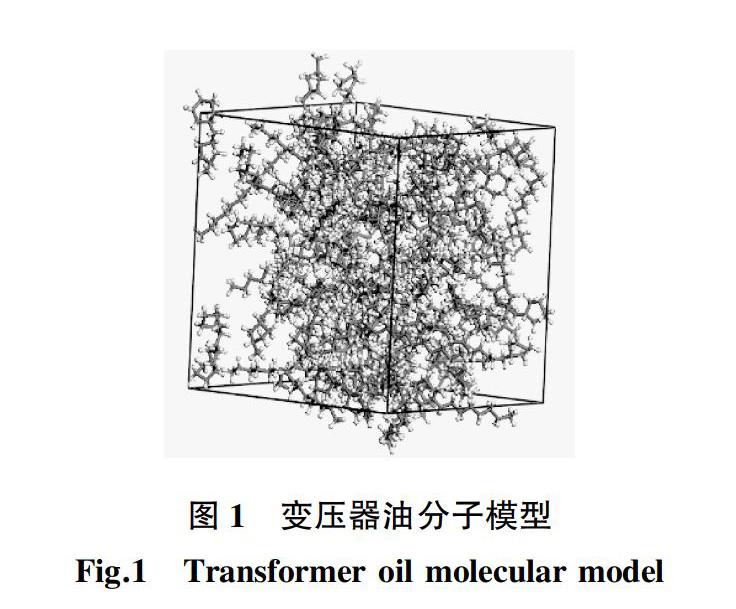
变压器油采用市售的克拉马依25#环烷基矿物油,刘枫林等[10]采用质谱仪对其成分进行了分析,该变压器油中环烷烃的质量分数为77%,链烃的质量分数为11.6%。本文采用无定形建模工具Material Studio,先分别构建各种环烷烃与链烃,然后根据各种烃类物质的比例来构建变压器油的模型,模型目标密度为0.9 g/cm3,为避免分子非等价地分布在晶胞中,采用5000步能量最小化方式优化晶胞,优化后模型中共含有3 596个原子,如图1所示。
ZnO晶体呈立方闪锌矿状,边长为4.63 ,密度为5 446 kg/m3;SiO2的初级原胞为立方结构,边长为7.16 ,密度为2 170 kg/m3。采用无定形建模方法构建ZnO分子模型和SiO2分子模型,再将其构建到基液分子模型中,调整纳米颗粒体积百分数分别为0.1%、0.3%、0.5%、0.7%和1%。ZnO、SiO2纳米改性变压器油分子模型见图2(a)、图2(b)。
1.2 模拟方法
本文研究的主要改性参数为电导率与热导率。首先,对于电导率的模拟计算,由于电导现象是通过离子扩散完成,因此计算不同组分的扩散系数,便可得到改性变压器油的电导率[11],从系统中粒子运动轨迹随时间变化的平均平方位移(mean square displacement, MSD),可得到研究体系的扩散系数[12]。MSD表示为:
式中:N是指扩散原子的数目,ri表示第i个粒子的位置矢量,对轨迹上所有的时间原点进行平均,则通过Einstein关系式由MSD可求得扩散系数:
式中:q为电子电荷,Di指扩散系数,kB为Boltzmann常数,T为模拟系统的开氏温度。
其次,采用平衡态分子动力学模拟方法计算热导率,该方法基于Green-Kubo线性响应理论,通过模拟系统的平衡状态计算出热导率[14],即:
式中:T为模拟系统的开氏温度,kB为Boltzmann常数,t为模拟时间,J为有效热流,V为模拟区域体积,rij为i原子与j原子之间的距离,ei为i原子的总能量,fij为i原子与j原子之间的相互作用力,vi为i原子的速度,uij为双体势能。
1.3 模拟过程
本文的模拟计算均在LAMMPS中进行,改性前油品的电导率为1.52 pS/m,热导率为0.105 6 W/(m·K),改性油应用对象为特高压变压器。
在电导率模拟过程中,选择在定容正则系综下,将模拟温度分别设定为298、308、318、328和338 K,采用Nosé-Hoover控温方法,选用Compass力场,采用LJ势函数计算范德华项,库仑函数计算静电作用,长程库仑力和范德华相互作用采用标准的Ewald方法计算,使用Verlet法进行数值积分[13],积分步长为1 fs,运行5 000步进行系统弛豫。当模拟体系达到平衡后,计算原子在晶胞中的均方位移和扩散系数,从而得到电导率。
在热导率模拟过程中,对于未改性变压器油模拟体系,其粒子数为3 596个,设定系统在目标模拟温度的正则系综下进行8 000步的温度矫正,将模拟体系的温度调整到目标温度直至系统达到平衡状态,随后转到微正则系综下执行100万步。
对于ZnO改性油的热导率模拟,ZnO的势函数需要计算其库伦力。设定锌原子和氧原子的电荷数分别为2.0、-2.0,采用Airebo势函数描述C、H间相互作用;再采用BKS势函数描述ZnO内部作用,其中ZnO内部库伦力采用Ewald方法计算,精确度为1.0×10-6;最后采用LJ势函数描述流体的连接,设置目标温度分别为298、308、318、328、338和348 K,纳米颗粒体积分数分别为0.1%、0.3%、0.5%、0.7%和1%,让系统在正则系综下运行8 000步,进行温度矫正,从而使模拟系统处于平衡状态,之后转为微正则系综执行100万步。
对于SiO2改性油的热导率模拟,通过混合势函数描述模拟体系中原子间相互作用力,用Airebo势函数描述C、H间相互作用;再采用BKS势函数描述SiO2内部作用,其中内部库伦力采用Ewald方法计算,精确度为1.0×10-6;最后采用LJ势函数描述流体的连接。硅原子和氧原子的电荷数分别为2.4、-1.2,其余流程与前述模拟过程相同。其中ZnO、SiO2短程作用力参数如表1所示。
2 结果与分析
2.1 不同温度对纳米改性变压器油电导率的影响
图3为ZnO改性油在各温度下其电导率与ZnO体积分数间的变化曲线。当ZnO体积分数一定时,随着模拟温度上升,ZnO改性油电导率将增大。在ZnO体积分数为0.1%时,改性油电导率随温度增大的幅度较小;当ZnO体积分数为0.7%时,改性油电导率增大的速度较快;当ZnO体积分数为1.0%时,随着模拟温度的升高,其电导率呈现继续抬升的趋势。
图4为SiO2改性油在各温度下其电导率与SiO2体积分数间的变化曲线。分析可知,相同体积分数下,SiO2改性油电导率随模拟温度上升而增大,但在SiO2体积分数为1.0%时,电导率增幅与温度升高的关联性在减弱。
2.2 纳米颗粒体积分数对改性变压器油电导率的影响
图5为采用ZnO改性油在各ZnO体积分数下其电导率与模拟温度间的变化曲线。分析可知,当温度一定时, ZnO改性油电导率与ZnO体积分数间呈非线性正相关。其中,在338 K、ZnO体积分数为1%时,改性后油品的电导率为2 042 pS/m,改性后的电导率比改性前增大了1 343倍,该值已远超变压器油运行电导率上限,不满足绝缘要求。
图6为SiO2改性油在各SiO2体积分数下其电导率与模拟温度间的变化曲线。分析可知,当温度一定时,SiO2改性油电导率与SiO2体积分数呈非线性正相关,且SiO2改性后油品的电导率与基液电导率仍然在同一数量级上,在338 K、SiO2体积分数为1%时,改性油电导率较未改性前仅增加了8倍。因此,采用SiO2对变压器油进行改性可使油品仍然具有较好的绝缘特性。
2.3 纳米颗粒体积分数对改性变压器油热导率的影响
对于电力系统中典型油浸式自冷变压器,选择变压器油正常工作温度25℃作为绝缘与导热性能相容分析的温度点,图7给出了温度为298 K时,改性后的油品热导率随ZnO、SiO2体积分数的变化曲线。分析可知,通过ZnO、SiO2改性后油品热导率得到了不同程度的提高。当纳米添加物体积分数为1%时,采用ZnO纳米改性后的油品热导率较改性前提高了14.5%,采用SiO2纳米改性后的油品热导率较改性前提高了10.3%。
值得注意的是,ZnO 纳米颗粒固有热导率为1.16 W/(m·K),SiO2为0.32 W/(m·K),在纳米颗粒体积分数为0.1%时,ZnO改性油热导率略小于SiO2改性油热导率,可见并非纳米颗粒固有熱导率越高,对变压器油热导率改性效果越好。
2.4 纳米改性变压器油散热和绝缘性能相容性分析
根据《运行中变压器油质量标准(GB/T 7595—2017)》,当变压器电压等级为500~1 000 kV时,电导率应小于100 pS/m。由前述内容可知,即使在ZnO体积分数为0.1%时,ZnO改性油电导率为129 pS/m,已经远大于变压器油运行质量标准,故不再考虑使用ZnO改性油品。以下讨论298 K时,SiO2改性油散热和绝缘性能相容性。
图8为298 K时SiO2改性油热导率、电导率随SiO2体积分数的变化曲线。分析可知,当SiO2体积分数为1%时,SiO2改性油热导率较改性前提高了10.3%,SiO2改性油电导率为8.93 pS/m,较改性前仅增加了8倍,仍满足运行标准。可见改性油热导率和电导率相容性依然良好,但若要继续增加其体积分数,由文献[15]可知,当SiO2体积分数达到1.5%时,其介质损耗与击穿电压将迅速增加,且稳定性较1%时大幅下降。故在本研究范围内,采用体积分数为1%的SiO2改性变压器油可满足绝缘性能的同时获得最佳的散热性能。
3 结论
通过分子动力学方法对改性变压器油的热导率、电导率进行了数值模拟计算,对其传热性能与绝缘性能的相容性进行研究,得出了以下结论:
1)ZnO纳米颗粒固有热导率为1.16 W/(m·K),SiO2纳米颗粒固有热导率为0.32 W/(m·K),当纳米添加物体积分数为0.1%时, ZnO改性油热导率却小于SiO2改性油热导率。可知低体积分数时,并非纳米颗粒固有热导率越高,对变压器油热导率改性效果越好。
2)ZnO改性油热导率虽然高于SiO2改性油热导率,但ZnO改性油电导率已超过变压器油运行时允许的电导率限值,因此ZnO不适用于该类变压器油改性。
3)在满足绝缘性能的条件下,采用纳米SiO2颗粒参与改性可显著地强化油品的散热性能,与未改性的油品相比,其热导率提高了10.3%。但受介质损耗、击穿电压及油品稳定性的制约,本研究范围内体积分数为1%的SiO2改性变压器油,其热导率与电导率相容性最佳。
参考文献:
[1]李加才, 陈继明, 朱明晓, 等. 基于反应分子动力学模拟的变压器油纸绝缘热解机制研究[J]. 绝缘材料, 2019, 52(6): 79-85.
[2]王磊, 牛铭康, 李超, 等. TiO2纳米变压器油击穿和电导特性的微观模型[J]. 高电压技术, 2019, 45(10): 3350-3356.
[3]王琪, 周远翔, 杨颖, 等. AlN纳米改性变压器油的电热性能及其应用研究[J]. 绝缘材料, 2017, 50(8): 106-112.
[4]李阳, 董明, 戴建卓, 等. 温度对纳米改性变压器油黏度影响的分子动力学模拟研究[J]. 绝缘材料, 2017, 50(7): 66-70.
[5]倪翔宇. 变压器油基磁性液体的制备及散热性能研究[D]. 合肥: 合肥工业大学, 2013.
[6]CHOI C, YOO H S, OH J M. Preparation and heat transfer properties of nanoparticle-in-transformer oil dispersions as advanced energy-efficient coolants[J]. Current Applied Physics, 2008, 8(6): 710-712.
[7]缪金, 董明, 任明, 等. ZnO纳米改性变压器油的相对介电常数模型[J]. 西安交通大学学报, 2013, 47(8): 121-126.
[8]杜岳凡. TiO2纳米粒子对变压器油绝缘和电荷输运特性的影响[D]. 北京: 华北电力大学, 2013.
[9]运行中变压器油质量: GB/T 7595—2017[S]. 北京: 中华人民共和国国家质量监督检验检疫总局; 中国国家标准化管理委员会, 2017.
[10]刘枫林, 徐魏. 石蜡基和环烷基变压器油的性能比较[J]. 变压器, 2004(7): 27-30.
[11]张国华, 薛庆国, 李丽芬, 等. CaO-Al2O3-SiO2熔體的电导率和离子扩散系数研究[J]. 北京科技大学学报, 2012, 34(11): 1250-1255.
[12]严六明, 严琪良, 刘洪来, 等. 模型溶液的分子动力学模拟及扩散系数计算[J]. 华东理工大学学报, 1997(4): 99-105.
[13]段晓惠, 李剑锋, 祝文军, 等. Li-KCl熔融界面上离子扩散的分子动力学研究[J]. 化学研究与应用, 2012, 24(4): 546-551.
[14]周敏. 掺杂硅中声子散射的分子动力学模拟[D]. 大连: 大连理工大学, 2009.
[15]周竹君, 金逸, 吴义华, 等. SiO2纳米改性变压器油特性研究[J]. 绝缘材料, 2016, 49(3): 47-52.
(责任编辑:曾 晶)

