一阶双曲最优控制问题的数值分析

张倩

摘  要：考虑了一阶双曲方程约束的最优分布控制问题，利用拉格朗日乘子方法给出一阶双曲最优控制问题的最优性条件，即状态方程、伴随方程和变分不等式。双曲方程中对流占主导，标准的有限体积元方法会产生物理震荡，该文采用高阶迎风有限体积元方法和变分离散相结合的方法对最优性条件进行数值离散。分别对最优性解的控制、状态和伴随给出了误差估计的结果。数值实验验证了方法的有效性和误差分析的结果。

关键词：双曲最优控制  有限体积元  最优性条件  变分离散

中图分类号：O241.1                          文献标志码：A                   文章编号：1672-3791（2020）11（b）-0254-03

Abstract： In this paper， the optimal distributed control problem with constraints for first-order hyperbolic equations is considered. By using the Lagrange multiplier method， the optimality conditions of the first-order hyperbolic optimal control problem are given， which consist of the state equation， the adjoint equation and the variational inequality. Convection is dominant in hyperbolic equation， and the standard finite volume element method will produce physical oscillation. In this paper， the high-order upwind finite volume element method and the variational discretization method are used to discretize the optimality conditions. The error estimates for the control， state and adjoint of the optimal solutions are given. Numerical experiments verify the effectiveness of the method and the results of error analysis.

Key Words： Hyperbolic optimal control; Finite volume element; Optimality conditions; Variational discretization

3  数值实验

在这个算例中，取I=[0，1]。为了验证方法的有效性和误差估计的结果，我们构造精确解。首先构造，通过伴随方程我们可以得到伴随的精确解为，再取最优的状态，那么由方程可确定函数f和yd。同时，我们取，ua=0.2和ub=0.8。

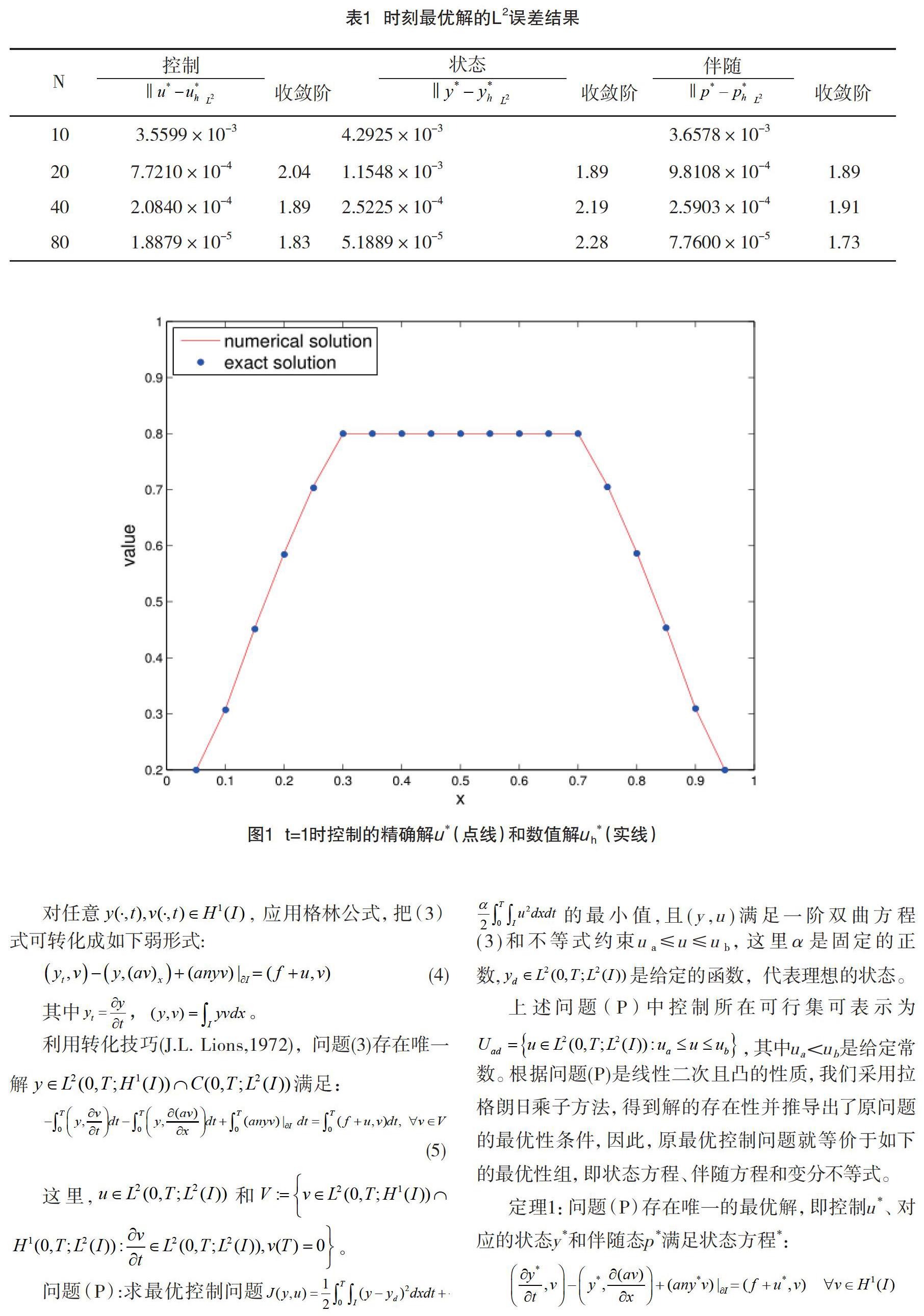
在表1中，我们分别列出了控制， 状态和伴随态的误差结果和相应的收敛阶。从表中可以看出在L2范数下误差的收敛阶为，这验证了定理3误差估计的结果。图1是t=1时刻控制的精确解u*和由高阶迎风有限体积元方法求得的数值解的图像。

参考文献

[1] W. Gong， M. Hinze， Z. Zhou. A priori error analysis for finite element approximation of parabolic optimal control problems with pointwise control[J]. SIAM Journal on Control and Optimization，2015，52（1）：97-119.

[2] S. Court， K. Kunisch， L. Pfeiffer. Optimal control problem for systems of conservation laws， with geometric parameter， and application to the Shallow-Water Equations[J].Interfaces & Free Boundaries，2018，21（3）：1-3.

[3] L. John， P. Swierczynski， B. Wohlmuth. Energy corrected FEM for optimal Dirichlet boundary control problems[J]. Numerische Mathematik， 2018（139）：913-938.

[4] R. Guo and T. Lin. An immersed finite element method for elliptic interface problems in three dimensions[J]. Journal of Computational Physics， 2020（414）：109478.

[5] Q. Zhang，J. Yan，Z. Zhang. High-order upwind finite volume element method for first-order hyperbolic optimal control problems[J].ANZIAM Journal， 2016，57（4）：482-498.

[6] Q. Zhang，K. Ito，Z. Li， et al. Immersed finite elements for optimal control problems of elliptic pdes with interfaces[J].JOURNAL OF Computational Physics，2015，298（C）：305–319.

[7] 張倩.几类PDE约束最优控制问题的数值方法研究[D].南京师范大学，2016.

[8] 郁鹏飞，傅勤.一阶双曲型偏微分多智能体系统的迭代学习控制[J].中国科技论文，2019，14（11）：1185-1191.