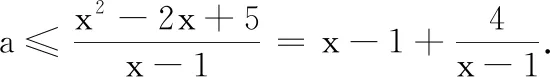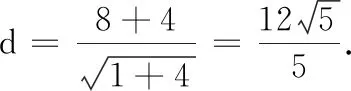高二数学测试
一、单项选择题(本大题共8小题,每小题5分,计40分)
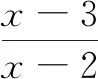
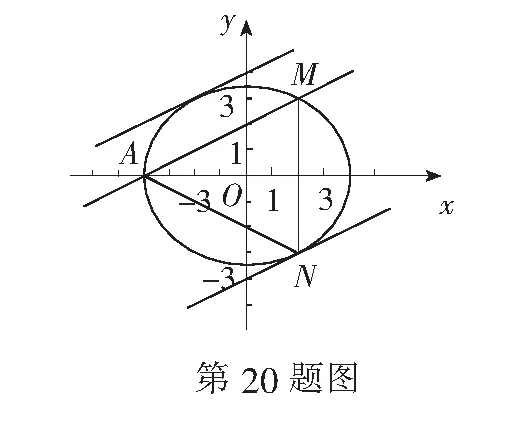
(A){x|2 (B){x|x>2} (C){x|x<3} (D){x|x<2或x>3} (A)10 (B)-10 (C)14 (D)-14 (A) 1 (B) 2 (C) 4 (D) 8 (A)11 (B)10 (C)9 (D)8 9. 等差数列{an}是递增数列,满足a7=3a5,前n项和为Sn,下列选择项正确的是( ) (A)d>0 (B)a1<0 (C)当n=5时Sn最小 (D)Sn>0时n的最小值为8 10. 嫦娥四号月球探测器于2018年12月8日搭载长征三号乙运载火箭在西昌卫星发射中心发射.12日下午4点43分左右,嫦娥四号顺利进入了以月球球心为一个焦点的椭圆形轨道,如图中轨道③ 所示,其近月点与月球表面距离为100公里,远月点与月球表面距离为400公里,已知月球的直径约为3 476公里,对该椭圆下述四个结论正确的是( ) (A)焦距长约为300公里 (B)长轴长约为3 988公里 (C)两焦点坐标约为(±150,0) 11. 若正实数a,b满足a+b=1,则下列说法正确的是( ) 12.已知点F是抛物线y2=2px(p>0)的焦点,AB,CD是经过点F的弦,且AB⊥CD,AB的斜率为k,且k>0,点C,A在x轴上方.则下列结论中一定成立的是( ) (B)四边形ACBD面积最小值为16p2 13.已知数列{an}的前n项和Sn=n2,则an=______. 14.已知2a+3b=4,则4a+8b的最小值为______. 15.已知F是抛物线C:y2=8x的焦点,M是C上一点,FM的延长线交y轴于点N.若M为FN的中点,则|FN|=______. 18. (本小题满分12分) 如图,四边形ABCD为正方形,PD⊥平面ABCD,PD=DC=2,点E,F分别为AD,PC的中点. (1)证明:DF∥平面PBE; (2)求三棱锥D-PBE的体积. 19. (本小题满分12分)已知函数f(x)=x2-(a+2)x+4(a∈R). 第三方支付是指具备一定实力和信誉保障的独立机构,通过互联网对接而促成双方进行交易的网络支付模式。第三方支付作为独立的中间平台,它的两端连接着消费者,商户和国内外的各大商业银行,可以提供较为安全,独立,有保障的交易服务。第三方支付已经不仅仅是一种简单的互联网支付,现在运用第三方支付进行线上线下交易已成为主流。两种模式,一种运营模式是完全独立于电子商务网站,仅为用户提供支付解决方案而不负担保功能;另一种以B2C、C2C电子商务网站并提供担保功能的第三方支付模式。 (1)解关于x的不等式f(x)≤4-2a; (2)若对任意的x∈[1,4],f(x)+a+1≥0恒成立,求实数a的取值范围. (1)求C的方程; (2)点N为椭圆上任意一点,求∆AMN的面积的最大值. 21.(本小题满分12分)Sn为等差数列{an}的前n项和,且a1=1,S7=28.记bn=[lgan],其中[x]表示不超过x的最大整数,如[0.9]=0,[lg 99]=1. (1)求b1,b11,b101; 参考答案 一、单项选择题 1.D;2.B;3.D;4.C; 5.A;6.B;7.A;8.C. 二、多项选择题 9.ABD;10. AD;11. AB;12.ACD. 三、填空题 13.2n-1;14.8;15.6;16.-2. 四、解答题 因为DF⊄平面PBE,EG⊂ 平面PBE,所以DF∥平面PBE. 19.(1)f(x)≤-2a+4,即x2-(a+2)x+2a≤0,得 (x-a)(x-2)≤0.当a<2时,不等式解集为{x|a≤x≤2};当a=2时,不等式解集为{x|x=2};当a>2时,不等式解集为{x|2≤x≤a}. (2)对任意x∈[1,4],f(x)+a+1≥0恒成立,即x2-(a+2)x+5+a≥0恒成立,即对任意x∈[1,4],a(x-1)≤x2-2x+5恒成立. 当x=1时,不等式为0≤4恒成立,此时a∈R. 综上,a≤4. (2)设与直线AM平行的直线方程为x-2y=m,如图所示,当直线与椭圆相切时,与AM距离比较远的直线与椭圆的切点为N,此时∆AMN的面积取得最大值. 令Δ=144m2-4×16(3m2-48)=0,可得m=±8.故与AM距离比较远的直线方程为x-2y=8,直线AM方程为x-2y=-4. 21.(1) 设{an}的公差为d,则7+21d=28,解得d=1.所以{an}的通项公式为an=n.b1=[lg 1]=0,b11=[lg 11]=1,b101=[lg 101]=2. 所以数列{bn}的前1 000项和为1×90+2×900+3×1=1 893.


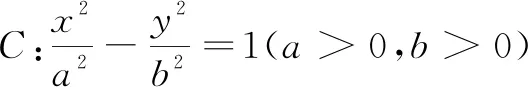

二、多项选择题(本大题共4小题,每小题5分,计20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分)


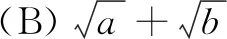




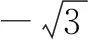
三、填空题(本大题共4小题,每小题5分,计20分)
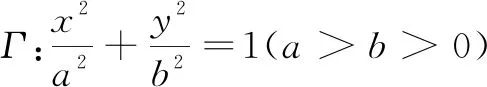
四、解答题(本大题共6小题,计70分. 解答应写出文字说明、证明过程或演算步骤)