面向车联网通信的非平稳信道仿真方法
华博宇,朱秋明,何小祥
(南京航空航天大学 电子信息工程学院,江苏 南京 211106)
0 引 言
车联网(Vehicle-to-X,V2X)是第五代(the fifth gene-ration,5G)移动通信重要应用之一,而构建精确车-车(Vehicle-to-Vehicle,V2V)信道模型及仿真技术,是有效设计和评估车载通信设备的重要理论基础[1]。近年来的车联网信道模型中,几何随机模型具有适中的精度和复杂度,是较为主流的模型[2-4]。例如,文献[5]假设车辆均速直线运动,提出基于射线跟踪的信道模型;文献[6]提出单环几何信道模型,分析车辆速度的角度变化。另一方面,准确快速的仿真方法是复现信道传播特性的关键技术,而面向车联网场景的仿真方法需要支持非平稳特性的模拟。例如,文献[7]通过泰勒级数展开的方法得到车辆时变的速度参数;文献[8]考虑速度的时变角度,实现任意移动轨迹的参数计算;文献[9]把非平稳信道转化为若干平稳子信道进行仿真,但存在输出相位的不连续[10];进一步地,文献[11]提出复谐波叠加的改进仿真方法,实现参数的连续渐变。
本文提出一种面向车联网通信场景的非平稳信道建模仿真方法,该方法选择积分形式的多普勒参数项,使得信道输出的衰落相位连续时变;在参数计算方面,该方法考虑速度和角度的时变特性,并联合多普勒频率参数进行建模,为车-车通信场景中快速时变参数的生成和演进提供一种高效的算法。此外,本文分析推导了信道统计特性的理论表达式用于评估仿真方法的性能,并通过数值仿真进行验证。
1 车-车非平稳信道模型
在车联网通信场景中,大部分信号的发射端和接收端都处于移动的车辆上,且车辆的移动速度通常随时间发生改变,导致多普勒频率的时变性,最终表现为整个信道的非平稳性。这种非平稳性在信道建模过程中,体现为特定参数的时变性。
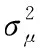
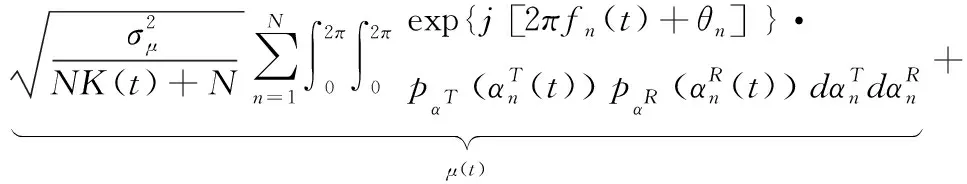
(1)
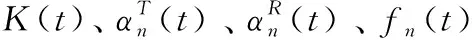
值得注意的是,文献[10]指出复谐波叠加方法生成的信道输出相位与多普勒频率不能准确对应,而积分项的引入可以改善这个问题。本文将此方法应用于存在视距分量的信道仿真模型中,并做出改进,为了与理论参数区分,用~符号表示仿真模型参数。
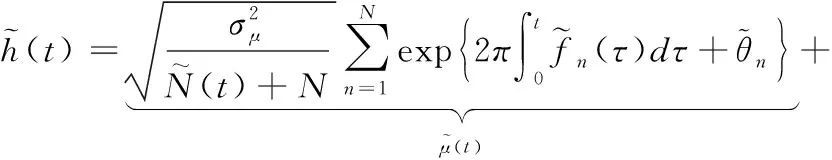
(2)
2 信道参数计算和统计特性分析
2.1 时变参数计算及演进
高效精确的参数计算方法能够保证仿真信道具有与参考模型一致的统计特性,也是仿真方法的关键步骤。文献[13]中的实测数据表明,即使在收发端运动的环境下,非平稳信道依然存在可近似为广义平稳的时域区间,因此非平稳信道的参数也可划分为多段进行近似计算。
为了对多普勒频率进行实时计算,将文献中对散射径的假设推广,在对仿真信道的第n条散射径建模时,无论实际信号经过几次散射,只考虑散射径首尾两个等效散射簇,并假设发射端与接收端之间的距离远大于收发端各自与等效散射簇之间的距离。此外,本文从多普勒频率的定义出发,将收发端运动速度的幅值与角度一并纳入参数计算方法中,使得多普勒频率为连续时变的随机过程。以下以直射径为例,给出时变多普勒频率的具体计算步骤。
首先,假设v为运动速度,λ为信号载波波长,α为入射波与运动方向夹角,则多普勒频率可表示为
(3)
车联网通信场景下,车辆之间的距离远大于信号载波波长,可认为收发端彼此独立,则直射径的时变多普勒频率可表示为由发射端及接收端各自移动造成的多普勒频移之和,即
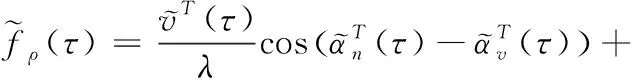
(4)
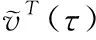
其次,进一步考虑收发端相关参数的时变特性,短时间间隔内收发端的时变离开角和到达角可近似表示为如下线性模型
(5)
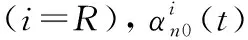
(6)
(7)
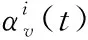
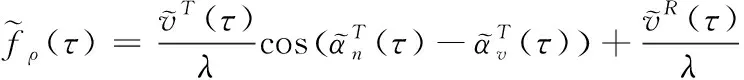
(8)
最后,引入积分形式使时变多普勒频率对应的相位连续,得到最终的多普勒频率参数可表示为
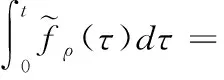
(9)
2.2 统计特性分析推导
考虑到信道单次输出的随机性,验证仿真方法输出信道的准确性通常选用比较信道统计特性的方法。实际中,用于描述信道特性的指标主要包括一阶统计特性PDF、二阶统计特性ACF和PSD。
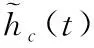
(10)
式中:k∈{c,s}用来标识同向分量和正交分量。进一步地,直射径和散射径可分别表示为
(11)
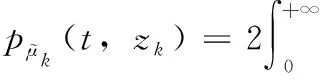
(12)
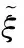
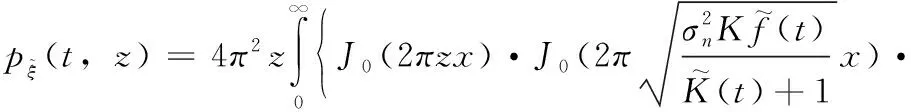
(13)
其次,仿真模型的同向及正交分量均包含直射径和散射径两部分,模型最终输出的信道随机衰落的ACF定义为
rhh(τ)=rmm(τ)+rμμ(τ)=
E{m*(t)m(t+τ)}+E{μ*(t)μ(t+τ)}
(14)
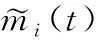
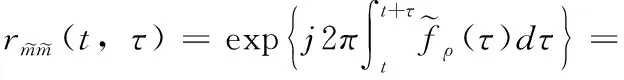
(15)
(16)
最后,根据维纳辛钦定理,信道随机衰落的PSD可表示为ACF的傅里叶变换,即
(17)
本文提出的仿真方法通过设置收发端的运动速度和运动角度,可生成任意移动轨迹的车联网通信场景下的信道随机衰落,并通过式(10)~式(17)得到信道的一阶统计特性PDF及二阶统计特性ACF和PSD的理论值。
3 数值仿真与讨论
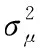
利用本文方法仿真输出的信道包络的时变三维PDF如图1所示,为便于比较理论值与仿真值,图2给出了二维切片PDF。鉴于信道包络的PDF与多普勒频率无关,仿真模型的PDF理论值可由式(13)得到。从图中可看出,在t=0 s,1 s和2 s时刻,对应莱斯因子K=0,3和6这3种情况下,本文提出的仿真方法生成的仿真值与理论值高度吻合,注意到当莱斯因子K=0时,视距分量为零,莱斯衰落退化为瑞利衰落。此外,仿真精度的高低与总支路数的多少呈正相关。
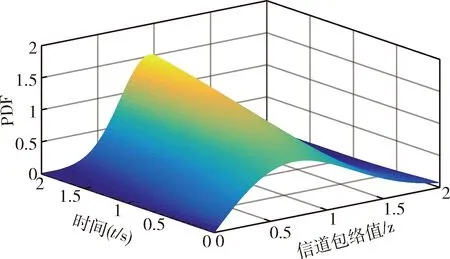
图1 时变PDF三维理论值
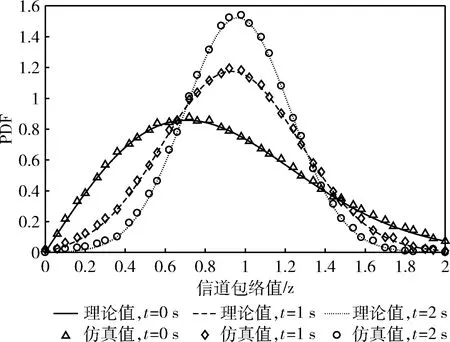
图2 时变PDF理论值与仿真值
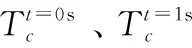
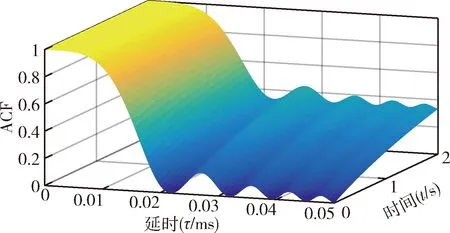
图3 时变ACF三维理论值
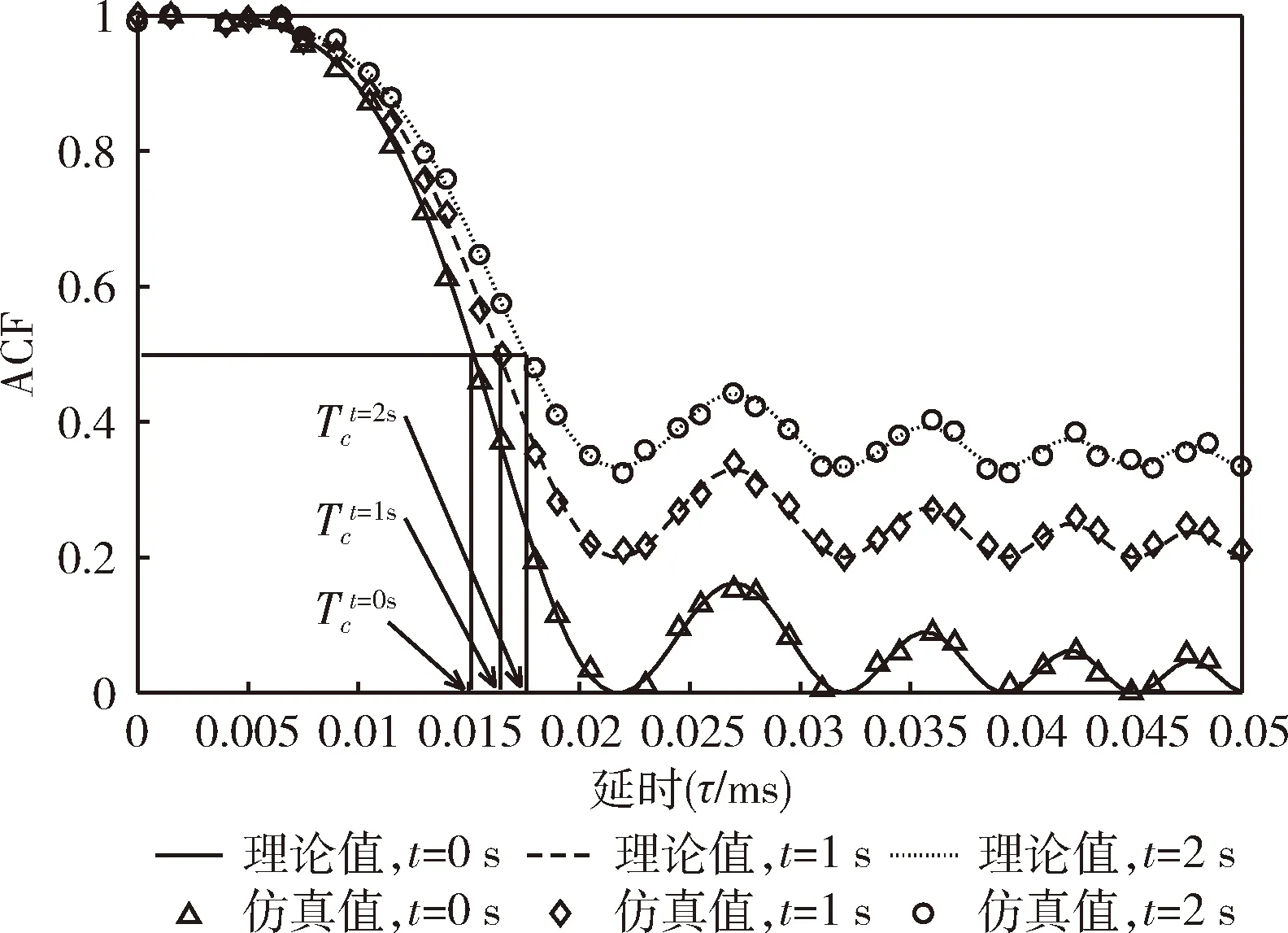
图4 时变ACF理论值与仿真值
图5给出了由式(17)得到的信道时变多普勒PSD的三维理论值,为比较理论值与仿真值,对应t=0 s,1 s和2 s时刻的二维切片PSD如图6所示。由于仿真支路的有限性,3个时刻的仿真值与模型理论值存在一些幅值上的偏差,但均具有相对一致的趋势。从图中可以看出,信道的PSD在整个仿真时间内随着时间平滑演变,良好复现了车联网场景下非平稳信道参数的时变特性。
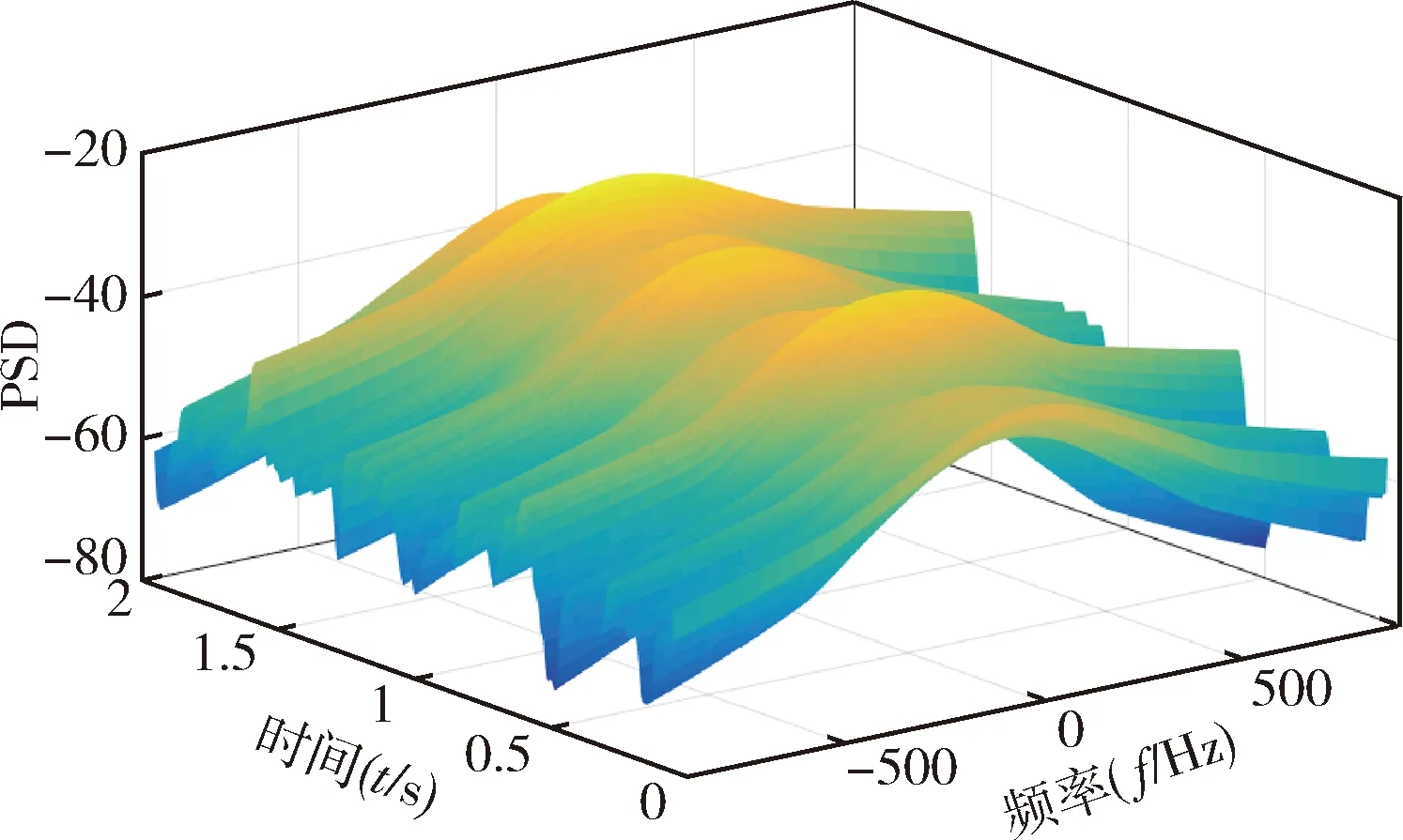
图5 时变PSD三维理论值
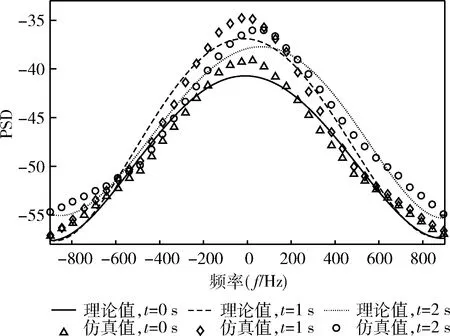
图6 时变PSD理论值与仿真值
4 结束语
本文针对收发端均处在移动状态的车联网通信场景,提出了一种车-车非平稳信道仿真方法,并从仿真模型、参数计算和统计特性3个方面对该方法进行了深入研究。通过积分项的引入,本文提出的仿真方法生成的信道更加符合实际场景;同时,基于定义改进的参数计算方法可以高效精确地获得信道的多普勒频率,为快速时变的车-车通信参数提供了一种高效的生成与演进算法。数值仿真结果表明,本文提出的仿真方法能够良好地再现车-车非平稳信道的时变特性,输出信道的统计特性如PDF、ACF和PSD均与理论值基本吻合,可用于未来车联网场景下的无线信道建模仿真和车载通信系统的性能评估等环节。

