一种超声椭圆切削装置的振子有限元分析

陈 霞

(仁宝电子科技有限公司，江苏 昆山 215300)

0 引言

超声振动加工技术诞生于20世纪50年代，主要用于解决脆硬性材料难加工问题。随着科学技术的发展，国内外学者对超声加工领域进行了进一步深入研究，使得超声加工这一技术向着超精密化方向发展。从一维振动切削到二维振动切削，研究人员取得了许多显著的成果。张德远、李勋等[1-2]在一维振子的模型上偏离轴线的位置增加了配重块，当换能器接通高频电信号后产生高频纵向振动，传递到刀具，由于配重相对轴线产生的不对称的弯矩作用，从而得到弯曲振动和纵向振动，在变幅杆的最前端复合形成了椭圆振动轨迹。李华、殷振等[3-4]在变幅杆上开特殊角度的斜槽，通过斜槽的模态转换作用，将换能器的纵向振动转变为一部分的弯曲振动，在刀尖处形成椭圆振动轨迹。

目前椭圆轨迹振动切削主要是通过上述两种方式在刀具的刀尖处实现[5-6]，本文旨在研究出一种异形变幅杆，实现刀尖处的椭圆轨迹振动切削。振子的工作原理是：通过单路电信号进行激励，压电陶瓷片将超声波能量转化为高频振动，经过变幅杆传导后放大，最终在异形变幅杆前端复合成为一个椭圆振动轨迹，刀尖沿着椭圆轨迹进行高频振动，与工件进行周期性接触分离。这种切削与普通切削相比较，可以降低刀具切削的温度和切削力，提高工件的表面质量。

1 振子变幅杆的设计

振子在切削装置中起着重要作用，是整个切削装置的核心所在，振子的结构示意图如图1所示。振子的部件主要包括后盖板、前盖板、压电陶瓷片、变幅杆等。

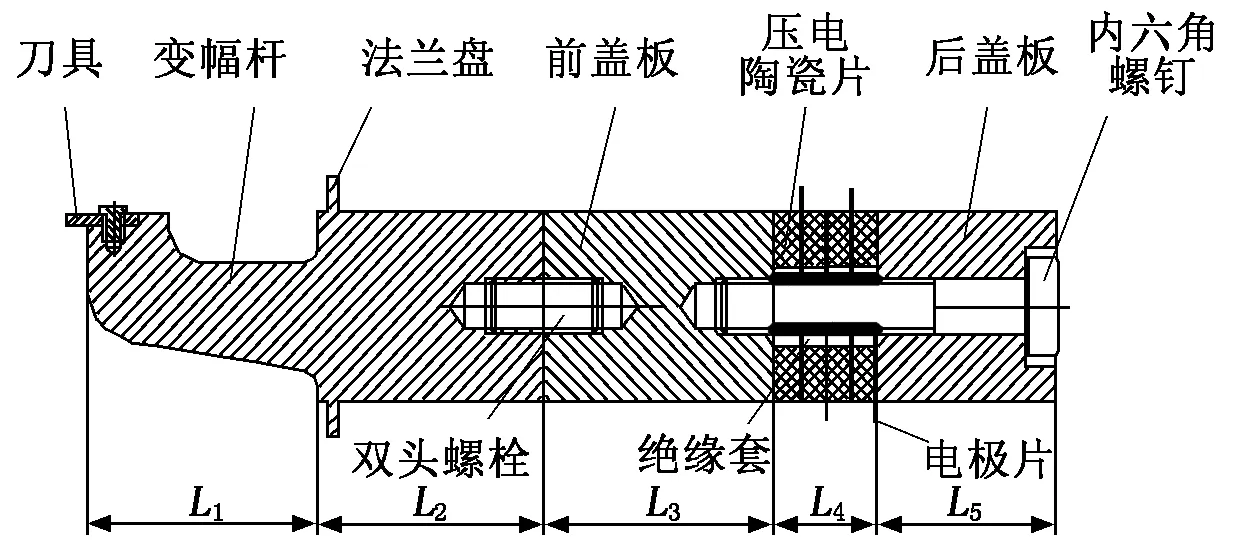
图1 振子结构示意图

变幅杆是振子设计最关键的部分，是能否在切削刃的前端形成椭圆运动轨迹的核心所在。变幅杆的材料可以为铝合金，也可以为316L不锈钢或者45钢。根据变幅杆的设计原理，通过公式计算得到振子各部分尺寸，如表1所示。

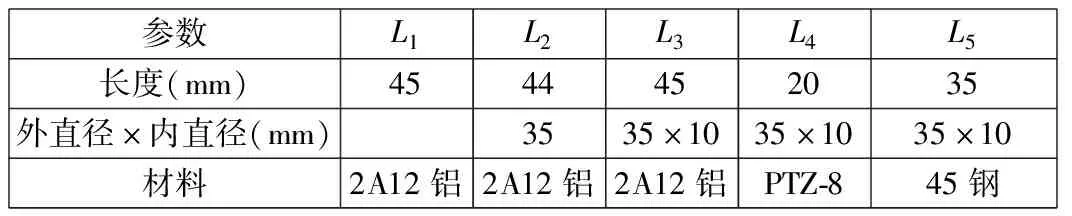
表1 振子的结构尺寸

2 振子的前处理

采用ANSYS软件对切削装置的振子进行建模，利用命令流进行模型的搭建，振子中的压电陶瓷采用的单元类型为Solid98，前盖板、后盖板以及变幅杆的单元类型为Solid95，采用自由网格划分得到的振子有限元模型如图2所示。

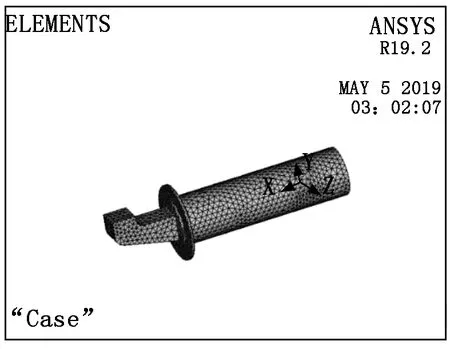
图2 振子的有限元模型

3 振子的后处理

3.1 振子的模态分析

通过模态分析可以确定切削装置振子的固有频率，由此可以判断换能器是否对电功率进行了高效的转换。设置正负电极的耦合面电压为0 V，模态求解的方法采用Block Lanczos，求解的范围为25 kHz～35 kHz，然后通过软件的界面操作可以获得振子的模态云图以及轴向振动幅值曲线图，如图3和图4所示。

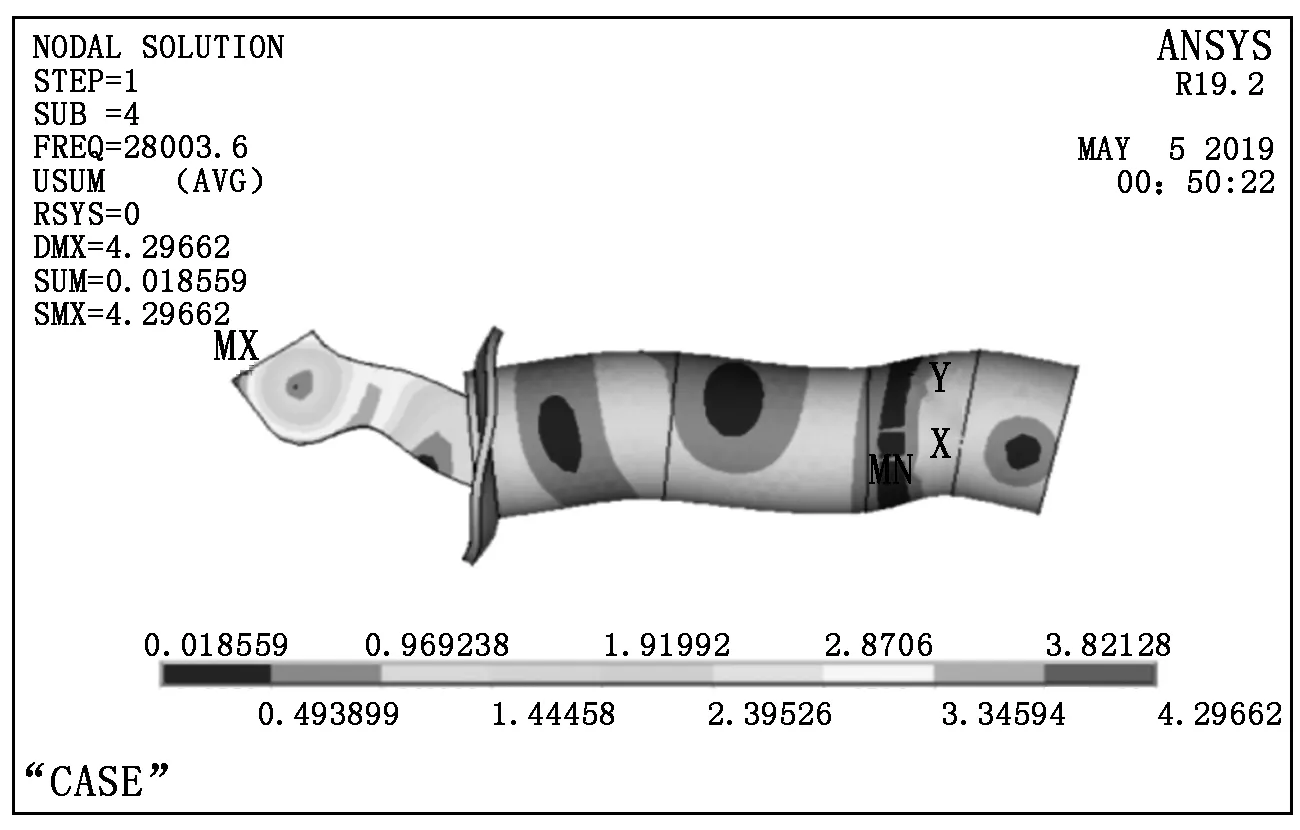
图3 振子的振动模态云图

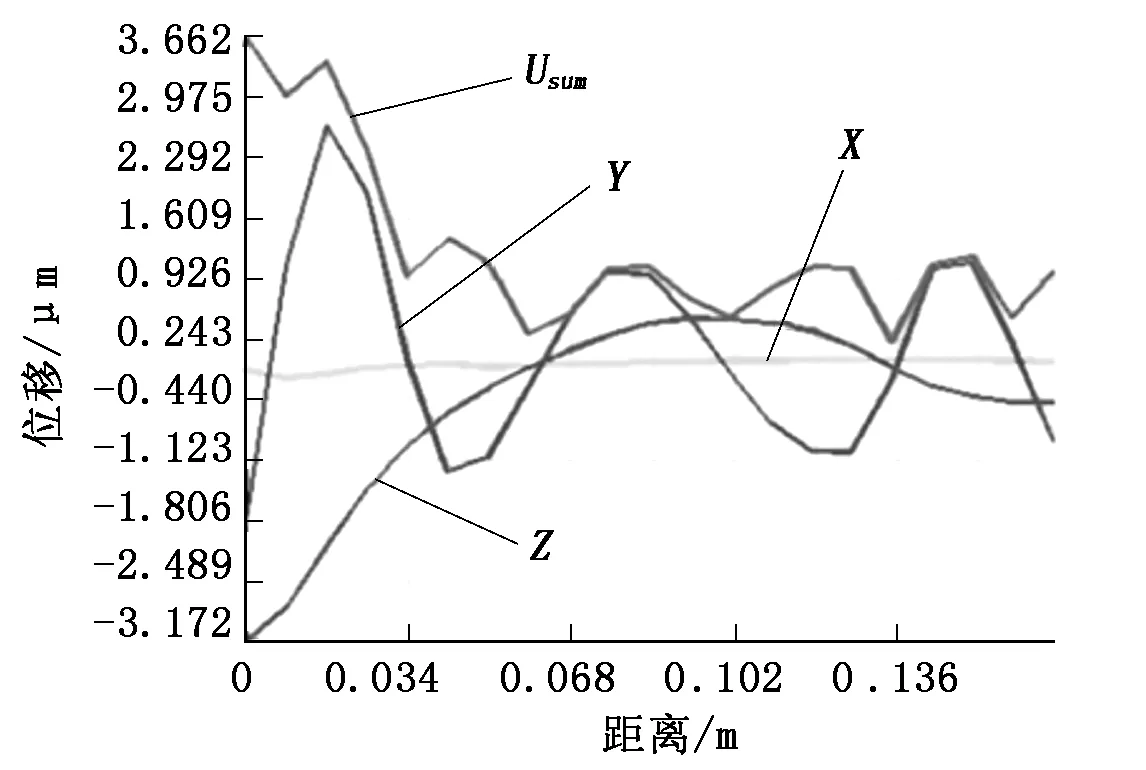
图4 振子轴向振动幅值曲线图

通过图3的振动模态云图可以观察出振子最左端为振子发生最大形变的位置；通过图4振子轴向振动幅值曲线可以观察到振子在X向、Y向、Z向位移以及振子总体振动偏移具体量Usum，该振子的谐振频率为28.003 kHz，前端有弯曲振动和纵向振动，在振子最左端输出的Z向振幅最大，在压电陶瓷片附近(0.136 m处)最小，与预期一致。

3.2 振子的瞬态分析

对振子进行瞬态分析，进而确定振子上的刀尖点在一瞬间的运动轨迹。在振子上设置28 kHz的频率，设置500 V的正弦电压，利用Full的完全算法，对所选取的载荷点进行瞬态分析，紧接着通过POST26后处理器提取选取点的运动轨迹，可以得到刀尖位置的时域曲线图以及刀尖运动轨迹图，分别如图5和图6所示。

从图5中可以发现，刀尖处在Y轴方向和Z轴方向上随着时间振动曲线均为正弦趋势，两个方向上的正弦运动合成了如图6所示的刀尖处的椭圆运动轨迹图。

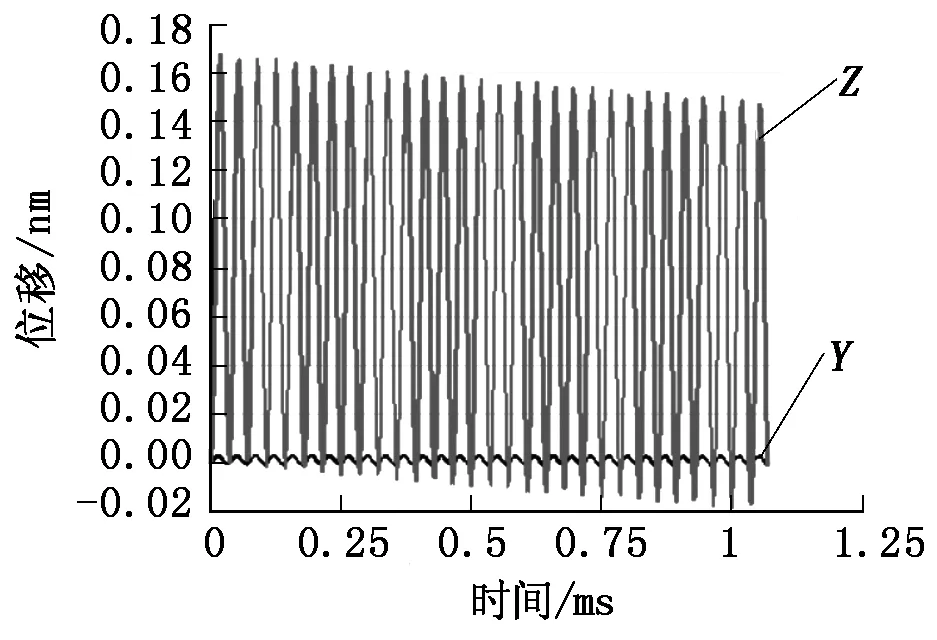
图5 刀尖时域曲线图

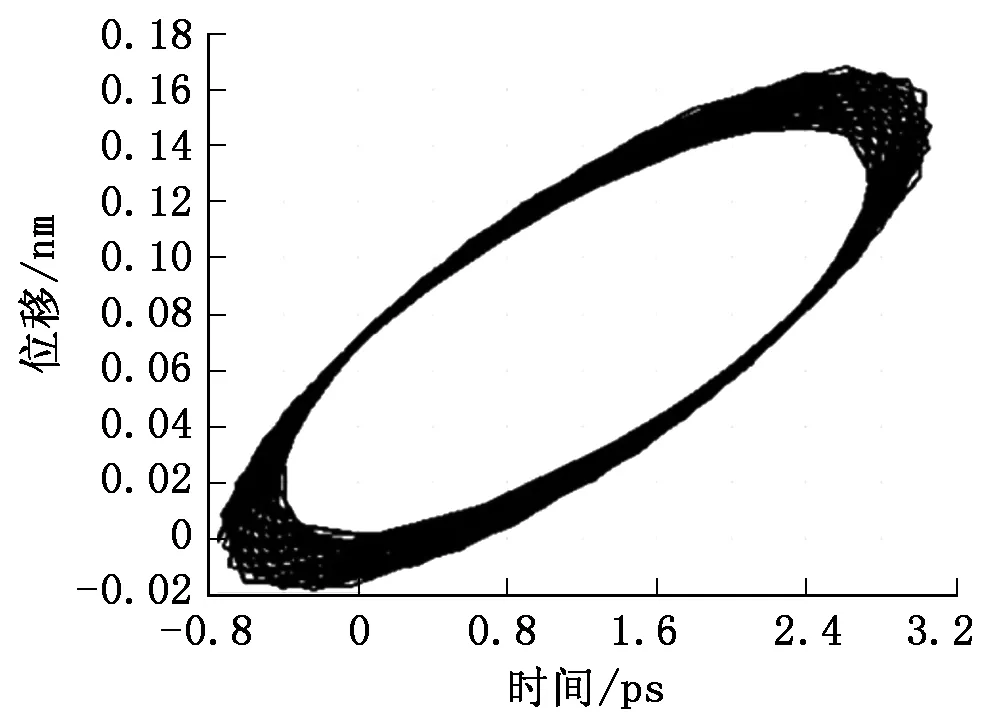
图6 刀尖椭圆运动轨迹图

3.3 振子的谐响应分析

切削装置振子的振幅的量级是微米级别的，振子的振动状态会极大影响到被加工零件的表面粗糙度。设置振子谐响应的频率在27.1 kHz～28.3 kHz，经过ANSYS进行分析可以获得振子的导纳曲线以及导纳圆图，分别如图7、图8所示。振子在不同频率的导纳数值对于振子以及超声波电源制作有一定参考价值。

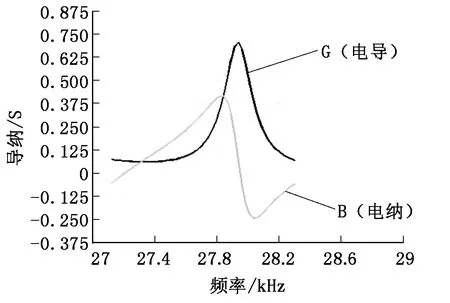
图7 振子的导纳曲线图

图8 振子的导纳圆图

4 结束语

基于切削装置振子的结构动力学分析得到的模态、瞬态以及谐响应分析结果，可以确定所设计的切削装置振子是合理的，在理论研究上是可以实现椭圆切削加工的。所设计的振子可以实现模态转化，在振子的刀尖处复合出椭圆振动的轨迹。本文研究可为振子的实际制作提供可靠的参数。