带箱约束的非线性全局优化问题降维算法研究①
王晓霞
(齐齐哈尔大学理学院,黑龙江 齐齐哈尔 161000 )
0 引 言
随着社会科技、经济的迅速发展,全局最优化问题经常出现在经济模型、金融、图像处理、环境工程学等方面[1]。全局优化是优化领域的重要内容,全局优化发展是指通过对最优点的研究,找出最优点特性、最优点寻找途径,并以此为目的组织算法,研究该算法的性质和实际效果提取[2-3]。传统的非线性规划易陷于局部最优解,很难得出全局最优化的解,降维是处理维数较高空间问题的有力措施[4-5]。其中三角函数降维能够有效地降低目标函数维度,在其将n维空间函数转换为一维空间函数后,得到的一维函数具备较强波动性,通过遗传算法对一维问题进行求解[6]。求出来的一维问题的解即为多维空间问题的全局最优解的近似解。本次研究在进行带箱约束的非线性全局优化问题降维算法研究时,应从约束函数角度出发,给定与约束函数紧密联系的降维形式,找出约束下降维参数与致密度的联系,以降维曲线长度估计计算量,最终提出理论算法。
1 以降维方法求解带箱约束的非线性全局优化问题
1.1 降维变换及其性质
最优化问题的一般表达式为minf(x),s.t.cj(x)=0,j∈E,cj(x)≤0,j∈I其中x∈Rn为决策变量,f(x):Rn→R、cj(x):Rn→R分别为目标函数、约束函数,集合X={x|cj(x)=0,j∈E;cj(x)≤0,j∈I;x∈Rn)}是相应最优化问题的可行域。指标集由E={1,2,...,L}、I={p+1,p+2,...,m}进行表示,点x处的紧约束以I(x)={j,cj(x)=0,j∈I∪E}进行表示。研究通过基于降维的全局优化近似算法,对带箱约束的非线性全局问题进行优化求解。并且在区间[0,π]范围中构建降维公式,给出降维曲线的α-致密度后,根据降维曲线长度验证该近似算法[7]。
x1=rcos(θ),x2=rsin(θ)
(1)
利用阿基米德曲线以θ相关函数对r进行表示,可得r=αθ,α>0,θ>0。式(1)转化为x1=αθcos(θ),x2=αθsin(θ)。研究将利用此三角函数类型作为降维曲线。本质上来讲,降维指通过空间填充曲线得到近似可行域,从而简化目标函数的变量数目,达到将多变量简化为单变量的目的。降维假设空间Rn中,至少存在一点y∈X⊂Rn可以令d(x,y)≤α,即称集合X在空间Rn中α-致密。
d(x,y)=
(2)


图1 α-致密曲线的具体构造算法
h:D→X,θh(θ)=(h1(θ),h2(θ),...,hn(θ))
(3)
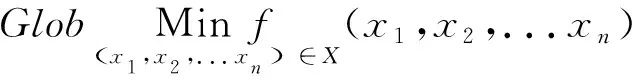

H:[a,b]→RntH(t)=
(h1(t),h2(t),...,hn(t))
(4)
式(4)中H表示定义在区间[a,b]上的参数曲线,将[a,b]分成n个子区间。
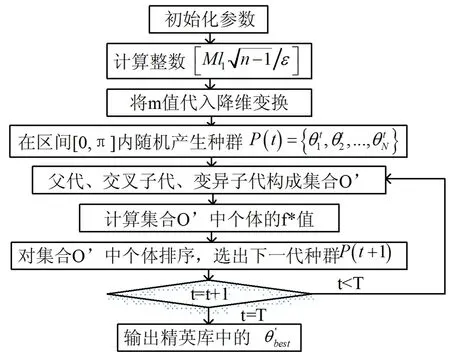
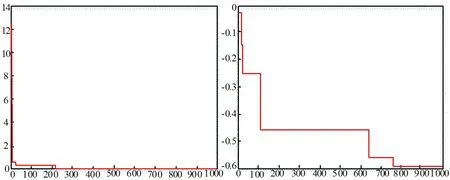
a=t0 (5) 使Ht0,t1,...,tn成为一条过点Pi=H(ti)=(h1(ti),h2(ti),...,hn(ti))的折线,长度为Ln=L(Ht0,t1,...,tn),则可知曲线H的长度L(H)存在时,其应为Ln=L(Ht0,t1,...,tn)的上确界。当H:[a,b]→Rn、H∈C1([a,b],Rn)时,曲线H的长度存在。 (6) limm→S'=Mn-1c (7) γ∈U(-1,1),γ≠0 (8) 适应度函数可取函数本身,即fit(θ)=f*(θ),令父代为θ1,θ2,式(8)则为交叉子代的表达式。通过变异概率Pm判断个体变异的需求,选择一个个体,产生(0,1)间的随机数,当变异概率不小于随机数时,变异子代的表达式为: (9) 式(9)中λ~N(0,1),Δθ~N(0,σ2)。基于降维的箱约束优化近似算法的具体步骤如图2所示。 图2 基于降维的箱约束优化近似算法 研究将采用数学软件MATLAB R2017b对基于降维的箱约束优化近似算法进行数值模拟,并将之取得的结果与原函数本身的精确最优解作出比较。选择六个算例,执行基于降维的箱约束优化近似算法,在将之降维成一维函数后,执行遗传算法。 图3中横纵坐标分别为算法的迭代次数、每代的精英函数值。可知每一代精英个体的目标函数值均随着迭代次数的增加而减少,算例1最终收敛至0,算例2最终收敛至-0.2。 图3 算例1、2精英函数值随着迭代次数的变化情况 算例3: 10.1[(x2-1)2+(x4-1)2]+ 19.8(x2-1)(x4-1),s.t.- 2≤xi≤2,i=1,2,3,4 算例4: minG(x1,x2,...,x6)= 算例3中参数N取400,T取1000,Pc取0.9,Pm取0.2,可得最小值点θ*的值为0.79207,全局最小值f*(θ)的值为0.00413419。算例4中参数N取600,T取1000,Pc取0.9,Pm取0.35,可得最小值点θ*为1.53741,全局最小值f*(θ)为-0.59131344。 图4中横纵坐标分别为算法的迭代次数、每代的精英函数值。可知每一代精英个体的目标函数值均随着迭代次数的增加而减少,算例3最终收敛至0,算例4最终收敛至-0.6。 图4 算例3、4精英函数值随着迭代次数的变化情况 算例5: 算例6: s.t.-1≤xi≤1,i=1,2,...,40。 对二者执行基于降维的箱约束优化近似算法,在将之降维成一维函数后,执行遗传算法。算例5、算例6中参数一致,N取600,T取1000,Pc取0.9,Pm取0.1。可得算例5的最小值点θ*为0.99446,全局最小值f*(θ)为-0.98856804,算例6的最小值点θ*为0.94743,全局最小值f*(θ)为-0.96549770 图5中横纵坐标分别为算法的迭代次数、每代的精英函数值。可知每一代精英个体的目标函数值均随着迭代次数的增加而减少,算例5、算例6最终均收敛至-1。 图5 算例5、6精英函数值随着迭代次数的变化情况 表1中θ*表示f*(θ)最优点,min指f*(θ)最优值,Global min表示标准算例最优值。由表1可知,研究采用的基于降维的箱约束优化近似解法具备有效性;同时在数值效果方面,低维的函数拥有更高的精度。 表1 函数的数值实验结果 研究通过三角函数对带箱约束的非线性全局优化问题进行降维变换,将多维函数转换为一维函数,随后利用遗传算法对一维函数进行处理。研究结果表明,随着迭代次数的逐渐增加,每一代精英个体的目标函数值逐渐减小;六个带箱约束的非线性全局优化问题的算例中,原函数本身的精确最优解与基于降维的箱约束优化近似解法相比,二者解出来的值基本一致。也就是说,以一维问题的最优解得出原n维箱式约束问题最优解的近似。综上所述,实验采取的基于降维的箱约束优化近似解法是科学有效的,其能在保证精确率的前提下,成功降低问题难度;同时,在数值效果方面,低维的函数拥有更高的精度。研究虽然取得了一定成就,但在多目标多维全局优化问题上仍有进一步探讨的必要,希望随着了解更多的α-致密曲线,未来能够推广三角函数降维曲线的应用范围。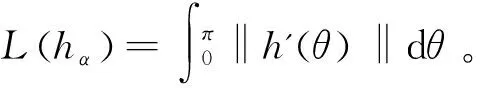
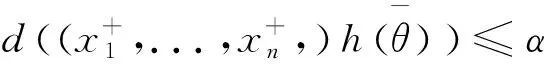
1.2 算 法

2 实验与分析

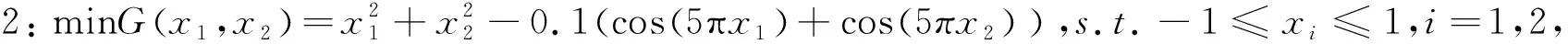

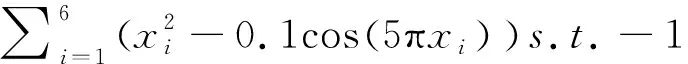


3 结 论

