不同截面形式下的钢管轴压临界载荷影响因素分析①

张 芹, 李雨城, 王 伟

(安徽三联学院机械工程学院，安徽 合肥 230601)

0 引 言

钢结构在实际工程中应用广泛，其发展过程从最初的强度刚度验算到结构稳定性计算[2]。现今随着材料科学的发展，钢结构趋于轻型薄壁化，更易发生失稳破坏，结构稳定性验算[3]是设计关键。结构失稳类型分为极值点失稳，分支点失稳两类，极值点失稳理论计算更贴近实际。基于此种问题，本文建立实际工程中应用最广泛的两种钢管模型，对比分析在不同参数下的构件承受轴压载荷时的屈曲载荷及力学响应。

1 欧拉临界应力

基于分支点失稳理论，假定理想直杆无初曲率，载荷无初偏心，其临界屈曲载荷[4]描述为：

式中:左端项Pcr为临界屈曲载荷，E为钢管弹性模量，I为钢管截面惯性矩；L为构件轴向长度。按照小挠度理论得出的随遇平衡状态能得出正确的临界载荷，但是大挠度理论下，考虑变形二阶效应能得出精确结论。

2 数值计算

2.1 模型工况

圆钢管模型内径495mm，轴向长度1000mm，壁厚5mm，方钢管模型内边长990mm，壁厚5mm,轴向长度1000mm，钢材弹性模量210×105MPa，泊松比0.35。模型网格如图1和图2所示：

图1 圆钢管模型网格划分图

图2 方钢管模型网格划分图

2.2 网格划分，边界条件及计算

有限元模型采用3D壳单元建立，正六面体网格，采用扫略法划分网格；线性摄动分析步求解线性屈曲，上下两端口面建立关键点耦合自由度。最终计算所得线性屈曲模态如图3所示：

图3 圆钢管线性屈曲模态

基于线性屈曲分析结果，添加关键字进入inp文件进行非线性屈曲分析，采用通用分析步，继续细化分析步，增大迭代次数以达到计算收敛，圆钢管非线性屈曲应力云图如图4所示：

图4 圆钢管非线性屈曲应力云图

3 钢管屈曲参数对比分析

参数分析

有限自由度体系的稳定计算主要有静力法与能量法[5]，从理论计算的角度来看，能量法能得出更为精确的结果，应用范围也较广；数值计算中的有限元方法可以考虑影响薄壁构件屈曲载荷[6]的各个参数作用。

考虑不同壁厚对屈曲载荷Pcr的影响：

表1 不同壁厚下的钢管屈曲载荷Pcr

方钢管与圆钢管在考虑不同壁厚时，其临界屈曲载荷对比曲线:

4 结 论

1)轴压作用下两类钢管模型临界屈曲载荷数值结果与理论计算值误差在合理范围内，第二阶段的非线性屈曲分析过程记录了构件变形过程，验证了有限元模型计算结果的可靠性。

2)钢管构件壁厚的增大，对于薄壁钢管构件临界屈曲载荷时均有较大提升作用，但壁厚增大对结构稳定性提升的贡献率呈递减趋势，实际应用应综合考虑其他因素，确立壁厚值。

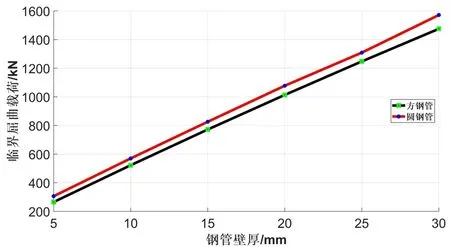
图5 不同壁厚方钢管与圆钢管临界屈曲载荷对比曲线

3)钢管构件耗材量相同时，相较于方钢管，当截面形式选取为圆形后将显著提升结构在轴压作用下的临界屈曲载荷；相应的当薄壁钢管构件具有相同的抗屈曲能力时，选用圆形截面将使得耗材更少，有限材料下取得更大的截面惯性矩，具有较好的经济性。