垃圾填埋场稳定性影响因素重要性分析①
崔广强, 陈士海
(1.华侨大学土木工程学院,福建 厦门 361021; 2.福建江夏学院工程学院,福建 福州 350108)
0 引 言
随着城镇化建设的发展和人民生活水平的提高,城市生活垃圾的产量急剧增加,垃圾填埋场的建设受到越来越多的关注与重视。垃圾填埋场建设的首要问题是稳定,其失稳破坏的事故在国内外均有发生,造成严重的后果[1]。因此,对垃圾填埋场的稳定性研究具有重要的实际应用价值[2]。不少学者对垃圾填埋场的稳定性进行了研究,研究表明其稳定性的影响因素很多[3~7],例如,垃圾土的物理化学性质,衬里的类型,衬里与垃圾或土壤之间的剪切特性,垃圾填埋场的几何特征,渗滤液的高度和垃圾分解产生的气体存在状态与迁移以及垃圾填埋场的建设、施工、运营等。其中垃圾填埋场内的渗滤液水位对垃圾填埋场的稳定性有至关重要的影响,渗滤液在填埋体内的集聚,其水位会不断的升高,伴随孔隙水压力的增加,导致土体及衬垫界面处的抗剪强度降低,可能引起边坡的失稳破坏[8,9]。而关于渗滤液高度对填埋体稳定性影响的程度和其他因素的对比分析尚未见有正式论文的发表。
本文充分考虑渗滤液高度对垃圾填埋场稳定性的影响,借助正交试验和BP神经网络,分析九个因素的变化对稳定性的影响,找出主次要影响因素,对稳定性分析提供一些有意义的理论依据。另一方面,垃圾填埋场的不稳定性通常是由多种因素共同影响,但在一某些条件下,可能只有一种或几种起主要影响作用。各种因素的影响程度也决定了不稳定的机制与方式,所以研究各因素的影响程度,可以有针对的给予重视或关注以提醒工程建设采取必要的工程措施。最后,通过敏感性分析区分主要和次要因素,这有利于垃圾填埋场工程建设的反分析并对工程设计和试验方案进行优化提供参考依据。
1 正交试验设计和BP神经网络
1.1 正交试验设计
正交试验设计[10]是指研究多个因素和多个水平的试验设计方法。基于正交性,从综合测试中选择出其中具有代表性的数据作为代表点,选出的这些代表点均匀分散,整齐可比。正交试验设计是采用组合理论推导进而形成正交表安排试验的主要方法。当研究三个或跟多影响因素,并且这些因素之间可能存在相互作用时,计算分析的工作量将成倍的增加,有时可能难以实现。为了减少计算工作量应对这种困境,正交试验设计是一个很好的解决方法是正确的选择。正交试验设计依靠组合理论得到的正交表的正交性,从试验所列实验数据中选出一些代表点进行试验设计,并且可以用最少的试验或计算次数,系统分析等同于全面试验的效果。因此正交表试验设计具有高效、快速而及经济且能够分析多因素等优点,值得推广。文中利用计算极差的方法分析了各影响因素对稳定性影响的程度,分析了不同影响因素对安全系数的变化趋势, 将各影响因素的影响程度进行了排序,得出意义的结论和进一步的研究方向。
1.2 BP神经网络方法
人工神经网络是简单神经元组成误差逆传递的互联网络,其可以进行模拟生物神经系统与真实世界的相互作用。它不仅具有通用的计算能力,并且还能够通过学习和记忆来推理所获得的知识,并具备很大的非线性映射能力。被应用最广泛的人工神经网络是误差逆传播神经网络,称之为BP网络[11,12],BP神经通常由一个输入层、若干个隐藏层和一个输出层组成,如图1所示。实践证明,三层BP神经网络可以满足绝大多数函数的映射或拟合问题。

图1 三层神经网络学习
图1中小圆圈表示神经元,x1,x2,…,xn为输入信号,即输入的数据,yi为输出信号。其中,输入层有n个节点,对应于BP神经网络有n个输入;隐藏层包含m个节点,对应于BP神经网络中的m输出响应,输出层只有1个节点。根据特定的分析问题来确定输入层和输出层中的节点数,并且可以不同的选择每层中的神经元的数量。在常用的神经网络中一般的对应关系是m=2n+1(m为隐藏层中神经元的数量,n是输入层中神经元的数量)。通过权重调整层间的节点,其中隐藏层中的神经元的数量是不定数,并且神经元之间的转换传递函数通常使用Sig-moid函数。网络学习与训练的基本原则是通过不断修改网络权重和阈值来减少沿负梯度方向的误差[13]。BP神经网络的学习过程主要由四部分组成:(a)输入模式顺传播;(b)输出误差逆传播;(c)循环记忆训练;(d)学习结果的判断。
BP神经网络可以解决输出和输入之间的任意复杂的非线性映射问题,并且已广泛应用于边坡工程中[14],扩大该方法在岩土工程其它领域的应用是国内外学者关注的课题。
2 采用的计算分析方法
将渗滤液高度作为垃圾填埋场稳定性的一个重要影响因素,讨论了渗滤液不同高度作用下填埋场的滑移破坏的安全系数,采用双楔体法[9]验算填埋场的滑移稳定性,计算见图图2所示。

图2 填埋场双楔体法分析图
在分析垃圾填埋场稳定性时,安全系数是确定垃圾填埋场是否稳定的一个重要指标,因此被视为系统特性。垃圾填埋场稳定性影响因素的影响程度是在影响因素变化的前提条件下,安全系数FS变化的幅度(极差)。
计算公式:
η=(FS0-FS1)/FS0×100%
式中,FS0为影响因素未改变时的安全系数;FS1为影响因素发生某一改变时的安全系数;η为安全系数变化的百分数。
选择9个影响因素:填埋体渗滤液面的高度、填埋场的高度和宽度、垃圾体的填埋坡角、垃圾体的重度、垃圾土的内摩擦角、垃圾土的粘聚力、复合衬垫层之间的最小摩擦角及最小粘聚力。利用前述的3层BP神经网络,预测填埋场滑移破坏稳定性的安全系数,输入层为9个影响因素,中间层单元的数量为2*9+1=19,使用线性激活的函数输出安全系数作为输出层。本文所使用的9-19-1的三层BP神经网络结构(如图1所示)。
3 填埋场稳定性影响因素分析
3.1 工程算例
工程实例:某卫生填埋场[15]:垃圾体渗滤液面高度为3m,垃圾土的重度为rsw=10.2 kN·m-3、垃圾土的内摩擦角φsw=30°、垃圾土的粘聚力csw=3kPa, 复合衬垫层之间的最小摩擦角δln=18°和最小粘聚力cln=4kPa,填埋场的高度H=30m, 宽度B=20m, 角度α=14.036°。
BP 网络进行训练,经过30 步学习收敛,精度达0.01,训练好的网络确定输入和输出层之间的权重和阈值。
3.2 计算结果分析
在文中,双楔体法用于计算安全系数,计算模型如图2所示。根据传统的单因素分析方法,采用双楔体法计算不同因素不同水平作用下的安全系数。 分析所考虑的因素和因素水平取值见表1所示。采用双楔体法计算9个因素单独改变时,各因素在不同水平下的安全系数如表2 所示。根据表1的水平将填埋场9个因素进行组合,形成56组样本,将这56组样本输入训练好的BP神经网络,输出的安全系数见表3所示。

表1 影响因素和水平
为了研究各因素影响程度与传统方法的对比,根据表3和56组样本组合情况,计算每个影响因素的每个水平的安全系数试验结果的平均值,并列于表4中。不同水平同一因素的安全系数平均值的最大值与最小值之差称为该因素变化所对应的安全系数的极差,极差的大小表现为该因素影响安全系数的程度(重要性)。从表2和表4中的计算结果可以看出,尽管两种方法的极差不同,但其排序先后顺序一致,说明每个因素的重要性是一致的,并且由于正交试验和BP神经网络充分考虑了多因素共同作用的影响是符合实际的,也充分证明了该方法的实用性。
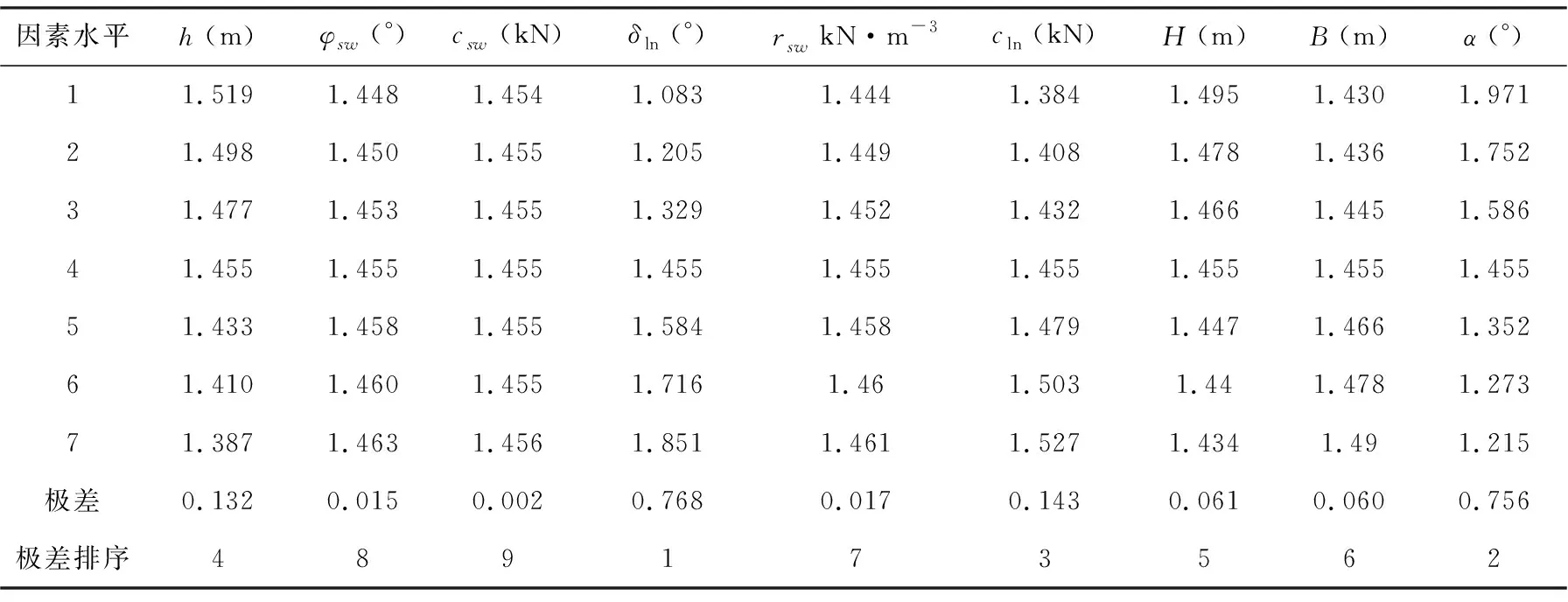
表2 单因素变化所对应的安全系数

表3 正交试验结果表
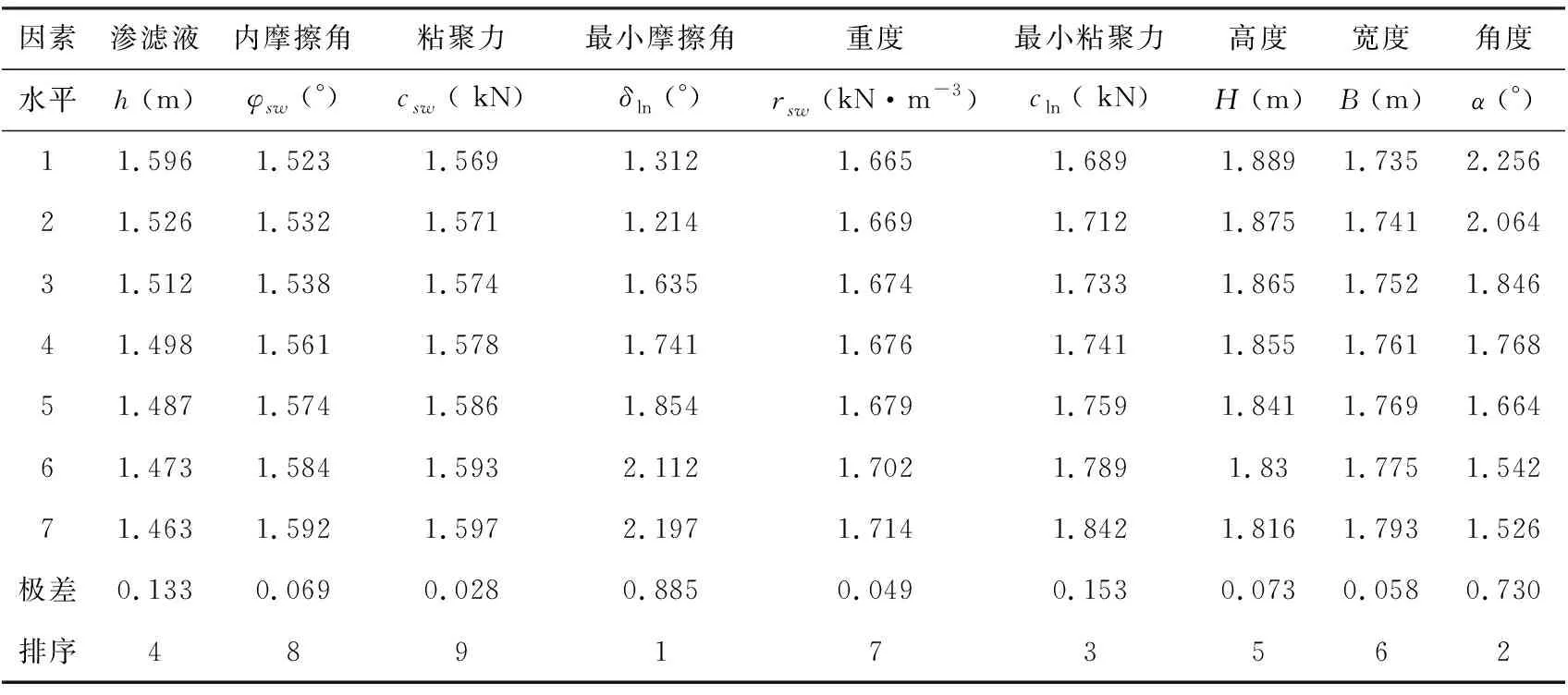
表4 安全系数正交试验结果汇总表
4 结 论
(1)所考虑的9个影响因素对卫生填埋场滑移破坏的影响程度依次排序为:δln(°)>α(°)>cln(kN)>h(m)>H(m)>B(m)>rsw(kN·m-3)>φsw(°)>csw(kN)。其中,复合衬里层之间的最小摩擦角δln、垃圾体的堆填坡角α、垃圾体的最小粘聚力cln和渗滤液面的高度h为主要影响因素,它们在填埋场稳定性方面起主要作用,其他因素是次要影响因素。
(2)渗滤液面高度的影响程度排位第4,表明了渗滤液高度对填埋场稳定性的影响有很大的作用,在其他的论文中没有表述,分析计算填埋场稳定性时应给予充分的考虑。
(3)填埋场各因素取值的确定受所用材料、施工工况和填埋情况的影响而不同,需要研究相应的试验方法去确定,应该改变传统的土工试验仪器与试验方法综合分析与计量。
(4)渗滤液高度的确定受多种因素的影响,需要研究填埋体的组成成分和其持水率等因素,在今后的试验与研究中,应加强该方面的收集与整理。
(5)所使用的正交试验设计与BP神经网相结合的方法,考虑了多种因素同时变化对安全系数影响,与传统的单因素方法分析的因素影响程度一致,证明了该方法的实用性。而该方法更符合工程实际情况,覆盖面广,计算准确性高,可以在类似工程中推广应用。

