浅窄内河航道船舶航行下沉量试验研究
缪吉伦,吴俊,李晓飙,王云莉
(1.重庆交通大学西南水运工程科学研究所,重庆 400016;2.重庆西科水运工程咨询中心,重庆 400016)
0 引言
航行在浅窄航道中的船舶,由于河底和岸壁的存在,会受到浅水效应和岸壁效应作用,加剧了船舶航行的不安全因素。当船舶驶入浅水限制性水域后,由于船底水下间隙变小,原来在三维空间中运动的水体只能在二维平面内流动,同时流速增大,致使压力剧烈变化,且压力波动范围进一步扩至船尾,因而在兴波增大的同时,船体愈加下沉。浅水中的船体下沉及纵倾变化较之深水更为激烈,对船舶操纵影响较大,甚至产生船底擦碰河底造成搁浅事故。目前针对内河船舶在限制性航道中的下沉量研究成果较少。随着内河船舶日趋大型化、高速化,水上交通日益繁忙,船舶在限制水域中航行,发生碰撞、搁浅等海难事故的危险性也更大。GB 50139—2014《内河通航标准》[1]中没有关于限制性航道设计水深的计算公式,只规范了最小取值。JTS 165—2013《海港总体设计规范》[2]中给出了海港进港非限制性航道中船舶航行时船体下沉量与船舶吨级、航速之间的关系,但对于内河航道尚未给出明确规定。因此,研究浅窄限制性航道中的船舶航行下沉量对于保证船舶航行安全具有十分重要的意义。
1 国内外研究现状
国内外针对船舶航速、航行阻力、船行波以及航行下沉量与航道尺度等因素之间的关系,进行了模型试验、数值计算以及原型观测等系列研究,取得了一些研究成果。关于船舶下沉量的研究,Tuck等提出了一系列估算下沉量的经验公式,但主要适用于海船及宽敞的浅水水域[3]。俞湘三等[4]根据能量方程和连续性方程,提出了限制性航道船周回流与船体下沉的计算公式。沈鸿玉等[5]研究了按照一元定常流动理论,推导了运河矩形断面航道的回流速度。郑宝友等[6]通过限制性航道船舶航行试验,研究了500 t和300 t船队航行时的船周回流速度与船体下沉,提出了交错航行时的船尾下沉量是渠道水深设计的控制条件。李焱等[7-8]通过物理模型试验,研究了IV、V级航道的升船机中间渠道的航行水力特性,提出了中间渠道相应的参考尺度及其确定原则。吴澎等[9]结合国内外相关规范和设计手册,对比分析了各种船舶航行下沉量的计算公式,探讨了限制性航道大型船舶下沉量计算公式适用范围。目前国内有关研究主要是针对某一具体工程,研究较为分散,缺乏普适性,尚无完善的内河船舶下沉量的具有实用价值的研究成果。
2 航行下沉量经验公式
当船舶在航道中运动,水流受边界条件的影响产生阻塞效应,形成回流,水流受挤压,船首压力高,产生壅水现象,船尾压力较低吃水增大,形成船体下沉。影响船舶航行下沉量的因素包括:1)边界条件,如航道断面尺度、河床底质、断面形式和断面系数等。2)船舶条件,如船型及尺度,方形系数,船体粗糙度,船舶编队队形等。一般来说,船舶的方形系数越大,航行时的下沉量越大。3)运动要素,如船舶(队)的航速、水流流速流态等。4)水体物理特性,如水体密度、运动黏性系数等。5)其他,如船舶交会、风浪的影响等。当边界条件、船舶尺度型线确定后,船舶航行下沉量主要与航速、航道尺度和回流流速等有关。基于试验研究及观测资料,一些学者研究提出了以下船舶下沉量经验公式。
2.1 Barrass公式(1981)
1981年,Barrass根据实船试验及模型试验成果,归纳得出船舶在开敞水域和受限水域的船首下沉量的计算公式[3]:

式中:ΔT为船舶航行下沉量,m;CB为船舶方形系数;Vk为航速,kn;c为回流速度系数,c=ΔV/V=S/(1-S)。其中:ΔV为回流速度,m/s;V为水流速度,m/s;S为阻塞比。
式(1)可计算非限制性和限制性航道内的船舶航行最大下沉值,适用水深吃水比h/T为1.1~1.4,阻塞比S为0.10~0.25,船舶方形系数CB为0.5~0.85,船舶航速Vk为0~20 kn。其中:h为航道水深,T为船舶吃水。
2.2 Yoshimura公式
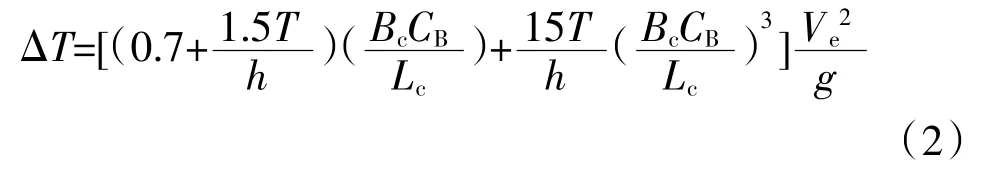
该公式对非限制性和限制性航道等都适用[3]。式中:Ve为修正速度,对于限制性航道取V/(1-S)。其中:Lc为船长,m;Bc为船宽,m。
2.3 Huuska-Guliev公式(1976)

式中:Cs=2.4;为排水量,=CB·Lc·Bc·T;Frh为;Ks为修正系数,对于限制性航道当阻塞比S>0.03时,Ks=7.45S+0.76;当S≤0.03时,Ks=1.0。适用水深吃水比h/T为1.2~2.0,船舶方形系数 CB为 0.6~0.8,Lc/Bc为 5.5~8.5[3]。
2.4 Eryuzlu公式(1978)
1978年,Eryuzlu等在3艘有球鼻艏的VLCC油船模型试验的基础上,得出船首下沉量的计算公式[10]:

式(4)适用水深吃水比h/T为1.08~2.78,船舶方形系数CB≥0.8的VLCC船型。
2.5 Millward公式(1990)
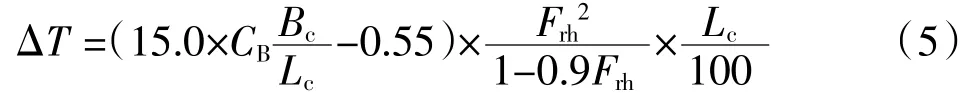
式中各参数意义同前。适用水深吃水比h/T为 1.25~6.0 的各种船型[11]。
3 试验
3.1 模型试验
上述公式大多基于海船研究得出。内河船舶尺度更小、吃水浅,航行水域更窄,水体密度小,上述公式不适宜内河船舶,本文通过模型试验开展了内河船舶下沉量研究。试验船型采用3 000吨级货船,船型尺度86.8 m×16.2 m×3.5 m(船长×船宽×吃水),方形系数0.837。Z形试验数据K'=1.812,T'=0.586。为了保证船体制作精度,采用3D打印技术进行船体构造[12]。
室内试验概化模型为正态,比尺为1∶30,按重力相似准则设计,模型全长30 m,渠道断面为矩形。模型边壁和底部采用钢化玻璃制作,模型两端安装消波网,以减小水波反射对船模运动的影响。水位/波浪采用UBL-2超声波水位/波浪测量系统进行测量,无线旋桨流速仪测量船周回转流速,在船模航线上设置1个激光测距传感器,测量船模下沉量。沿渠道模型顶部布置1套船舶航行多参量测量系统,对船舶航行速度与漂角进行测量。将二维倾角传感器安装在船模重心,测量船模运动过程中的横倾与纵摇。
试验测试了3 000吨级货船单船不同渠道宽度、航速、水深工况下船舶航行参数。1)断面宽度:32.40 m、40.50 m、52.65 m、56.70 m、60.75 m、64.80 m;2)水深:3.4 m、3.9 m、4.4 m、4.9 m;3) 航速:1.09 m/s、1.92 m/s、3.34 m/s;共计 6×4×3=72种工况。此外也采用1 000吨级货船试验测试了以下工况组合船舶航态变化。1)断面宽度:50 m、55 m、60 m、70 m;2)水深:3.2 m、3.5 m、3.8 m、4.1 m;3) 航速:1.67~3.33 m/s共7档。模型试验主要参数见表1。

表1 模型试验主要参数表Table 1 Main parameters ofmodeltest
3.2 试验成果分析
模型试验开展了船舶下沉量、船周流速及船舶阻力测试。模型试验结果表明:1)随着船舶航速增大,下沉量也增大,但当渠道底宽逐渐缩小到某一宽度时,下沉量趋于稳定。2)随着渠道宽度和水深加大,船舶下沉量呈减小趋势,渠道底宽的影响比水深的影响更显著,这与此前一些学者对海船的研究是基本一致的。3)一般说来,船舶在断面系数较小的航道中航行,将在浸水断面上产生显著的回流。回流引起的水位降低远较在开阔水域中航行时显著。但本试验中下沉量和断面系数之间没有明显的规律,数据分布比较杂乱。
试验成果与Barrass等经验公式计算结果对比见图 1(a)~图 1(e)。
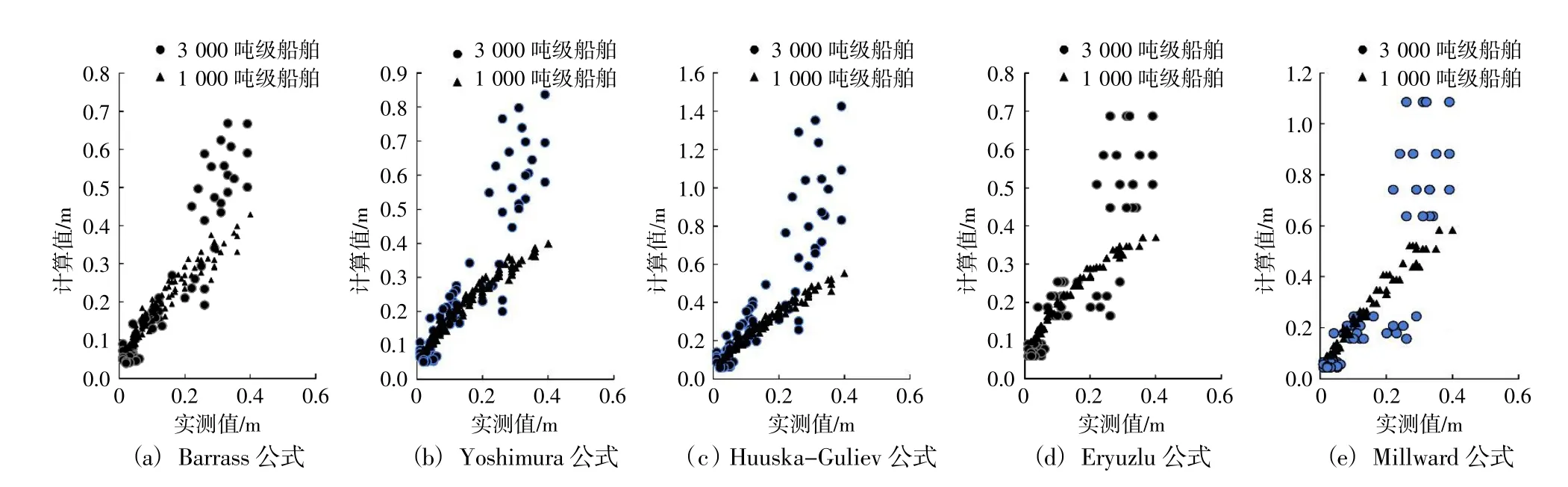
图1 下沉量实测值与公式计算值对比图Fig.1 Comparison ofmeasured value and empiricalformula value ofsinkage
从图1得出,Barrass公式计算下沉值与实测值相关系数R=0.89,Yoshimura公式相关系数为0.86,Huuska-Guliev公式相关系数为0.82,Eryuzlu公式相关系数为0.86,Millward公式相关系数为0.87。总体来看,Huuska-Guliev公式偏差最大,Barrass公式相关度较好且计算值与实测值最接近。Barrass公式形式简单,考虑了船舶方形系数、航速、阻塞比等主要因素的影响,可以此作为内河船舶下沉量计算公式,但计算值较实测值偏大。考虑到该公式基于海水条件下试验得出,内河条件下根据实测值改进如下:

改进后的Barrass公式计算值与实测下沉量对比见图2。从图2看,改进后的Barrass公式计算值与实测值更加吻合,均匀分布在45°斜线附近。

图2 下沉量实测值与改进Barrass公式计算值对比图Fig.2 Comparison ofmeasured value and improved Barrass formula value ofsinkage
为验证所提出的船舶下沉量近似计算公式的有效性,采用本文所示3 000吨级船舶计算了在不同水深、不同速度条件下的最大下沉量,计算值与试验值对比见图3。
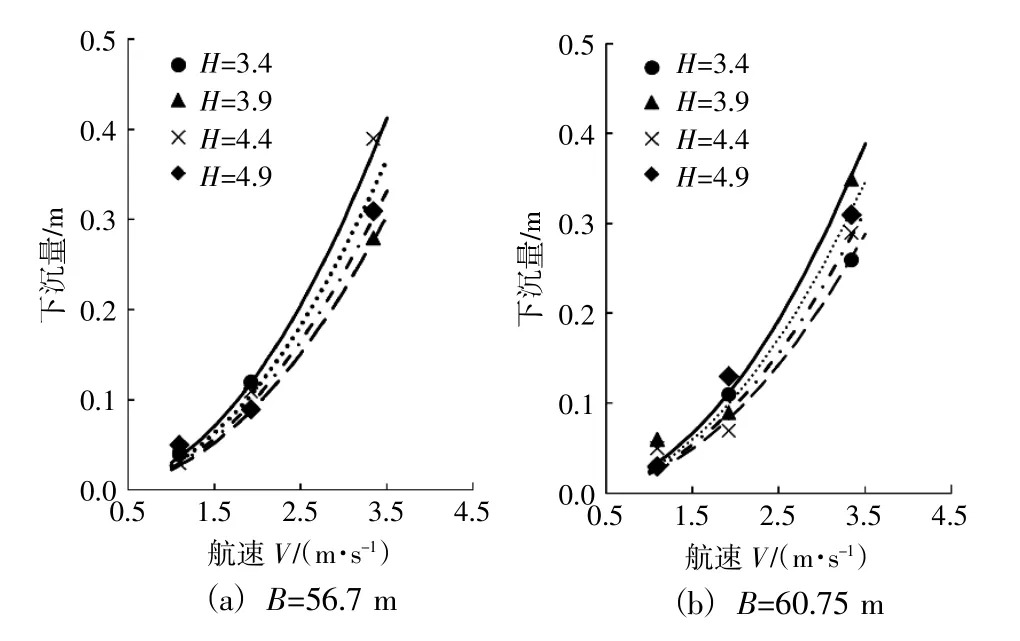
图3 不同宽度和不同水深时下沉量实测值与计算值对比图Fig.3 Comparison ofmeasured and calculated sinkage values with differentwidth and depth
从图中可以看出,计算结果与试验结果吻合良好,除少量工况外,误差均小于5%。由此可知,所提出的船舶最大下沉计算公式是合理的,对分析船舶下沉量及航道富裕水深具有很好的参考价值。
4 结语
船舶航行下沉量是航道水深设计的重要考量因素,随着内河船舶的大型化发展,精确计算浅窄限制性航道中船舶航行的下沉量对提高航道改造经济性、保障船舶航行安全具有重要意义。
我国现行的《海港总体设计规范》中给出了船舶航行下沉量与船舶吨级及航速之间的关系,但对于内河航道尚未给出明确规定。限制性航道宽度狭窄,断面系数小,船舶航行时的浅水效应明显,下沉量加大,但现有研究对内河限制性航道下沉量研究较少。本文通过概化物理模型,研究了内河限制性航道中1 000~3 000吨级船舶在不同渠道宽度、水深及航速条件下船舶航行的下沉量。分析了影响下沉量的主要因素,应用经验公式与实测下沉量进行了对比分析,提出了适合内河船舶的下沉量计算公式,该公式具有较高的计算精度,能够满足航道改造工程设计对船舶航行时估算船舶最大下沉量的要求。

