基于响应面法的电驱动桥结构优化设计

潘运平，方 闹，吴昌权，廖烈平

(1.武汉理工大学 机电工程学院，湖北 武汉 430070；2.湖北车桥有限公司，湖北 荆州 434300)

汽车驱动桥是车辆传动系统的重要环节，同时也是汽车重要的承载件，其结构和性能直接影响驾驶时的安全性和操控性，对汽车驱动桥的优化设计一直是汽车领域的研究热点。王强[1]等利用响应面近似模型对驱动桥最大应力和疲劳寿命进行优化，俞云云[2]等构建了驱动桥壳的Kriging模型，采用多目标优化方法对桥壳质量进行优化，赵来杰[3]对电动车同轴一体化电驱动桥进行了有限元分析并进行轻量化设计，Park[4]等证明了基于计算机辅助的代理模型技术在结构优化设计上的可行性，Ping[5]等采用构建代理模型的方法对汽车进行了轻量化研究。

笔者以电动车平行式电驱动桥为研究对象，将有限元法与响应面法相结合，构建了驱动桥静强度、刚度和质量与驱动桥结构参数之间的近似函数关系，通过求最优解实现驱动桥的轻量化。

1 数值模拟试验模型构建

为了得到响应面函数，需要进行多次试验获取样本点响应值，采用实体试验研究成本过大，因此采用有限元数值模拟方法对驱动桥进行仿真分析是一种较为可行的方法。

1.1 电驱动桥结构与基本参数

所研究的电驱动桥结构如图1所示，由于电机和减速器采用平行布置方式，因此驱动桥壳为非对称结构。

图1 电驱动桥结构示意图

对电驱动桥进行受力分析，首先需要获取电驱动桥相关参数，各参数如表1所示。

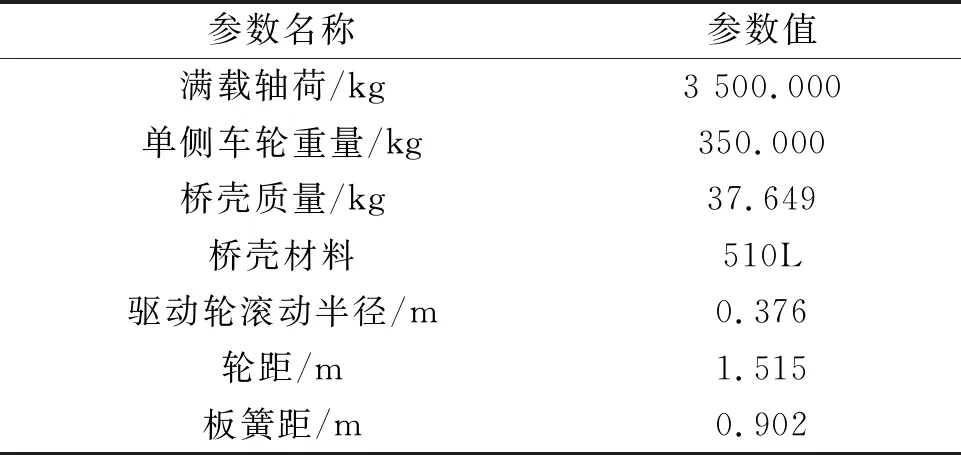
表1 电驱动桥相关参数

1.2 电驱动桥强度计算

驱动桥的静强度分析通常分为4个极端工况[6]进行研究，这里以驱动桥最大垂向力载荷工况为例，分析该工况下驱动桥的应力与位移特性。最大垂向力载荷工况下驱动桥受力如图2所示，根据受力图可以判断桥壳危险截面在板簧座处。

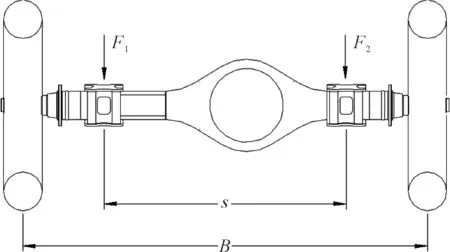
图2 最大垂向力载荷工况下驱动桥受力情况

最大垂向力载荷工况下，桥壳受到满载轴荷和最大垂向力载荷的共同作用，这时，桥壳上两个板簧座上的载荷F1和F2可以表示为：

(1)

F0=kd·G

(2)

式中：G为满载轴荷；F0为最大垂向力载荷；kd为动载荷系数，这里取为1.5。

于是可以转化为如下关系：

(3)

由此可以计算得到桥壳板簧座出的弯矩为：

(4)

式中：gw为单侧车轮(包括轮毂制动器)的重量；B为轮距；s为板簧距。

如图3所示，对驱动桥截面做了去除圆角的简化处理，驱动桥桥壳板簧座处截面各尺寸为：δ=0.006 m，B=0.106 m，b=0.094 m，H=0.106 m,h=0.094 m。

图3 驱动桥截面尺寸参数

由此可以计算得到驱动桥危险截面处的弯曲应力为：

(5)

(6)

式中：σw为驱动桥危险截面处的弯曲应力；Wv为危险截面处的截面弯曲系数。

1.3 电驱动桥有限元分析

首先对电驱动桥三维模型进行简化，删去了结构中的非承载件，最终得到如图4所示的有限元分析模型，对有限元模型进行网格划分，设置网格尺寸为3 mm，通过网格划分得到553 939个单元，2 213 579个节点，网格模型如图5所示。

图4 驱动桥有限元模型

图5 网格划分模型

设置驱动桥最大垂向力载荷工况下的边界条件，如图6所示。A代表最大垂向力载荷工况下的载荷大小F=85 750 N，B代表电机和减速器对桥壳产生的负载F1=2 940 N，C和D代表轴管受到的轴承支撑约束。

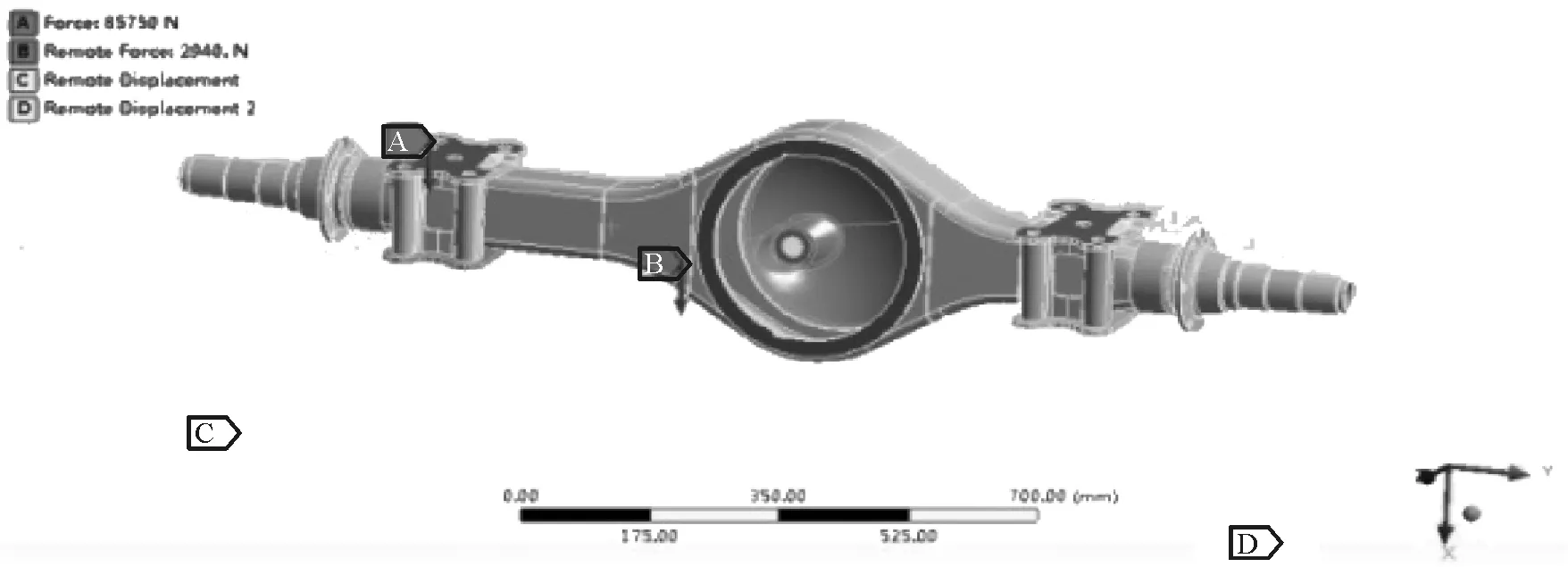
图6 有限元模型边界条件

经过有限元分析计算得到最大垂向力载荷工况下驱动桥的应力和位移分布云图如图7和图8所示，由图7和图8可知，驱动桥最大应力在桥壳与板簧座交界处，最大应力为171.62 MPa，与理论计算结果非常接近，说明有限元模型具有较高的准确性，驱动桥最大位移为1.004 7 mm。

图7 驱动桥壳应力云图

图8 驱动桥壳位移云图

2 试验设计

建立驱动桥静力学有限元分析的模型后，利用该模型进行各样本点下的数值模拟分析，通过响应面法构建驱动桥目标函数与设计变量之间的函数关系。

2.1 目标函数和设计变量的选择

在构建响应面函数之前，首先需要选择目标函数和设计变量，设计变量应尽可能选择对目标函数影响较大的参数进行研究[7]。笔者选择3个目标函数进行研究：电驱动桥最大垂向力载荷工况下对应的最大应力Y1、电驱动桥满载轴荷工况下的变形量Y2、电驱动桥的质量Y3；选择的设计变量为：桥壳方形截面的外圆角半径x1、桥壳截面厚度x2、桥壳上下表面距离x3、桥壳左右表面距离x4、桥包中心距桥壳过渡截面的距离x5。桥壳设计变量示意图如图9所示。

根据驱动桥零部件之间的配合约束关系确定了变量各自的变化范围如表2所示。

2.2 试验样本点设计

本次试验采用中心复合设计[8]获取试验样本点，各变量对应的样本点分布情况和标准化编码以后的样本形式如表3所示，将有限元模型的尺寸值修改为各样本点对应的实际尺寸值，利用修改后的三维模型进行有限元分析，获得每个样本点对应的响应值，部分试验数据如表4所示。

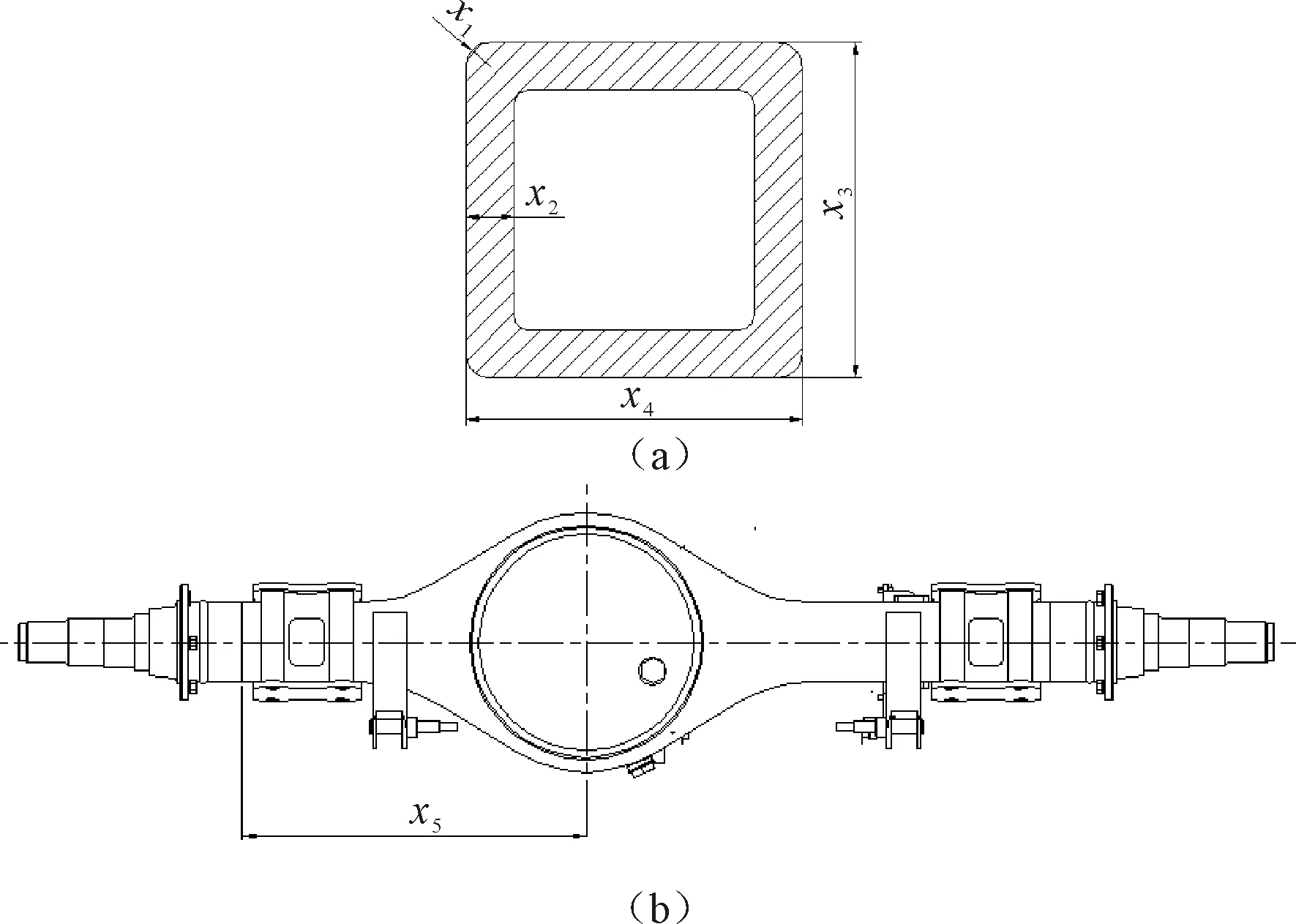
图9 桥壳设计变量

表2 设计变量变化范围

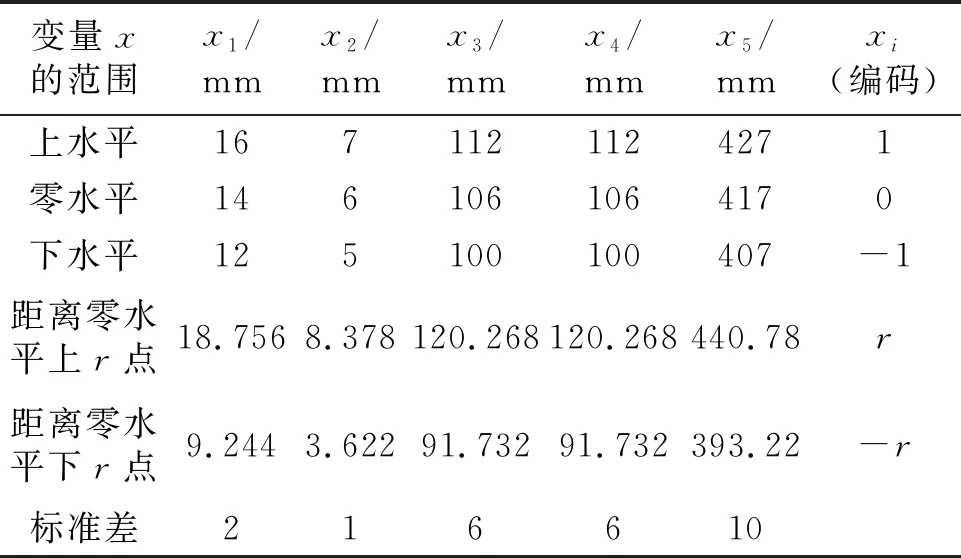
表3 样本点分布

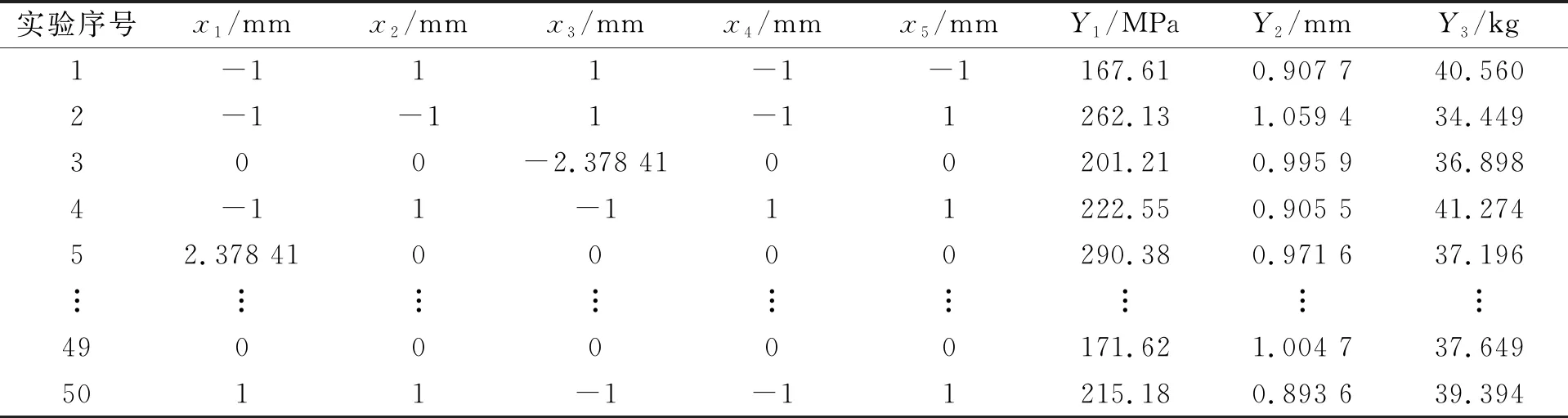
表4 部分样本点及响应值

3 试验结果分析

3.1 获取响应面函数

响应面法的目的是通过多项式来拟合试验中的样本数据[9]，响应面函数的标准形式如下:

(7)

式中：β0为回归系数；k为变量个数；ε为模型误差；βi、βii、βij为回归系数；xi、xj为自变量。

利用响应面分析软件Design-Expert对试验数据进行处理，拟合得到各响应面函数的表达式如下：

(9)

(10)

3.2 函数精度分析

各目标函数的响应面函数的理论预测值与样本实际值的分布情况如图10～图12所示，从图10～图12可以直观地看到函数的拟合效果。

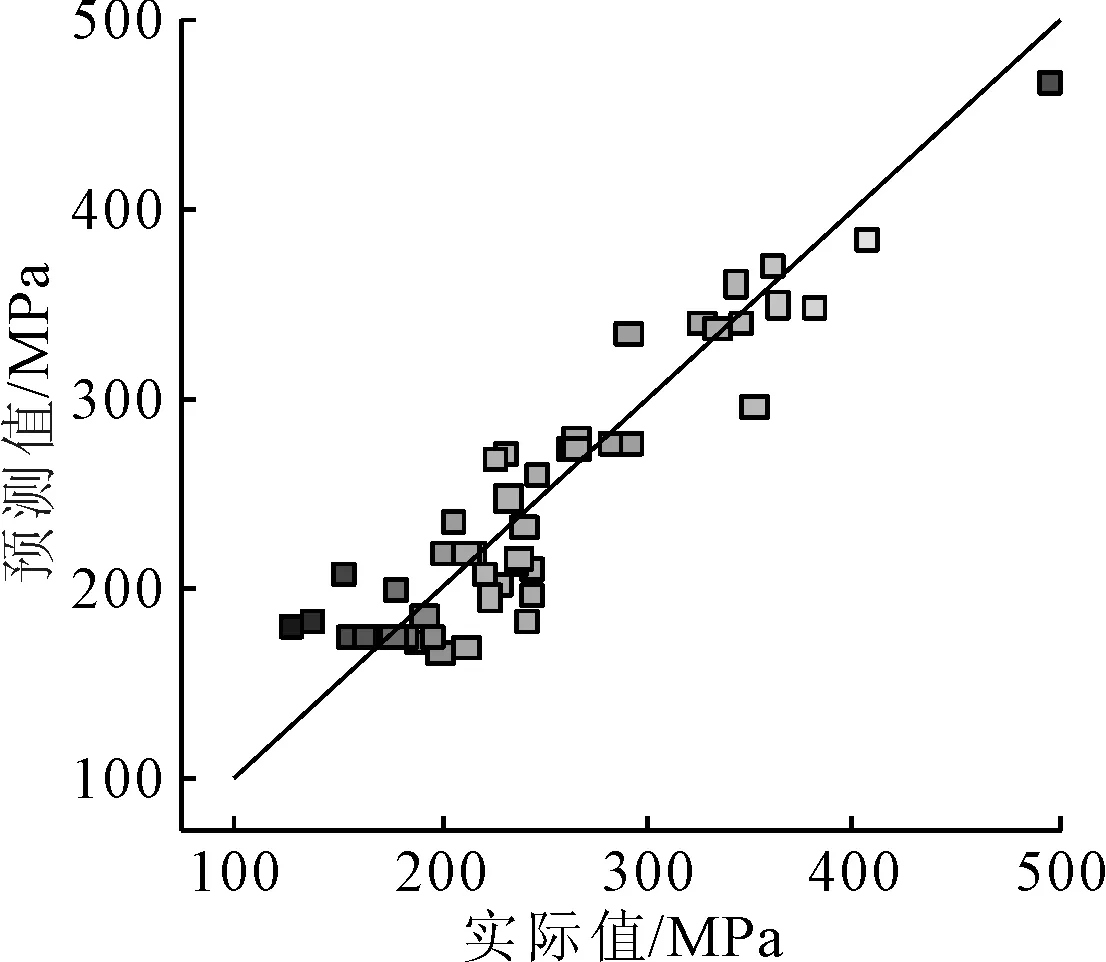
图10 桥壳应力Y1实际值与预测值分布情况

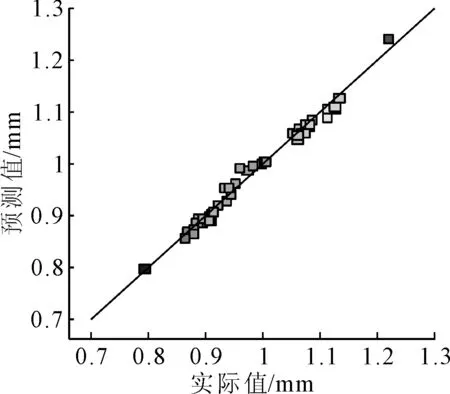
图11 桥壳变形Y2实际值与预测值分布情况

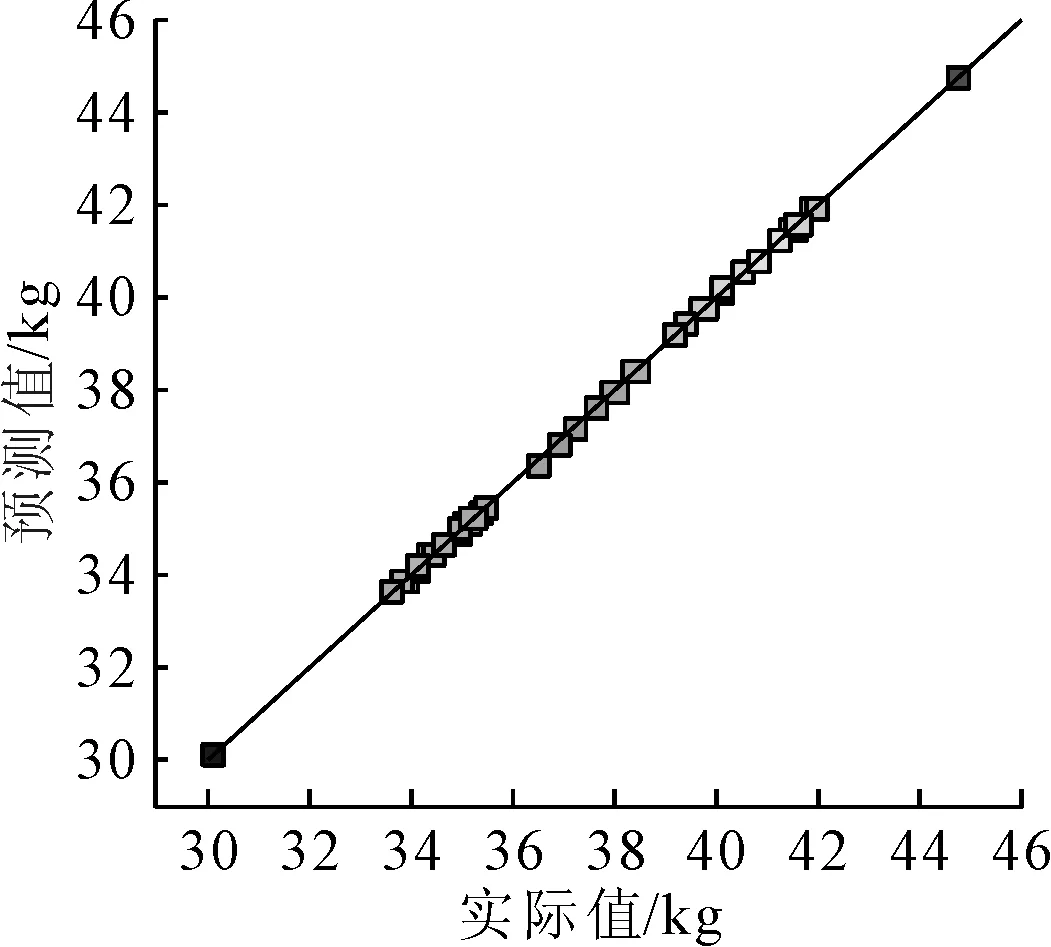
图12 桥壳质量Y3实际值与预测值分布情况

表5 函数精度评价指标

4 优化设计

利用得到的响应面函数模型对驱动桥进行优化设计，以桥壳的质量Y3为优化目标，桥壳的最大应力和最大位移为约束条件，其中根据汽车驱动桥台架试验标准要求[10]，满载轴荷时每米轮距变形量不超过1.5 mm，驱动桥轮距为1.515 m，由此可知驱动桥最大变形量不超过2.27 mm，对驱动桥的垂直弯曲强度取安全系数为2进行约束。 驱动桥的优化目标为:

minY3

(11)

约束条件为：

(12)

式中：i=1,2,3,4,5；Y1为桥壳应力;Y2为桥壳变形;Y3为桥壳质量。

通过优化计算，得到以驱动桥质量最低为优化目标的最优解,如表6所示。

表6 最优解对应的变量值

将最优解对应的尺寸参数输入到有限元模型进行求解，得到最优解对应的有限元分析结果,如表7所示。

表7 最优解对应的响应值

有限元分析的应力和位移云图如图13和图14所示，由优化结果可以看出，经过优化的桥壳最大应力分布在板簧座附近，最大位移在桥壳中段，优化后的桥壳满足强度和变形要求，优化后整体质量由37.649 kg减少到36.241 kg,减重率为3.74%。

图13 优化桥壳应力云图

图14 优化桥壳位移云图

5 结论

笔者基于响应面方法构建了驱动桥应力、位移和质量与驱动桥结构参数之间的近似函数关系，以驱动桥质量最小为优化目标，优化后驱动桥的减重率达到3.74%，且优化后的驱动桥强度和刚度满足要求。以近似数学模型代替传统有限元模型进行优化计算，大大降低了计算量，其研究方法和结论可为电驱动桥的设计和优化提供思路。