湖南省资水流域汛期暴雨气候特征分析

李兵，文强，章新平，杨令，刘电英，杨乐清

（1.湖南省益阳市气象局，湖南益阳 413000；2.湖南师范大学资源与环境科学学院，长沙 410081）

0 引言

我国幅员辽阔，地形地貌复杂多变，是全球气象灾害发生次数最多的国家之一，暴雨灾害作为最常见最主要的一种气象灾害，不仅能直接造成山洪、城乡内涝，也能衍生滑坡、泥石流等地质灾害，严重威胁到人民群众生命财产安全，因此对暴雨的短期天气预报与中长期气候趋势预测是当前气象服务的重中之重。湖南省水系发达，雨水资源丰富，是我国暴雨灾害最严重的省份之一，全省暴雨主要集中时段在春末至夏初、其次是盛夏至初秋[1]。2000年来厄尔尼诺现象频发，湖南省暴雨发生频率有上升趋势；据全省地面气象观测站数据，资水流域中游的全省暴雨中心安化大暴雨事件发生频率显著上升，2010—2017年安化国家基本气象站连续8 a 出现了大暴雨事件，2019年暴雨日高达9 d。

【研究进展】关于我国暴雨时空变化特征的分析，国内许多科研工作者做了大量的研究工作，如史培军等[2]分析了全国659个气象站1951—2010年日降水量资料，发现我国年代际暴雨雨量、暴雨日数、暴雨雨强均呈增加趋势，暴雨有从东南沿海向华中、西南地区扩张的趋势。戴泽军等[3]利用线性趋势法分析了1960—2013年湖南省88个台站暴雨时空分布特征，结果表明湖南省区域暴雨日数、暴雨强度、整体有增加趋势。周亮广等[4]分析了1951—2009年淮河流域44个气象站日降水量资料，发现淮河流域暴雨

雨量有明显增加趋势，暴雨雨量较大地区暴雨集中度偏高，暴雨雨量较小地区暴雨集中度偏低。【切入点】暴雨的空间、时间集聚是造成大范围洪涝灾害的重要原因之一，然而关于暴雨时空变化的研究定性分析的研究相对较多[3,5-6]，关于暴雨时空聚集程度、出现概率等方面的定量研究相对较少，而这正是短期天气预报和中长期气候趋势预测关心的重点。【拟解决的关键问题】为了进一步改善湖南省暴雨的短期天气预报以及中长期气候趋势预测服务，以湖南省资水流域为例，利用经验正交函数（EOF）分解、空间自相关分析（Moran’s I 指数）、Mann-Kendall 检验、线性倾向估计法、累积距平法分析了1980—2016年湖南省资水流域汛期（4—9月）暴雨日数、暴雨量、暴雨集中度（PCD）、集中期（PCP）时空分布及演变特征，同时基于Γ 分布和“雨日-无雨日”一阶Markov链模型从理论上定量计算了流域14个国家气象站汛期10、20、30 d 内出现暴雨的概率，【研究意义】研究结果对掌握资水流域雨水资源时空分布，做好湖南省资水流域暴雨的短期天气预报、中长期气候趋势预测、流域防灾减灾等工作具有一定的指导作用。

1 资料与方法

1.1 资料

采用湖南省气象信息中心提供的经过严格质量控制后的湖南省资水流域 14个国家气象站1980—2016年逐日降水量资料，数据准确可靠，流域国家气象站分布与流域位置图如图1、图2所示。前1 天20:00 时至当天20:00 时的累积降水量为当天日降水量，若日降水量≥0.1 mm，则该日为一个雨日，否则该日为无雨日，根据雨日前天是否为雨日，分为初始雨日和连续雨日，分别统计其雨日样本。

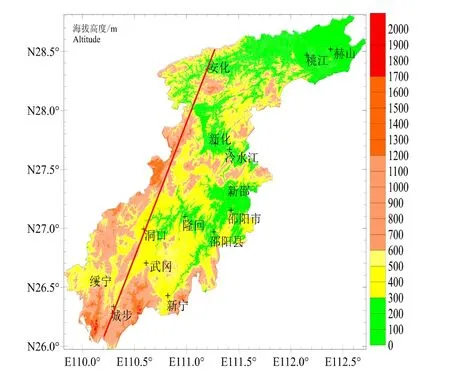
图1 资水流域国家气象站分布图Fig.1 Spatial distribution of national meteorological observatory over Zishui river basin

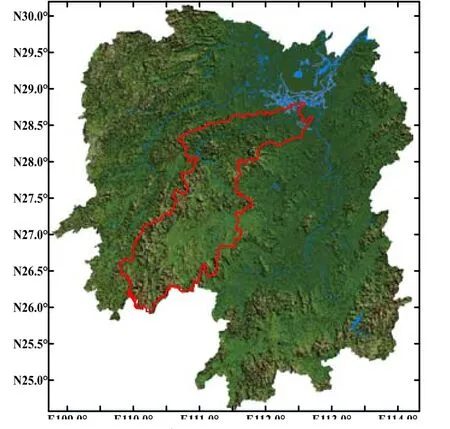
图2 资水流域位置图Fig.2 Location map of Zishui river basin in Hunan province

由于资水流域覆盖范围相对较小，各地气候特征无显著区别，因此仍采用中国气象局日降水量＞49.9 mm为暴雨的定义，统计1980—2016年4月1日—9月31日各气象站暴雨日数、暴雨量（暴雨日日降水量总和）。

1.2 方法

利用经验正交函数（EOF）分解[7]、全局Moran’sI指数[8-9]、线性倾向估计[7]、Mann-Kendall 检验[7]等方法分析暴雨日数、暴雨雨量、暴雨平均集中度、暴雨平均集中期的时空分布与变化特征；根据数理统计理论，基于“无雨日-雨日”演变的一阶Markov链模型[10-12]，利用Γ 分布计算各气象站汛期10、20、30 d 内出现暴雨的概率。上述方法相关文献有详尽介绍，现仅对全局Moran’s I 指数、“无雨日-雨日”演变的一阶Markov 链模型简要介绍如下。

1.2.1 全局Moran’s I 指数

某区域单元的暴雨日数和暴雨雨量往往和其临近区域单元关系密切，空间自相关分析能定量讨论二者之间的这种相关程度，全局型自相关指数能定量衡量其空间分布的差异性与相关性。

全局Moran’s I 指数范围值为-1～1，正值表示暴雨日数、暴雨量空间分布具有正相关性，负值表示具有负相关性，0值表示空间相关性不明显，其计算式为：

式中：m为气象要素场格点数；Fi为气象要素在第i个格点的值；为气象要素平均值，wij为气象要素场在第i，j两格点之间连接关系。Moran’s I 指数的相关性分析是否成立，需要用Z-score 得分来检验，Z-score 计算式为：

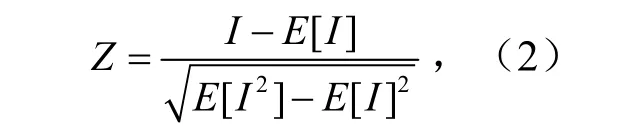
式中：E为各量数学期望值，当∣Z∣＞1.96 时，说明在95%的概率下，气象要素场存在空间自相关性，Z得分的绝对值越大，空间自相关性越显著。1.2.2 无雨日-雨日演变一阶Markov 链模型

假设日降水量概率分布与前1 天是否有雨相关，无雨日、雨日的{(Jn-1，Xn)，n=1，2，3，...}演变过程符合一阶Markov 链模型，该过程可以用一个双变量随机过程描述，即，当Jn-1=0 时表示该天是无雨日，Jn-1=1为雨日，Xn是第n天的日降水量。Jn和Xn的起始序号分别为0 和1。

对于Jn-1=0 首次雨日和Jn-1=1的连续雨日这2种情况，假设日降水量Xn都服从Γ 分布，其概率密度函数为：

式中：i=0，1 分别对应首雨日和连续雨日，αi＞0，βi＞0分别为Γ 分布的形状参数和尺度参数，x为日降水量（mm）。

第n天的日降水量≤x的条件分布函数可由概率密度函数积分得到：

N天内最大降水量过程写为{Mn：n=1，2，3，...，N}，其中Mn=MaxXi为N天内最大日降水量，Mn的条件分布函数为：

式中：i=0，1 时分别为初始日为无雨日、雨日的情况。为了得到日最大降水量概率分布函数，由全概率公式计算：

式中：P[J0=0]，P[J0=1]为初始概率，而Gn(x,0)和Gn(x,1)可由递推公式得到：

式中：其中P00、P01、P10、P11为转移概率，可由站点逐日降水量统计得到，满足P00+P01=1、P10+P11=1。得到概率分布函数后便可计算其出现暴雨的概率。

2 湖南省资水流域汛期暴雨时空分布特征

2.1 流域年均暴雨日数、暴雨量空间分布

图3为湖南省资水流域1980—2016年汛期年均暴雨日数、暴雨量空间分布图，由于站点数目有限，空间插值方法采用径向基函数插值法，仅简单考虑了山脉走向造成的各向异性。由图3可知，流域年均暴雨日数最大的站点为安化站，高达5.4 d，最小的站点为城步站，仅为1.9 d。流域年均暴雨日数空间分布十分不均匀，其等值线走向与山脉走向大体一致。

年均暴雨量空间分布与年均暴雨日数分布高度类似，最大的安化站440.9 mm，最小的城步站137.1mm。年均暴雨日数大的站点，其年均暴雨量值也大，反之亦然。进一步的分析表明，年均暴雨量与暴雨日数显著正相关，其线性相关系数高达0.9899。

图3 湖南省资水流域年均暴雨日数、暴雨量空间分布图Fig.3 Spatial distribution of average rainstorm days and heavy rainfall over Zishui river basin during flood season

资水流域的地形能显著地影响天气系统的发生、发展，使得暴雨分布表现出明显的中小尺度特征[13]。图4给出了平均暴雨日数、海拔高度、地形坡度的“西南—东北”向的截面曲线，截线如图1中红实线所示。结合流域地形地貌特征，不难发现处于山脉迎风坡、湖区山区过渡地带的、地形起伏相对较大的站点暴雨日数、暴雨量相对较大，处于盆地、山脉背风坡的站点其值相对较小。基于径向基函数插值法得到的流域年均暴雨日数（暴雨量）空间分布图不能完全反映出流域不同地区的差异，更精细的暴雨日数、暴雨量空间分布图依赖于分布更广的区域气象观测站观测资料以及空间插值方法的改进。

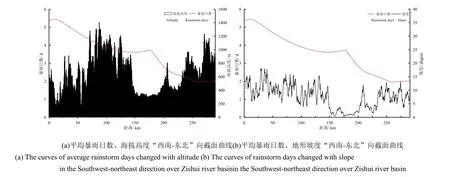
图4 湖南省资水流域平均暴雨日数、海拔高度、地形坡度截面曲线Fig.4 The curves of rainstorm days changed with altitude and slope in the Southwest-northeast direction over Zishui river basin

2.2 流域暴雨日数、暴雨量EOF分解

经验正交函数（EOF）分解可对气象要素场进行时、空分解，提取其主要的空间分布特征[7]，由于该方法不受气象要素场偏态分布的影响，故在气候诊断分析中应用广泛。各站点暴雨日数、暴雨量EOF分解第1、第2 特征向量空间分布如图5所示，其中图5（a）、图5（b）分别为流域暴雨日数EOF分解第1、第2 特征向量特征值空间分布图（第1、第2 特征向量特征值贡献率分别为36.9%、16.8%，为最主要的2个特征值），图5（c）、图5（d）分别为暴雨量EOF分解第1、第2 特征向量空间分布图（特征值贡献率分别为38.1%、18.5%）。其余特征值没有通过95%置信度检验，在此不予讨论。

图5 湖南省资水流域暴雨日数、暴雨量EOF分解前2个特征向量空间分布图Fig.5 The two main modes of EOF for rainstorm days and heavy rainfall over Zishui river basin

由图5可知，流域暴雨日数、暴雨量EOF分解主要存在全局（整体偏大或偏小）型、南（偏多或偏少）北（偏少或偏多）型；全局型虽然整体表现为偏多或偏少，但各站点距平百分率差别明显，年均暴雨日数较大的站点的距平百分比相对较大，距平百分比在20%以上，最高可达43%；而年均暴雨日数较小的站点的变率相对较小，距平百分率在20%以下，最低仅为8%。说明年均暴雨日数较小的站点气候预测难度较小，年均暴雨日数较大的站点气候预测难度较大，也更容易发生偏涝或偏旱。

统计EOF分解时间系数，表1给出了模态1、模态2 出现年份数，由表1可知1980—2016年37 a 中，暴雨日数EOF分解模态1 出现了17 a，暴雨量EOF分解模态1 出现了23 a，说明全局型确实是其主要模态，全局型中又以全局偏少为主。

表1 湖南省资水流域暴雨日数、暴雨量EOF分解 主要模态年份数统计Table1 Years of two main modes of EOF for rainstorm days and heavy rainfall over Zishui river basin

2.3 流域暴雨日数年际变化趋势与突变分析

利用线性倾向估计分析流域各气象站点汛期暴雨日数线性变化趋势，作出了其线性趋势空间分布图，如图6（a）所示。

图6 湖南省资水流域汛期暴雨日数气候倾向分布图与M-K检验曲线Fig.6 M-K test curves of rainstorm days of different streams over Zishui river basin

流域平均暴雨日数、暴雨量存在增加趋势，平均暴雨日数气候增长率为0.1 d/10 a，平均暴雨量气候增长率为13.1 mm/10 a，但二者没通过95%的概率检验。流域14个气象站有9个暴雨日数存在增加趋势，5个存在减少趋势，由于暴雨日数的年际振荡，其线性变化趋势并没通过95%概率的统计检验。为了进一步分析暴雨日数年际振荡中是否存在突变节点，利用M-K检验作出了流域上、中、下游1980—2016年汛期平均暴雨日数的统计量UFk和UBk曲线，如图6（b）、图6（c）、图6（d）所示，其中点线为临界曲线（表示当UFk、UBk绝对值大于1.96 时，在95%的概率下其存在明显增加或减小趋势）。结合累积距平曲线，可知流域平均暴雨日数存在明显突变节点，其突变节点在1987年前后，1987年之前为暴雨日数偏少时期，1987年之后为暴雨日数偏多时期，是20 世纪90年代表现为显著偏多，地域上中下游偏多更加明显。

2.4 流域暴雨日数、暴雨量空间自相关分析

由式（4）、式（5）计算了1980—2016年各年代平均暴雨日数、暴雨量全局Moran’s I 指数与Z得分值，如表2所示。

表2 湖南省资水流域气象站各年代平均暴雨日数、 暴雨量全局Moran指数与Z得分统计Table2 Universal Moran’s I、Z score of rainstorm days and heavy rainfall over Zishui river basin

由表2可知，20 世纪80年代流域暴雨日数（暴雨量）相对偏少时，暴雨日数（暴雨量）空间分布具有随机性，没有明显表现出大值（小值）空间聚集分布的特征；20 世纪90年代后流域暴雨日数（暴雨量）相对偏多，其空间分布具有明显的聚集分布特征，尤其是20 世纪90年代暴雨日数、暴雨量显著偏多时期，暴雨日数（暴雨量）空间分布具有明显的正相关性，且通过了95%概率检验，南北两极分化特征十分显著。这说明，在流域暴雨发生次数偏少时，流域暴雨空间分布具有随机性，当流域暴雨发生次数整体偏多时，流域暴雨空间分布具有两极分化特征，暴雨日数多的站点暴雨发生次数比平均更多，暴雨日数少的站点暴雨发生次数比平均更少。

2.5 流域暴雨集中度、集中期变化特征

根据周亮广等[4]暴雨集中度（PCD）、集中期（PCP）的定义，计算了流域各气象站1980—2016年平均暴雨集中度、集中期，其结果如表3所示，图7为流域平均暴雨集中度、集中期年际变化曲线。

表3 湖南省资水流域各气象站汛期暴雨集中度、集中期统计Table3 PCD、PCP of heavy rain of each meteorological observatory over Zishui river basin during flood season

图7 流域平均暴雨集中度、集中期年际变化曲线Fig.7 Varying curves of average precipitation concentration degree and precipitation concentration period of heavy rain

由表3 分析可知，流域暴雨日数、暴雨量较少的上游地区暴雨集中度相对较小，平均集中度为0.82，其平均暴雨集中期为6月26日；流域暴雨日数、暴雨量较多的中游地区暴雨集中度也相对较小，其平均集中度为0.83，其暴雨集中期最早，为6月21日；流域下游暴雨集中度相对较大，平均值为0.86，集中期最晚，为6月29日。

对于全流域而言，汛期平均暴雨集中度为0.82，平均暴雨集中期为6月26日，流域平均暴雨集中度、集中期有明显的年际变化，线性倾向估计表明，流域暴雨集中度存在增加趋势，暴雨集中期则存在提前趋势。

结合湖南省汛期气候特征，梅雨期间，中国东部雨带由华南整体北抬至长江中下游一带，受地形特征的影响，湖南省资水流域最先发生暴雨的往往不是流域南部的上游地区，而是流域中游的冷水江、安化，这进一步说明地形因子影响流域暴雨天气系统发生、发展、移动的重要因素。

3 湖南省资水流域汛期30 d 内暴雨发生概率计算

汛期暴雨时空分布相对集中，为了定量计算流域各气象站汛期若干日内发生暴雨的概率，基于1.2 小结的相关方法，利用Γ 分布从理论上计算了流域14个气象站汛期10、20、30 d 内最大日降水量概率密度分布函数、最大日降水量概率分布函数，各站点暴雨发生概率如表4所示。

表4 湖南省资水流域气象站汛期30 d内暴雨发生概率Table4 Probability of heavy rain for meteorological observatory over Zishui river basin in 30 days during flood seasons

由表4可知，汛期20、30 d 内暴雨发生概率空间分布情况与平均暴雨日数、暴雨量空间分布类似，平均暴雨日数、暴雨量大的站点，发生暴雨的概率也相对较高，反之亦然，30 d 内发生暴雨概率最高的为安化站，概率为46.0%，最低的为城步，概率为20.4%；就全流域而言，汛期10 d 内暴雨发生的平均概率为12.4%，20d 内暴雨发生的平均概率为23.1%，30d 内暴雨发生的平均概率为32.2%。

为了解流域汛期30 d 内最大日降水量概率密度分布特征，以流域暴雨中心安化为例，图8给出了安化站的概率密度分布曲线与累积概率曲线。

可知，10 d 内最大日降水量概率密度变化较为复杂，概率密度曲线存在一极小值和极大值，概率密度先随降水量的增加而减小，达到某极小值后，概率密度随降水量增加而增加，增加达到某极大值后，又随降水量的增加而减小，这表明10 d 内出现日降水量小于1 mm的天气概率最大。20、30 d 内最大日降水量概率密度变化相对简单，只存在一极大值点，概率密度先随降水量增加而增加，达到极大值后随降水量增加而减小，这表明20、30d 内发生暴雨的概率逐步增加。

进一步对比分析表明（图略），平均暴雨日数较大的气象站，在概率密度曲线极大值左侧，其值较小，在极大值右侧，其值较大；对于概率曲线，平均暴雨日数较大的气象站，其概率随降水量的增加减小趋势不明显，其概率曲线更加扁平。综上，平均暴雨日数较大站点的概率密度更加分散，概率曲线更加扁平，出现暴雨以上降水的概率更大；而平均暴雨日数较小的气象站，其概率密度分布更加集中，出现中雨以下弱降水的概率更大，出现暴雨以上降水的概率较小。

图8 湖南省资水流域代表站点30 d内最大日降水量概率密度分布曲线与概率曲线Fig.8 The probability and probability density curves of maximum daily precipitation in certain days of representative meteorological observatory over Zishui river basin

4 讨论

众所周知地形是影响暴雨日数（暴雨量）空间分布的重要因素，本文的研究表明地形对暴雨集中期和集中度也有较大影响，目前关于地形坡度、地形坡向、地形遮蔽度等因素对暴雨集中度、集中期的定量影响研究相对较少，这都是值得进一步研究的课题。

相对以往湖南省暴雨气候特征分析的研究[3,5]，本文得到的资水流域汛期暴雨空间自相关系数、EOF分解特征向量场、暴雨集中度、集中期、出现概率等定量结果对进一步做好湖南省资水流域汛期暴雨预报服务将更具实际参考作用。

本文只基于Γ 分布计算了汛期30 d 内最大日降水量概率，虽然对Γ 分布与其他分布函数的拟合优度没有比较分析，但得到的暴雨发生概率空间分布与流域年均暴雨日数的分布特征高度一致，这说明基于Γ分布计算暴雨发生概率是可取的。资水流域汛期暴雨主要集中在6月，基于Γ 分布得到的汛期30 d 内各气象站暴雨概率对汛期内暴雨空间分布特征把握较好，但没有体现出暴雨概率在各个月份的差异，有待改进。

5 结论

1）1980—2016年湖南省资水流域汛期年均暴雨日数、暴雨量空间分布不均，上游地区年均暴雨日数（暴雨量）最小，其次为下游地区，中游地区最大；流域暴雨中心安化站年均暴雨日数最高为5.4 d，年均暴雨量最大为400.9 mm。

2）1980—2016年湖南省资水流域暴雨日数（暴雨量）时空变化整体上具有一致性：时间上，整体呈增加趋势（平均暴雨日数气候增长率为0.1 d/10 a，平均暴雨量气候增长率为13.1 mm/10 a），同时表现出明显的年际变化与突变特征，突变节点在1987年前后，此前为暴雨偏少期，此后为偏多期；空间上，偏多期时暴雨空间分布上具有正相关性，流域暴雨日数、暴雨量EOF分解以全局偏少模态出现年份最多（暴雨日数全局偏少9 a，暴雨量全局偏少15 a）。

3）汛期内流域暴雨日数上高度集中，平均暴雨集中度高达0.82，平均暴雨集中期为6月26日。流域中游暴雨集中度为0.83，暴雨集中期最早为6月21日。

4）汛期10 d 内流域大部分地区发生暴雨的概率低于20%，30d 内全流域暴雨发生的平均概率为32.2%。暴雨日数较多的地区暴雨以上降水发生的概率较高，暴雨日数较少的地区发生概率较低。