宽垄沟灌土壤水分累积入渗特性模拟研究

汪顺生，刘帅冶，傅渝亮*，王爱滨，陈春来，燕永芳

（1.华北水利水电大学 水利学院，郑州 450046；2.黄河水利科学研究院，郑州 450003）

0 引 言

【研究意义】宽垄沟灌技术属于沟灌的范畴，其水分入渗过程为二维入渗[1-3]。土壤体积质量、质地、灌水沟型、垄沟规格、土壤初始含水率、灌水时的压力水头等均会影响水分的入渗量[4-9]。目前，众多学者通过大量室内外试验对沟灌入渗的相关特性等方面开展了研究，但对宽垄沟灌的研究较少，缺乏较为系统的宽垄沟灌入渗模型。【研究进展】王庆杰等[10]对基于大垄宽窄行免耕种方式下的田间土壤结构、含水率和水分利用效率方面进行研究，探索了此模式在东北地区推广的可能性，但其对整个入渗过程中的入渗参数难以获取，且需要对大量田间实测数据进行筛选，应用受到一定限制；薛红利[11]研究了宽垄沟灌不同沟垄规格条件下水分运移过程，并得到了最佳垄沟规格。范严伟等[12]利用Hydrus-2D 对水平微润灌湿润体进行模拟，得到了较好的模拟值。张勇勇等[13]利用Hydrus-2D 软件对垄沟灌溉土壤水分的入渗过程进行了模拟，并且采用空间矩分析法对不同因素对湿润体的影响进行了分析，结果较为理想，其研究对象为传统沟灌技术，并未对宽垄沟灌进行相关研究。【切入点】综上所述，目前对入渗量和入渗模型的研究基本上是基于传统沟灌技术，对宽垄沟灌的入渗特性研究较少。【拟解决的关键问题】基于此，本文探究宽垄沟灌水分入渗特性及规律，采用数值模拟、理论分析与室内验证试验相结合的方法，对5种不同压力水头和土壤初始含水率条件下的宽垄沟灌进行试验。分析土壤初始含水率和压力水头对土壤水分入渗的影响并建立累积入渗量模型。

1 材料与方法

1.1 试验材料

试验于2019年1—5月在华北水利水电大学农业高效用水试验室进行（34°50′N、113°48′E，海拔110.4 m），属于河南省中部地区。试验区土壤为沙壤土，体积质量为1.35 g/cm3，田间持水率为24%（体积含水率），有机质量为0.87%。

1.2 试验方案

试验在室内模拟1/2 宽垄沟灌水分入渗过程。试验设备由土箱和马氏瓶供水系统组成。土箱由有机玻璃制作，长、宽、高分别为60、6、90 cm，土箱单侧每10 cm 开直径2 cm 小孔以便取样。在土箱底部开有微小排气孔防止气阻。由马氏瓶供水并保持沟中水深恒定至灌水结束。

试验用土取自0～30 cm 闲置的耕层土壤。对所取土样进行风干、碾压处理后过2.0 mm 筛。分别定量称取土样和去离子水，将所称土样分层均匀喷洒去离子水，并用薄膜覆盖静置24 h 后测量其含水率是否符合试验设计含水率。若符合则按平均体积质量1.35 g/cm3，将土样每10 cm 分层装入土箱，若不符合则重新配置。文中所指含水率均为体积含水率。

试验采用正交法，入渗时间为120 min，土壤体积质量为1.35 g/cm3，土壤初始含水率分别设置为8%、10%、12%、16%和20%，压力水头分别设置为3、6、9、12 cm 和15 cm，共25个水平组。每个试验组均设置3个重复，取其平均值进行分析。

1.3 观测项目和方法

1）累积入渗量：在试验过程中，每隔10 min 记录马氏瓶内水位读数，马氏瓶内消耗水量即为该时间段内的水分入渗量。

2）土壤含水率：当试验结束时，立即停止供水取出土样，并采用烘干法测定含水率。

1.4 土壤水分模拟参数

使用BT-9300ST 型激光粒度分布仪对供试土壤进行土壤颗粒组成测定，其颗粒组成和土壤质地如下：粒径小于1.000 mm的土壤颗粒占比为100%；粒径小于0.500 mm的土壤颗粒占比为98.49%；粒径小于0.125 mm的土壤颗粒占比为68.58%；粒径小于0.050 mm的土壤颗粒占比为45.93%；粒径小于0.025 mm的土壤颗粒占比为31.27%；粒径小于0.008 mm的土壤颗粒占比为14.71%。

土壤水动力参数根据土壤颗粒级配及土壤体积质量，应用Hydrus-2D 软件中Rosetta 模块预测土壤水分运动特征曲线（V-G模型）参数，即土壤残余含水率θr为0.032 cm3/cm3，饱和含水率θs为0.371 cm3/cm3，渗透系数Ks为2.718 cm/min，经验拟合参数α为0.017，n为1.459。其中土壤水动力参数α、n的确定需通过Hydrus-2D 将实测体积含水率作为输入项，通过迭代逆推参数值，利用最小二乘法原理使迭代后的参数值残差最小，即为参数值最优解[14]。

2 宽垄沟灌土壤水分入渗试验与模型建立

2.1 宽垄沟灌土壤水分入渗试验

试验设计土壤初始含水率为14%，压力水头为9 cm，按照上述试验方案进行水分入渗试验测量实际累积入渗量。并使用Hydrus-2D 软件对相同条件下的入渗过程进行模拟，所得模拟结果与实测结果较为接近，模拟效果较好（图1）。在土壤水分入渗前期，入渗速率较快且逐渐减小，累积入渗量呈非线性变化趋势。经过一段时间后入渗逐渐稳定，累积入渗量也随之达到线性稳定状态。

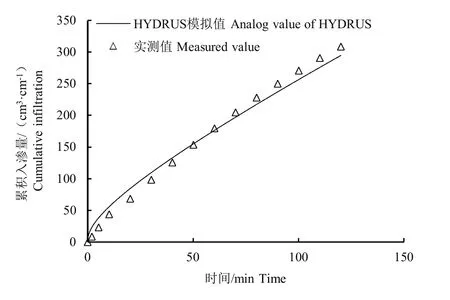
图1 累积入渗量实测值与模拟值比较Fig.1 Comparison of cumulative infiltration calculations with simulated values

2.2 宽垄沟灌土壤水分运动模型

2.2.1 土壤水分运动方程

1）宽垄沟灌水分入渗运动方程

宽垄沟灌为二维入渗，采用Hydrus-2D模拟土壤水分入渗，假设土壤为均质土并且具有各向同性，不考虑土壤内部的空气、温度以及蒸发等因素对入渗的影响，沟灌二维入渗的土壤水分运动方程采用Richards 方程进行求解，详见参考文献[15]。

2）边界条件：

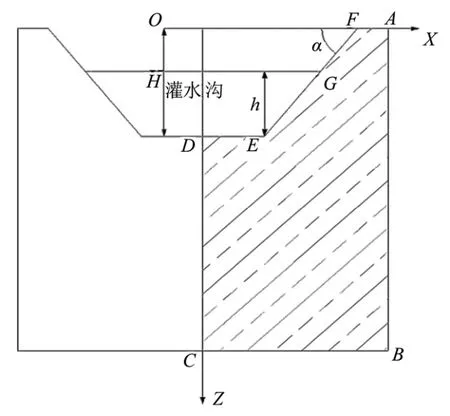
图2 沟灌模型Fig.2 Physical model of furrow

宽垄沟灌的灌水沟断面呈对称梯形（图2），在试验和模拟中仅考虑阴影区域即ABCDEF 区域内的水分运动。GF、FA 始终覆盖塑料薄膜，可忽略水分蒸发，因此视为大气边界，左右边界DC、AB的水平通量为0，视为0 通量面，BC 边界设置了排水孔，在试验过程中湿润锋未达到此处，未对土壤水分入渗产生影响，故设为自由排水边界[13]。灌水沟深度为H，在模拟水流入渗过程中，DE 和EG 边界随时间的推移发生变化，沟中水深即压力水头h，沟中DE 和EG面在灌水过程中总水势为h-H；在本次模拟中入渗时间为120 min，边界条件定解方程可表示为：

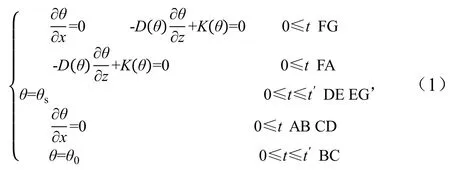
式中：θ为土壤含水率（cm3/cm3）；θ0为初始含水率（cm3/cm3）；D（θ）为土壤水分扩散率（cm2/min）；t΄为入渗结束时刻。

2.2.2 累积入渗量计算模型

根据2.1 中试验所得水分入渗特性并参考傅渝亮等[14]的研究，宽垄沟灌土壤水分累积入渗过程与电容充电过程较为类似。水分累积入渗量随时间变化模型的建立可参考电容充电模型。假设在此时间段内2个入渗过程存在明显的分界点，在非线性入渗阶段累积入渗量为Q1，由电容充电模型可得其随时间变化的函数关系表示为：

式中：Q1为非线性阶段累积入渗量（cm3/cm）；a为体积常数，表示在非线性入渗阶段水分入渗的极限值；b为时间常数，表示水分入渗由非线性入渗到线性入渗所用的时间。

在稳定入渗阶段，累积入渗量随时间变化的函数关系可表示为：

式中：Q2为稳定入渗阶段累积入渗量（cm3/cm）；c为稳定入渗阶段的土壤水分入渗速率（cm3/（cm·min））。

整理可得在模拟时间内的整个入渗过程的累积入渗量Q为：

2.3 初始含水率对累积入渗量的影响

使用Hydrus-2D 软件对压力水头为12 cm，不同初始含水率下的供试土壤进行120 min 宽垄沟灌模拟入渗试验。对5种不同初始含水率下的累积入渗量模拟结果进行比较（图3），初始含水率为10%、12%、16%和20%条件下的累积入渗量较初始含水率为8%条件下的模拟结果分别减少了2.15%、4.34%、8.89%和13.72%，随着初始含水率的增大，累积入渗量逐渐下降。入渗是土壤空隙逐渐被水分占据的过程，空隙越强，则水吸力越强，对水分进入土壤空隙越有利。因此，当土壤初始含水率处在较小的水平时，土壤基质势较大，水分进入土壤相对容易，水分累积入渗量越多。当土壤初始含水率增大时，土壤含水率逐渐向饱和状态靠近，累积入渗量也随之减小。

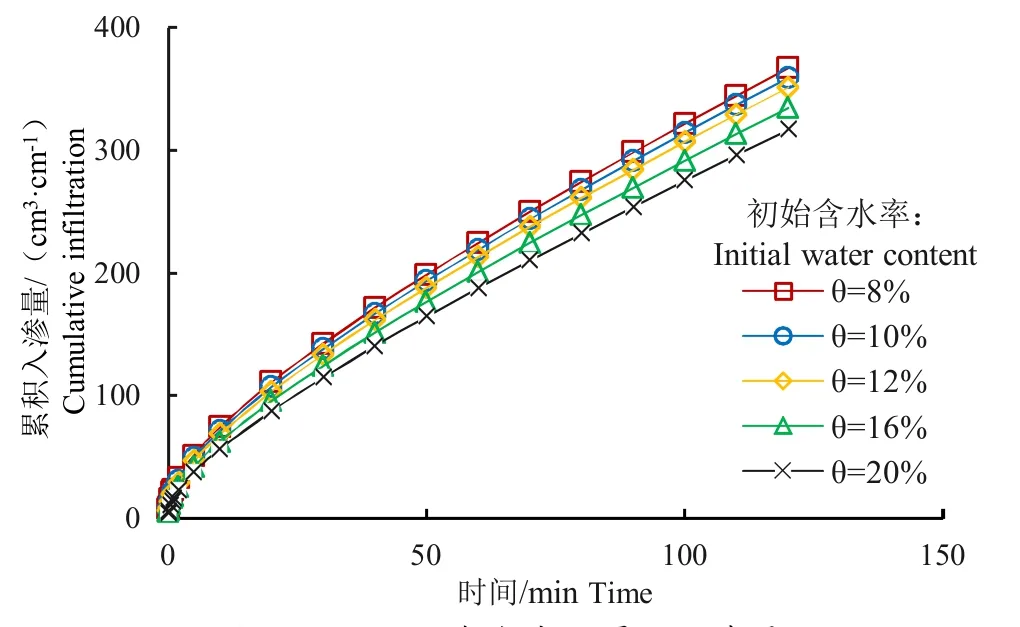
图3 不同初始含水率下累积入渗量Fig.3 Cumulative infiltration under different initial water content

根据Hydrus-2D 软件模拟宽垄沟灌水分入渗的结果，利用MATLAB 软件对模拟结果与式（4）累积入渗量模型进行拟合，分别计算出在相同压力水头时，得到初始含水率与累积入渗量模型系数的关系。

1）采用线性进行拟合可得系数a在不同压力水头下与初始含水率的关系为：

系数a与初始含水率的拟合度均在0.96 以上，且存在线性关系，即随着初始含水率的增大，非线性入渗阶段的累积入渗量随之减小，这与整个入渗阶段的累积入渗量变化趋势一致。

2）采用线性进行拟合可得系数b在不同压力水头下与初始含水率的关系为：

系数b与初始含水率的拟合度均在0.94 以上，并发现系数b随初始含水率的增大而增大，即随着初始含水率的增大，非线性入渗阶段的过程也越长。

3）采用线性进行拟合可得系数c在不同压力水头下与初始含水率的关系为：

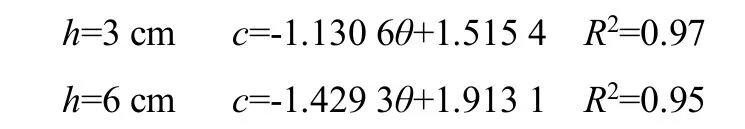
系数c与初始含水率的拟合度均在0.93 以上。系数c与初始含水率存在线性减小关系，从土壤特性角度分析，初始含水率的增大，使土壤水吸力减小，减小土壤水入渗能力，从而使得稳定入渗阶段水分入渗速率下降。

由以上分析发现，模型系数a、b随初始含水率的增加而增大，而模型系数c则随之减小。说明初始含水率的增大可使非线性入渗时间增长。初始含水率对模型系数a、b的影响较大，对模型系数c的影响较小，由此可知，初始含水率对水分入渗的非线性阶段较为明显，增大初始含水率可使非线性阶段的入渗量增加，对线性阶段的入渗量影响不明显。

2.4 压力水头对累积入渗量的影响

使用Hydrus-2D 软件对初始含水率为16%，不同压力水头下的供试土壤进行宽垄沟灌模拟入渗试验，累积入渗量随时间变化情况见图4。由图4所知，灌水压力水头越大，累积入渗量越大；在入渗初期入渗速率最大但逐渐减小，最后达到相对稳定入渗水平。

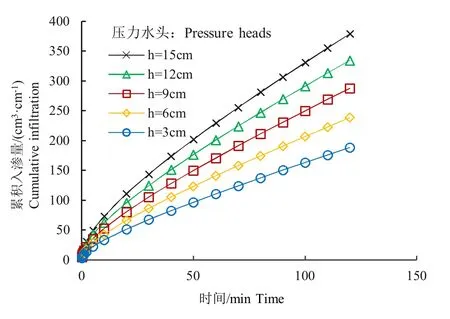
图4 初始含水率为16%时不同压力水头下累积入渗量变化Fig.4 θ=16%,Cumulative infiltration change under different pressure heads

相同条件下，压力水头为6、9、12 cm 和15 cm时的累积入渗量较压力水头为3 cm 分别增加了26.77%、52.81%、77.83%和101.49%。由此可知，压力水头对累积入渗量影响较大，压力水头的增大，累积入渗量逐渐增大，但是随着压力水头的增大，累积入渗量的增加幅度逐渐减小。从土壤水分入渗特性分析可知，在其他条件相同的情况下，灌水时压力水头越大，入渗湿周增大，水分与土壤的接触面积更大，因此在模拟结束时累积入渗量相应的增加。

根据宽垄沟灌水分入渗模拟的结果，利用MATLAB 软件对不同压力水头下的模拟结果与式（5）土壤水分累积入渗量进行拟合，计算出在同一初始含水率下压力水头与模型系数的关系。

对模型系数a与压力水头进行线性拟合得出：

模型系数a与压力水头拟合度均在0.95 以上，且存在明显线性关系。主要原因为随着压力水头的增大，水分与沟中土壤的接触面积增大，相应的接触面土壤的孔隙总体积增大，非线性入渗阶段累积入渗量增大，因此模型系数a随着压力水头的增大而增大。

对模型系数b与压力水头进行线性拟合得出：

系数b与压力水头的拟合度在0.92 以上，且存在线性关系。模型系数b随压力水头的增大而增大，即达到稳定入渗的时间增大。其原因是由于土壤水分入渗速率主要受土壤吸力影响，与压力水头关系不大。当压力水头增大使非线性入渗量增大，从而导致非线性入渗时间的增大。

对模型系数c与压力水头进行线性拟合得出：

系数c与压力水头的拟合度在0.96 以上，且存在线性关系。其原因为在稳定入渗阶段，压力水头的增大，土水接触面土壤均达到了饱和状态，此时土壤水分入渗由于压力水头的增大，水压力变大，对土壤水分入渗有促进作用，因此稳定阶段水分入渗速率增大，即模型系数c随压力水头的增大而增大。

由以上分析可知，压力水头的增大可使模型系数a、b、c增大，即压力水头影响了入渗的全过程。但对系数a和b影响较为明显，说明压力水头对累积入渗量的影响主要是在非线性入渗阶段，对线性入渗阶段影响较小。其原因为稳定入渗阶段的入渗速率由土壤吸力决定，受其他因素影响不大。

3 模型分析与验证

3.1 累积入渗量模型

根据Hydrus-2D模拟计算所得不同压力水头和初始含水率下的累积入渗量模型系数。对各参数进行方差分析，结果见表1。

压力水头和土壤初始含水率分别对累积入渗量模型系数的影响极显著（p＜0.01），这与上文分析结果基本一致，而压力水头和初始含水率交互作用下对模型系数的影响不显著（p＞0.05）。

通过MATLAB 拟合结果，建立宽垄沟灌土壤水分累积入渗量模型系数a、b、c分别与压力水头和初始含水率的综合关系：

其拟合度均在0.96 以上，且土壤初始含水率与模型系数a和c存在负相关关系，与系数b存在正相关关系，而压力水头与3个系数均存在正相关关系。因此宽垄沟灌土壤水分累积入渗量模型可以表示为：

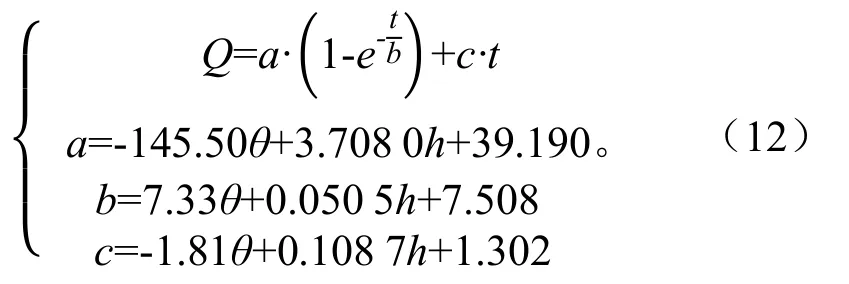
图5 累积入渗量计算值与模拟值比较Fig.5 Comparison of cumulative infiltration calculations with simulated values

3.2 模型验证

为了进一步验证累积入渗量模型的准确性，在室内土箱中进行宽垄沟灌水分入渗试验。试验设计土壤初始含水率为9.3%，压力水头为9 cm。试验实测累积入渗量与所建累积入渗量模型计算值拟合结果见图5。通过实测值与模拟值相比较发现，实测值与模拟值间误差较小，模拟效果较好。

4 讨 论

本文运用Hydrus 软件分别模拟了在不同初始含水率和不同压力水头条件下的宽垄沟灌入渗量。试验开始前，将累积入渗量实测值与Hydrus-2D模拟值进行拟合，验证Hydrus-2D 数值模拟中水分参数的可靠性，其拟合程度均在较高水平，说明模拟参数的选取合理，可以在本研究中作为试验的辅助手段。这与范严伟等[12]、张勇勇等[13]研究结果一致。宽垄沟灌土壤水分累积入渗量随时间的变化参考电容充电模型[14]进行分析，逐步建立累积入渗量模型。

试验结果发现，随着初始含水率的增加，累积入渗量逐渐减小；累积入渗量随压力水头的增大而增大，但增幅减小。由于土壤水入渗过程是水填充土颗粒之间孔隙并挤压其中气体的过程，入渗初始阶段入渗速度较快，并逐渐达到稳定，这与土壤基质势逐渐减小有关。

利用MATLAB 软件进行拟合得宽垄沟灌累积入渗量模型并发现，土壤初始含水率对模型系数a、c存在负相关关系，与模型系数b存在正相关关系，分析原因为：系数a与初始含水率有明显的线性减小关系，说明随着初始含水率的增大，非线性入渗阶段的累积入渗量也随之减小；系数b与土壤水分初始含水率存在线性增加关系，非线性入渗阶段与线性入渗阶段的时间分界点随着土壤初始含水率的增加而延后；系数c与初始含水率存在线性减小关系，从土壤特性分析考虑，初始含水率的增大，使土壤水吸力减小，对水分入渗的作用减小，从而使得稳定入渗阶段水分入渗速率下降。此部分结果与前人研究[16-18]结果一致。压力水头与宽垄沟灌累积入渗量模型系数a、b、c存在正相关关系，即压力水头的增长促进了水分的入渗，原因如下：随着压力水头的增大，水分与沟中土壤的接触面积增大，相应的接触面土壤的孔隙总体积增大，非线性入渗阶段累积入渗量增大；系数b由于压力水头的增大而增大，是因为水分与土壤接触面增大，非线性入渗阶段水分进入土壤的累积入渗量增大；系数c与压力水头存在明显的线性增大关系，原因可能为，在稳定入渗阶段，压力水头的增大，土水接触面土壤均达到了饱和状态，此时土壤水分入渗由于压力水头的增大，水压力变大，对土壤水分入渗有促进作用。此部分结果与前人研究结果[19-21]一致。

5 结 论

随着土壤初始含水率和压力水头的增大，累积入渗量分别表现出减小和增大的趋势；初始含水率和压力水头对模型系数的影响极显著（p＜0.01），而在二者交互作用下对模型系数的影响不显著（p＞0.01），且二者对入渗过程的影响主要集中在非线性阶段，对稳定入渗阶段的作用并不明显。