一种次优PTS-WHT 联合峰均比抑制算法

孙乾乾，陈斌杰，赵健博

1. 哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001 2. 北京遥感设备研究所，北京 100854

正交频分复用技术凭借抗多径效应的能力强、频谱利用高、易于其他多种接入方法相结合等特性在许多领域中得到应用，如3GPP 的长期演进(long term evolution，LTE)标准，以及即将推出的5G 通信系统。OFDM 系统的主要缺点之一是信号峰值功率与平均功率的比值偏高[1]。目前提出的降低OFDM 系统的PAPR 的方法共分为3 类:信号预畸变方法、编码类方法、概率类方法。其中，信号预畸变方法会导致信号失真[2-3]，编码方法适用于子载波数目较少的系统，在子载波数目过多时其算法复杂度过高，所以概率类技术成为降低PAPR 的主要方法。现有的概率类技术包括选择性映射算法(selected mapping，SLM)[4-5]、部分传输序列算法[6]等。

本文将针对PTS 和WHT 进行研究，提出一种联合算法提高PAPR 抑制性能，同时不过多增加算法的计算量，达到算法复杂度和算法性能的折中。

1 OFDM 系统及峰值均值功率比

OFDM 系统是一种多载波数字调制方案。其信号是由调制后的多个子载波叠加而成的。假设OFDM 系统有N个子载波，其周期为T，每个子载波承载的数据为Aj(i=0,1,···,N-1)，第0 个子载波频率为fc，第i个子载波的频率为则OFDM符号可以表示为

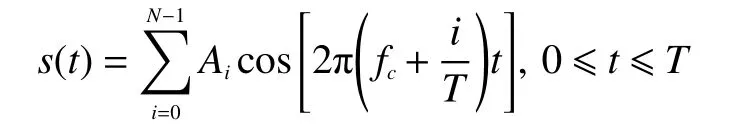
通常采用快速傅里叶变换(fast Fourier transform，FFT)来实现OFDM 的调制。设Xk表示OFDM的频域信号，经过IFFT 变换后得到时域信号xn，其中xn与Xk的关系如下

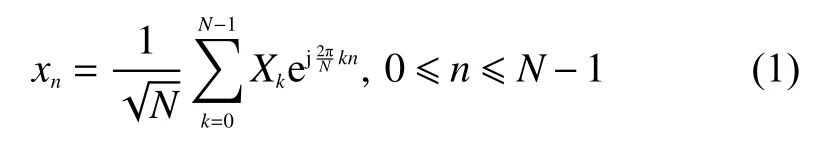
信号峰值功率与均值功率的比值称为峰值均值功率比简称峰均比，这里PAPR 的值可用公式表示为[7]

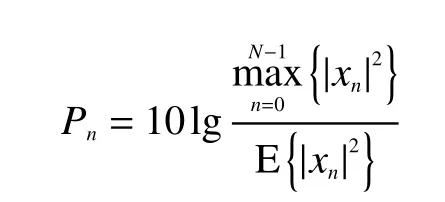
由峰均比定义可知OFDM 子载波的同相叠加是一个随机过程。为了直观地表述OFDM 信号的峰均比，可以使用互补累计分布函数(complementary cumulative distribution function，CCDF)在统计学的角度上表示信号的PAPR。互补累计分布函数表示OFDM 信号的PAPR 大于所设定的PAPR 值门限z的概率[8]:

2 部分传输序列算法

部分传输序列算法是降低OFDM 信号PAPR的一种常用方法，PTS 算法的基本原理是将原始序列分割成V个不同的子块，每个子块分别乘以不同的相位旋转因子后进行相加合并，通过改变各个子块所乘的相位旋转因子使PAPR 尽可能小。PTS 的原理框图如图1 所示。

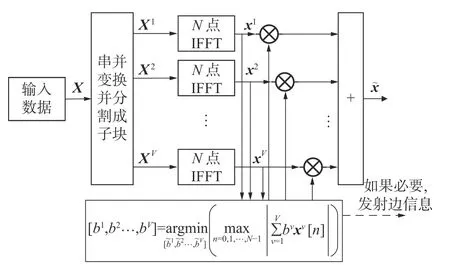
图1 PTS 原理框图

输入的OFDM 原始信号X=[X0,X1,···,XN-1]首先被分割为V个子块，对每一个子块进行相位加权并合并，得到

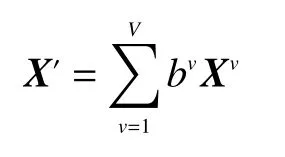
式中bv=ejφv为相位加权因子，称为边带信息，其中v=1,2,···,V为子块序号。经过N点IFFT 后得到时域OFDM 符号:

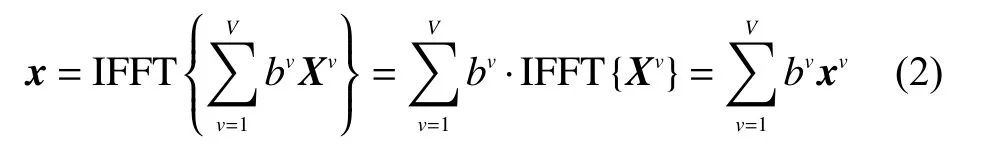
式中bv的选择应满足:

从式(2)来看，bv的值可以在[0,2π)之间任取，以得到PAPR 抑制的最佳性能。但当集合中包含的相位加权因子U很大时，bv共有UV种可能取值，每个符号需要VUV次IFFT 才能最终确定加权系数，这样的计算量过于巨大，不适合实际OFDM通信系统中的应用。因此需要将bv限制在合适的取值范围内，文献[9]提出了一种次优PTS 算法，该算法使用一种二进制相位因子{1,-1}，以降低系统的计算复杂度。

次优PTS 算法的峰均比抑制性能与分块数相关，分块数越多次优PTS 算法的峰均比抑制性能越好。次优PTS 算法的性能与分块数的关系如图2 所示。

图2 不同子块数PTS 算法峰均比抑制性能

3 沃尔什哈达玛变换

沃尔什哈达玛变换(WHT)是沃尔什(Walsh)变换和哈达玛(Hadamard)变换的统称，WHT 的构成十分简单，是一个只由1 和-1 组成的有序序列[10]。WHT 只需要进行简单的加减运算就可以得到，不需要进行大量的复数乘法运算，这样使得WHT具有较低的运算量。

WHT 是以Walsh 函数为基本函数的一种正交变换。Walsh 函数由拉德梅克(Rademacher)函数得到，拉德梅克函数R(n,t)的定义为[11-13]

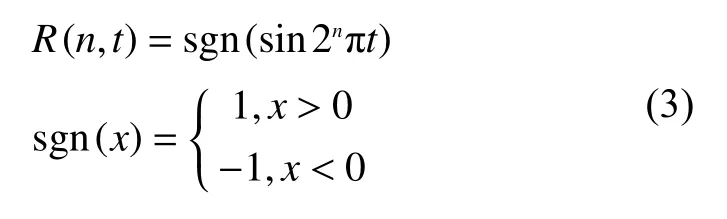
从式(3)可以看出拉德梅克函数是一个由1 和-1 组成的周期函数。Hadamard 排列的walsh变换如下

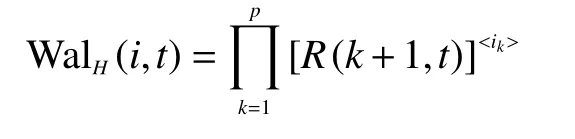
式中:R(k+1,t)是拉德梅克函数，是倒序的二进制码的第k位，k=1,2, ···,p。一维WHT 及其逆变换的定义为

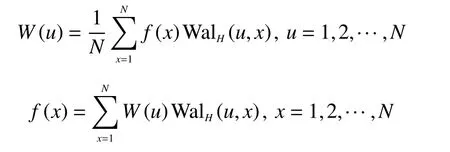
Walsh-Hadamard 矩阵是正交矩阵的一种，可以通过递推的方法生成。以N阶Walsh-Hadamard矩阵为例，其生成方式如下:

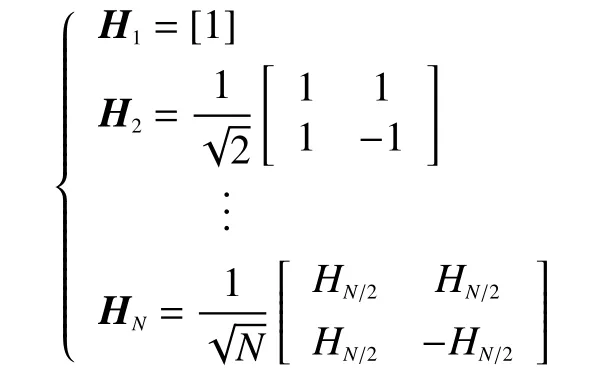
式中矩阵前的系数为归一化系数。

根据式(1)中所假设的信号，离散时间信号的功率可由式(4)得出:

其中:

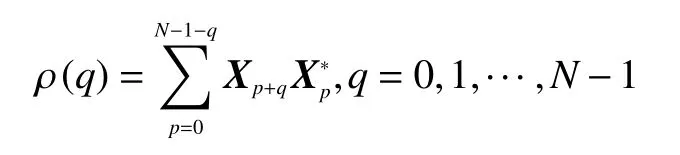
是序列X的非周期自相关函数序列S。

假设OFDM 信号xn的平均功率为1，则该信号的PAPR 的最大值为

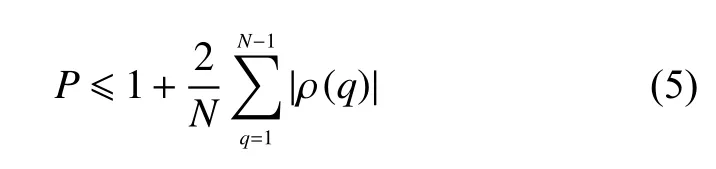
由式(5)可知，一个信号的PAPR 值和该信号的自相关函数值有关。并且自相关函数值越小，该信号的PAPR 越小。

假设S为矩阵H与输入序列X相乘得到的序列， ρS、 ρX分别为序列S和序列X的自相关函数。我们可以得到

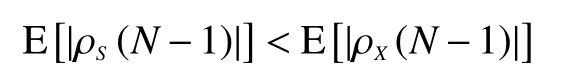
根据式(5)可得

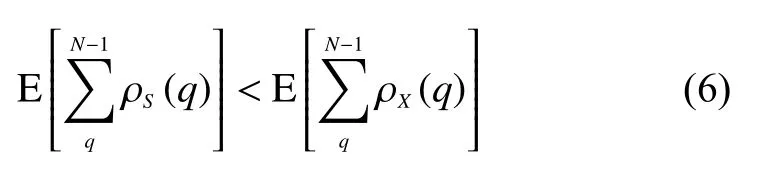
由式(6)可得，经过WHT 后信号的自相关函数的均值减小了，进而推断出进行变换后的序列的PAPR 减小。

4 次优PTS-WHT 联合算法

联合算法的主要思想是先对数据进行低峰均比值的WHT，再利用PTS 算法进一步优化。PTS算法使用搜索次数低的次优算法，从而达到复杂度低、性能好的效果。

4.1 次优PTS-WHT 联合算法

图3 为次优PTS-WHT 联合算法框图。

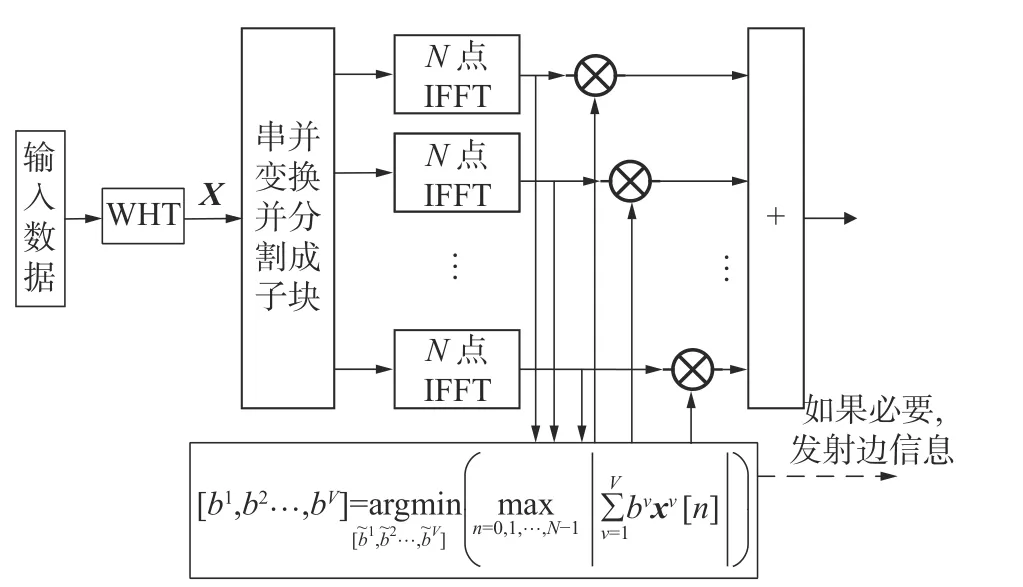
图3 次优PTS-WHT 编码算法框图

该方法的主要步骤如下:

1)将输入的OFDM 的串行数据进行串并变换，并进行数字映射，得到N个已映射的数据；

2)生成一个N×N的WHT 矩阵，并与输入数据相乘，生成已编码的数据；

3)采用相邻分割的方式将输入OFDM 信号分成V个子块；

4)对V的子块数据进行IFFT 变换；

5)设置所有的相位因子bv=1，进行运算之后得到信号的PAPR 值，将其设为Pmin；

6)设置v=2，在bv=-1的情况下，找到其中的PAPR；

7)如果PAPR 值大于Pmin，那么bv=1；否则，更新PAPR 值为Pmin；

8)如果v＜V，那么v加1，然后回到步骤7)，否则得到最优的相位因子b˜；

9)将得到的最优相位因子b˜与傅里叶变换之后的数据相乘，作为最优的序列发送。

4.2 联合算法仿真分析

对次优PTS-WHT 联合算法进行Matlab 仿真分析。本次仿真实验的基本参数设置如下:OFDM符号数为3 000，调制方式为QPSK，子载波数为256，IFFT 取256 点，CP 长度为36，实验中可选择的相位因子为b=[1,-1]，子块数目为4 块，次优PTS 算法采用随机交织。图4 为OFDM 原始信号通过次优PTS-WHT 联合算法和次优PTS 算法的CCDF 分布图。图中可以看出相比于次优PTS算法，本文提出的联合算法的PAPR 值降低了0.5 dB 左 右，OFDM 系统的PAPR 得到了较大的优化。

图4 PAPR 的CCDF 分布

改变次优PTS 算法的子块数为8，次优PTSWHT 算法子块数不变，其余仿真参数同上。图5为OFDM 原始信号、分块数为8 的次优PTS 算法和分块数为4 的次优PTS-WHT 联合算法CCDF分布图。

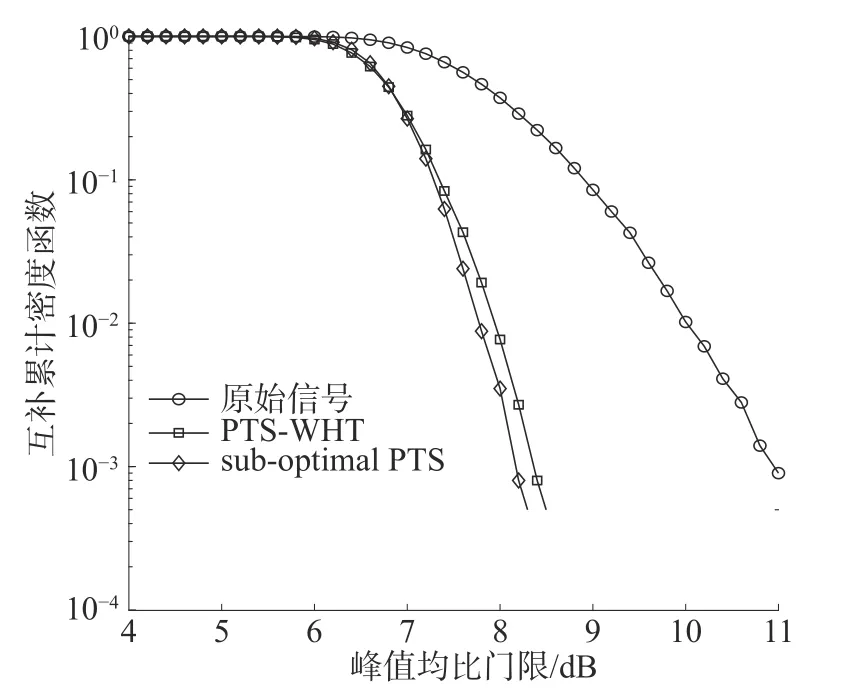
图5 8 子块PTS 与PTS-WHT 的CCDF 分布

从图5 中可以看出，在次优PTS 算法分块数增加一倍时，其峰均比抑制性能与次优PTS-WHT联合算法相近。但是此时的次优PTS 算法增加了1 024 次IFFT 运算，而次优PTS-WHT 联合算法仅仅增加了1 024 次乘法运算。由此可见在PAPR抑制性能近似时，次优PTS-WHT 算法运算量远远低于次优PTS 算法。

5 结论

本文提出了一种基于次优PTS-WHT 联合算法，并对现有的次优PTS 算法进行了仿真并进行对比。仿真结果表明:

1)在分块数相同的的情况下，联合算法的PAPR 抑制性能相比次优PTS 算法提升了0.6 dB。

2)在实现相同的PAPR 抑制性能的条件下，次优PTS-WHT 联合算法运算量则远低于次优PTS 算法。

因此联合算法可以在不过多增加运算量的条件下实现良好的PAPR 抑制效果。