不同长度耗能梁段偏心支撑框架受力性能

孙山川，王新武，孙海粟，时 强

(1.河南科技大学 土木工程学院，河南 洛阳 471023；2.洛阳理工学院 土木工程学院，河南 洛阳 471023)

0 引言

偏心支撑钢框架是近些年来发展起来的一种抗震结构形式，其特点是支撑斜杆两端中至少有一端是不在梁柱节点处相交的，这样柱与斜杆之间，或者斜杆与斜杆之间会形成一个耗能梁段[1-2]。偏心支撑结构体系具有中心支撑的特点[3]，能够提供较高的强度和刚度。在强地震作用下，通过耗能梁段的非弹性变形进行耗能，使耗能梁段的剪切屈服在先，从而保护支撑斜杆不屈服或屈服在后[4-7]。因此，具有耗能梁段的偏心支撑钢框架兼顾了纯抗弯钢框架和中心支撑钢框架的优点。目前，国内外多采用有限元的方法分析不同结构形式偏心支撑钢框架的受力性能，如文献[8-10]用有限元软件ABAQUS，研究了梁柱线刚度比、耗能梁段长度和轴压比变化等对偏心支撑钢框架抗震性能的影响。采用有限元软件降低了研究的成本，具有一定的优势，但缺乏考虑实际存在的施工误差等因素。本文将通过试验研究不同长度耗能梁钢框架的受力情况，根据直接采集到的真实数据分析耗能梁段长度对框架性能的影响[11-14]。

1 试验

1.1 试件设计

在保证柱间梁段和耗能梁段总长度不变的情况下，通过调整耗能梁段长度和梁段长度得到3种K型偏心支撑钢框架结构。耗能梁段长度分别为400 mm、600 mm和800 mm的K型偏心支撑钢框架模型图见图1，试件名称分别为EBF-1、EBF-2和EBF-3。

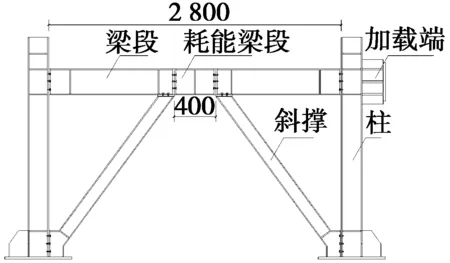
(a) EBF-1(耗能梁段长度400 mm)

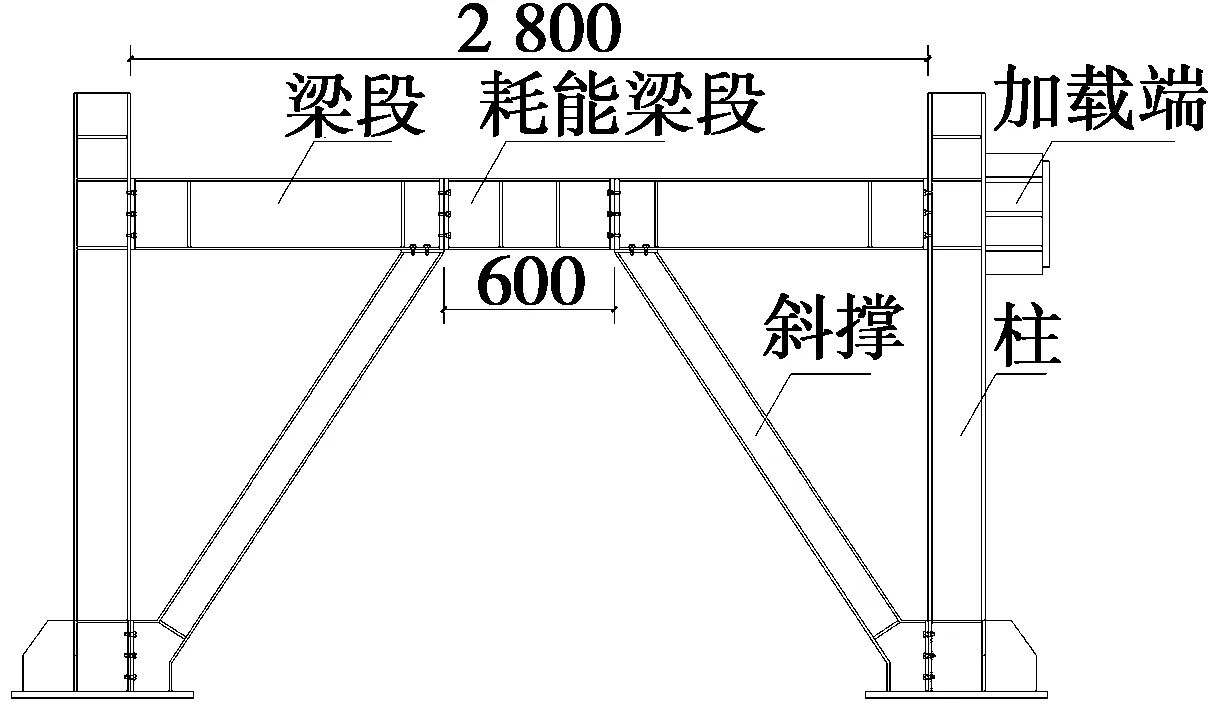
(b) EBF-2(耗能梁段长度600 mm)

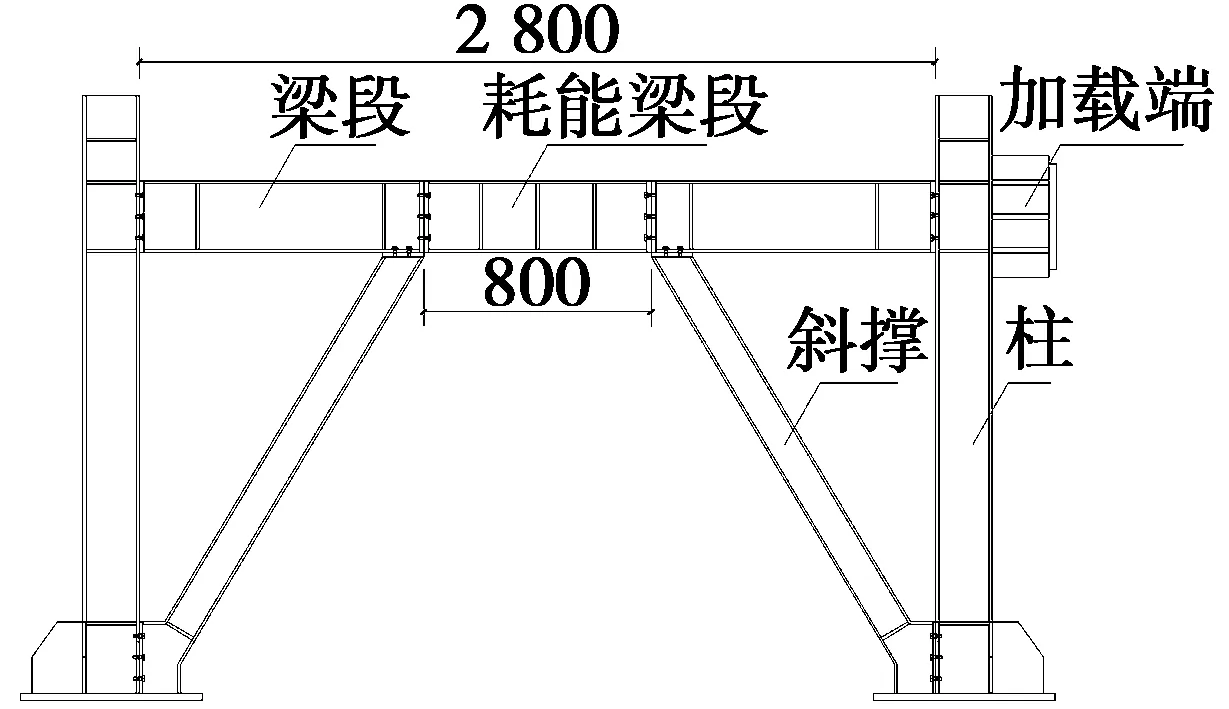
(c) EBF-3(耗能梁段长度800 mm)

图1 K型偏心支撑钢框架模型图

表1为偏心支撑钢框架主要构件参数。偏心支撑钢框架中，梁与柱、梁与耗能梁、梁与斜撑、斜撑与柱均通过高强螺栓摩擦型连接，螺栓的型号均为M20。

表1 偏心支撑钢框架主要构件参数

注：HW指H型钢高度和翼缘宽度基本相等；HN指H型钢高度和翼缘宽度比例≥2。

1.2 材料属性

在同一批次的钢材中取试件进行单向拉伸试验，测定的主要材料属性为弹性模量E、屈服强度Rp0.2、极限抗拉强度Rm和断后伸长率A。材料属性试验所需的样胚严格按照GB/T 2975—1998《钢及钢产品 力学性能试验取样位置及试样制备》[15]要求制作,根据 GB/T 228.1—2010《金属材料 拉伸试验 第1部分：室温试验方法》[16]确定材料属性试验所需试件的形状尺寸和具体的试验方法,试验得出的试件材料属性如表2所示。

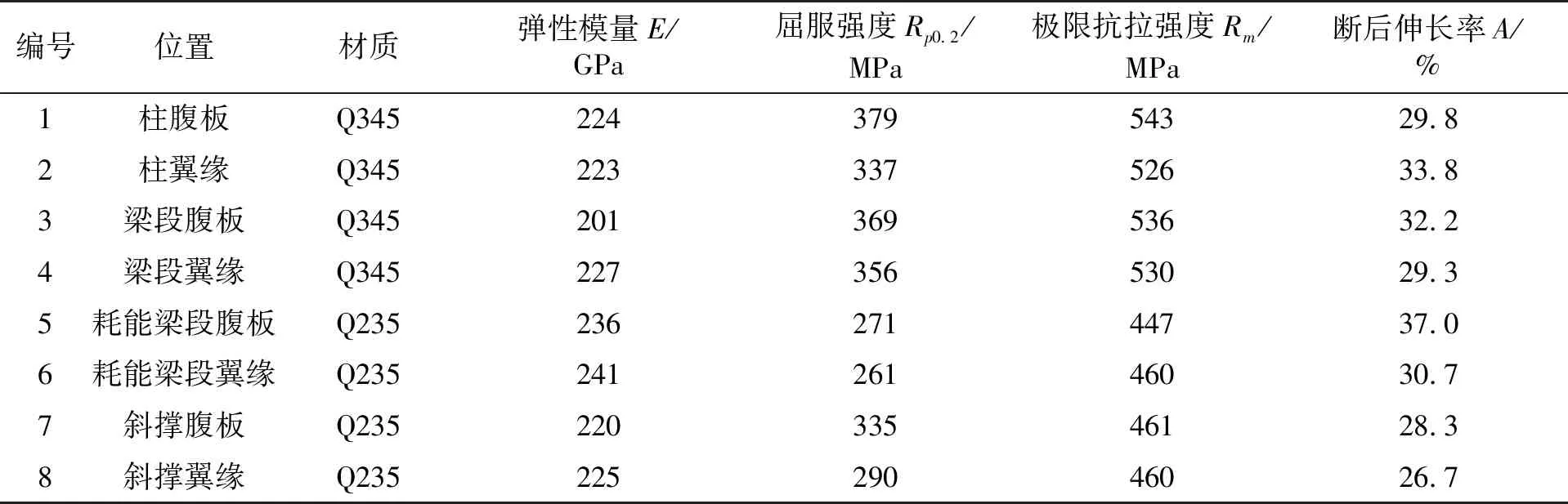
表2 试件材料属性

1.3 试验加载

偏心支撑钢框架拟静力试验采用梁端加载，试件结构加载示意图如图2所示。试验开始前对偏心支撑钢框架进行预加载，保证装置的正常运行。试验中，同时在偏心支撑钢框架两个柱子顶端加载200 kN的轴向压力，整个试验过程中保持轴向压力不变。

图2 试件结构加载示意图

循环加载制度采用荷载-位移混合控制法，见表3。正式试验时，先对柱顶施加预定的轴向压力，待框架达到稳定后，采用荷载控制对偏心支撑框架施加水平荷载，逐步增加荷载直至构件达到屈服应变，进而得到屈服位移。以屈服位移为基础逐级增加，进行低周循环往复加载试验，直至构件破坏时终止试验。

表3 循环加载制度

注：△y为屈服位移,mm；εy为屈服应变；×3代表循环3次。

1.4 监测方案

框架左右两端对应梁截面形心处各放置1个量程为-150～150 mm的水平针状位移计，以此测量框架的整体水平位移。耗能梁段上翼缘左右两边各放置1个量程为 -50～50 mm的竖直针状位移计，以此测量耗能梁段左右两边竖直方向的上下错位位移差。梁与斜撑、斜撑与柱以及柱与梁等连接处各放置1个拉线位移计，以此测量整个试验过程中构件之间的转角与荷载变化的关系。

2 试验结果和分析

2.1 循环加载

荷载控制阶段，构件均处于弹性阶段，没有明显的变形。位移控制阶段，随着位移的增加，耗能梁段变形越来越明显。耗能梁段腹板剪切变形较大，整体倾斜明显。直到试验结束时，左右两边的柱子、斜撑与梁组成的三角形结构保持稳定状态。

2.1.1 EBF-1试验

经试验测得当水平荷载达到247 kN时，耗能梁段腹板率先达到屈服应变，屈服位移△y为3.81 mm。EBF-1试验现象见图3。刚进入屈服阶段时，由于塑性变形较小，耗能梁段产生小的屈曲变形现象，耗能梁段与两端框架梁段之间出现缝隙，最大缝隙宽为5 mm，如图3a所示。经过强化阶段大的塑性变形，耗能梁段与两端框架梁段之间的缝隙进一步加大，最大缝隙达到10 mm，如图3b所示。当施加的水平荷载达到偏心支撑钢框架所能承受的极限承载力以上时，位移的加大加快了耗能梁段的弯曲变形，直至最后耗能梁段腹板撕裂破坏，如图3c所示，试验终止。

(a) 4△y时构件之间的缝隙

(b) 7△y时构件之间的缝隙

(c) 9△y时耗能梁段腹板撕裂破坏

图3 EBF-1试验现象

2.1.2 EBF-2试验

经试验测得当水平荷载达到189 kN时,耗能梁段腹板率先达到屈服应变，屈服位移△y为2.89 mm。EBF-2试验现象见图4。进入屈服阶段时，由于塑性变形较小，耗能梁段产生小的屈曲变形现象，耗能梁段与两端框架梁段之间出现缝隙，最大缝隙宽为6 mm，如图4a所示。经过强化阶段较大的塑性变形，耗能梁段与两端框架梁段之间的缝隙进一步加大，最大缝隙达到13 mm，如图4b所示。当施加的水平荷载达到偏心支撑钢框架所能承受的极限承载力以上时，位移的加大加快了耗能梁段的弯曲变形，直至最后耗能梁段腹板撕裂破坏，如图4c所示，试验结束。

(a) 6△y时构件之间的缝隙

(b) 8△y时构件之间的缝隙

(c) 10△y时耗能梁段腹板撕裂破坏

图4 EBF-2试验现象

2.1.3 EBF-3试验

经试验测得当水平荷载达到154 kN时,耗能梁段腹板率先达到屈服应变，屈服位移△y为3.67 mm。EBF-3试验现象见图5。构件进入屈服阶段时，由于塑性变形较小，耗能梁段产生小的屈曲变形现象，耗能梁段与两端框架梁段之间出现缝隙，最大缝隙宽为9 mm，如图5a所示。经过强化阶段较大的塑性变形，耗能梁段与两端框架梁段之间的缝隙进一步加大，出现耗能梁段与框架梁段相互挤压错动的现象，如图5b所示。当施加的水平荷载达到偏心支撑钢框架所能承受的极限承载力以上时，位移的加大加快了耗能梁段的弯曲变形，直至最后耗能梁段腹板撕裂破坏，如图5c所示，试验终止。

(a) 5△y时构件之间的缝隙

(b) 8△y时构件之间的挤压错动

(c) 10△y时耗能梁段腹板撕裂破坏

图5 EBF-3试验现象

2.1.4 循环加载对比分析

循环加载试验结果见表4。由表4可知：随着耗能梁段长度增加，屈服荷载降低，EBF-2的屈服荷载较EBF-1的降低23.50%，EBF-3的屈服荷载较EBF-1的降低37.55%；极限承载力降低，EBF-2的极限承载力较EBF-1的降低7.94%，EBF-3的极限承载力较EBF-1的降低19.65%。耗能梁段长度的增加，影响耗能梁段的屈曲形式和内力分布，耗能梁段长度对结构构件承载能力产生较大影响，偏心支撑钢架结构的极限承载力与耗能梁段破坏时的结构承载力均随耗能梁长度的增加呈下降趋势。

表4 循环加载试验结果

2.2 滞回曲线

图6为偏心支撑钢框架EBF-1试验所得的滞回曲线。由图6可以看出：由于构件之间缝隙的存在以及受力时螺栓孔的挤压变形，滞回曲线受到了滑移的影响，具有“捏缩”效应。因为构件与构件之间采用的是同一种连接方式(螺栓连接)，EBF-2、EBF-3所得的滞回曲线均与EBF-1滞回曲线相似，呈狭长状，同样具有“捏缩”效应，滞回曲线反映出整个偏心支撑钢框架结构较强的塑性变形能力。荷载控制阶段，试件处于弹性工作状态，表现出很好的线性关系。位移控制阶段，随着耗能梁段进入塑性变形阶段，位移和承载力的增大使滞回曲线不再呈线性显示，当水平荷载达到偏心支撑钢框架极限承载力时，位移的继续增大加快了耗能梁段的弯曲变形和最终破坏，反而使整体结构的承载能力下降，滞回曲

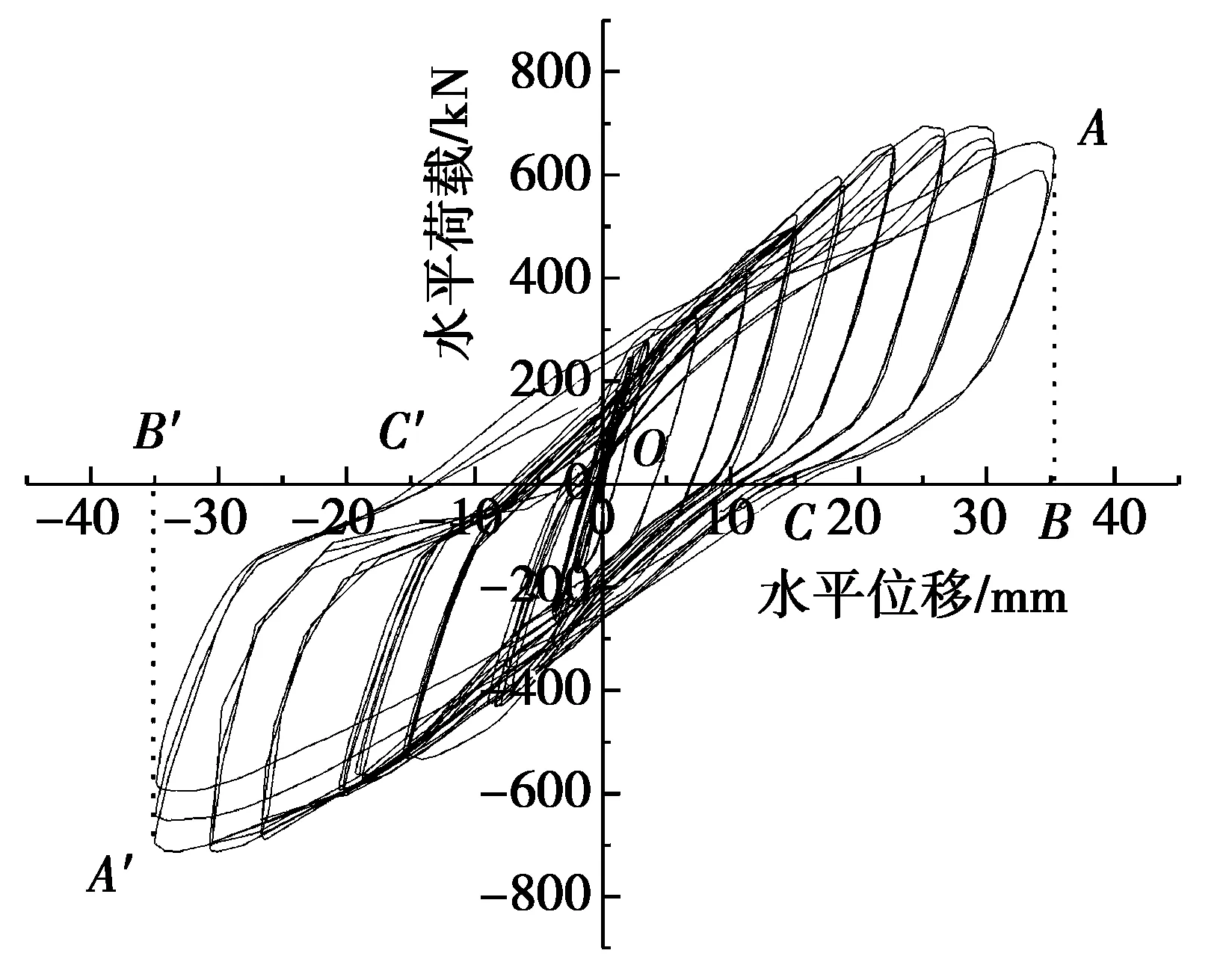
图6 EBF-1滞回曲线

线呈现出下降的趋势，直至耗能梁段撕裂破坏，试验终止。

由于位移与力的乘积是能量，即滞回曲线所围成的面积就是所消耗的能量，试验结构的能量耗散能力，以荷载-位移滞回曲线所包围的面积来衡量，即能量耗散因数。EBF-1能量耗散因数E1按式(1)计算：

(1)

得到：

采取同样的方法得到：

EBF-2能量耗散因数：

E2=1.28；

EBF-3能量耗散因数：

E3=0.89。

能量耗散因数E2较E1降低2.29%，E3较E1降低32.06%。因此，随耗能梁段长度的增加,K形偏心支撑钢框架的耗能能力下降。

2.3 骨架曲线对比

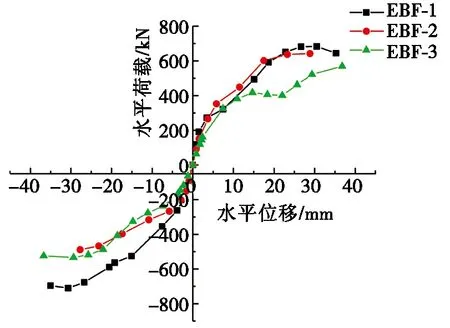
图7 骨架曲线对比图

图7为EBF-1、EBF-2、EBF-3骨架曲线对比图。由于构件加工、施工安装和螺栓预紧等各方面误差的存在，构件之间存在不同程度的缝隙，且在试验加载时，缝隙挤密压实，与耗能梁段和梁段之间相互错动，因此，3个试件的骨架曲线均有不同程度、不同时间点的抖动。

结构的塑性变形能力通过延性因数来度量。延性因数以试件破坏时所达到的极限位移值与相应试件的屈服位移值的比值计算，得到：

EBF-1延性因数：

μ1=9.54；

EBF-2延性因数：μ2=13.51；

EBF-3延性因数：μ3=10.01。

分析可知：EBF-2的延性因数较EBF-1的延性因数增加41.61%，EBF-3的延性因数较EBF-2的延性因数下降25.91%。说明耗能梁段长度的增加对提高偏心支撑钢框架延性性能具有一定的作用，如EBF-2的延性大于EBF-1的延性。但随着耗能梁段长度的再增加，偏心支撑钢框架的延性反而下降，如EBF-3的延性小于EBF-2的延性，由此可知，在EBF-1与EBF-3之间可能存在合适的耗能梁段长度，具有更加优越的延性性能，有待进一步研究。

2.4 刚度退化

结构的刚度对应为结构荷载曲线的切线刚度，定义为同级加载时，正反向荷载峰值绝对值与对应位移峰值绝对值之和的比值。

试件的刚度用割线刚度来表示，割线刚度Ki按式(2)计算得到：

(2)

其中：+Fi、-Fi为第i次正、反向峰值点的荷载值，kN；+Xi、-Xi为第i次正、反向峰值点的位移值，mm。

EBF-1初始刚度：

K1=81.32 kN/mm；

EBF-2初始刚度：

K2=71.20 kN/mm；

EBF-3初始刚度：

K3=54.00 kN/mm。

经测算表明：随着耗能梁段长度的增加，初始刚度降低，EBF-2的初始刚度较EBF-1降低12.44%，

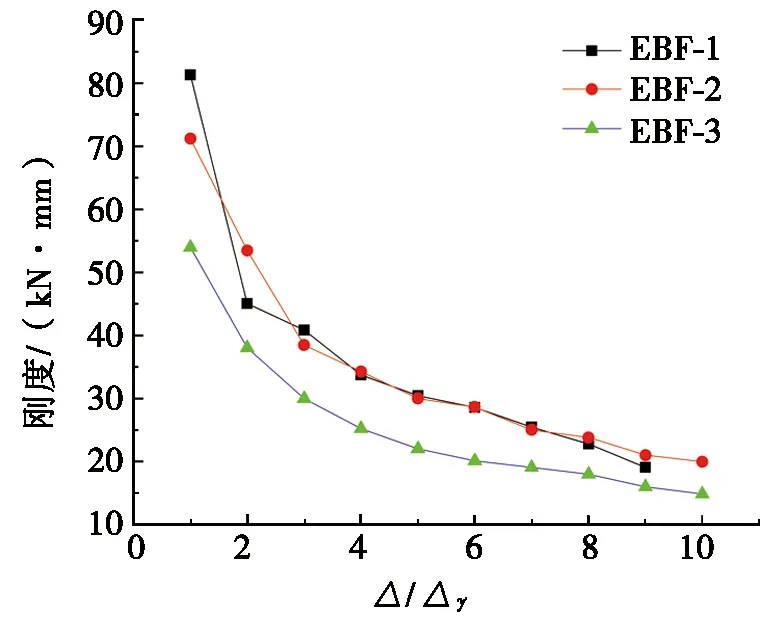
图8 钢框架刚度退化曲线对比

EBF-3的初始刚度较EBF-1降低33.60%，耗能梁段长度对偏心支撑钢框架的初始刚度产生明显影响。

把每级加载位移计算得到的割线刚度用曲线表示出来，即刚度退化曲线，图8为钢框架刚度退化曲线对比。图8中：△为加载过程中钢框架位移；△y为屈服位移。由图8可知：随着加载位移的增大，偏心支撑钢框架刚度均减小，EBF-1与EBF-2的刚度退化速度相当，EBF-3刚度退化速度快于EBF-1和EBF-2。由于耗能梁段与梁段之间的缝隙以及试验过程中螺栓孔等的挤压变形均会导致曲线不同程度的弯曲变形，3△y后刚度退化明显趋缓，承载力增长幅度较小。

3 结论

(1)耗能梁段长度对偏心支撑钢框架屈服荷载以及极限承载力产生明显影响。随耗能梁段长度的增加，偏心支撑钢框架屈服荷载降低，偏心支撑钢框架极限承载力降低。

(2)耗能梁段长度对偏心支撑钢框架耗散能力有影响。随耗能梁段长度的增加,K型偏心支撑钢框架的耗能能力下降。

(3)耗能梁段的长度对偏心支撑钢框架延性性能具有一定的影响，实际工程选择合适的耗能梁段长度对提高偏心支撑钢框架延性性能有很好的帮助。

(4)耗能梁段长度对偏心支撑钢框架的初始刚度产生明显影响，随着耗能梁段长度的增加，偏心支撑钢框架初始刚度降低。

(5)3种长度的偏心支撑钢框架，屈服、破坏均发生在耗能梁段，长度的改变没有影响整体偏心支撑钢框架的设计理念，即通过耗能梁段的非弹性变形来进行耗能，使得耗能梁段最先发生屈服，保护支撑斜杆不发生屈曲或者后发生屈曲，相应地延长结构抗震持续时间。耗能梁段的长度对偏心支撑钢框架的耗能性能和结构延性有着很大的影响，选择适当的耗能梁段长度，有助于提高偏心支撑钢框架的受力性能。