基于节点影响力的电力通信网拓扑结构诊断

刘 超

（国网南通供电公司，江苏 南通 226000）

0 引 言

在信息爆炸的时代，信息的真实性无从考量，需要借助网络诊断等能够保证系统稳定运行的技术手段分析网络信息的安全性，并找出其中隐藏的非观测信息。在网络传输过程中，网络诊断为其中的关键环节，对于可靠性的解读十分重要。为保证网络失效状态评判的准确性，需要重视网络诊断过程，降低不必要的损失。

1 网络节点的基本内涵

我国电力通信网具有复杂程度高的特点，不同地域位置具备不同的网络特征。在此种复杂结构的密切联系下形成了三角结构，从而出现了区域网络节点[1]。结合大量的技术资料可知，为避免网络崩溃，需要合理诊断网络拓扑结构，辨别融合网络中各要素的相互作用。网络节点具备中心性的特征，仅通过单一性能的方式判定网络节点影响力达不到分析和判定的要求，因此科学家们逐渐深入，给出多种诊断办法。例如，在删除节点后，观察生成树的具体数目，生成树的数量与节点影响力之间存在反比例的关系，即数量越大，影响效能越低。但在实际应用中容易出现均质化的情况，不利于准确分析节点影响力情况。因此，现阶段主要应用综合测算和核定的办法，基于节点接近度，判定领域的关键度，从而得出最终的节点影响力。运用此种方法的优势是，不仅能够缩短作用路径，而且能准确应用介数。此外，还可应用网络子图、随机游走以及节点收缩法测算影响力。

电力通信网是电力系统稳定运行的保障，其具备节点数量多和拓扑结构多变的优势，可提升网络的安全性。由于电力通信网节点失效将造成整个系统的失效，因此研究诊断网络拓扑结构十分必要。通过检查度中心性来判定节点影响力，可作用于电子邮件网络等结构中，提升三角结构运行的效能，保证路径转换的效用，发挥出末端节点的连通性[2]。

2 诊断网络拓扑结构所应用的理论

2.1 复杂网络模型

在网络拓扑诊断的过程中，需要准确分析鲁棒性和抗毁性，明确正常的工作状态，通过展示故障出现的位置，制定相应的维护意见，降低后期维护的成本[3]。对于网络节点影响力来说，二级节点度和节点度是确定其影响效能的基本要素，能够直观显示出状态变化对传播范围的影响，而三角结构作用于节点附近，应用聚类系数形成三角结构判定的结果。节点影响力的作用能力通过聚类系数得以体现，可真实反映传播影响的控制力。在实际研究中，为提升分析效能，一般删除节点容量等要素，保证网络结构内的节点均能具备同样的性能，形成无向无权的状态。一般通过以下几个公式得出节点度ki、节点二级度fi以及聚类系数ci，公式分别是：

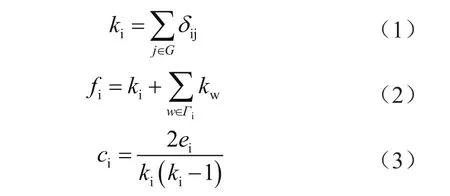
式中，ki表示节点i的度；fi表示网络节点的二级度，kw为节点w的度；Γi为节点i的邻居节点集合；ci为节点邻居间连通能力指标，即聚类系数；ei表示节点i邻居节点的连边数。式（1）中，从i到j已经连接时用1表示，没有连接时用0表示。利用以上3个式子可准确计算出无向网络中的多种因素。

2.2 多属性决策模型

此种模型可包含多个指标和属性，通过自带的筛选功能，挑选出可诊断网络拓扑结构运行状态的最优方案，属于属性权重确定的范围。采用多属性决策办法，依赖于相似关系定律，计算信息熵的数值，结合数据内容，确定最终的权重分配方式，保证各指标权重的数值[4]。对于属性值相似的指标来说，其相似度与节点能力间存在反比例关系，即相似度越小，节点能力越强。研究人员可通过此结果确定最终的解决方案，利用的计算公式是：

式中，Ej为网络属性信息熵的值；rij为第j个指标的第i个属性值；m是属性值的个数；n代表不同指标的数量；wj为第j个指标的权重。

2.3 节点影响力计算

节点影响力计算过程的完备性和精准程度将保证后期诊断的合理性。辨别不同节点所能够展现的形态，只有区分好影响力大小才能够精准设定维护措施，确定优先等级，从而提升电力通信网的运行效能。现阶段建立的网络结构的节点度集中在1或2，呈现无标度性且稀疏的特征，但不排除有些网络结构具备星型分布的特征。结合上述分析结果可知，在节点影响力的诊断过程中要先计算节点度，合理判定指标的影响效果，确保准确反映节点邻居模型运行状态，保持良好的属性特征。上文提到了聚类系数这一概念，此要素主要作用是真实反映出三角结构的运行情况，对于衡量邻居紧密程度起到一定的作用。节点影响力的计算方法还可利用路径判断的方式实现业务传输，下文将给出一种评价方式，其应用的公式是：

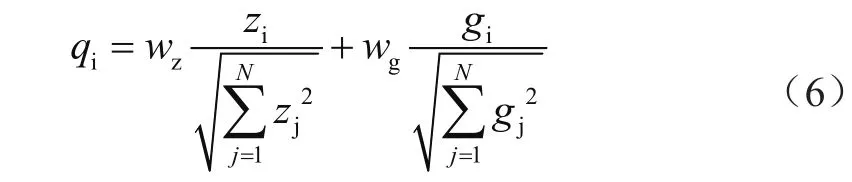
式中，qi为引出的节点影响力评价指标；wz和wg为多属性决策模型确定的权值。zi为节点度ki归一化的结果，gi是参数。

聚类系数和节点度所指向的基本要素不同，即侧重点不同。因而需要利用同趋化函数处理两个指标数值，得出性能相互作用产生的实际效果，保证同一节点的情况得以准确反馈。利用测试算法可构建如图1所示的节点网络拓扑图，结合该图进行分析，得出表1所示的属性值，根据表中具体数据可以看出，节点不同，其影响力不相同，仅通过判别指标度无法准确得到节点影响力大小的具体数值，进而无法量化影响力。

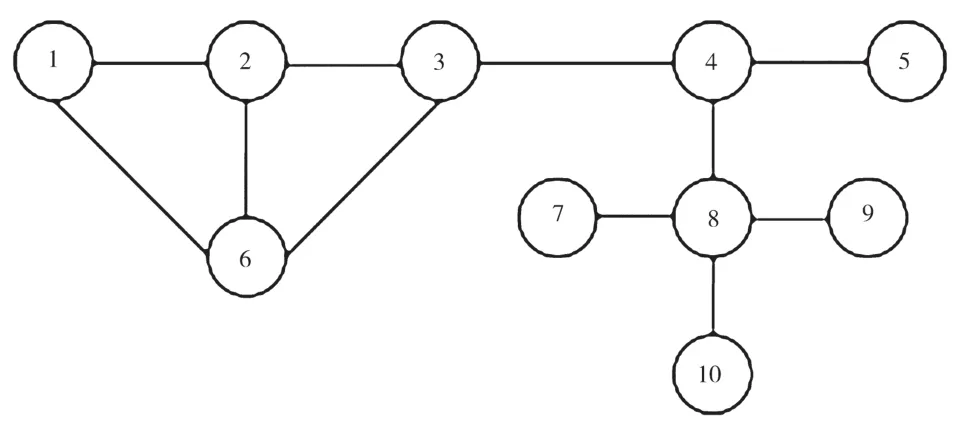
图1 10节点网络拓扑图

通过分析表1内容可知，在衡量节点影响度的过程中，要同时考虑规模属性和聚集特点，区分两种属性的具体作用，确保结果的准确性。

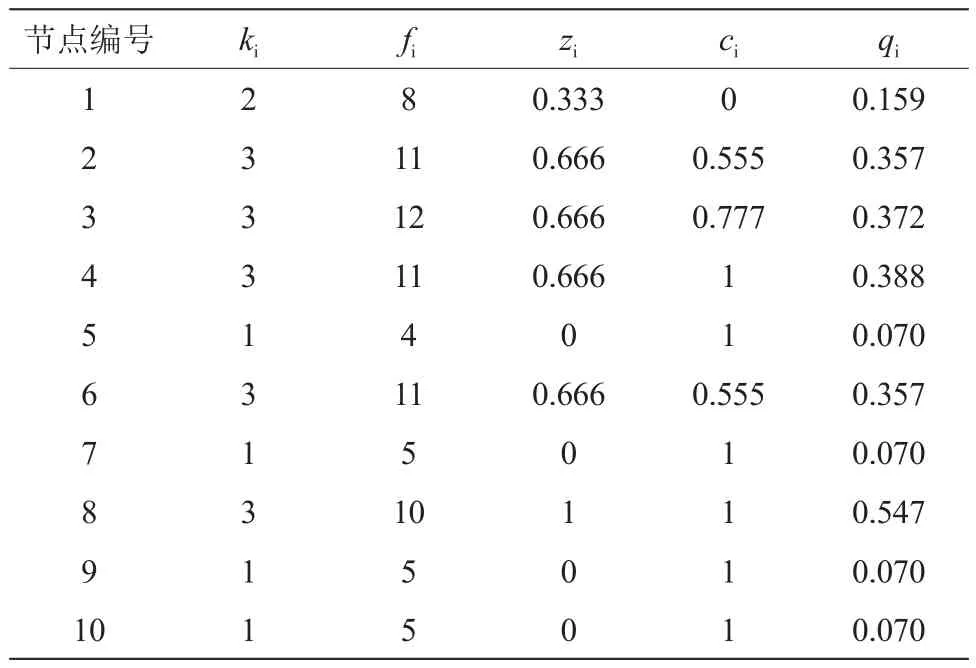
表1 网络中节点的属性

2.4 诊断分析

网络诊断的主要依据是拓扑可靠性，结合上文的有关内容可知，不同的节点对于整体结构的影响效果存在差别，而进行删除节点的操作要分析下降程度，针对可靠性等因素分析影响作用的效果，保证最终结果精准度。不同的拓扑结构所显示的下降程度有所区别，基于节点相似性的特征，找准算法，获取准确的影响力效果，提升网络监管的实际效应。在实际分析过程中，需要从鲁棒性和抗毁性两个角度分析，做出正确的判断[6]。

2.4.1 鲁棒性

删除节点后网络连通属性由鲁棒性来体现，作用范围可覆盖各个单元，表彰在节点删除操作后各机构的基本属性。从中获取到薄弱单元和结构，定量描述相应的单元属性，其中使用节点对数和总节点对数之比的均值确定移除后各单元的具体情况。应用公式为：

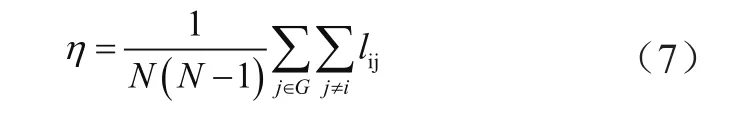
若得到的η值减小，说明网络系统中不能够准确连接的节点对数增加，应当找到解决裂解问题的办法，降低影响效果。

2.4.2 抗损性

抗损性能够反应出关键部位抵御攻击的能力，通过性能的角度准确核定电力通信网络的作用效能，保证关键服务的能力得以准确展现，从而定量描述网络性能。抗损性越强，说明该网络系统能够抵御更为强劲的攻击，其基本性能可满足高效应用的要求。在进行节点删除作业时，可明确作用较强的节点位置，通过查看网络效率即可准确获取到节点的作用能力，提升对抗损性的认识程度。信息在距离较近的节点之间更容易传播，自然工作效率可得到一定的提升。在计算网络效率的环节，利用节点最短距离的倒数可直接反映节点的效率。节点删除后的效率有两种可能的变化情况，一种是节点删除后效率提升，此种情况需要满足在原节点相连的结构中存在中间节点。由于节点删除，其相连接的线路被切断，因此线路重新组合，缩短了其中的运行路径，提升整体运行的效率。另一种情况是整个网络效率为0，此时原连接线路中不存在中间节点，删除节点则剪断了连通的线路，导致没有可作用的线路结构，形成0效率网络。在具体计算中应当计算效率平均值，找准节点个数和删除节点所构成的点集合，若最终结果稳定在[0，1]之间，说明计算准确，并且网络最佳状态是全局网络效益E=1。而当E=0时，说明没有形成连通的网络，各个点独立存在[7]。

3 仿真分析

3.1 网络结构

为提升网络结构稳定性和安全性研究的深度，可应用仿真分析的方式，准确分析仿真和真实网络之间的诊断结果。不同区域的的通信网结构具备不同的特性，省级网络具有小世界的特点，市级网络结构具备无标度的特性，基于以上特性分析结果，选用1 000节点的小世界仿真分析省级网络，市级网络则需要应用100节点予以测算。经过大量的试验和数据分析后得出表2所示的结果。其中准确展现节点平均度M、网络节点数N、最短距离d、聚类系数ci以及边数k对于整体网络运行的作用效果[8]。

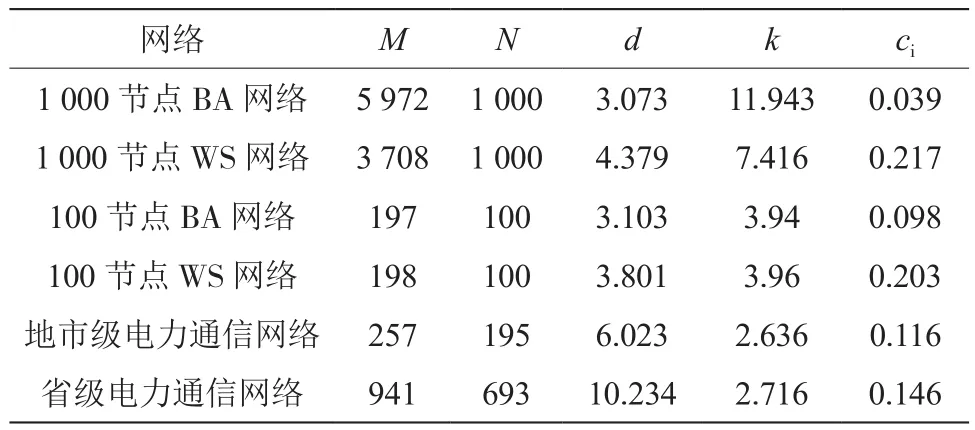
表2 不同仿真网络的特征参数

3.2 仿真网络诊断

3.2.1 结构特征

结合不同的网络基本结构分析可知，在诊断网络效率环节，分别利用边数和参数不同的网络结构总结出，在仿真网络结构中，想要获得最佳结果需要利用9种无标度网络，求出作用的平均区间，准确设定平均距离，将平均聚类系数控制在一定的区间范围内。本文主要通过确定边数的小世界网络和平均参数为4的模拟网络仿真电力通信网结构。但由于节点边数的影响效果与实际网络存在差距，真实性有待控制，因此要合理处理仿真误差。

3.2.2 抗损性诊断

抗损性诊断基于多项指标，通过分析二级节点度、节点度以及集聚系数等指标，对不同的网络采用不同的排序方式。一般在相同的网络结构中，将排名位于前端的节点删除。不同网络结构在分析删除节点后的网络效率时，要从小世界和无标度所具有的特点出发计算下降率，进而得出抗损性的变化情况。分析仿真网络下降率变化情况的图表内容，发现经过上述操作后，下降率的值随着m的增大而减小，说明影响力逐渐降低，具备更强的抗损性能。即使其他指标呈现下降的趋势，但还可以根据qi值衡量网络抗损性。而在WS网络中，观察到平均度增大可提升抗损性[9]。

3.2.3 鲁棒性诊断

鲁棒性诊断采用删除不同指标的办法，准确计算节点受到的影响作用，观察标准是连通度。结合连通度的变化衡量各项指标的影响效果。本文选用删除前5个节点的办法，观察指标出现的分歧，最终按照相应的顺序展开对鲁棒性的讨论。结合具体数值可知，选用多个节点删除后，网络整体效率并无明显变化，出现此种情况的原因是仿真网络边数足够多，删除几个节点并不能影响最短距离的数值，因此连通性并没有波动性的变化。说明在实际测算中，需要逐个删除节点，观察在删除第几个节点后会带来的较大差异，从而确定网络连通特性。

3.3 真实网络诊断

3.3.1 抗损性诊断

抗损性诊断在真实网络结构中同样要选定多个指标，适当删除排名在[10%，30%]的节点，关注下降率的变化，分析影响效果。结合城市网络测算图可知，网络下降率与节点删除的比例存在关系，当比例上升时，效率也随之提升，可以得出节点删除的数量与抗损性能之间存在反比关系，对于不同级别的网络结构来讲有着相通的结论。

3.3.2 鲁棒性诊断

鲁棒性诊断不同级别的网络呈现出不同的作用效果，对于地市级的网络结构来说，仅删除几个节点就观察到不同的指标变化情况不统一，经过多次实验并结合仿真过程分析出节点12号对网络性能的影响效果最强，其周围不具备较多的邻边，呈现全网的最大度数，因此节点影响力qi值对于鲁棒性的诊断有着直接的作用。在分析省级网络时，同样出现对应的结果。

4 结 论

综上所述，节点影响力qi值对于诊断网络拓扑结构运行效果起到直接的作用，在确定鲁棒性和抗损性的阶段要深度研究节点删除对于整体网络的影响效果，从而保证网络使用的安全性。在后续的工作和研究中，要加强对级联失效判断节点影响效果的力度，重视小概率事件。