中低速磁浮车辆道岔区设备限界研究

李经伟

(中铁第四勘察设计院集团有限公司 湖北武汉 430063)

1 概述

中低速磁浮交通具有环保、安全性高、爬坡能力强、转弯半径小、能耗低、运行噪声小、中低运量等优点，作为地铁主干网的有益补充，越来越受到青睐，目前已有数个城市已建或在建中低速磁浮工程。限界设计是磁浮工程建设中的重要一环，决定着工程的经济性和安全性[1]。

目前在中低速磁浮领域，对车辆限界及正线区间上的设备限界、建筑限界研究已较为成熟[2-3]，但对道岔区的限界研究尚属空白。道岔区设备限界直接决定了道岔区的轨旁设备安装位置及土建结构尺寸，对道岔区设备限界的明确，可有效保障车辆运行安全并节约工程投资。因此，本文以长沙磁浮快线工程为例，对中低速磁浮车辆在道岔区的设备限界进行探讨，以期为今后中低速磁浮道岔区的限界设计提供借鉴。

2 中低速磁浮车辆道岔区限界计算计及因素分析

中低速磁浮道岔是列车换线设备，可实现列车到发、会让、检修等作业。由于磁浮列车采用抱轨走行方式，道岔必须采用移梁实现换轨，其类型可分为单开道岔、三开道岔、单渡线道岔及交叉渡线4种[4]。

磁浮道岔采用三段定心式结构，主要由垛梁、一段主动梁、两段从动梁以及安装于梁上的F轨组成，主梁和从动梁都有一个转动中心[5]。道岔转辙到位后，由锁定系统锁定于地面锁销座上，从而保证列车安全通过。单开道岔基本参数见表1，单开道岔总体布置见图1[6-7]。

图1 单开道岔布置

表1 单开道岔基本参数

普通轮轨地铁车辆在道岔区限界计算因素应包含:(1)在直线地段的车辆及设备限界；(2)在道岔区的几何偏移量；(3)在道岔区的动态偏移量；(4)轨距加宽量；(5)轨距弹性挤开量[8-9]。

在中低速磁浮工程的限界设计工作中，由于道岔结构复杂及其特殊性，限界计算需要在完成了直线地段车辆及设备限界的制定后，再根据不同的车辆参数和道岔类型计算出岔区限界加宽量，并合成后形成道岔区限界。

中低速磁浮车辆道岔区的限界计算需计及的因素，应分析直线地段车辆及设备限界的计及因素，并结合中低速磁浮车辆和轨道线路的特点考虑其它因素[10-12]。

中低速磁浮车辆限界是磁浮车辆以正常工况在平直线路上运行所形成的最大动态包络线，是综合考虑车辆各部件横向、垂向偏移后的动态轨迹。车辆限界计算所计及的因素主要包括车辆、轨道线路、外部环境三个方面。

中低速磁浮车辆在直线地段的设备限界是在车辆限界基础上增加安全间隙后形成，安全间隙主要包含车辆的故障工况，见表2。

表2 中低速磁浮车辆限界计算计及因素

磁浮车辆设置了横向滑橇来约束悬浮架的横向位移，限制了悬浮架的较大偏移量，所以当模块横向位移大于横向滑橇与F轨间的几何极限间隙时，将与F轨接触，从而限制悬浮架的进一步横移。垂向位移上，由于悬浮架在向上的偏移量上受到F轨的磁极面约束，向下的偏移量受到F轨滑橇接触面约束，车辆垂向位移幅度受限，这在车辆限界和直线段设备限界的横向和垂向偏移量计算中已经考虑。因此由超高和欠超高而引起的车体不平衡动态偏移量不予考虑。

同时，对比轮轨地铁车辆，中低速磁浮车辆限界已计及F轨的垂向和横向变形及偏差，且F轨不存在轨距加宽，因此轨距加宽量及轨距弹性挤开量都可不予考虑。

综上，可得出中低速磁浮车辆在道岔区的设备限界计算计及因素应包含:车辆在直线地段的设备限界＋在道岔区的几何偏移量。

3 道岔区设备限界计算

中低速磁浮道岔有四种形式，因基本参数一致，本文以单开道岔为对象进行计算，其它道岔形式可对计算结果进行组合使用。

3.1 模型建立

中低速磁浮道岔(见图2)主动梁和两段从动梁转向侧向后，形成了三段折线结构，从岔心开始三段折角依次为 2.3°、4.6°、6.9°。

图2 道岔结构示意(单位:mm)

中低速磁浮车辆的悬浮架与车体通过滑台连接，当车辆通过道岔折线时，第2、5位固定滑台横向与车体固定连接，因此第2、5位左右滑台连线的中心始终在车体中心线上，并位于道岔折线上，实际上构成了5个悬浮架模块过道岔折线时车体的转动中心。

车辆在道岔上运动时，可假定车辆是个刚性体。车辆纵向中心线是直线，而道岔的轨道中心是折线。车辆中心线不随轨道而改变形状，导致车辆端部和中部偏离轨道中心线，因而在折线的内、外侧就产生了几何加宽量。

本文分别采用窄体模型和宽体模型两种计算方法，进行道岔区设备限界的计算。

方法一:窄体模型计算法

在曲线段或者道岔区计算车辆设备限界时，将车辆简化为一条与车体同长的直线，以此为基础计算曲线或者道岔区的几何加宽量，再加上车辆直线地段的设备限界，可得到车辆在道岔区的设备限界，原理(道岔区折线地段可类比于曲线地段)见图3。

图3 窄体模型几何加宽量计算

方法二:宽体模型计算法

以直线地段的车辆设备限界为基础，进行道岔区的车辆运行模拟。将车辆简化为一个与车辆同长、与直线段设备限界同宽的矩形，以此为基础进行模拟计算，可直接得到道岔区的车辆设备限界，原理见图4。

图4 宽体模型几何加宽量计算

两种方法的区别在于车辆简化模型不同，本文对上述两种计算方法分别进行研究，并进行结果对比。

取长沙中低速磁浮工程中磁浮车辆MB型车头车为例，其参数见表3。

表3 车辆基本参数 mm

方法一(窄体模型计算法)车辆模型见图5。A、B为悬浮架2、5滑台的中心点；B端为车头端；O′为AB的中点。

图5 车辆窄体模型(单位:mm)

方法二(宽体模型计算法)车辆模型见图6。A、B为悬浮架2、5滑台的中心点；O′为AB的中点；C为车体端头轨道外侧点；D为车体轨道内侧中点。

根据直线段设备限界计算公式，可得其设备限界最宽点为1 497 mm，选取具有代表性的头车作为案例，车辆模型可简化如下:

图6 车辆宽体模型(单位:mm)

3.2 计算方法

本文采用MATLAB软件，对上述所建立的模型分别进行数学建模并求解，同时模拟出车辆运动图形，既可以反映数学计算的精确性，也可以反映车辆运行动态的直观性。

(1)模型简化

定义坐标系O′点为原点，简化单开道岔模型，分为一段主动梁、两段从动梁和主轨道四段，分别为Q0-Q1、Q1-Q2、Q2-Q3、Q3-Q4。

(2)计算主动梁、两段从动梁及主轨道的斜率

(3)分析列车在道岔上位置关系

悬浮架上的A、B两点一直在轨道上，本文主要分析悬浮架上的 A、B 两点和Q0、Q1、Q2、Q3、Q4位置关系。

根据A、B 两点与四段直线转折点Q0、Q1、Q2、Q3、Q4位置关系分段求解，分为以下7段过程:

①B——Q0Q1，A——Q0Q1；

②B——Q1Q2，A——Q0Q1；

③B——Q2Q3，A——Q0Q1；

④B——Q2Q3，A——Q1Q2；

⑤B——Q3Q4，A——Q1Q2；

⑥B——Q3Q4，A——Q2Q3；

⑦B——Q3Q4，A——Q3Q4。

(4)计算过程

①以B点横坐标为自变量，从最开始横坐标和Q0(-28 472，-2 900)相同，到最终A点经过Q4(2 000，0)停止，取步长500 mm。

②通过B所在直线方程求解B横坐标，再利用A所在直线方程和AB定长(LAB＝8 400)，联立可求A横纵坐标。

③通过 A、B 坐标求 O′点坐标(XO′，YO′)和 AB斜率

④利用O′点坐标和夹角α求C点和D点坐标

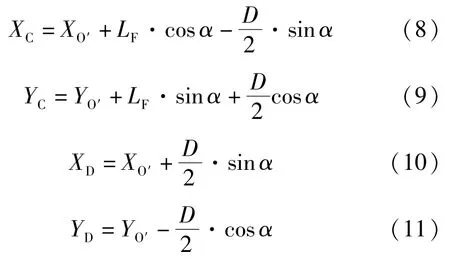
其中，α为AB与X轴夹角。

3.3 计算结果

采用Matlab运行模拟后，两种简化模型模拟结果见图7。其中窄体模型反映的是限界加宽量，宽体模型反映的是车体动态轮廓。

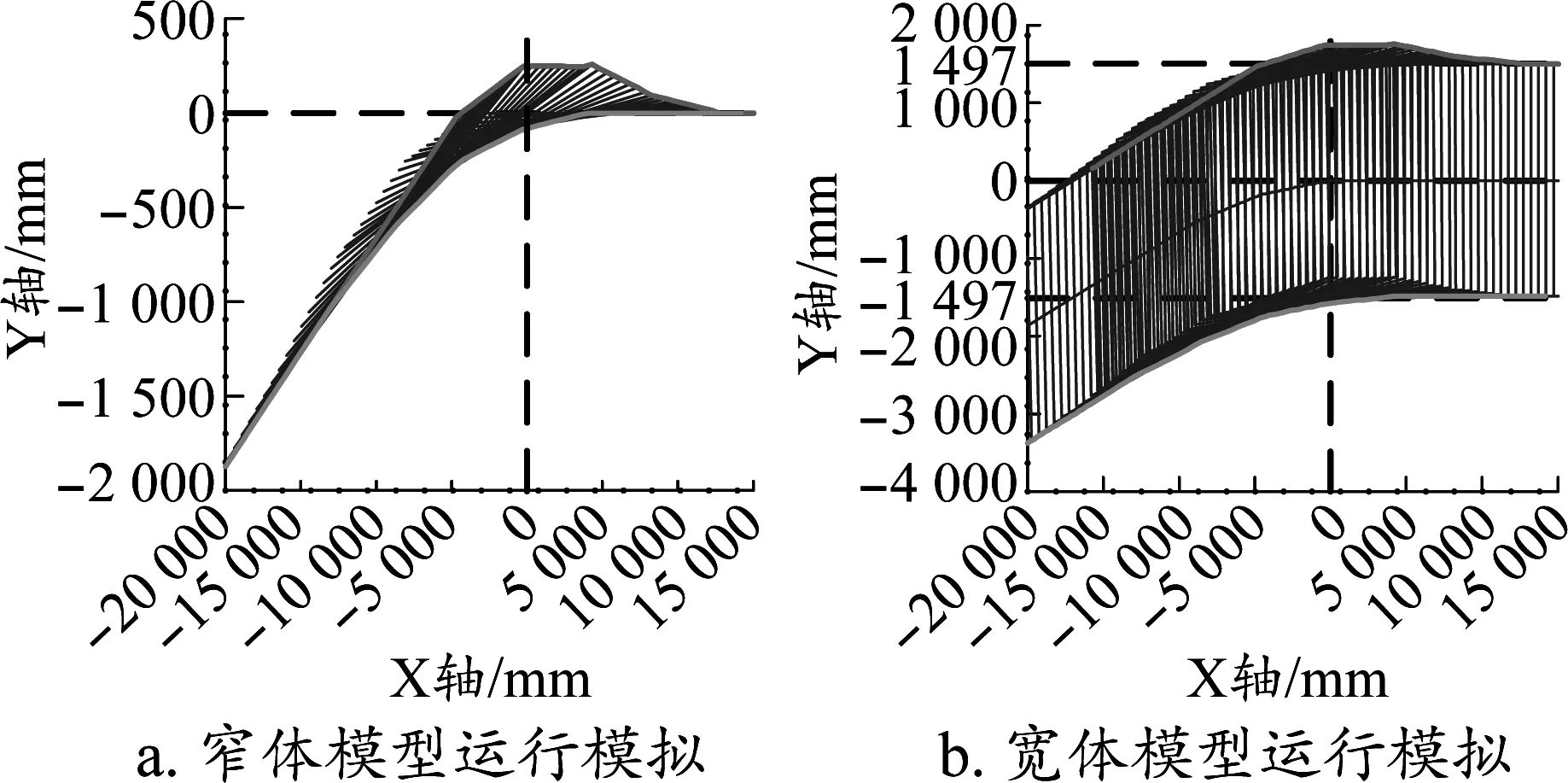
图7 两种模型运行仿真

对窄体模型每个点数据加直线地段设备限界最大值(1 497 mm)处理后，叠加取最外侧点轮廓并连线，可得两种模型在道岔区设备限界坐标，见图8。

3.4 计算结果比对

由图8可知，当车辆处于道岔侧股主梁处，斜率最大，两种计算方法的差别最大，为10.84 mm，窄体模型的计算值大于宽体模型；当车辆到达直轨处，即斜率为0时，两种计算方法的差别为0。经分析，主要是因为车辆本身具有宽度，处于道岔侧股主梁处时，道岔斜率引起的加宽量与设备限界引起的加宽量不在同一个方向，不应是简单地数值相加。而采用宽体模型计算法可避免以上问题。

分析宽体模型的计算结果，可得出中低速磁浮MB型车在道岔外侧的加宽值，自岔前12.7 m处起至岔后4.2 m处有加宽，其中最大加宽处位于岔前4.5 m处，最大加宽量为255 mm。其计算外轮廓坐标值见表4。

表4 MB车道岔区运行外轮廓坐标值

4 结论

通过对中低速磁浮车辆限界和设备限界的计算方法进行分析，结合磁浮车辆及道岔结构特点，可得出结论，即中低速磁浮车辆道岔区设备限界仅需考虑车辆在直线地段的设备限界和车辆在道岔区的几何偏移量。通过对窄体模型和宽体模型两种模型模拟运行计算结果进行对比，可知宽体模型的计算结果更为合理，并采用宽体模型法计算出磁浮MB型车在道岔区的运行坐标，可供后期工程设计参考。