基于K-L变换和奇异值分解的人脸识别

王银花

(1.铜陵学院 电气工程学院，安徽省铜陵市翠湖四路1335号 244000；2.光电子应用安徽省工程技术研究中心，安徽省铜陵市翠湖四路1335号 244000)

人脸识别是利用计算机分析人脸图像信息的过程。这种分析过程是采用相关方法，利用计算机完成在复杂的图像场景中检测出所需要的特征人脸信息，并智能匹配识别正确图象。

人脸识别技术广泛运用于多种场景，公安系统中可用于罪犯分子的身份识别；在银行、证券、网络购物和借贷等实名制和安全性要求较高的领域，可作为用户远程注册和密码找回环节中的辅助验证；日常生活中使用人脸识别作为门禁系统的解锁方式，可方便实现无需携带任何物件的验证流程；在公司单位以及学校的考勤系统中使用人脸识别进行考勤方便快捷、成本较低，并且可以有效防止代打卡的不良现象，因此特别适合群体的大规模流动性较高的考勤场景。[1]

K-L变换又称霍特林(Hotelling)变换或者主成分分析，它属于均方差意义下的最佳变换，其突出优点是相关性非常好，得到的主成分是互相线性不相关的。K-L变换的基本原理就是用较少数量的特征对样本进行描述，以达到降低特征空间维数。与K-L变换相结合的是很多算法适用于解决多种图像处理问题，如人脸识别、图像压缩和信号传输等。

计算机中的图像是以高维的空间形式存储的。用离散K-L变换对人脸图像的原始高维的空间向量进行转换，构造出人脸图像数据集的协方差矩阵，再对协方差矩阵进行正交变换，求出其特征向量。数据集的特征值利用奇异值分解(singular value decomposition，SVD)中的奇异值来表征，把特征值按照重要性原则进行重新排列，降维的过程就是舍弃不重要的特征向量，将剩下的特征向量组成的空间构成降维后的新空间。在人脸图像中每个不同类别的图像变量对应一个向量，每组特征向量构成特征的一个集合，这个集合代表一个人脸图像信息，也称为“特征脸”图像。

1 基本原理

1.1 K-L变换基本原理

K-L变换的目的就是对原始向量进行正交变换，以组成新的向量。该新向量的特征数比较少，并且各特征间不相关。下面讲述怎样找到合适的变换矩阵。

将向量X在某一种空间坐标系统中的描述，转换成用另一种基向量组成的坐标空间来表示。这组基向量是正交的，其中每个坐标基向量用øj(j=1,2,…，∞)表示。向量X可表示成：

(1)

取基向量为正交向量，即：

(2)

由于øj是确定性向量，因此均方误差可改写为：

令Ψ=E[XXT]

用拉格朗日乘子法，可以求出在满足正交条件下，取ε极值的坐标系统，即用函数

对øj(j=1,2,…，∞)求导数，因此有：

(Ψ-λjI)øj=0j=d+1,…,∞

λj是矩阵Ψ的特征值，将特征值按从大到小顺序排列，得λ1≥λ2≥…≥λd≥…，此时取前d项特征值对应的特征向量组成新的坐标系。在这种情况下可使向量的均方误差为最小。此时截断误差为：

满足上述条件所做的矩阵变换就称为K-L变换。

在一个一般的图像中，每个像素点与其相邻像素点之间都会呈现出很高的相关性。K-L变换是一维变换，在对图像信号进行变换时，矢量可以是一幅图像或一幅图像中的子图像。矢量各分量之间的相关性反映了像素之间的相关性。为了得到一幅图像的矢量表示，可以将图像或子图像的像素值按行行相连或列列相连的次序排列。

假设人脸图像库中有K幅人脸图像，用列向量或行向量表示为X1,X2,…,XK，每个向量的维数是N。其人脸平均图像：

(3)

由此可得到每幅图像的均差：

(4)

这样可计算协方差矩阵：

(5)

式(5)中的协方差矩阵的大小是N2×N2，直接求该矩阵的特征值和对应的正交归一的特征向量是相当困难的，即使对尺寸较小的图像这个计算量也是很大的。为了降低运算量，提高图像识别的速度，现将每幅图像的均差形成一个新的矩阵：

(6)

则式(5)可以写成：

(7)

式(7)中的协方差矩阵的大小是N×N。根据线性代数理论，式(5)和式(7)相比较实现了协方差矩阵的特征值和对应的特征向量的转化计算，减少了计算量。这在处理图像这样规模较大的矩阵时是非常有意义的。

1.2 奇异值分解

奇异值分解(SVD)在线性代数中是一种非常重要的矩阵分解方式，它是特征分解在任意矩阵上的扩充。SVD在信号处理、模式识别、统计学等领域都有重要应用。该方法的基本原理就是借助求解较低维数矩阵的特征值和特征向量以达到间接计算出较高维数矩阵的特征向量。[2]在人脸识别中这些较低维数的特征向量就构成识别对比的“特征脸”信息。采用这种计算方式大大降低了计算量。

设A是一秩为r的n×r维矩阵，则存在两个正交矩阵

U=[u1,u2,…,ur]∈Rn×rUTU=I

V=[v1,v2,…,vr]∈Rn×rVTV=I

以及对角阵：

Λ=diag[λ1,λ2,…,λr]∈Rn×r

λi(i=1,2,…,r)是矩阵AAT和AT的非零特征值，且对角阵中的特征值按降序排列。

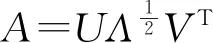
易知

(8)

由式(8)计算的特征向量个数为M，它比N2小很多。人脸识别时的ui也即图像的特征向量，它利用变换把原始高维矩阵转换成较低维矩阵，从而间接求出原始矩阵的特征值以及对应的特征向量。[3]

1.3 选取特征向量

通过K-L变换，可以将原始人脸图像数据降维。根据应用的需要，并非所有的特征向量都有很大的保留意义。进一步可以在原始数据对应的协方差矩阵的多个奇异值中，只保留最大的前几个奇异值所对应的特征向量作为线性变换矩阵，这样做可以实现进一步的降维。考虑到使用变换作为对人脸图像的压缩手段，采用SVD分解图像保留最大部分的奇异值，就可以在压缩图像数据的同时，还能最大化减少图像信息的损失。

可以选取最大的前k个特征向量，k的选取满足：

(9)

比如α=90%当选取，就是保留的图像样本数据前k个特征向量，他们的能量占整个能量的90%以上。

1.4 产生矩阵的选取

在考虑到训练样本的类别信息，以及节省计算量的要求，采用训练样本集的类间散布矩阵作为K-L变换的产生矩阵。

把每个人的训练样本的均值图像失量向由“特征脸”图像矢量所展成的子空间上进行投影，由此得到的坐标系数向量就是其K-L变换的展开系数向量，即：

ci=UTμii=1,2,…,P

(10)

式(10)中P为人脸识别训练样本集包含的总人数，μi为训练样本集中第i个人的平均图像向量。由此可得：

(11)

其中C=[c1,c2,…,cp]，ci为训练样本集中第i个人的特征系数向量。

全部样本的散点矩阵描述为：

采用线性变换对特征降维结果进行描述为：

Wopt=argmax|WTS*W|=[ω1,ω2,…，ωk]

(12)

式中，{wi|i=1,2,…,m}表示是原始特征空间的k个特征系数向量，以此构成人脸图像识别中的“特征脸”信息。

1.5 欧氏距离

欧氏距离是一个普遍被采用的距离定义。m维空间中两点之间的实际距离，即是求两点间向量的自然长度，即点到原点的距离。在三维空间以及二维空间中的欧氏距离就是空间两点之间的实际距离。将欧氏距离看作信号的相似程度，距离越短说明信号越相似。欧式距离的计算公式为

将欧氏距离的分类表示如下。

(1)二维平面上两点的欧式距离

令两点坐标分别为A(x1,y1)，B(x2,y2)。

(2)三维空间平面上两点的欧式距离

令两点坐标分别为A(x1,y1,z1)，B(x2,y2,z2)。

(3)两个n维向量上两点的欧式距离。令两点坐标分别为A(x11,x12,…,x1n)，B(x21,x22,…,x2n)。

两幅图像之间的距离反映了图像的相似性，距离越近，图像的相似度越高[4]。欧氏距离变换在数字图像处理中有着广泛的应用。将图像欧氏距离应用于传统人脸识别算法，能提高人脸识别算法的效率[5]。

在人脸识别系统中，设有H个类别的训练样本。每类样本有L个参数，第i类样本可表示为Xi=(Xi1,Xi2,…XiL)。对于任意测试样本X=(X1,X2,…,XL)由下式计算其欧式距离:

(13)

比较X到各类的距离，若满足:

dj(X,Xj)

人脸分类识别器就是选择最小的欧氏距离作为最佳匹配的人脸的过程。[6]采用欧式距离法循环计算测试样本与训练集里每类样本的距离，最终找出与测试样本最近的训练集中的已知类别，并将其作为判别输出。

1.6 人脸识别率

用欧氏距离法求出与其最相近的一个图像，识别为该类。所有测试集识别完后，最后求出识别率。用Nright和Ntest分别表示正确识别的人脸数和人脸总数。人脸识别率定义为：

(14)

2 人脸识别流程

人脸识别的主要方案是获得待识别图像相对于训练集平均人脸的差分图像，然后在特征人脸空间中获得图像的坐标。最后，利用欧氏距离法对图像进行识别归类。具体人脸识别系统的运行由以下5个步骤完成。

步骤1：搜集人脸图像，将库里的多张照片分成两组。一组作为训练库，一组作为测试库。读取训练集下指定个数的图像，将人脸的像素保存到到一个二维数组中，将该数组按列排成列向量，即每一列表示一张图像的像素信息。

步骤2：选定产生矩阵，分别选取每个人的n幅脸图像作为训练样本集，进行K-L变换，利用奇异值分解计算出相应的特征向量。计算出每个人训练样本的平均图像向量。确定式(9)中的α，选取出“特征脸”向量。

步骤3：选取测试库中的人脸图像进行测试，分别计算出它们在特征脸空间中的坐标系数向量，即特征系数向量。

步骤4：分别计算测试样本特征系数向量与每个人训练样本特征系数向量的欧氏距离，选取距离最小的样本类别作为识别结果，并与测试样本本身所属于的类别比较，判断识别的正误。

步骤5：统计正确的次数，求出人脸图像识别率。

3 实验结果及分析

文中采用Matlab2017b仿真软件作为工具平台，实验以剑桥大学AT&T实验室创建的ORL(Olivetti Research Laboratory)人脸数据库作为人脸图像识别实验对象。ORL人脸库是由英国剑桥Olivetti实验室从1992年4月至1994年4月期间拍摄的一系列人脸图像组成的，共有40个不同年龄、不同性别和不同种族的采集对象。每个对象10幅图像共计400幅灰度图像组成，图像尺寸是92×112，图像背景为黑色。其中人脸部分表情和细节均有变化，例如笑与不笑、眼睛睁着或闭着，戴或不戴眼镜等，人脸姿态也有变化，其深度旋转和平面旋转可达20度，该库是目前使用最广泛的标准数据库，它含有大量的比较结果。其中部分人脸图像分别如图1和图2所示。

图1 第20位采集对象的其中4副图像的细节展示Fig.1 Detail display of 4 images of the 20th acquisition object

图2 不同采集对象的图像显示Fig.2 Image display of different acquisition objects

选取前n张人脸图像作为训练样本，后10-n张人脸图像作为测试样本。根据本文所示方法，得到训练样本的过程中生成的特征向量，它是从高维矢量空间的人脸图像的协方差矩阵计算而来。通过保留那些具有较大特征值的特征向量的方法得到人脸分类识别时所需要的“特征脸”信息，该方法相比其他手段在效率方面比较有优势，短时间就可以处理大量人脸识别。仿真实验中的一些特征脸如图3所示。

图3 部分特征脸图像Fig.3 Some feature face images

测试样本集中随机选取的20个不同人脸图像，选定类间散布矩阵为产生矩阵，分别选取每个人的n(n<10)幅脸图像作为训练样本集，为了降低维数，选择取值最大的前90%的特征值保留。对图像进行K-L变换，利用奇异值分解计算出相应的特征向量，形成“特征脸”向量，记录不同的n采用本文方法得到人脸识别正确率如表1所示。由表1可知测试样本集的识别正确率随着训练样本中的每个人的人脸图片数的增加而增大。

表1 人脸识别正确率(α=90%)Tab.1 The accuracy of face recognition(α=90%)

选取训练样本集为所有人的第1至7幅脸图像，选取不同的，计算选取出“特征脸”向量，记录不同的采用本文方法得到是人脸识别正确率如表2所示。由表2可知测试样本集的识别正确率在一定范围内随着值的增大而增大。

表2 不同的α值对人脸识别正确率的影响(n=7)Tab.2 Influence of different values of α on face recognition accuracy(n=7)

仿真实验过程中的部分待识别图像及其对应识别结果如图4所示。

图4 部分待识别图像及其对应识别结果Fig.4 Part of the image to be recognized and its corresponding recognition results

4 结束语

人脸识别是计算机视觉和模式识别领域的一个活跃课题,有着十分广泛的应用前景。文中采用K-L变换、奇异值分解分析技术对人脸图像中信息量少的特征进行抑制，有效降低特征的维数，得到包含人脸原始信息的主要成分特征，形成“特征脸”向量。以欧氏距离法作为识别分类器，使用Matlab作为工具平台,进行人脸识别实验，根据多次仿真测试结果可以看出使用该方法能够取得较为满意的人脸识别结果。